类岩石材料脆性特征与配合比方案试验研究
郭 义 李昕昊 王创业 韩天宇 游 茹 于 波
(1.内蒙古科技大学矿业与煤炭学院,内蒙古 包头 014010;2.陕西宇佳投资置业有限公司羊场煤矿,内蒙古 鄂尔多斯 017000)
目前,在各类岩石工程中,天然岩石的力学性质研究备受研究人员的重视,然而,伴随着矿山开采的深部化,深部高地应力、高温等复杂环境致使原岩取样较为困难。类岩石材料具备原料成本低廉、制作简单、试验条件和方案便于调节等优点,而类岩石材料可在一定程度上反映岩石的破坏特点,因此类岩石材料在岩石工程室内试验方面得到了广泛研究。王汉鹏等[1]通过铁精粉、重晶石粉、石英砂为骨料,松香、酒精、石膏为胶结剂研制出相对理想的新型地质模型相似材料;林海飞等[2]通过正交试验设计类岩石材料配比并对其进行线性回归分析以确认配比可靠性;申艳军等[3]制备了类砂岩材料并探究了各材料对类砂岩物理及力学性质的影响;史小萌等[4]通过以水泥和石膏确定相似材料配比并通过工程应用确定其配比的可靠性;袁璞等[5]以砂为骨料、水泥石膏为胶结剂,通过单轴压缩试验研究养护时间对类岩石抗压性能的影响,得到合理的养护时间;Gu等[6]对脆性岩石材料进行模型试验,得出水泥含量对裂缝的扩展及其力学特性有很大的影响;Yang等[7]以石英砂和水泥为类岩石材料,模拟砾岩力学性能,并采用极差分析法探究了各个因素对力学性质的影响。
以上类岩石材料在力学性质方面的研究一定程度上为岩石力学工程中提供了借鉴依据。但是对类岩石材料的强度、脆性特征是否与天然岩石存在相似之处却少有研究。这也导致了部分类岩石材料在荷载过程中出现塑性破坏,且在抗压强度、抗拉强度等力学性质上与天然岩石存在较大差距。为了保证类岩石材料在脆塑性和力学性质与所选砂岩相近,本研究采用正交方法设计类岩石材料的不同配比,并根据Tatone[8]统计的不同产地砂岩50%峰值应力处弹性模量E、单轴抗压强度σc与单轴抗拉强度σt,以及划定的E/σc和σc/σt值的指标为统计范围,确保类岩石材料的基本变形特征、力学特征与选定砂岩一致;同时,通过分析类岩石材料不同因素对其基本力学性质的影响程度并采用多元线性回归分析确认类岩石材料的最优配合比。
1 试样制备与试验方案
1.1 原材料选择
根据分析国内类岩石配比方案[9-11],类岩石材料骨料选取200目石英砂与325目重晶石粉,胶结材料选用425早强型水泥和3.0高强石膏粉。原岩选中粒砂岩,具体物理力学参数见表1。

表1 砂岩基本物理力学参数Table 1 The range of basic physical and mechanical parameters of sandstone
1.2 正交试验设计
正交试验设计采用骨料占总材料质量比(骨料占比)、胶结材料水泥与石膏质量比(水泥∶石膏)、重晶石粉占骨料质量比(重晶石粉占比)作为类岩石材料正交试验的3个因素,每个因素设置5个水平,具体设置见表2。
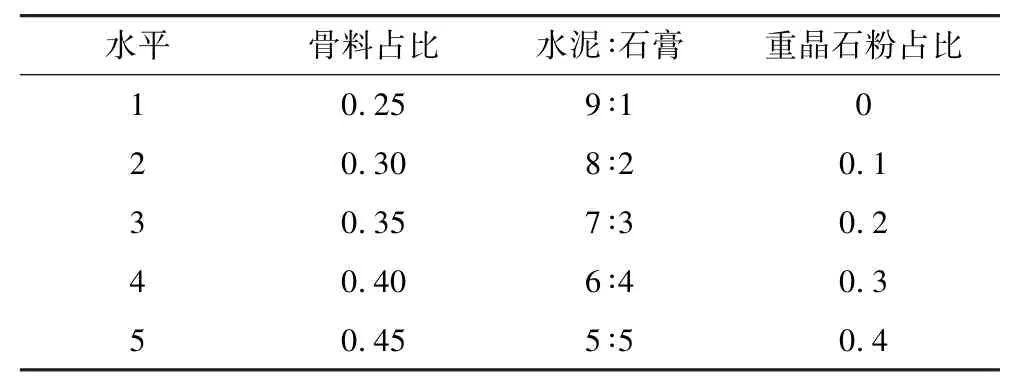
表2 类岩石材料正交试验因素水平设置Table 2 Horizontal setting of orthogonal test factors for rock-like materials
用正交方法设计试验需考虑每一个影响因素的不同水平在设计方案中应出现相同次数,且任意两个影响因素中的不同水平组合在方案中也应出现相同次数,故本试验具体选用6因素5水平的正交试验设计方案L25(56),选取设计方案前3因素水平进行正交试验。其按照正交设计的具体方案如表3。
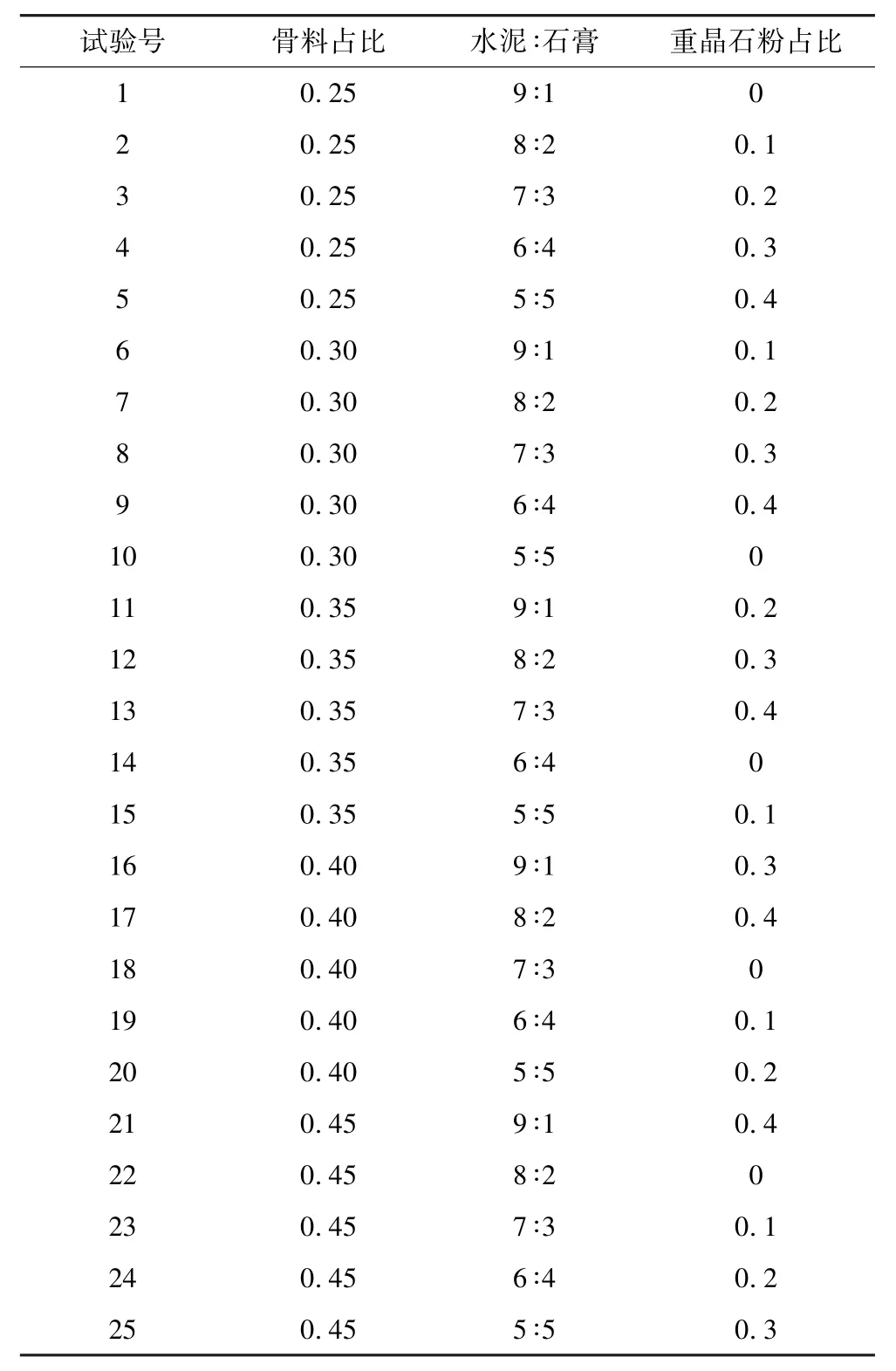
表3 类岩石材料正交设计配比方案Table 3 Proportion scheme of orthogonal design for rock-like materials
1.3 试样制备及力学性质试验
试样制备时,将石英砂、重晶石粉、水泥、石膏放置称重台进行称重(误差≤1%),将称量好的原料进行充分搅拌后添加水。拌合后将物料浇筑进φ50 mm×25 mm和φ50 mm×100 mm模具(图1(a))当中并进行振动和压实。振动和压实可以使试样内部气泡减少,使其内部分布均匀。试样制作完成后静置1 d后进行脱模养护,选取标准28 d养护方式进行养护,养护温度20±1°,养护湿度大于99%。养护完成的试样见图1(b)。

图1 制作模具及试样Fig.1 Molds and test pieces
对养护完成的试样测量基本物理性质和进行单轴压缩试验、巴西劈裂试验,分别测得类岩石材料的密度 ρ0、单轴抗压强度 σc、抗拉强度 σt、50%抗压峰值应力处弹性模量E,具体参数如表4所示。其中,岩石加载系统采用长春科新试验有限公司生产的SAW-2000微机控制电液伺服岩石压力试验机,加载速率为0.1 mm/min。
根据表4可以得出类岩石材料的密度范围为1.80~1.99 g/cm3,单轴抗压强度为 23.22~50.68 MPa,抗拉强度为1.71~4.93 MPa,弹性模量为6.19~14.67 GPa。通过对比表1与表4可以发现类岩石材料的物理力学性质与原岩较为接近,且根据图2比较类岩石与砂岩在单轴压缩试验和巴西劈裂试验的破坏形式,可以发现2类试样在破坏形式上存在相近之处。因此可以依据正交试验方案做进一步分析。

图2 类岩石材料与砂岩破坏形式对比Fig.2 Comparison of failure modes between rock-like materials and sandstone
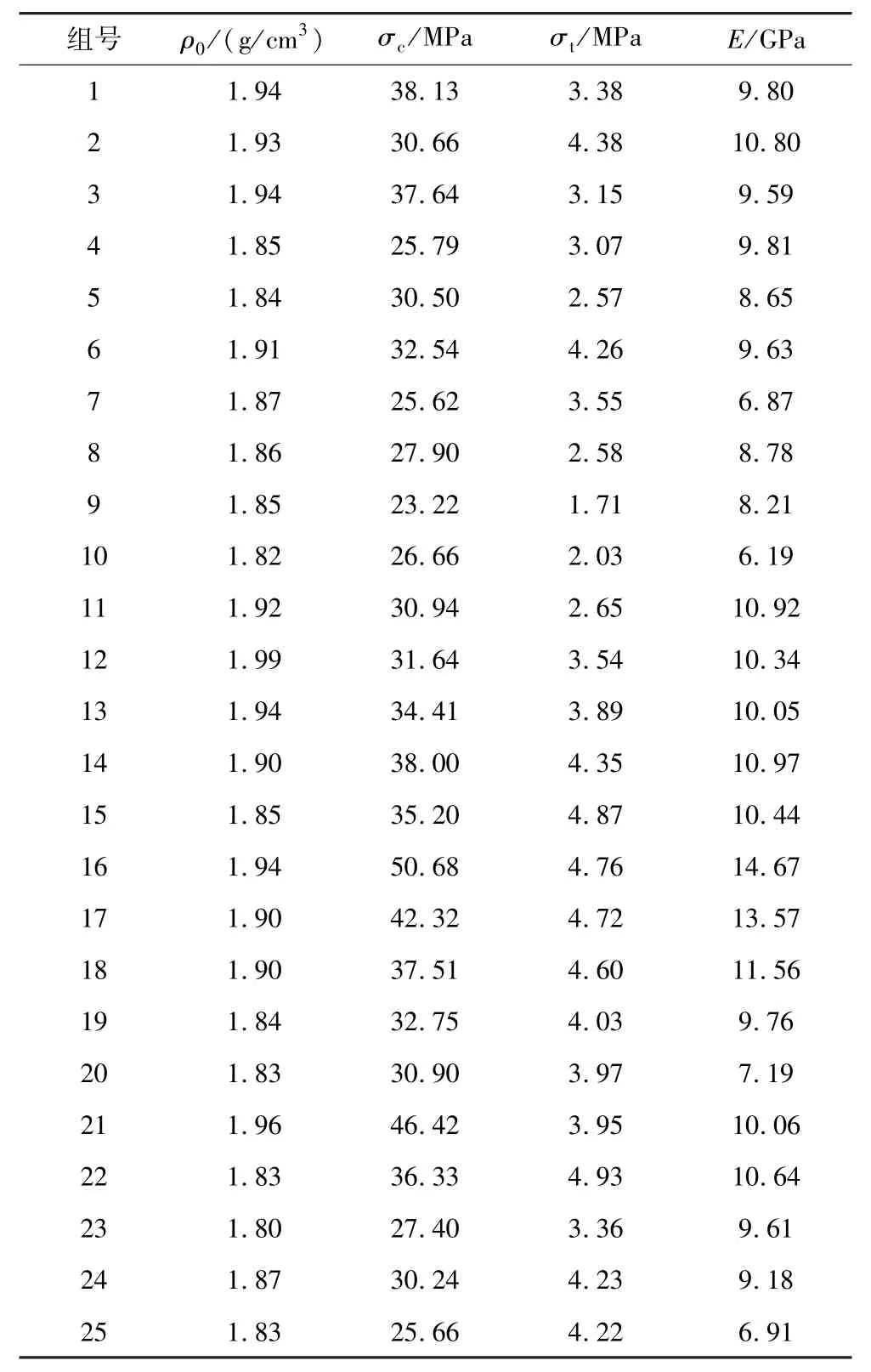
表4 类岩石材料基本物理力学性质Table 4 Basic physical and mechanical properties of rock-like materials
2 试验结果脆性指标分析
为了保证通过正交设计制作的类岩石材料在强度参数及脆性指标上符合原岩的要求,根据Deere等[12]研究的著名分类图表,将50%峰值应力处所对应的弹性模量E与单轴抗压强度σc进行相比,划定高模量—强度比、中模量—强度比、低模量—强度比作为强度参数判别依据,并且依据Tatone[8]在Deere的基础上引入的拉压比σc/σt作为类岩石材料脆性指标的判别依据。
图3、图4分别为25组类岩石材料与天然砂岩E/σc、σc/σt指标比较。
由图3、图4可知,通过将正交设计试验的类岩石材料与所统计的天然砂岩数据进行对比,得到在E/σc方面,25组类岩石材料集中于中模量—强度比区域内,除4、9、21组外,其余全部符合原岩基本变形指标范围;而在σc/σt方面,25组类岩石材料中,符合原岩脆性指标范围的组分别为 1、3、5、8、9、10、11、16、21组。综上分析,同时满足原岩变形指标与脆性指标的为 1、3、5、8、10、11、16 组。 据此判别依据对正交设计试验的类岩石材料进行筛选,从根本上解决了类岩石材料在试验过程中出现强度、弹性模量与天然岩石存在较大差距,在荷载过程中出现塑性破坏等问题,确保了类岩石材料与原岩材料的相似性,为后续敏感性分析奠定了基础。
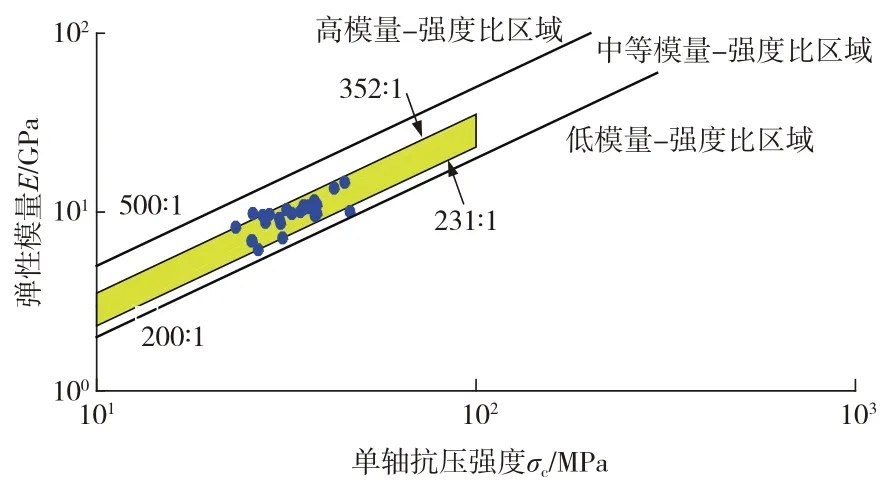

图3 类岩石材料与天然砂岩E/σc指标比较Fig.3 Comparison of E/σc index between rock like material and natural sandstone
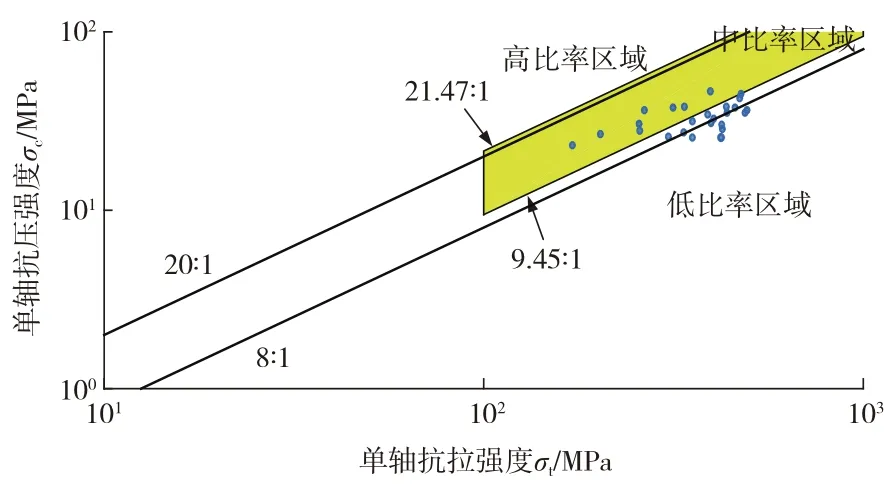

图4 类岩石材料与天然砂岩σc/σt指标比较Fig.4 Comparison of σc/σt index between rock like material and natural sandstone
3 类岩石各影响因素敏感性分析
极差敏感性分析法[10]是针对每一个因素对力学性质参数的极差来分析问题的方法。极差的大小反映了不同因素对参数指标的影响程度。极差大则说明了该因素的不同水平对性质参数影响较大,为重要因素。极差小则相反。利用极差敏感性分析法可以有效地分析各因素对类岩石材料物理力学性质的影响程度。
3.1 密度敏感性分析
计算不同因素各个水平下影响类岩石材料密度的均值与极差,并绘制其直观分析图,如图5所示。图5表明,水泥∶石膏极差最大,重晶石占比极差最小。说明水泥∶石膏对类岩石材料密度的影响最大。值得注意的是,在重晶石占比水平3、4中,两者极差相同,由此说明,重晶石占比在0.2和0.3对类岩石材料密度影响程度一致。
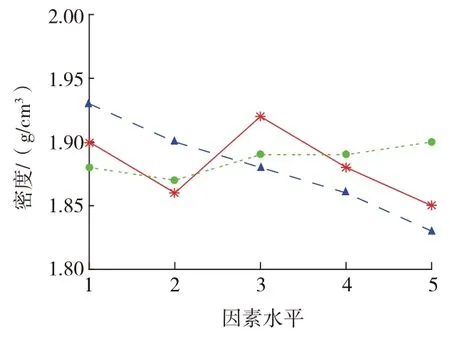
图5 密度敏感性分析Fig.5 Density sensitivity analysis
从变化趋势可以发现,试样密度随骨料占比的增加而呈现先下降后上升再下降趋势,随水泥∶石膏的下降而下降,而随重晶石占比的上升为先下降后上升。
3.2 单轴抗压强度敏感性分析
图6为3因素对试样单轴抗压强度影响的直观分析图。由图6可知试件单轴抗压强度受骨料占比影响最大,水泥∶石膏也有一定影响,而受重晶石占比的影响最小;且试样单轴抗压强度随骨料占比的增加而呈现显著先下降后上升再下降趋势,随水泥∶石膏的下降而下降,而随重晶石占比的上升,试样抗压强度出现较为复杂变化,为显著上升—缓慢上升—缓慢下降—显著上升趋势。
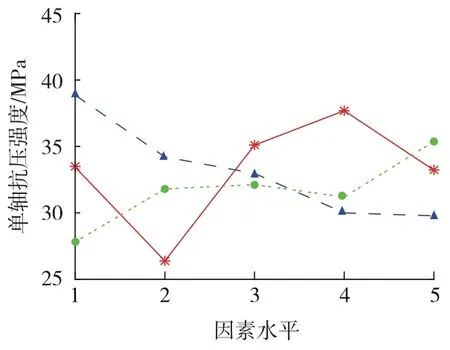

图6 单轴抗压强度敏感性分析Fig.6 Sensitivity analysis of uniaxial compressive strength
3.3 抗拉强度敏感性分析
图7为各因素对抗拉强度影响趋势图。由图7可知,骨料占比对试样抗拉强度起主要控制作用。且抗拉强度随骨料占比的增加而呈现显著下降—上升—下降趋势;随水泥∶石膏的降低、重晶石占比的增加而呈现先增后减趋势。
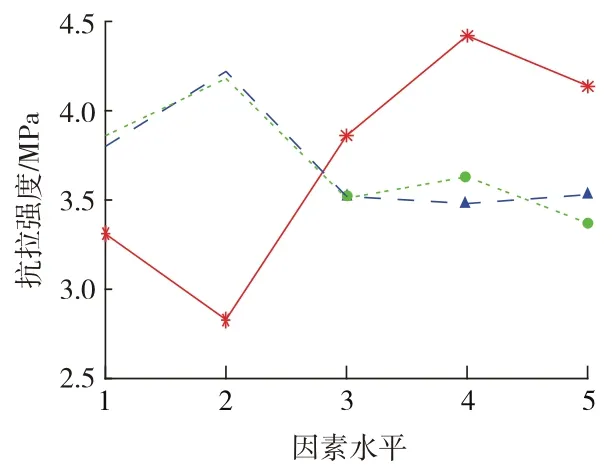
图7 抗拉强度敏感性分析Fig.7 Sensitivity analysis of tensile strength
3.4 弹性模量敏感性分析
图8为各因素对试样单轴抗压强度影响的直观分析图。由图8可知,影响试样弹性模量的主要因素是骨料占比,次要因素为水泥∶石膏,重晶石占比对其影响最小。
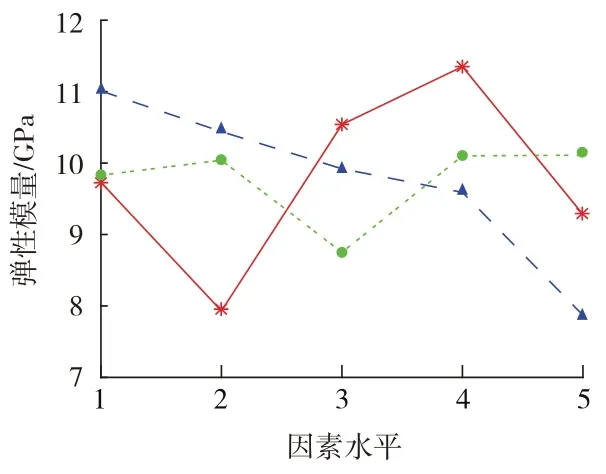
图8 弹性模量敏感度分析Fig.8 Sensitivity analysis of elastic modulus
试件弹性模量随骨料占比的增加呈现显著先减后增再减趋势,而随水泥∶石膏的下降而缓慢减小,反观重晶石占比的改变对试样弹性模量变化趋势影响较小。
4 多元线性回归分析
根据表4统计的类岩石物理力学性质参数,可以清晰地看出,3个因素和类岩石材料性质存在明显的线性关系。故分别将自变量骨料占比、水泥∶石膏、重晶石占比设置为X1、X2、X3选择密度指标为Y1、单轴抗压强度指标为Y2、弹性模量指标为Y3,对其进行多元线性回归分析,可计算出线性回归方程为
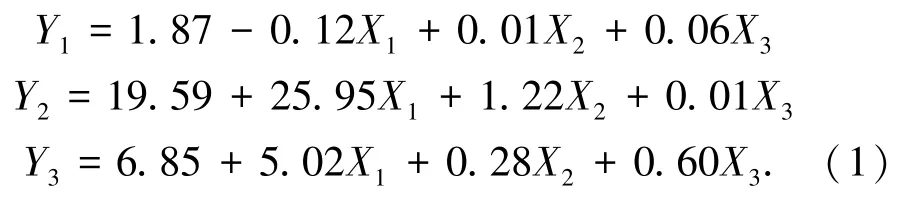
根据式(1)可知,若已知原岩物理力学参数,可以计算出类岩石材料配合比中的骨料占比、水泥∶石膏、重晶石占比。将表1中原岩各参数均值Y1=2.07 g/cm3、Y2=38.70 MPa、Y3=11.75 GPa代入式(1)中,得 X1=0.03、X2=14.93、X3=0.91。 将计算得出的数值代入由表4拟合的抗拉强度回归方程:
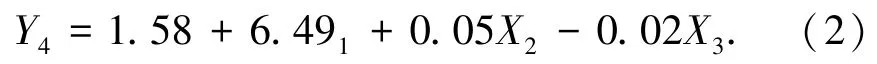
得出Y4=2.51 MPa,与原岩测得的抗拉强度平均值2.72 MPa十分接近,且根据《建筑砂浆基本性能试验方法》[13]中所列出明确规范,回归值与理论平均值差异应在10%以内,通过计算得出抗拉强度回归值与试验值小于10%,说明此经验方程具有一定可信度,可根据此经验方程对相同原材料的类岩石材料进行配比计算。
5 结 论
以石英砂、重晶石粉、水泥、石膏为原材料,通过正交试验设计,以骨料占比、水泥∶石膏、重晶石占比为3个影响因素,每个因素设置5个水平,设计了25组类岩石材料配比方案并测得其物理力学性质指标。
(1)通过比较类岩石材料与原岩E/σc变形指标与σc/σt脆性指标,可以作为判别类岩石材料达到标准的判别依据,且在 25 组配比中,1、3、5、8、10、11、16组同时满足原岩变形指标与脆性指标要求。
(2)依据极差分析法探究了3个因素对类岩石材料物理力学参数的敏感性。研究发现对试样密度起主导作用的为水泥∶石膏,且随水泥∶石膏比例下降,试样密度也持续下降;对试样单轴抗压强度、抗拉强度和弹性模量起主导作用的为骨料占比,且随骨料占比的上升,单轴抗压强度与弹性模量均出现出显著下降—上升—下降趋势。
(3)对25组类岩石材料物理力学参数进行多元线性回归分析,计算得出其线性回归方程并进行演算,结果与原岩数据有较高的一致性,证实了此配比方案的可行性。

