基于有限元的钻进参数相互影响机理研究
毕永升 谭卓英 丁 宇
(1.北京科技大学土木与资源工程学院,北京 100083;2.金属矿山高效开采与安全教育部重点实验室,北京 100083)
在国际岩土工程领域,例如采矿、油气开采、土建、水利水电等工程,为了综合评价地层的岩性情况,经常需要进行钻探勘测工作,而原本钻探勘测工作的费时费力,使得各领域研究人员一直以来都在探索一种简单又有效的方法以获取有关地层地质的工程信息,寻找智能化的钻进技术理论。钻孔过程监测技术(Drilling Process Monitoring,DPM),是一种随钻测量技术,简称DPM系统。在上世纪二三十年代国外石油工业领域开始直到现在众多钻进工程中均有大量的运用,用于测量、监测和记录钻机的钻进参数,现在的钻进参数记录技术就是从其基础上改进而来的[1-4],主要测量和监测钻进参数如推力、转速、扭矩、钻进液压力、振动、冲洗速率及钻进速率等等。从近年来看,Wolcott等人曾建议采用随钻扭矩及轴压来测量原岩强度,Hoberock和Bratcher也曾通过钻速试验来确定原岩抗压强度[5]。Hareland等人运用钻进参数、钻头类型以及地层信息等钻孔数据建立穿孔速率模型,对岩石单轴抗压强度进行计算,建立了基于三锥牙轮钻头的钻速模型,用于岩石单轴抗压强度的估算[6]。在国内方面岳中琦[7-8]详细介绍了原位钻进全过程数字监测技术和处理采集数据的方法,并将原位钻进的全过程数字监测技术应用于香港一实际工程,根据全钻进过程的钻进参数记录数据对地下风化花岗岩地层进行了判层分析。谭卓英等[9]研究了钻进能量、钻进比功用作风化花岗岩地层实时分级的可行性。由此发现钻进过程中改变钻进参数和形式、钻具设备等等都会对作业效率产生影响[10-11],而通过有限元软件进行模拟钻进过程能够更方便有效地对相关猜想进行模拟验证,可以具体到钻头形式、钻进角度、渣土形成及排出等方面的研究[12-14],最大可能地契合实际钻进情况。在此基础上对于钻进参数的利用近几年在神经网络预测方面应用颇多,基于神经网络对钻探数据进行智能分析对自身钻进参数进行智能、快速、准确地调整,以便选择最优钻进方式最大可能缩短钻进工程周期。
以上所述都是对通过钻进参数来确定岩石性质、判断钻进工况以及相关的方法技术的验证和分析,并未对随钻参数与岩体力学参数之间的具体相关性和变化规律进行细致研讨和验证可靠性。基于上述的研究背景,本项目旨在现有的钻探设备基础上,从钻孔常用的三翼PDC钻头入手,对钻头与岩体间的相互作用和钻速、转速、轴压、扭矩等易获取钻进参数的表现与钻头所钻岩体种类之间的关系等进行研究,并结合机器学习的方法对两者间的关系进行分类映射研究验证相关性,以达到利用钻进时所获取的钻进参数来对钻头所钻岩层进行岩性判别的目的。
1 仿真模拟试验分析
1.1 数值模拟的基本假设
钻进过程实际上是一个极其复杂的过程,由于受到具体工程情况中不同的岩石力学参数跟钻进参数影响,以及地理环境因素的影响,会产生各种对应的不同结果。因此为了更加方便准确地从理想状态下对钻进过程进行研究分析,需要做出一些假设:①每层地层都是各向同性的理想弹塑性体,介质均匀,不考虑内部的水跟裂隙;②钻头是刚度跟强度远大于所钻的岩体的刚体,钻进过程不发生变形,且忽略钻头的磨损;③钻进过后的失效土体单元自动消失,以及过程中产生的岩屑不再对后续钻进造成影响;④钻头以垂直于岩石的方向钻进,且钻进轨迹良好,摩擦因数设为定值。
1.2 模型的建立
根据以上假设前提,将岩体定为柔性体,钻头定为刚性体,建立钻进模拟系统。首先在SolidWorks中建立钻头的模型,后导入ABAQUS软件并在Assembly装配模块中与在ABAQUS中已经建好的岩体模型进行装配,钻头和土体的模型如图1所示。此钻进模型模块分为钻头和岩体两部分,钻头模型采用8节点线性六面体(C3D8R)单元,划分网格数为166 496,且被约束为刚体,土体模型采用10节点修正二次四面体(C3D10M)单元进行模拟,划分网格数为22 788,模型总节点数是210 932,单元总数为189 284。需要注意的是在大部分实际钻进情况下,钻头所钻的岩层表面面积是远大于其本身直径截面的,同样只有钻头周边的部分岩体才会受到钻头钻进过程的影响,故基于前人经验本文采用内接圆直径大于钻头外径5倍的长方体岩体模型,并且在装配的过程中要使得钻头的轴线与岩体模型的中轴线重合,钻头在岩体模型的正中心垂直方向钻进。

图1 岩体和钻头模型Fig.1 Model of rock mass and bit
1.3 模拟过程中的问题处理
岩体采用Drucker-Prager模型,以便更加全面地表达出土体非线性、弹塑性、剪胀性等应力应变关系特点,选择线弹性模型作为土体岩性部分的表达,并且在Suboptions下拉菜单Drucker-Prager Creep中定义适当的蠕变模型,与Drucker-Prager模型相耦合可同时计算蠕变和塑性变形。根据已有的实际工程数据和文献资料查询,所采取的钻头的材料性质参数以及各类岩石力学参数如表1、表2所示。

表1 钻头材料参数Table 1 Parameters of bit material

表2 岩体材料参数Table 2 Parameters of rock mass material
在有限元分析中,“接触”是一种典型的非线性接触问题,不仅在于接触面本身的力学模型可能是非线性的,也因为是一种特殊的而不连续约束条件,数值往往不容易收敛。本文针对相关问题做出如下设定:钻头与岩体表面的相互作用类型是表面与表面;分析步过程选择动力、显示,力学约束公式为运动接触法;采用了有限滑移,钻进过程中的接触属性为切向行为,采用摩擦公式“罚”,摩擦系数取0.15。选取钻头顶部中心点为后续模拟主要参考点,对钻头定义一定的转速以及钻速,只保留钻具的轴向移动(y轴方向)和转动自由度,岩石底部设为固定边界条件,底部周边以及底面施加约束进行固定,本文中进行的钻进模拟过程中不会发生任何的位移和转角变化,如图2所示。

图2 岩体底部约束Fig.2 Constraints at the bottom of rock mass
1.4 数值模拟分析
1.4.1 钻头侵入岩体过程分析
观察钻头在开始侵入岩体过程不同时刻的应力云图,如图3所示。钻进过程开始时,破岩侵入过程首先是钻齿在竖向的压力作用下靠近并压入岩体表面。同时在扭矩作用下钻头的转动带动钻齿对土体产生切削,在后面的进程中,在受到上述两种主要作用以及其他的摩擦阻力情况下,钻头整体不断钻入岩体;同时钻土与岩体之间的相互作用面积、作用力以及深度也时刻发生变化。
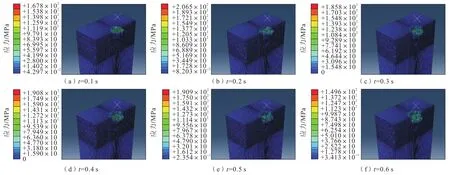
图3 不同时刻的钻进应力云图Fig.3 Drilling stress nephogram at different times
由图3所示的应力云图可以看出从开始到整个钻头完全进入岩体的过程中,岩体表面的应力范围是逐渐变大后趋于稳定,这跟侵入岩体过程中的作用面积和深度有着密切关系。开始接触面积仅仅是钻齿的齿刃,后钻齿切入深度和接触面积变大,钻头也继而进入岩体,作用面积变大。等钻头完全进入岩体后,钻头尺寸固定,作用接触面积几乎不再发生变化,应力云图所示应力也就趋于稳定。通过观察可以发现会出现上下小范围内波动的现象,这是因为前一个土体单元破坏需要一定的时间,彻底破坏后紧接着接触破坏下一个单元体,又是在同种均质岩体单元内进行钻进,故出现相似循环的变化。钻头的轴压力以及扭矩的变化也与之有相近的变化,在钻头刚接触到岩体表面时会突然产生作用力,随着钻齿压入岩体相互作用力逐渐变大,等钻齿完全切入岩体钻头与之接触面积趋于稳定,压力也会趋于稳定,数值大小会在一定范围内波动。
1.4.2 不同岩石在同种钻进条件下的钻进参数分析
将4种岩石均在钻速2mm/s、转速 1 r/s的条件下模拟钻进,以0.2 s的间隔记录各岩石在钻进过程中出现的最大的Mises等效应力如图4所示。从各曲线分布范围可以看出相同的钻进条件下,不同的岩石有着较为明显的应力响应区别,其中煤岩的应力只有13 MPa,而砂岩却能达到100 MPa,性质越好的岩石其最大Mises等效应力也就越高。


图4 不同岩石钻进过程的等效应力Fig.4 Equivalent stress of different rock drilling processes
1.4.3 同种岩石内不同钻进条件下钻进参数分析
设置钻头在钻速2 mm/s、4 mm/s、6 mm/s,转速1 r/s和2 r/s的多种条件下对同种岩石进行的钻进模拟,将钻进过程中参考点的轴压和扭矩记录提出,以分析比较在同种岩石不同钻进条件下钻头的钻进参数表现。以煤岩为例,首先在转速设置为1 r/s情况下进行模拟,逐级提高轴向钻进速度,分析钻头的轴压和扭矩出现的变化及其原因。结果如图5、图6所示。


图5 不同钻速条件下的钻头轴压Fig.5 Bit axial pressure under different drilling speeds
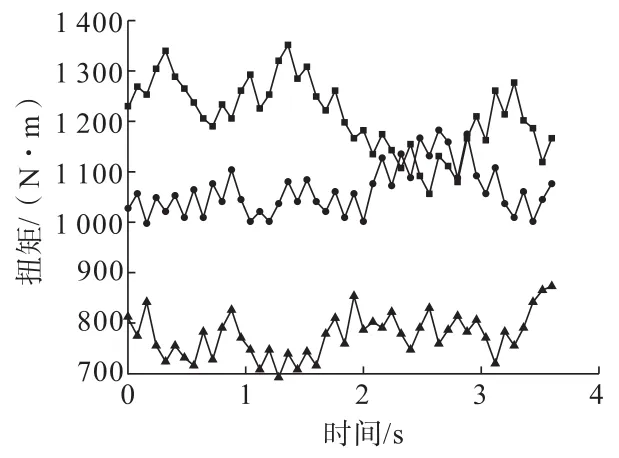

图6 不同钻速条件下的钻头扭矩Fig.6 Bit torque under different drilling speeds
从图5可以看出,随着钻速从2 mm/s增加到4 mm/s与6 mm/s,钻头轴压在12.8 kN为中心的范围波动提升到了以22 kN为中心的范围波动。对于实际钻进过程来说轴压的提升会使钻进速度在一定范围内提高,两者在此期间呈现出了正相关的关系。钻头扭矩的变化与钻头轴压的变化趋势相近,从图6中可以看出随着钻速从2 mm/s到6 mm/s的提升,扭矩也从840 N·m附近提升到了1 200 N·m的程度。原因是钻压的提高能增加钻齿的切入深度,钻齿在旋转能与更多的岩石产生切削作用,从而加快钻进过程继而扭矩自然也随之增加。
再将钻头的转速设置为2 r/s不变,逐级提高轴向钻进速度,模拟得到如图7所示的轴压变化结果。在2 r/s的转速下,轴压随着钻速的提升依旧显示出了逐级提升的现象。但横向比较同钻速下1 r/s的结果,钻头轴压在同级钻速下没有明显的提升现象。如图8~图10所示在相同的钻速条件下转速提高并未引起轴压大的变化,2 mm/s钻速下的轴压仍维持在13 kN附近,4mm/s钻速下的轴压维持在16.5 kN附近,6mm/s钻速下的轴压维持在22 kN。对于钻进模拟来说,轴压的作用即是将钻头压向岩石单元,单纯改变转速更多是对钻头对横向岩石剪切力的改变,所以这部分参数未发生明显变化。


图7 转速2 r/s时钻头的轴压变化
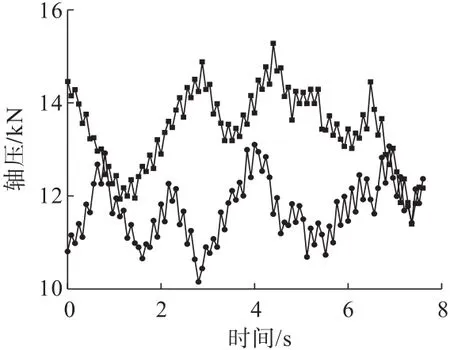

图8 钻速2 mm/s时钻头的轴压变化Fig.8 Axial pressure change of bit at drilling speed of 2 mm/s
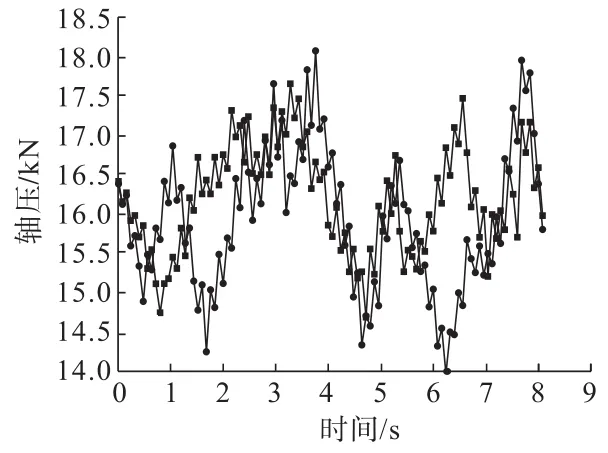
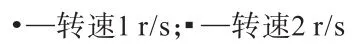
图9 钻速4mm/s时钻头的轴压变化Fig.9 Axial pressure change of bit at drilling speed of 4mm/s
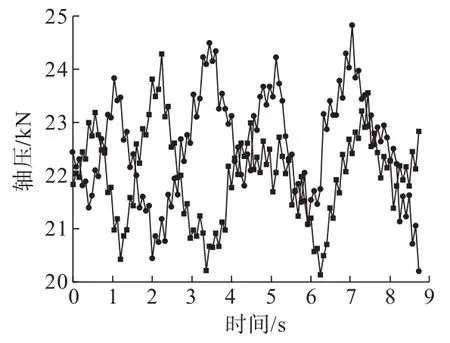
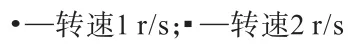
图10 钻速6mm/s时钻头的轴压变化Fig.10 Axial pressure change of bit at drilling speed of 6mm/s
但是在同级钻速下钻头扭矩对于转速的提高呈现出了较明显的反应,如图11所示。对比同级钻速下钻头的扭矩均出现了一定幅度的提高,其中2 mm/s钻速下钻头扭矩从840 N·m的水平提高到了1 030 N·m 左右,4 mm/s钻速下扭矩从1 000 N·m左右提高到了1 275 N·m 左右,6 mm/s钻速下扭矩从1 200 N·m左右提高到了1 630 N·m 的水平,分别如图12~图14所示。扭矩提高的原因是转速提高后,钻头对于岩石的剪切速率增加,使钻头对岩石的剪切力加大,需要更大的扭矩来维持,所以表现出了扭矩的提高。同时从曲线上表现出了转速提高后,扭矩的波动范围也随之提高了一些,钻进的不稳定性相对增加,从模拟结果来看与实际钻进工程中的情况相近。
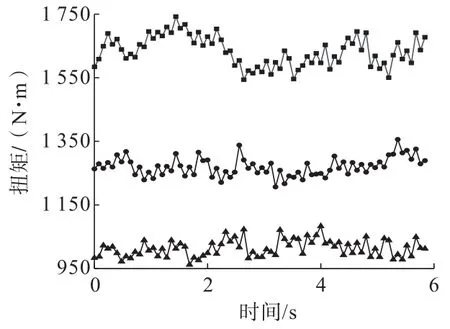

图11 转速2 r/s时钻头的扭矩变化Fig.11 Bit torque change of bit at rotating speed of 2 r/s

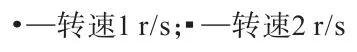
图12 钻速2 mm/s时钻头的扭矩变化Fig.12 Bit torque change of bit at drilling speed of 2mm/s
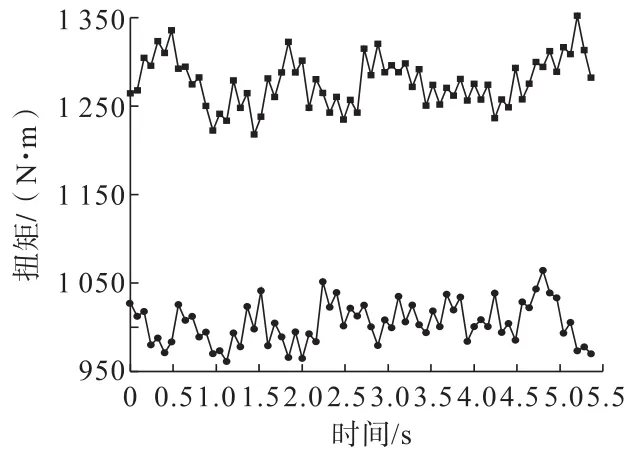
图13 钻速4 mm/s时钻头的扭矩变化Fig.13 Bit torque change of bit at drilling speed of 4mm/s


图14 钻速6 mm/s时钻头的扭矩变化Fig.14 Bit torque change of bit at drilling speed of 6mm/s
由以上分析可以看出,钻头钻进条件的变化会引起钻进参数的变化反应,钻进参数的变化之间是有一定联系的,即使是同种钻头在同种岩石里钻进,一种参数的变化也会引起其他参数的反应,钻进参数之间基于钻头的碎岩机理有着其内在的规律性。
2 Python人工神经网络搭建与训练
2.1 数据的选取整理
2.1.1 数据的选取
数据模拟的结果由岩石类型、钻速、转速、轴压、扭矩5项数据组成,由于模拟时设置了4种岩石在3种钻速和2种转速条件下进行钻进模拟,所以从每种条件下各选取100条数据,一共选取2 400条模拟数据进行人工神经网络的搭建和训练。数值模拟钻进条件数据如表3所示。
实际工程钻孔记录的原始数据为某地应力测量时的钻孔记录数据,数据记录了钻头类型、直径、钻压、转速、钻程进尺、纯钻时间、钻速、岩石类型等数据如表3、表4所示。选取钻头类型、直径、钻压、转速、钻速5种参数为输入数据,4种岩石类型为目标数据共200条数据进行神经网络的搭建和训练。
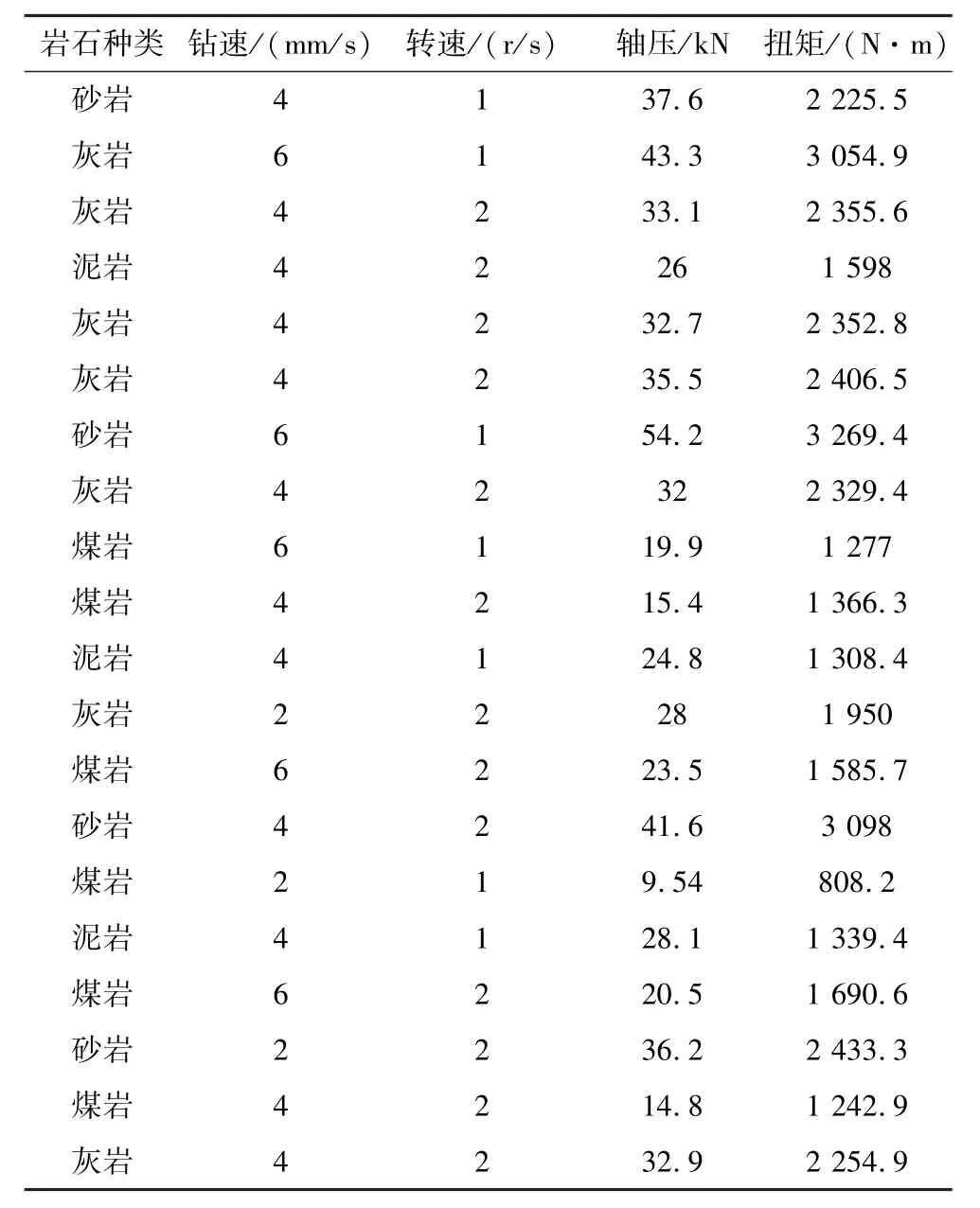
表3 数值模拟原始数据Table 3 Numerical simulation raw data
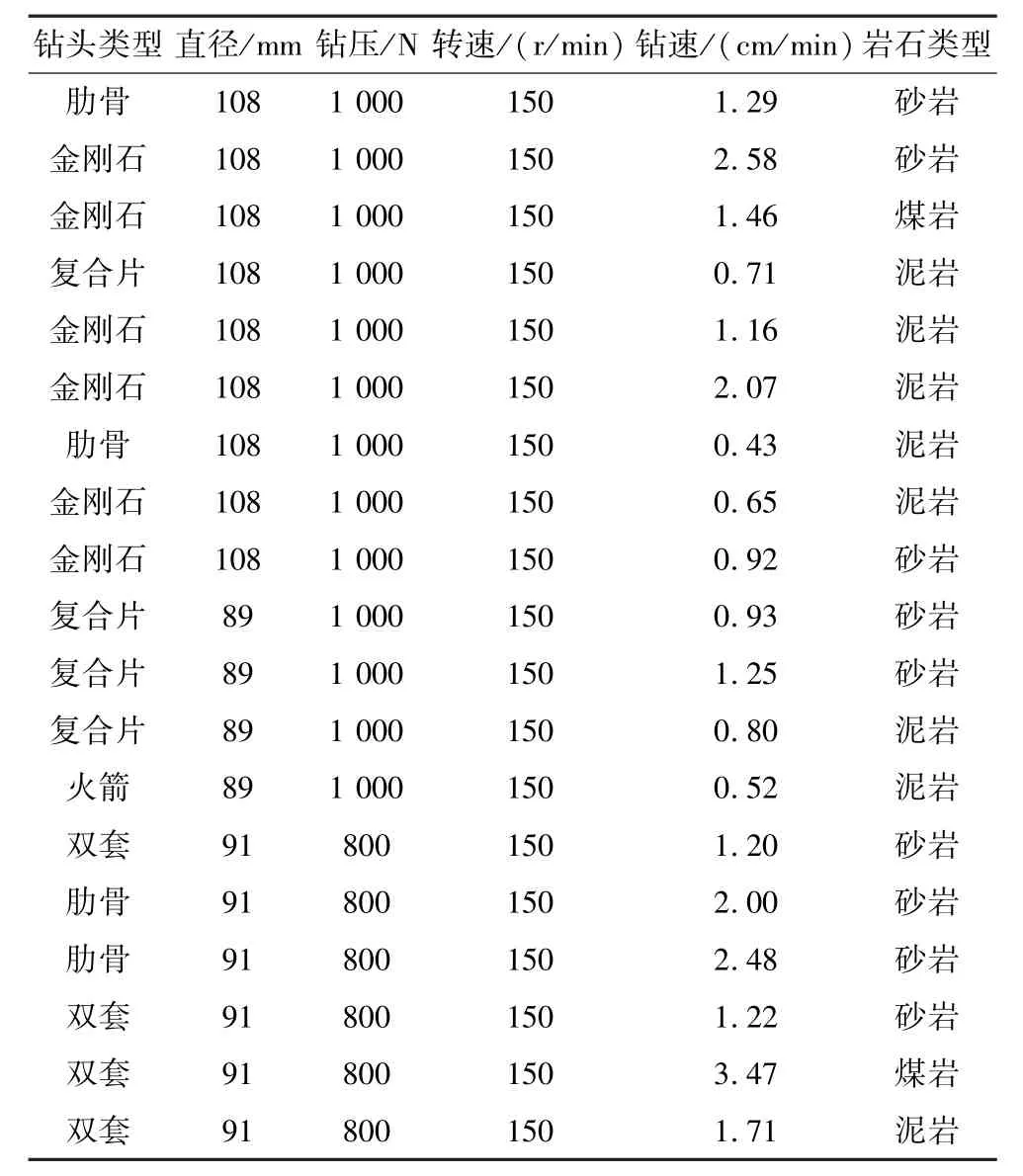
表4 实际钻进原始数据Table 4 Actual drilling raw data
2.1.2 数据的处理
原始数据中的部分指标如钻头种类、岩石种类这种中文属性词,无法直接作为数据被神经网络输入训练,所以需要对其进行转换以符合神经网络的要求。在钻头种类、岩石种类2种指标内,同组的参数之间不具有序列性,也不是进行大小比较的类型,每种指标内的不同参数都是独立又离散的存在,独立编码使用多个状态寄存器来对多个状态进行编码,每个状态都由其单独的寄存器位,一位生效寄存器对应一种状态,具体编码代码图如图15所示。编码后将钻头和岩石种类将被转化为类似数列的形式,如图16所示。可以看到实际钻孔数据已没有中文属性词汇,而且钻头类型也已被转化成了寄存器转态。需要注意的是原始数据在多数情况下不能直接用来分析,需要先将数据标准化进行函数处理,采用数据归一化消除指标数值的范围影响,让不同特征对结果的贡献和作用近似甚至相同,有效地提高模型精度,归一化后输出的数据如图17所示。

图15 编码转换过程Fig.15 Process of code conversion

图16 编码转换后的数据Fig.16 Transcoded data
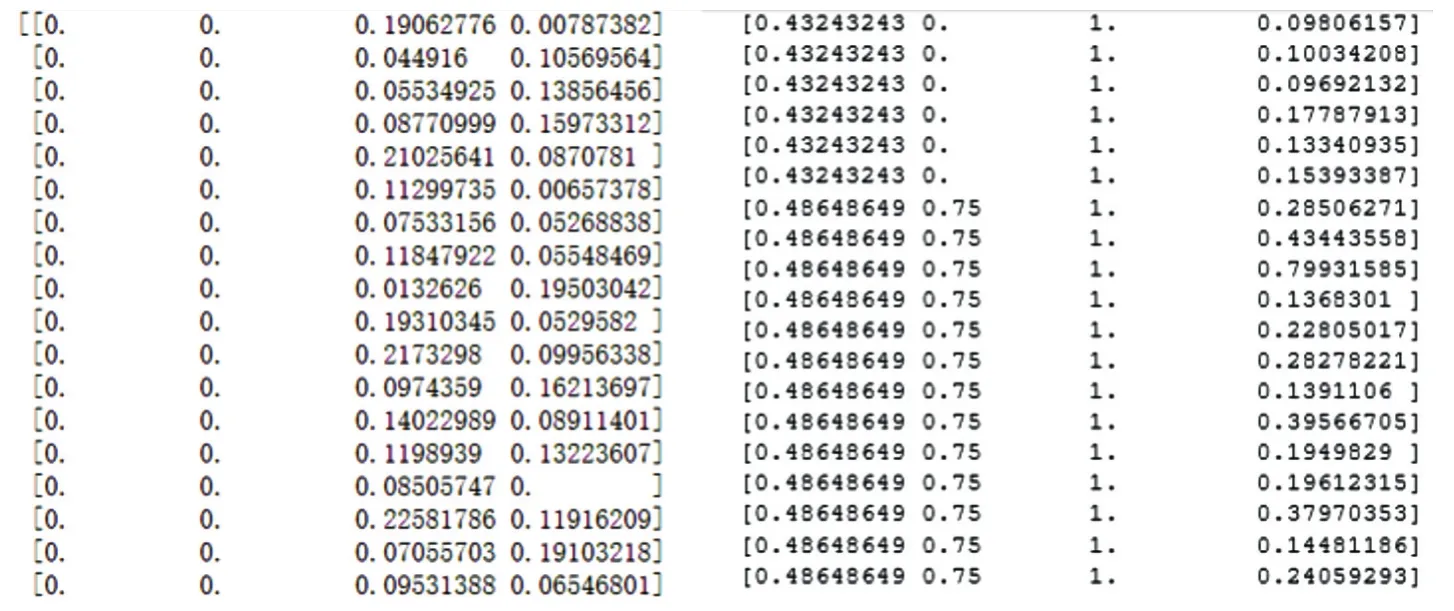
图17 归一化后的数据Fig.17 Normalized data
2.2 关键问题处理设置
为防止神经网络的输入和输出都只在做纯粹的线性交换,本研究采用sigmoid函数作为激活函数,使得神经元的输入、输出转变为具有非线性因素的输入输出。对于模拟钻进数据的模型最后选定3层隐含层,每层12个神经元的结构,对于实际钻进数据的模型选定2层隐含层,每层16个神经元的结构,以使各模型达到较好的训练效果。并且选用交叉熵函数在神经网络模型中前向传播完一次得出一次预测结果后评估预测结果与目标结果之间的相差程度。误差反馈方式则是将损伤函数从网络的最后一层开始,对各节点权重求偏导数,将误差值代入然后对各节点的权重进行调整,即梯度下降法,为了防止梯度一次下降得太快,从而越过了最小值后者说是最优值,所以会设置一个梯度下降的步长系数η来加以限制,同时为防止此反馈方式将所有神经元节点的权值都依次计算梯度下降,造成模型网络计算迭代缓慢,所以选用扩展的梯度下降方法,最终采用混淆矩阵的表示方法对结果进行分析。
2.3 训练结果
2.3.1 实际钻孔数据训练结果
首先对200条实际钻孔数据的神经网络模型设置为只训练的形式进行训练,以分析数据是否具有可训练性,其训练过程如图18所示,可以看到损失函数的值随着训练的进行一直在减小,表示模型建立正确,处于可以正确训练的状态,训练完成后的结果输出如图19所示。
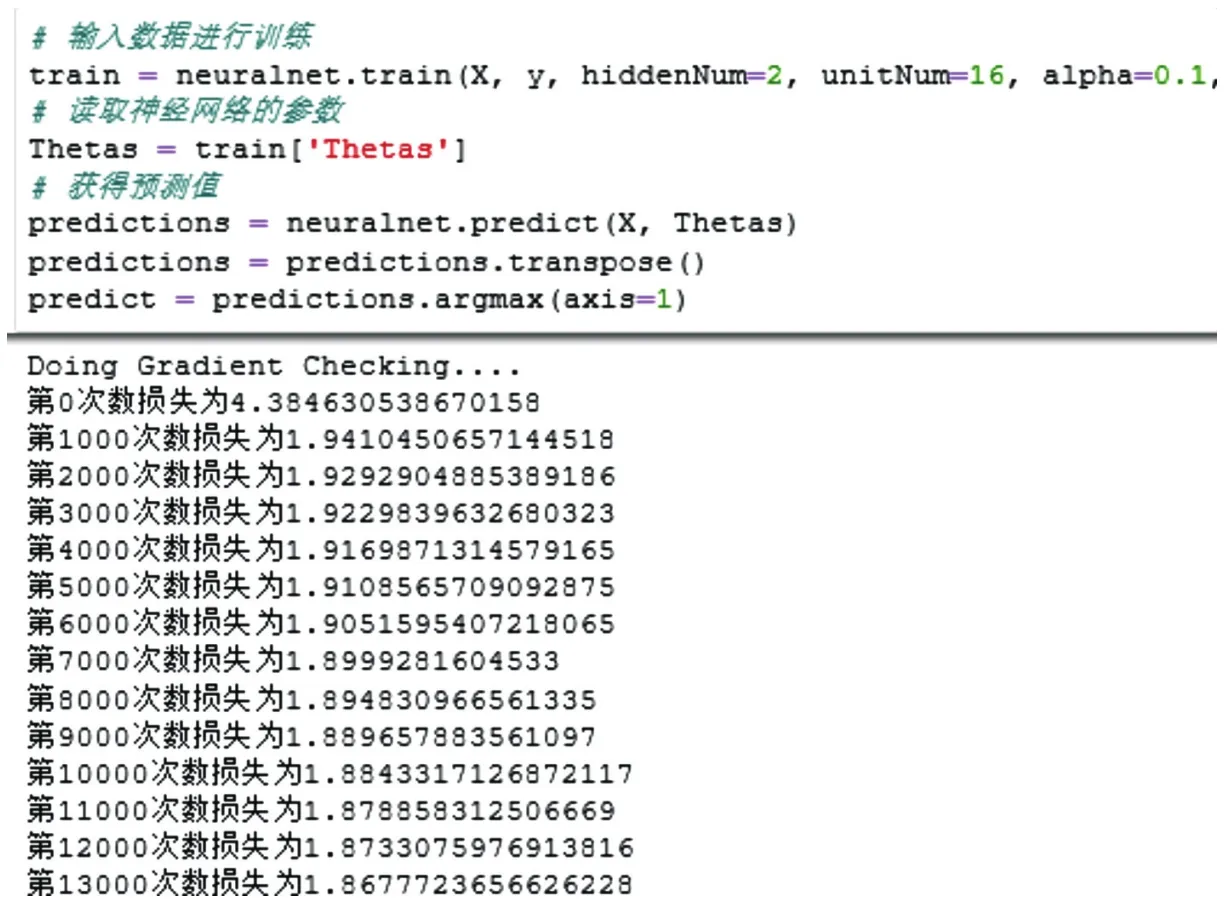
图18 函数下降变化过程Fig.18 Process of function descent change
由图19可以看出,模型整体训练的准确率为89.7%,85个砂岩数据训练正确76个,82个泥岩数据训练正确77个,14个煤岩数据训练正确11个,23个灰岩数据训练正确19个。模型对于各类数据的训练情况较为良好,说明了钻进参数预测岩石类型模型的可训练性,证明钻进参数的数据表现与岩石种类之间是有一定的内在联系的,这点与之前各章节的分析结果相同。然后设置训练集和预测集的训练,将实际钻孔数据设置为随机抽取80%的数据作为训练集数据,20%的数据作为预测集数据,利用训练集数据将模型训练完毕后,代入预测集数据进行预测查看结果,如图20所示。
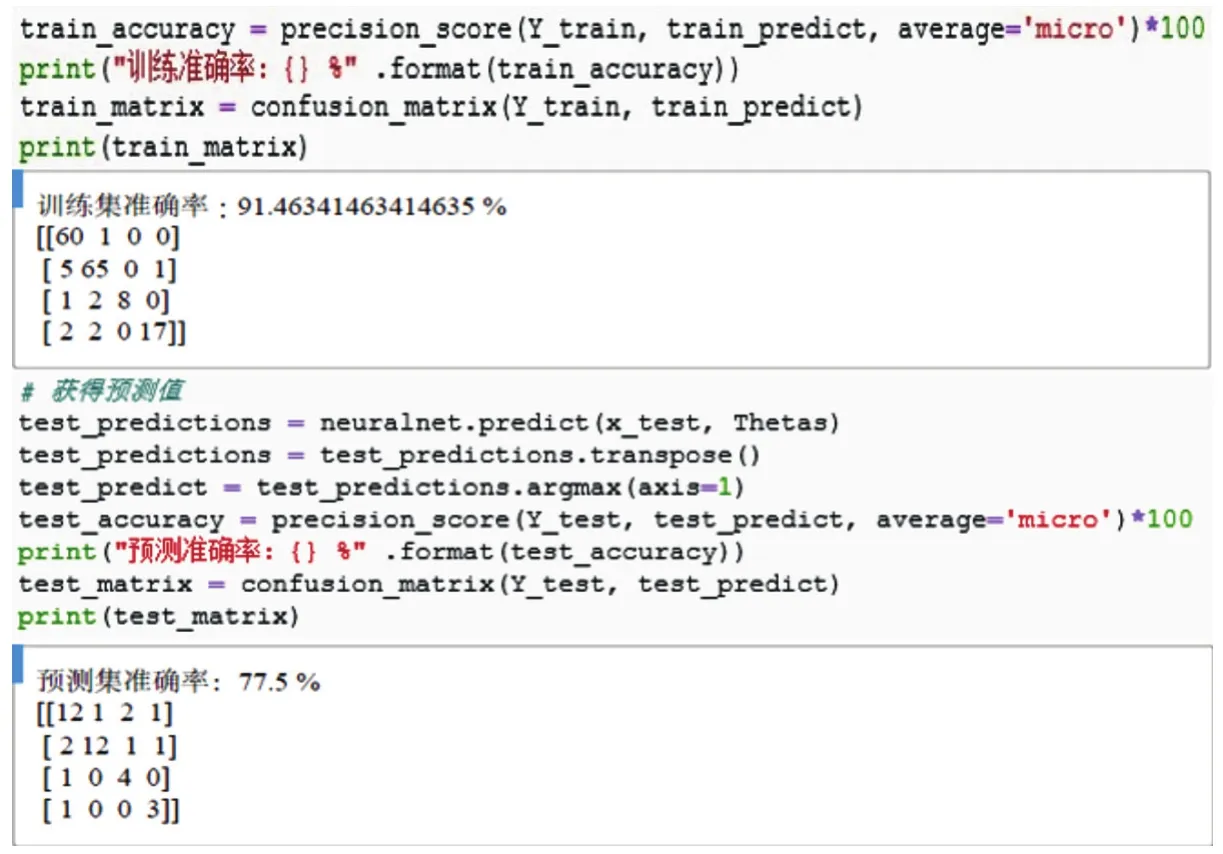
图20 实际钻进数据结果Fig.20 Training results of actual drilling data
对于模型预测集的整体预测准确率为75%左右,抽取的15个砂岩数据预测正确12个,15个泥岩数据预测正确12个,5个煤岩数据预测正确4个,4个灰岩数据预测正确3个。预测准确率没有训练准确率高的原因是由于训练和预测的实际钻孔的数据均较少,即使采取了降低过拟合提高模型泛化的方法,但部分个体的数据仍是无法正确地被模型所拟合预测,这是由于训练样本数据不足所致,但75%的预测准确率表明人工神经网络已能对大部分数据的岩石类型具备可判断性。
2.3.2 数值模拟数据的训练结果
数值模拟数据的训练结果与实际钻孔数据的训练过程相似,将2 400条模拟数据随机抽取200条数据作为预测集,剩余的2 200条数据作为训练集训练。训练集的输出结果如图21所示,整体训练准确率为89.8%,其中551个煤岩数据训练正确523个,543个砂岩数据训练正确468个,536个泥岩数据训练正确503个,537个灰岩数据训练正确452个。

图21 数值模拟数据结果Fig.21 Numerical simulation data results
预测集的结果如图21所示,整体预测准确率为89.1%,与训练集的准确率相近,其中61个煤岩数据预测正确58个,63个砂岩数据预测正确55个,63个泥岩数据预测正确57个,62个灰岩数据预测正确51个。对模拟数据训练预测准确率在90%左右,利用一些模拟时获取的钻进参数能很好地起到对岩石种类预估的效果。
模拟数据预测准确率比实际数据提高很多,一方面是由于模拟训练预测的数据量多于实际数据,数据上的增多使神经网络模型能更好地训练,预测时个体数据的差异影响也会减小,即用更多的数据对神经网络进行训练,神经网络所能识别的数据范围也就更大;另一方面由于实际钻孔工程要比软件模拟时有更多的影响因素和不确定性,获得的钻进参数间的差异可能也就更大,这也影响了神经网络模型对于结果预测的正确性。
3 结 论
(1)利用ABAQUS软件对矿用三翼PDC钻头动态钻进过程做仿真模拟,结果表明:不同的岩石在相同的钻速、转速条件下受到钻头作用力的大小是不同的,砂岩、灰岩、泥岩、煤岩的应力反应依次减小。钻头转速不变时,在不同岩石中提高钻速均会使钻头的轴压和扭矩都增大。钻头的钻速不变时,提高转速均会使钻头扭矩增大,轴压无明显增加。相同的钻速、转速条件下,钻头在不同岩石中钻压与扭矩的输出情况明显不同,钻压与扭矩均是按照煤岩、泥岩、灰岩到砂岩的顺序依次增大。
(2)利用数值模拟数据和实际钻孔数据,使用Python语言进行了人工神经网络的搭建与训练。模拟数据与实际钻孔数据的人工神经网络训练准确率为90%左右,说明了钻进参数预测岩石类型模型的可训练性,证明钻进参数的表现与岩石类型之间是有一定的内在联系的。2个模型预测准确率为90%左右和75%左右,证明利用钻进参数和机器学习的方法来实现对岩石种类的判识具有可实现性。
(3)用软件做钻进过程数值模拟时,所设的一些基本假设例如岩石为各向相同且均质的弹塑性体,还有不考虑钻井液的影响等对模型进行了简化。这些假设使模拟与实际过程有一定的差别,一些实际过程中可能存在的因素被忽略,使模拟结果具有局限性。今后可进一步对模拟模型做出优化修改,使模拟能更加接近实际的钻进情况以能更好研究钻进参数的表现。原始数据量对机器学习的训练和使用效果起着重要的作用,本研究所能利用的实际钻孔数据量有限,利用模拟数据又存在与实际数据有部分差别的可能,所以今后可收集更多的数据以丰富机器学习的数据库,无论对于继续研究还是以后的实际应用都有着重要的作用。

