考虑黏弹性滞后效应的拱坝位移监控组合模型

徐 丛，王少伟,2,3，刘 毅，隋旭鹏

(1.常州大学 环境与安全工程学院，江苏 常州 213164； 2.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038； 3.中国水利水电科学研究院 水利部水工程建设与安全重点实验室，北京 100038)

1 研究背景

位移可直观地反映拱坝的真实工作性态。根据已有监测数据，可建立相应的数学模型，据此对拱坝变形性态进行解释、预测和诊断。目前被广泛应用的数学模型是水压-周期性温度-时效三因果因子的HST(Hydraulic,Seasonal and Time)模型，已经在实际工程应用中取得较好的效果[1-3]。然而在某些特殊环境下，该模型无法解释部分大坝的异常变形性态，需对其进一步优化。针对锦屏一级拱坝历年在1 880 m高水位稳定期监测得到的坝体位移持续增大的异常现象，王少伟等[4-5]通过反演分析发现这种短期趋势性变形是由坝体混凝土的黏弹性滞后变形效应以及气温年周期温降作用共同引起的，并据此建立了考虑滞后变形效应的HHST模型，定量解释了该稳定期径向位移增量中两者所占比例分别为30%和70%。然而，该模型中基于约束最小二乘法建立的滞后水压分量未能充分挖掘影响量和效应量之间的复杂非线性关系，将其融入到HHST模型后，尽管提高了模型对监测变形性态的解释能力，但模型预测能力仍有待进一步提高。

在建立大坝位移监控模型时，单一建模方法难以顾及问题的全面性，而将不同的建模方法进行科学合理的组合，则可以有效发挥每种方法的优点，因而组合建模方法是提高模型解释能力和预测精度的可行方案之一[6-8]。传统的多元线性回归模型(Multiple Linear Regression, MLR)的物理意义清晰，并且可建立具有明确数学表达式的显式型模型，是处理大多数线性问题的首选方法，但其在解决数据量庞大的非线性问题时存在明显的短板，而日益发展的机器学习语言具有十分强大的非线性数据挖掘能力，因此将二者的优点相结合，可以有效地提高模型的性能。此类组合模型主要是以单一模型为基础，然后以组合模型的拟合均方差最小为优化目标，进而确定组合模型中各单一模型的融合权重，王成等[9]和魏博文等[10]结合工程实例，研究结果均表明组合模型具有更好的拟合、预测精度。此外，安全监控模型中输入因子的数量对模型精度也有较大影响，因子数目越多，模型越容易产生病态问题，因而同样采用HST因果因子时，基于有限元模型(Finite Element Model,FEM)水压位移的混合模型的效果通常优于以所有因子作为输入的统计模型[11]。

位移监控模型需要对拱坝变形性态兼具良好的解释能力和预测能力。MLR显式型模型可将监测总位移分解为水压、温度和时效等因果分量，便于变形性态的解释和反演分析；而机器学习模型难以得到因果分量，但其强大的非线性数据挖掘能力有利于提高监控模型的预测精度。对此，本文提出了一种基于HHST因果因子的组合模型建模方法，该模型的本质是混合模型，首先利用FEM计算得到拱坝位移的瞬时弹性水压分量和黏弹性滞后水压分量，并根据建模因子对其分别拟合，其中后者的建模因子多、非线性强，因而采用支持向量机(Support Vector Machine,SVM)对其建立预测模型，再将拟合的瞬时和滞后水压分量融入到HHST模型中，进而基于MLR建立拱坝位移的显式型组合预测模型。

2 拱坝位移HHST模型

监测结果表明锦屏一级拱坝坝体混凝土主要处于黏弹性工作状态，采用图1所示的广义Kelvin模型可较好地表征由坝体混凝土徐变所引起的黏弹性滞后变形性态[5]。

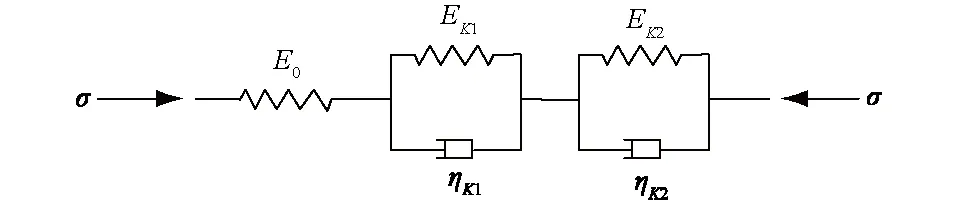
图1 双Kelvin体表征的坝体混凝土黏弹性本构模型Fig.1 Viscoelastic constitutive model of dam concrete represented by double Kelvin bodies

(1)

其中：

(3)

(4)

式中：a0为常数项；X为总水压分量调整系数；t为监测日至始测日的总累计天数；θ=t/100；H为上游库水深；ΔHP1、ΔHP2、ΔHP45、τ为黏性滞后水压分量中建模因子，其具体选取过程和含义参见文献[4]；ai为瞬时弹性水压分量；b1i和b2i为温度分量；ci为时效分量；di为黏性滞后水压分量中的因子系数。

3 支持向量机SVM

f(xi)=ωΦ(xi)+b。

(5)

式中：Φ(xi)为非线性映射函数；ω为法向量，决定超平面的方向；b为位移项，决定超平面与原点之间的距离。

通过引入拉格朗日函数，并求解一定约束条件下的最小化泛函数，上述求极值问题可以转化为一个最优化问题，即

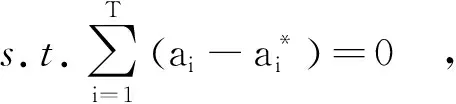
(6)

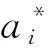
(7)

SVM模型的结构如图2所示，每个节点都代表一个支持向量，将所有节点线性叠加即可得到最终的模型输出值。建立SVM模型过程中最关键的问题是参数优化，本文采用全局搜索能力较强的网格搜索法优化参数C和γ，两者的搜索范围均设置为[2-10,210]。

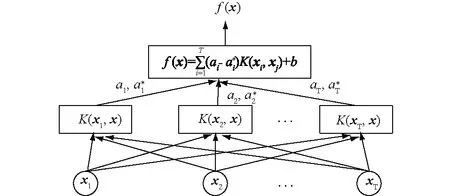
图2 SVM模型结构Fig.2 Structure of SVM model

4 实例分析

锦屏一级拱坝位于四川省凉山州雅砻江干流上，为混凝土双曲拱坝，最大坝高为305 m。坝顶高程1 885 m。2009年10月23日开始浇筑坝体混凝土，并于2013年12月23日全线浇筑至坝顶高程；2014年8月24日，水库首次蓄水至正常蓄水位1 880 m，之后库水位在1 800 m(死水位)至1 880 m之间呈年周期性循环。

4.1 基于FEM的黏性滞后水压位移

锦屏一级拱坝三维FEM如图3所示， 模型计算范围为： 以坝体与坝基交接面最突出处为参考， 向上下游、 左右岸和河床底部各延伸2倍坝高， 坝顶以上延伸1.5倍坝高。 坝体混凝土弹性模量采用前期反演值38.2 GPa[15]， 双Kelvin体中的延迟弹性模量和黏滞系数分别取80、 133 GPa和266、 13 300 GPa/d。模拟过程设置为： 首先分级简化施加坝体自重和1 716 m高程以下库水压力； 2012年11月30日至2018年12月31日， 计算时间间隔设置为1 d，坝体上游水位采用当日实测值，下游水位固定在1 645 m。

图3 有限元模型Fig.3 Finite element model

以PL9-1测点为例，FEM计算得到的黏性滞后位移如图4所示，其中考虑到位移监测数据的连续性，本次建模时段的起始时刻定为2015年6月22日，因此所示位移是以此时刻为基准的相对值。

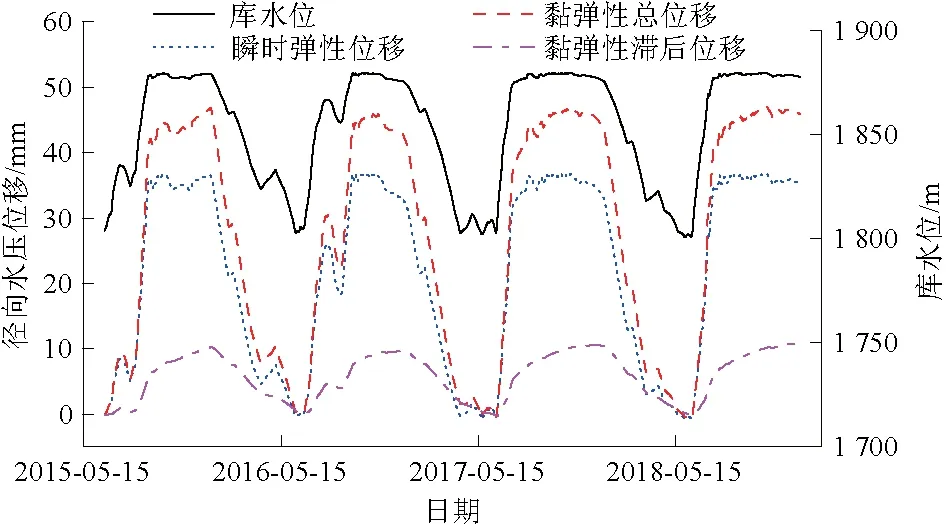
图4 PL9-1径向水压位移FEM计算值Fig.4 FEM-calculated radial hydraulic displacement of monitoring point PL9-1

从图4可以看出：弹性和黏性2种计算模式下，所得径向位移变化规律与库水位的相关性非常强；由于混凝土加载后徐变发展规律是初期变形增长速度非常快，之后则逐渐下降并趋于0，加之蓄水期库水位上升速度非常快，2种因素叠加后使得黏性位移和弹性位移在水位上升期的发展趋势基本一致。尽管有黏性滞后位移产生，但当前时刻的黏性总位移总是完全可以被一个后续时刻高水位时的瞬时弹性位移代替。这也是库水位连续变化下部分混凝土坝不需要单独考虑黏性滞后水压分量的原因，因此以水位快速上升期位移增量反演得到的弹性模量实际应是混凝土瞬时弹性模量和延迟弹性模量的近似等效值。

当水位处于1 880 m稳定阶段时，瞬时弹性位移保持不变(排除库水位波动的影响)，黏性总位移则持续增大;相比于水位上升段，稳定段黏性滞后位移的增长速度已明显降低，此阶段2种计算模式下位移最大差值超过10 mm，约占瞬时弹性位移的30%。库水位下降阶段中，上述位移差逐渐消失，其原因就在于已产生的徐变变形的滞后恢复。此外，黏性计算模式下，相同水位时，库水位年周期下降段的坝体位移值始终大于库水位处于上升段时的位移值，此FEM模拟结果与锦屏、小湾等多个拱坝的位移监测规律相符，由此也表明了黏性滞后水压变形的存在。综上，对于实际运行中的拱坝，同水位时蓄水期和放水期的位移差主要来源于2个方面：库水位下降前累积产生的黏性滞后变形和气温年周期变化中的温降效应。

4.2 基于SVM的黏性滞后水压分量模型

监测总位移中的黏性滞后水压分量是HHST模型的一个重要组成，其预测精度的高低将直接影响整体模型的解释和预测能力，因此需要根据式(4)中该分量的因果因子，首先对其建立高精度的数学模型，此举还可以减少整体模型中的输入因子数，进而避免输入因子过多时的模型病态问题。

根据文献[16]中基于增量距离对锦屏一级拱坝坝体径向位移场的聚类分区结果，本文以第1分区的6个测点为例，将2015年6月22日至2018年6月12日的数据用于模型训练，对2018年6月13日至同年12月31日的黏性滞后水压位移进行预测，其中预测段根据水位变化情况分为2段：6月13日至7月24日为水位上升段，7月25日至12月31日为水位稳定段。PL9-1测点的黏性滞后水压位移预测值如图5所示，其中MLR模型是按照文献[4]中基于约束最小二乘法分段建立的，其他5个测点的整体对比规律与此相似。

图5 PL9-1径向位移黏性滞后水压分量FEM计算值和预测值时间序列Fig.5 Time series of FEM-calculated and predicted values of viscous hysteretic hydraulic radial displacement of point PL9-1

从图5可知： 2种模型的整体拟合结果均与FEM计算值较为接近， 需根据定量评价指标进行进一步量化对比； 上升段中， MLR模型预测结果受库水位波动的影响大于SVM模型； 在稳定段的前期， 由于库水位较为平稳， 两者的预测值都较为接近FEM计算值， 但在2018年11月1日后， 库水位出现了小幅度的下降趋势和波动， 导致MLR模型的预测结果开始出现下降的趋势， 而SVM模型的预测位移曲线则在水位回升后迅速恢复。这说明SVM模型对库水位长周期循环中的短期小幅度波动具有较好的抗干扰能力，预测效果优于MLR模型。

预测阶段2种模型对所研究6个测点的均方误差(MSE)和复相关系数(R2)的统计结果如表1所示。对比发现：所有SVM模型的MSE均小于MLR模型，R2更大。MLR模型6个测点的平均MSE为0.108 7，平均R2为0.987 9；而SVM模型的平均MSE为0.056 0，平均R2达到了0.993 6，即SVM模型的平均MSE比MLR模型降低了48.48%，平均R2提高了0.57%。由此表明，建立该拱坝径向位移黏性滞后水压分量的数学模型时，SVM模型的预测精度明显高于基于约束最小二乘法的分段MLR模型。

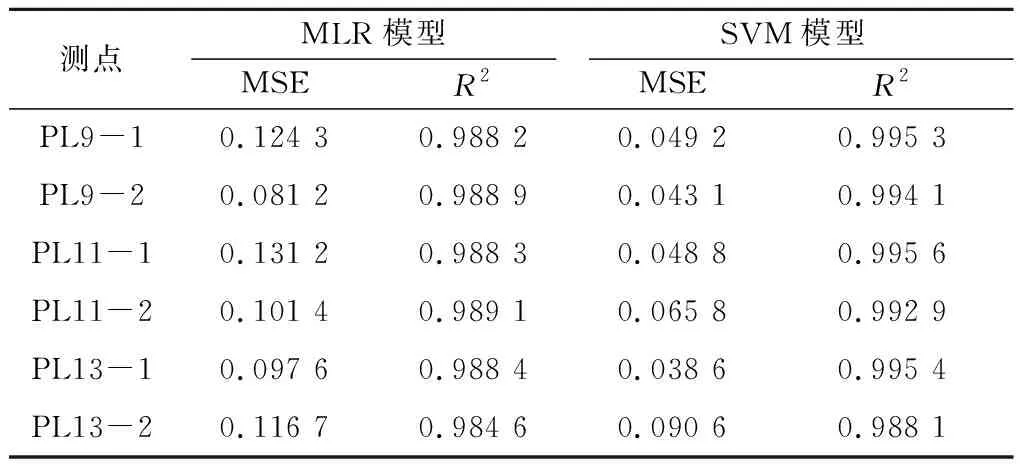
表1 径向位移滞后水压分量预测模型的MSE和R2Table 1 MSE and R2 of the prediction model for the hysteretic hydraulic component of radial displacement

4.3 组合模型的预测结果与分析

组合模型实际上是一个二次建模的过程，首先采用MLR或SVM对FEM计算得到黏性滞后水压位移分量建立因果模型(4.2节)，然后将其与FEM计算并拟合得到的瞬时弹性水压分量相叠加，形成FEM总水压分量；进而按照式(2)所示HHST模型，基于MLR建立显式型的组合模型。为对比分析，本文建立4种模型，分别标记为MLR、SVM、组合模型1和组合模型2，其中前两者直接将HHST模型中的18个因果因子作为MLR或SVM的输入，只包含一次建模过程，且属于统计模型；而后两者则分别采用基于MLR和SVM初次建模的FEM黏性滞后水压分量，通过MLR建立组合模型时的因子数为7个，属于混合模型。PL9-1测点的径向位移实测值和预测值时间序列如图6所示。

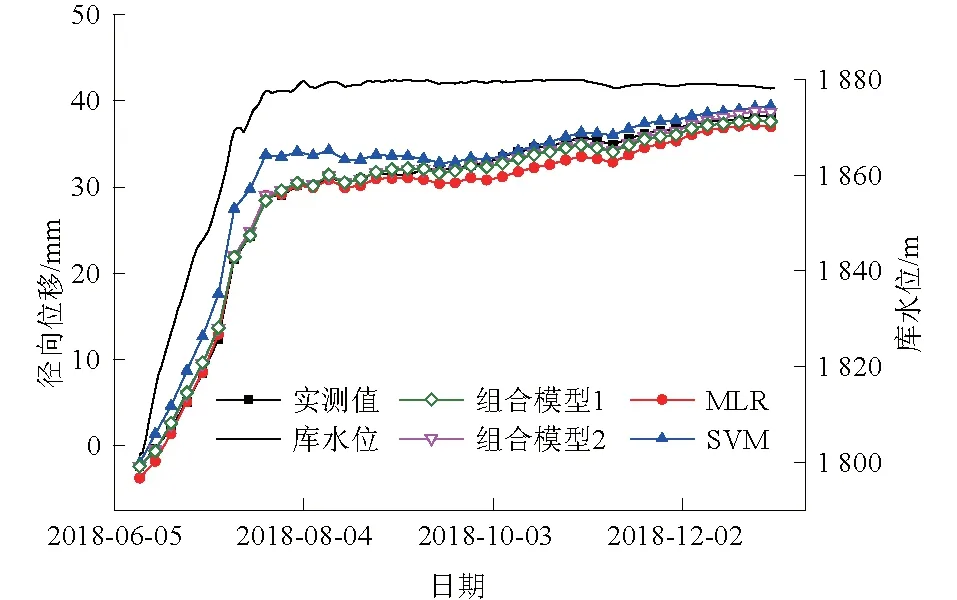
图6 PL9-1径向位移实测和预测时间序列Fig.6 Time series of measured and predicted radial displacement of point PL9-1

从图6可以看出：18因子MLR模型在水位稳定段的预测值明显小于实测值，而18因子SVM模型则是在上升段的预测值明显偏大；2种组合模型的预测序列几乎都和实测值重叠，因此就整体预测效果而言，组合模型显然要优于单一模型。

用4种模型对所研究的6个测点的径向位移进行预测，其MSE和R2的对比结果如图7所示。从图7可以看出：2种组合模型的MSE均明显低于单一模型，R2更高，由此表明组合模型对大坝径向位移的预测效果优于单一模型。进一步对比2种组合模型，除了测点PL11-2外，组合模型2的MSE均低于组合模型1，且R2更高。对于6个测点，组合模型1的平均MSE为0.326 3，平均R2为0.996 8；而组合模型2的平均MSE为0.255 6，平均R2为0.997 5，相比组合模型1分别降低了21.67%和提高了0.07%。由此表明：相比于文献[4]中基于约束最小二乘法建立的分段MLR模型，基于SVM建立的黏性滞后水压位移分量模型有利于提高组合模型的预测精度。

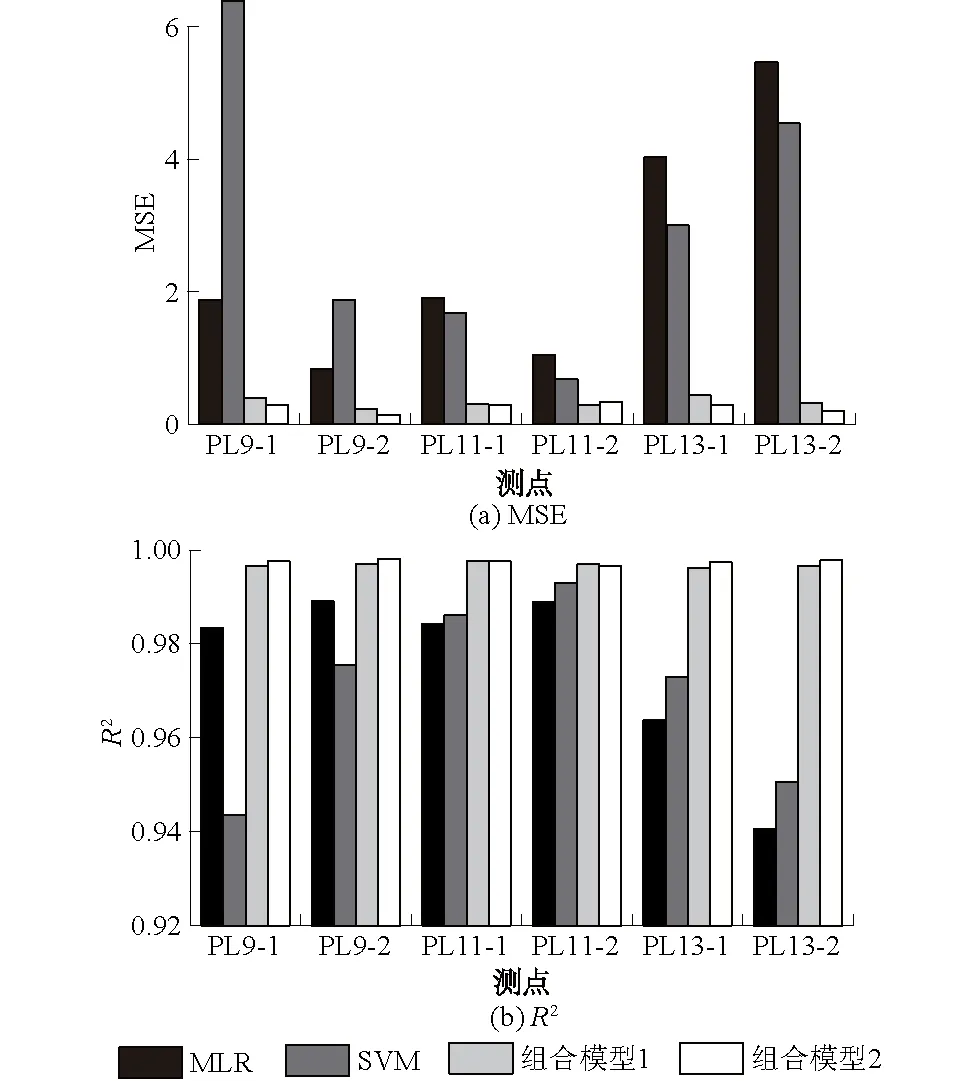
图7 4种模型预测性能的评价指标Fig.7 Evaluation indices of prediction performance of four models

4.4 组合模型的分量分离结果与分析

基于SVM黏性滞后水压分量模型建立的位移组合模型具有最好的预测精度，但该模型对拱坝变形性态的解释能力还需通过其位移分量分离的合理性来作进一步的对比分析。2种组合模型下6个测点的回归系数如表2所示，对PL9-1测点径向位移的分离结果如图8所示，其他5个测点的分量分离结果与此类似。对比表2中的系数和分量分离结果可发现：2种组合模型中，拱坝的径向位移均分解为瞬时弹性水压分量、黏性滞后水压分量、温度分量和时效分量，且模型的回归系数和分量分离结果也十分接近，表明基于SVM和MLR建立的黏性滞后水压分量模型用于组合模型时，所建组合模型具有相近的解释能力，而前者的预测精度更高。

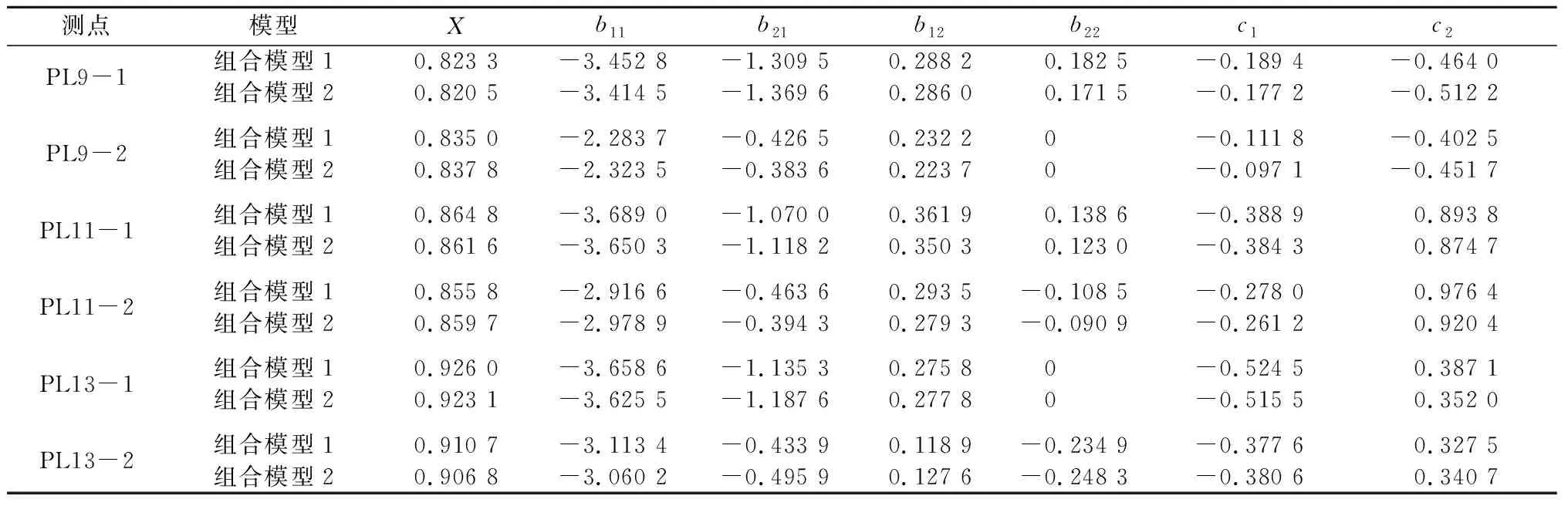
表2 组合模型的回归系数Table 2 Regression coefficients of the combinatorial monitoring models

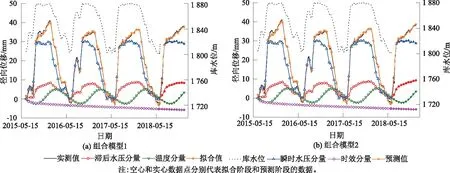
图8 PL9-1测点径向位移实测、预测及模型分量时间序列Fig.8 Radial displacement time series of measured and fitted values, and model components for monitoring point PL9-1

5 结 论

HHST模型可合理地解释锦屏一级拱坝的径向位移在高水位稳定期仍持续增长的异常现象，但其预测能力还有待提升。对此，本文基于SVM对FEM计算得到的黏性滞后水压位移分量建立因果模型，相比于基于约束最小二乘法的分段MLR模型，前者的预测精度显著提升，平均MSE降低了48.48%，平均R2提升0.57%。与多因子单一模型对比，将基于MLR和SVM建立的黏性滞后水压分量用于HHST模型后，所建组合模型的预测效果明显优于单一模型；2种组合模型对拱坝位移变形性态具有相近的解释能力，而采用SVM黏性滞后水压分量的组合模型具有更好的预测能力，多测点径向位移预测评价指标中MSE平均降低了21.67%，R2整体提高了0.07%，表明该组合模型具有较好的位移解释、预测能力，可将其用于拱坝的变形性态诊断。