金刚石衬底上GaN HEMT沟道温度建模：各向异性且非均匀热导率的影响

李 姚,郑子轩，蒲红斌

(1.西安理工大学电子工程系，西安 710048; 2.西安电子科技大学宽带隙半导体材料教育部重点实验室，西安 710071;3.西安市电力电子器件与高效电能变换重点实验室，西安 710048)

0 引 言

随着GaN基高电子迁移率晶体管(high electron mobility transistor, HEMT)技术在商用固态功率开关和RF功率放大器领域的应用，自热效应(高场下，由于声子散射增强导致载流子迁移率退化，从而造成漏电流降低的现象)对器件工作性能和可靠性的影响得到了越来越多的关注。将GaN基HEMT器件与高热导率的衬底材料(如SiC或金刚石)结合可以显著增强器件的热耗散性能。近年来随着人工合成金刚石技术和设备的进一步发展，金刚石衬底上GaN(GaN on diamond, GOD) HEMT器件已被广泛报道，研究表明，相比SiC衬底上的GaN HEMT器件，该结构可以实现RF功率密度的3.6倍增长[1]。

然而，用化学气相淀积(chemical vapor deposition, CVD)技术生长的多晶金刚石(polycrystalline diamond, PCD)薄膜由于在晶粒边界上存在较强的声子散射，会导致其热导率低于体单晶金刚石中的值。此外，PCD复杂的显微结构也会影响金刚石薄膜的热输运特性[2]，成核和合并会在生长界面数十纳米范围内产生高浓度的小晶粒，这些晶粒边界以及可能存在的缺陷和杂质会导致该区域的热导率显著降低；其次，随着晶粒生长，横向晶粒尺寸随距生长界面距离的增加而增大，造成热导率的不均匀性；最后，生长过程中晶粒的竞位生长会导致柱状晶粒结构的形成，最终横向晶粒边界密度远高于垂直方向的晶粒边界密度，导致面内热导率低于截面热导率[3]。因此，为了准确估计GOD HEMT的器件热阻，需要计入PCD衬底不均匀且各向异性的热导率的影响。

Sood等[2]采用时域热反射技术测量了金刚石薄膜的各向异性且不均匀的热导率，并用晶粒边界散射和晶粒尺寸演变有关的模型进行了解释。Anaya等[4]通过改变金刚石生长条件调控金刚石横向晶粒尺寸，增加了金刚石面内热导率，并用晶粒尺寸和晶粒/晶粒界面质量对声子平均自由程的限制进行了解释。Cheng等[5]用时域热反射技术测量了高质量CVD金刚石膜的各向异性热导率，并与理论模型进行了拟合。Song等[6]利用不考虑GaN层中外部缺陷和界面散射的GaN面内热导率，扩散失配模型预测的GaN/金刚石边界热阻和非均匀/各向异性的金刚石热导率，通过有限元计算得到了GOD HEMT器件的最低可能热阻。Zou等[7]用有限元热仿真研究了器件的热耗散过程，考虑了PCD中与深度有关的各向异性热导率，发现金刚石膜生长初期较低的热导率对器件热阻有重要影响。本文中，利用Darwish等[8-10]建立的AlGaN/GaN器件热阻解析模型，研究了PCD衬底各向异性且非均匀的热导率对GOD HEMT器件结温的影响，结合FEM仿真模型提取了衬底的有效热导率，并计算了其与栅长、栅宽、栅指间距、金刚石衬底层厚度以及耗散功率的依赖关系。

1 理论模型

文中采用如图1(a)所示典型的GaN HEMT器件结构。由于AlGaN势垒层通常很薄，仅几十纳米，可忽略其对热阻贡献。同样，GaN和衬底层之间插入的成核层厚度也很小，对热阻的影响也忽略不计。因此，GaN HEMT器件可简化为一个具有两层结构的系统，其顶部具有一个长且薄的热源，底部是一个等温表面。根据文献[8-10]的分析，可将该两层结构分为三个不同的区域，GaN HEMT器件的热阻Rtotal等于这三个区域的热阻之和，即Rtotal=RⅠ+RⅡ+RⅢ。其中RⅠ、RⅡ和RⅢ分别表示区域Ⅰ、Ⅱ和Ⅲ的热阻。

图1 (a)多栅指GaN HEMT器件的截面图，s为栅指间距，Ⅰ～Ⅲ表示不同的热扩散区域；(b)器件1/4结构中区域Ⅰ～Ⅲ的典型等温面图Fig.1 (a) Cross section of multi-fingers GaN HEMT, s denotes the gate spacing, Ⅰ～Ⅲ represent different heat spreading regions; (b) typical isothermal surfaces for regions Ⅰ～Ⅲ in a quarter model of HEMT device

如图1(b) 所示:区域Ⅰ是圆柱形的等温面，圆柱长度沿垂直纸面的方向；区域Ⅱ是长球形的等温面；区域Ⅲ是椭圆柱形的等温面，圆柱长度沿纸面方向。因此，两个共焦等温面AⅠ和BⅠ之间的热阻为区域Ⅰ的热阻，两个半平面共焦等温面AⅡ和BⅡ之间的热阻为区域Ⅱ的热阻，等温面AⅢ和BⅢ之间的热阻为区域Ⅲ的热阻。假设材料具有常数热导率，基于拉普拉斯方程在长球和圆柱坐标系中的解，各区域的热阻具有如下的形式[8]：

(1)

(2)

(3)

然而，材料热导率并不是固定不变的，它通常随温度的增加而减小，满足k(T)=kT0(T/T0)-α，其中α是常数，kT0是温度T0下的热导率，T0是参考温度，T是器件工作温度。在热传导方程中用基尔霍夫变换(Kirchhoff’s transformation)计入热导率与温度的依赖关系后，实际温度可以表示为[9]:

(4)

式中：ΔTlin是线性温度增加量；Tnon-lin表示计入非线性热导率时的温度。

最终，器件的沟道温度可以表示为Tch=TBase+ΔTSub+ΔTGaN，其中ΔTSub和ΔTGaN分别表示衬底和GaN外延层中的温度增量，用耗散功率和各自热阻的乘积(式(1)和(2)(3))计算，TBase表示衬底底部的温度。而为了考虑与温度有关的衬底和GaN层热导率，应用式(4)，对衬底层取T0=TBase，ΔTlin=ΔTSub，得到衬底/GaN层界面真实的工作温度TSub；对GaN层取T0=TSub，ΔTlin=ΔTGaN，得到真实的器件沟道温度TGaN。具体地，TSub和TGaN的计算式分别为[10]：

(5)

(6)

式中：αSub和αGaN是衬底和GaN材料热导率模型中温度的指数项系数。

上述模型考虑了非线性且均匀的材料热导率，较准确地计算了沟道温度。然而，PCD衬底显微结构表征图像中显示[2]，PCD晶粒具有柱状形貌，晶粒边界沿垂直于金刚石生长界面方向。Sood等[2]将PCD晶粒建模为一个从平坦成核层表面生长的梯形区域，平行于界面方向的晶粒尺寸随距成核界面的距离z线性增加，表示为〈dr〉=az+d0，其中d0是成核界面的晶粒尺寸，a是晶粒演变速率，z是距成核界面的距离，该关系可以近似描述为〈dr〉=0.066z+130 nm。垂直方向的晶粒尺寸表示为:

(7)

式中：L表示金刚石膜的厚度；ξ=z/L，β=d0/L；g是生长过程中晶粒存活率的倒数。

考虑到经典的尺寸效应，垂直和水平方向的声子平均自由程λz和λr可以用体金刚石的声子平均自由程λbulk和局部晶粒尺寸〈dr〉和〈dz〉以Matthiessen 定则来计算：

(8)

假设金刚石的平均自由程与频率无关(gray approximation)，取λbulk为1 μm[2]，每个晶粒内的局部热导率可以表示为:

(9)

式中：kbulk为体热导率，根据第一性原理计算取kbulk=3 000 W/(m·K)[11]。考虑到晶粒边界对热流的阻碍，在晶粒中加入了边界热阻RGB，最终净局部热导率可以计算为:

(10)

根据仿真和理论计算[2,5,7,12]，成核界面的晶粒尺寸d0，晶粒演变速率a，生长过程中晶粒存活率的倒数g和边界热阻RGB，分别取值为130 nm、0.066、2和0.1 m2·K·GW-1，由此得到350 μm厚度范围内的PCD热导率如图2所示。

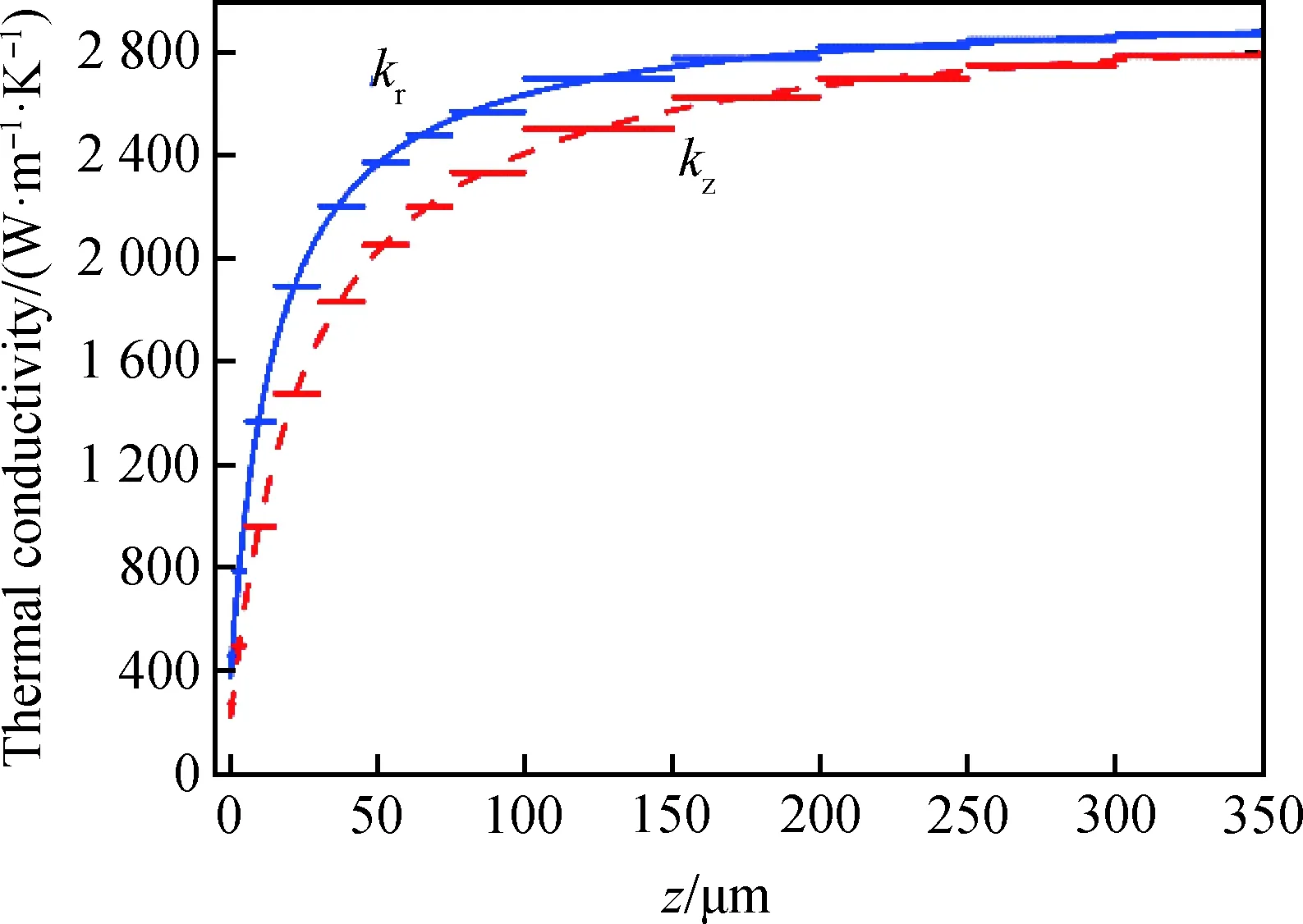
图2 沿面内(kr)和界面(kz)方向的PCD热导率与距成核界面生长深度的依赖关系。图中短划线为各区间热导率沿厚度方向的平均值Fig.2 Relation of PCD thermal conductivity along in-plane (kr) and cross-plane (kz) directions with the growth depth from nucleation interface. Dot dash lines indicate the averaged thermal conductivity over each sublayer

2 结果与讨论

2.1 模型验证与仿真

为了检验计算结果的准确性，用三维FEM热仿真对如图1所示的GaN HEMT结构进行理论建模，提取器件结温最大值。其中，边界条件的设定为[8]：(1)在栅下设置常数热通量作为热源(每根栅指下热源的表面积为Lg×Wg)；(2)衬底底部设置为等温面；(3)除衬底底部外所有表面绝热。计算和仿真中使用的参数列在表1中。此外，为简化计算，对与距成核表面距离z有关的PCD热导率在其厚度方向进行平均。对100 μm厚度范围内的PCD衬底，划分为8个子区域，0～1 μm, 1～5 μm, 5～15 μm, 15～30 μm, 30～45 μm, 45～60 μm, 60～75 μm, 75～100 μm[13]；厚度大于100 μm时，由于PCD热导率变化较小，每隔50 μm进行平均，计算结果如图2中短划线所示。

图3～图7显示了采用面内和截面方向PCD热导率时，计算的结温范围与器件结构参数(栅长Lg、栅宽Wg、栅间距s、衬底厚度t2)和耗散功率Pd的依赖关系，图中点划线表示考虑非均匀且各向异性的PCD热导率时FEM的仿真结果。可以看到，FEM仿真曲线均在考虑面内PCD热导率时的温度范围内，高于考虑截面热导率时的最大温度，沟道温度的变化趋势与解析模型获取的温度上下限基本一致，表明对非均匀且各向异性的PCD热导率，该解析模型也能准确预测Lg、Wg、s、t2和Pd变化时的器件工作温度。图7中还对比了采用均匀的PCD热导率(2 000×(T/300)-0.55W/(m·K))时的沟道温度。可以看到，与非均匀且各向异性的PCD热导率相比，此时的沟道温度有所降低，且该降低量随耗散功率的增加逐渐增大，表明与实际情况更相符的PCD热导率建模对工作在大功率领域的GaN器件的结温和可靠性预测非常重要。

表1 器件沟道温度计算和仿真中默认使用的参数Table 1 Parameters used in channel temperature calculation and simulation

图3 沟道温度与栅长Lg的依赖关系，面内(a)和截面(b)Fig.3 Dependence of channel temperature on gate lengthLg, in-plane (a) and cross-plane (b)

图4 沟道温度与栅宽Wg的依赖关系，面内(a)和截面(b)Fig.4 Dependence of channel temperature on gate width Wg, in-plane (a) and cross-plane (b)

图5 沟道温度与栅间距s的依赖关系，面内(a)和截面(b)Fig.5 Dependence of channel temperature on gate-to-gate spacing s, in-plane (a) and cross-plane (b)

图6 沟道温度与金刚石衬底厚度的依赖关系，面内(a)和截面(b)Fig.6 Dependence of channel temperature on thickness of substrate layer, in-plane (a) and cross-plane (b)

2.2 衬底有效热导率

验证了解析模型的有效性后，通过与FEM仿真结果相拟合，提取了PCD衬底Ⅱ和Ⅲ区域的有效热导率，结果列在表2中。可以看到，对栅长Lg、栅宽Wg、栅指间距s、衬底层厚度t2和耗散功率Pd拟合，得到的PCD层Ⅱ和Ⅲ区域的热导率分别在260～310 W/(m·K)和1 250～1 450 W/(m·K)，相应的拟合曲线如图8(a)～(e)所示。采用上述有效热导率得到的解析计算结果,与FEM仿真获取的最大结温基本一致，证明采用分区域的PCD热导率可以有效预测器件结温。

图7 沟道温度与耗散功率Pd的依赖关系，面内(a)和截面(b)Fig.7 Dependence of channel temperature with power dissipation Pd, in-plane (a) and cross-plane (b)

图8 沟道温度与(a)栅长Lg，(b)栅宽Wg，(c)栅指间距s，(d)衬底层厚度t2和(e)耗散功率Pd的变化关系。其中，实线为解析模型计算结果，散点为FEM仿真结果Fig.8 Variation of channel temperature with (a) gate length Lg, (b) gate width Wg, (c) gate spacing s, (d) thickness of substrate layer t2, (e) power dissipation Pd. Here, sold lines are from analytical model and scatters are from FEM simulation

表2 变参数下Ⅱ和Ⅲ区域拟合的金刚石热导率Table 2 Fitted thermal conductivity of diamond for region Ⅱ and Ⅲ

3 结 论

利用解析模型计算了常规GaN HEMT的器件热阻，考虑了各层材料热导率与温度的非线性关系以及各向异性且非均匀的PCD层热导率，由此得到的器件沟道温度范围被FEM仿真数据所验证。通过拟合FEM仿真得到的沟道温度与栅长、栅宽、栅指间距、衬底层厚度和耗散功率的依赖关系，提取了Ⅱ和Ⅲ区域恒定的PCD热导率，分别为260～310 W/(m·K)和1 250～1 450 W/(m·K)。