温室甜椒采摘机器人识别与采摘系统
薛日新
(池州学院,安徽 池州 247000)
当下随着人口出生率下降和农村人口老龄化的问题逐渐凸显,我国农村劳动力短缺矛盾加剧。针对这一问题,研究人员提出了一些自动温室园艺系统。农业技术蓬勃发展,温室园艺采摘在全世界广为传播,温室如图1所示。温室表面覆盖着乙烯基片,防止蔬菜受到大风、恶劣天气、有害昆虫等农业敌人的伤害。温室园艺有助于农产品更有效地生长,并由于温度适宜而保持较高的生产质量。温室园艺具有自动温度控制系统、自动浇水系统、自动采摘系统等[1-2]。对自动温度系统和自动浇水系统进行研究,讨论如何通过采摘机器人完成农作物采摘工作。

图1 温室照片
采摘机器人在水果识别、采摘系统、移动系统等方面存在困难。水果的识别是使用相机通过图像处理进行的[3]。因此,对茄子、番茄等特殊颜色的采摘机器人系统进行研究尤为重要。虽然甜椒是温室园艺中的主要农产品,但其采摘机器人尚未被研究,其原因为甜椒主要有绿色和黄色两种,其中绿色甜椒的颜色几乎与叶子相同,并且难以识别[4]。
研究甜椒采摘机器人的技术可行性,采用图像处理技术,建立甜椒位置定位及识别模型,构建采摘摄像定位系统。首先介绍大棚甜椒的采摘操作,其次对甜椒采摘机器人进行了概述,并详细介绍了机器人的模型。该模型具有欧拉手腕的六轴机械手结构允许位置和方向运动学的解耦,该解耦的几何特征是最后一个树关节轴的交点。因此,它们的逆运动学问题相当简单。另外,由于具有偏置腕关节(其三个轴不相交于一个公共点)的一些6自由度机械手的方向和位置是耦合的,所以这类机械手不能产生适合解析解的方程。在这种情况下,采用数值方法求解运动学逆问题,并解释甜椒控制系统的识别系统,最后介绍了实验结果。采摘系统的性能取决于甜椒果实的识别效果,并验证了采摘机器人的运动控制算法。
1 采摘机器人
1.1 采摘作业
甜椒树及甜椒的生长情况如图2所示。寻找符合其大小/形状标准的甜椒,符合标准的甜椒可被采摘,切下所选甜椒的茎,并放入容器中。

图2 甜椒生长照片
1.2 功能介绍
研究开发的甜椒采摘机器人,能够准确识别甜椒和采摘茎,同时将甜椒放置在容器中。甜椒采摘机器人的功能如图3所示,需要依靠机器人完成产品识别、采摘和移动功能。利用平行立体视觉的图像处理系统,依赖视觉反馈来间接控制机器人运动[5]。
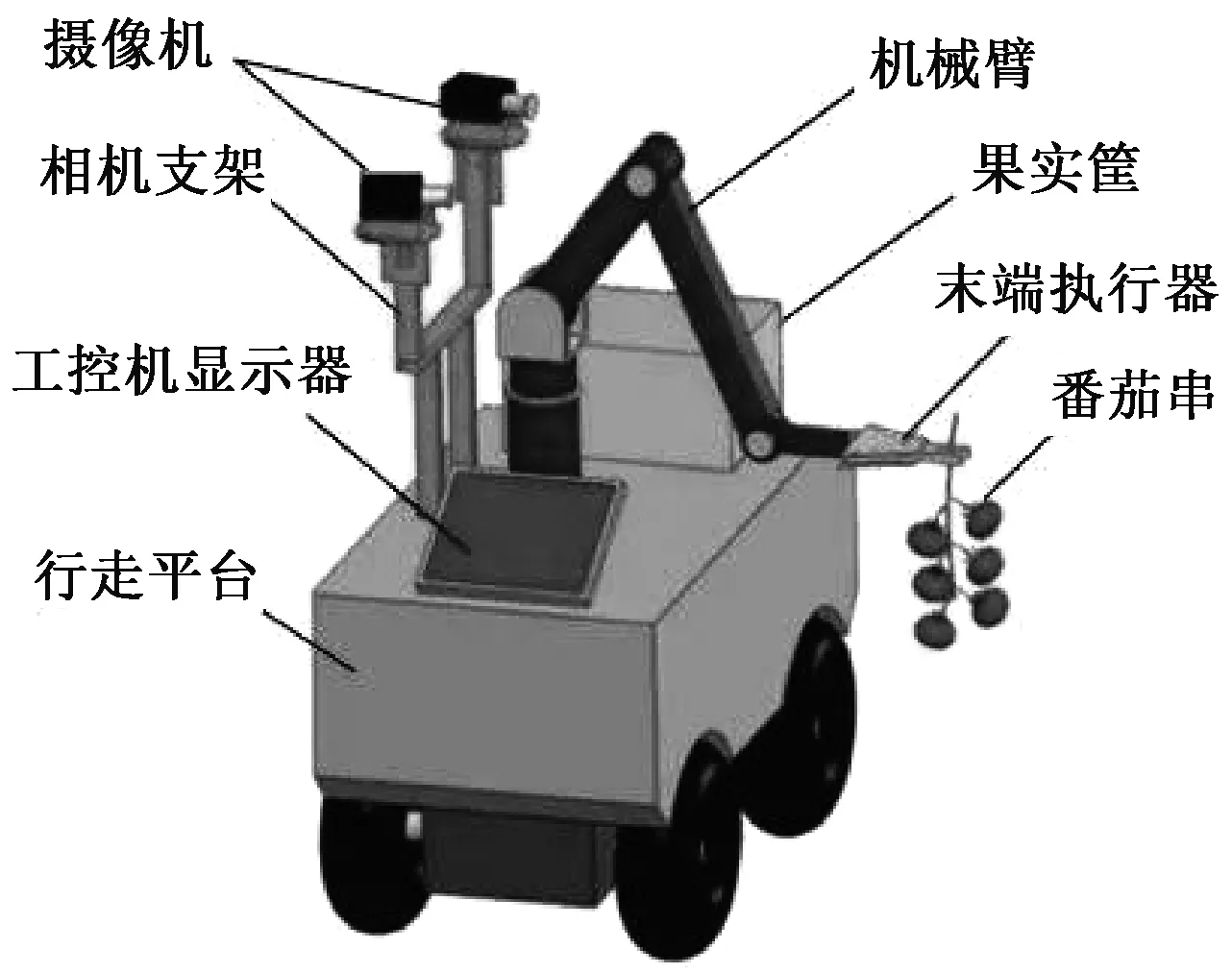
图3 采摘机器人的功能结构
图4显示了采摘机器人的照片。该机器人宽约为1000mm,深为550mm,高为1400mm。当采摘机器人的车轮不转动时,机械操作范围是水平方向的230mm、垂直180mm、深180mm内。采摘装置固定在摄像机框架上,在上述范围内,机器人能够采摘甜椒茎。

图4 采摘机器人工作图
2 机械臂运动学建模
考虑一个6自由度机械手(斯坦福机械手),其刚体和坐标系的分配如图5所示。操纵器有一个Euler腕部,其三个轴在一个公共点相交。第一个(RRP)和最后三个(RRR)接头是球形的。P和R分别表示棱柱形和旋转接头。建立6自由度机械臂模型的坐标系由这些变换矩阵推算出逆运动学反解,从而计算出机器人末端位置处的各关节旋转角度。
2.1 坐标系建立
坐标系建立说明:图5中{1}—{6}代表六个关节处的坐标系,为简化转换矩阵将他们的Z轴方向均定义为竖直向上,Y轴水平向右,X轴垂直于纸面向外。坐标系{i}(i=1,2,3)的原点定义为i轴轴线与i轴和i+1轴轴线公垂线的交点,腕关节坐标系{i}(i=4,5,6)坐标原点定义为4轴轴线与5轴轴线交点处。坐标系{0}是机器人的基坐标系,当坐标系{1}没有相对转动时,坐标系{0}与坐标系{1}处于重合状态;坐标系{E}是机器人6轴末端坐标系,其原点为机器人6轴轴线与末端端面交点;坐标系{S}是力传感器坐标系,其原点为力传感器轴线与其端面的交点;坐标系{T}是工具坐标系,其原点为工具末端端面中心。与前面6个坐标系相同,为了简化转换矩阵,将坐标系{E,S,T}的各轴定义在相同方向,Z轴均水平向右,Y轴竖直向下,X轴垂直于纸面向外。
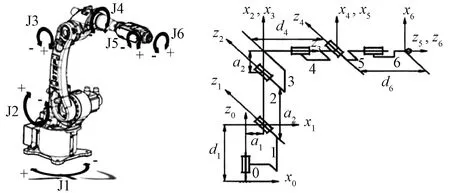
图5 机器人运动学建模
机器人杆件参数说明:
Di:机器人i轴轴线与i+1轴轴线公垂线的距离(i=1,2,3)。
D4:坐标系{3}原点沿Y3方向移动使Z3和Z4共线所移动的距离。
D5:坐标系{6}和坐标系{E}原点之间的距离。
L1、L2、L3:分别为坐标系{S}原点到坐标系{T}原点X、Y、Z三个方向的距离。
L4、L5、L6:分别为坐标系{E}原点到坐标系{T}原点X、Y、Z三个方向的距离。
L7、L8、L9:分别为坐标系{E}原点到坐标系{S}原点X、Y、Z三个方向的距离。
2.2 运动学正解
机械手由一系列连杆末端执行器连接组成,正向运动学即采用关节变量计算末端执行器的位置和方向。Denavit-Hartenberg方法是描述机器人运动学最常用的运动学分析模型方法。
根据机械构型,求得各连杆变换矩阵后,得到总体转换矩阵如下,总体正解为正确的运动学正解。
2.3 运动学逆解
串联机器人逆运动学求解过程需要长时间机械控制完成,逆运动学求解法包括几何法和代数法两种[6]。从几何方法开始,如图6所示,首先定义一个平面,将六轴机器人映射到一个平面内。
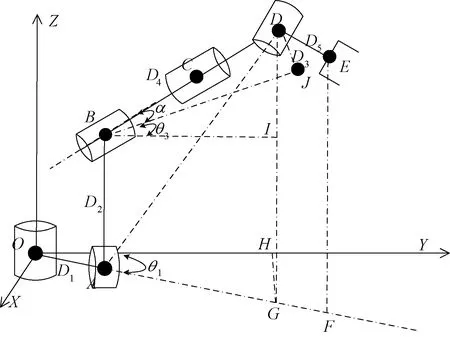
图6 机器人运动反解图
3 机器人系统
3.1 图像处理系统
3.1.1 图像处理系统
图像处理系统包含两个CCD摄像机、图像处理模块和一个捕获板。相机射频采用高质量68万像素的摄像机,捕捉板选择Leutron的PicPort,图像处理系统采用MVTec的HALCON设备。将两个彩色摄像机水平放置,用立体视觉方法检测甜椒的位置。
3.1.2 摄像机定位系统
图7所示为摄像机拍摄甜椒的过程,为了采摘识别的甜椒的茎,定位系统使用带有摄像头的反馈回路来识别甜椒。在这个定位系统中,摄像机可以在三个维度上跟随甜椒进行定位:水平方向,垂直方向和深度方向。图像处理系统识别到甜椒的具体位置之后,向控制器发送相应信息,机器人按照收到的信息控制摄像机位置。

图7 摄像机拍摄甜椒的过程
3.2 图像处理算法
图8为HSV的六棱锥模型。在图像处理算法中,其通过HSI颜色规范的二值化来识别甜椒的果实[7]。HSI颜色规范系统是彩色图像表达的一种,它由色调、饱和度和强度三个图像组成。
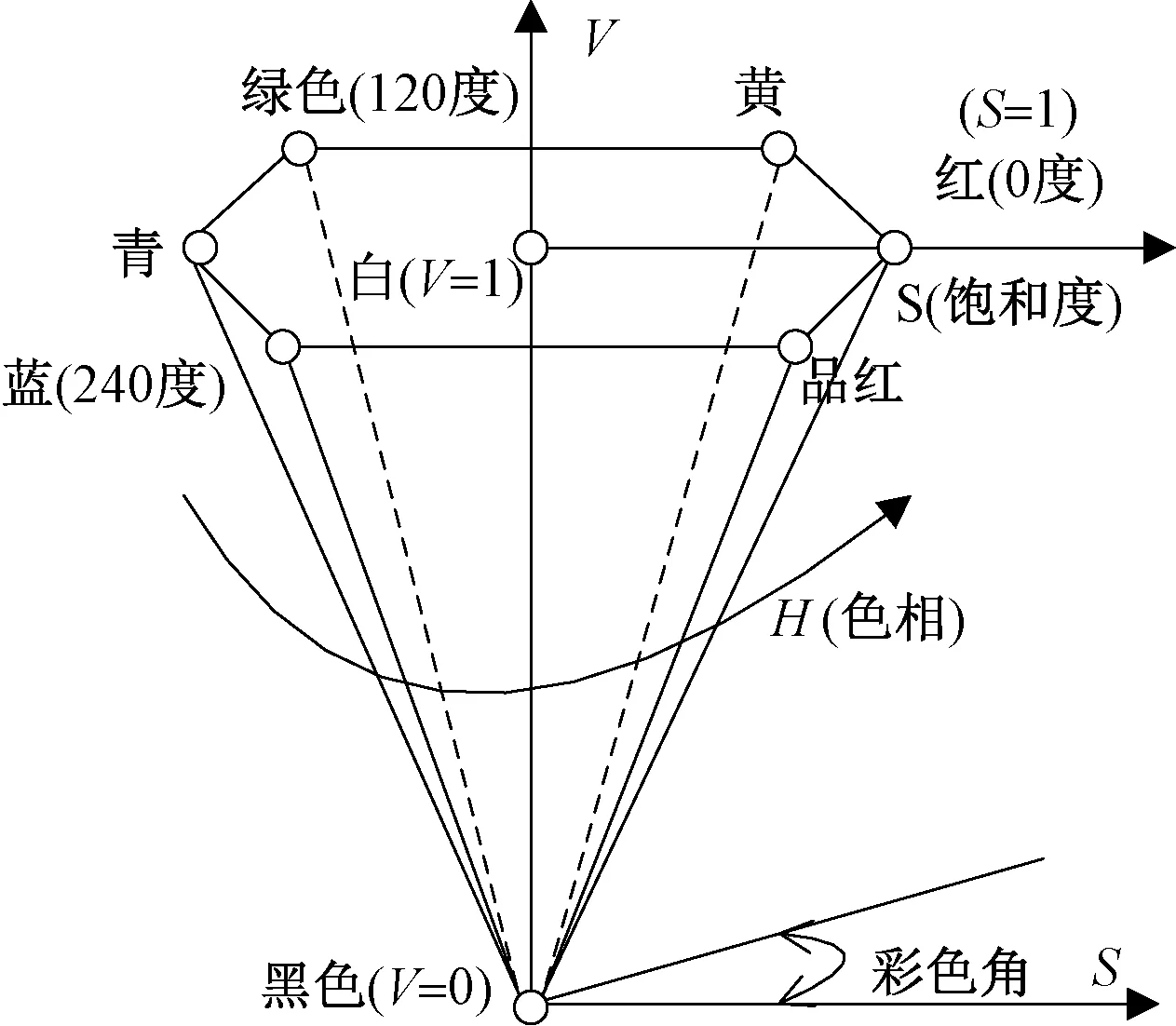
图8 HSV的六棱锥模型
则从RGB到HSV的转换及实现公式如下:
V=MAX(R,G,B)
S=(V-MIN(R,G,B))×255/V
识别算法的流程图如图9所示。首先机器人按照既定的路径运行到拍照位置,发射拍照命令并完成产品拍摄,而后经过特征提取后,识别待采摘果实,并将识别位置、状态等反馈机器人,由机器人发射采摘命令进行采摘。
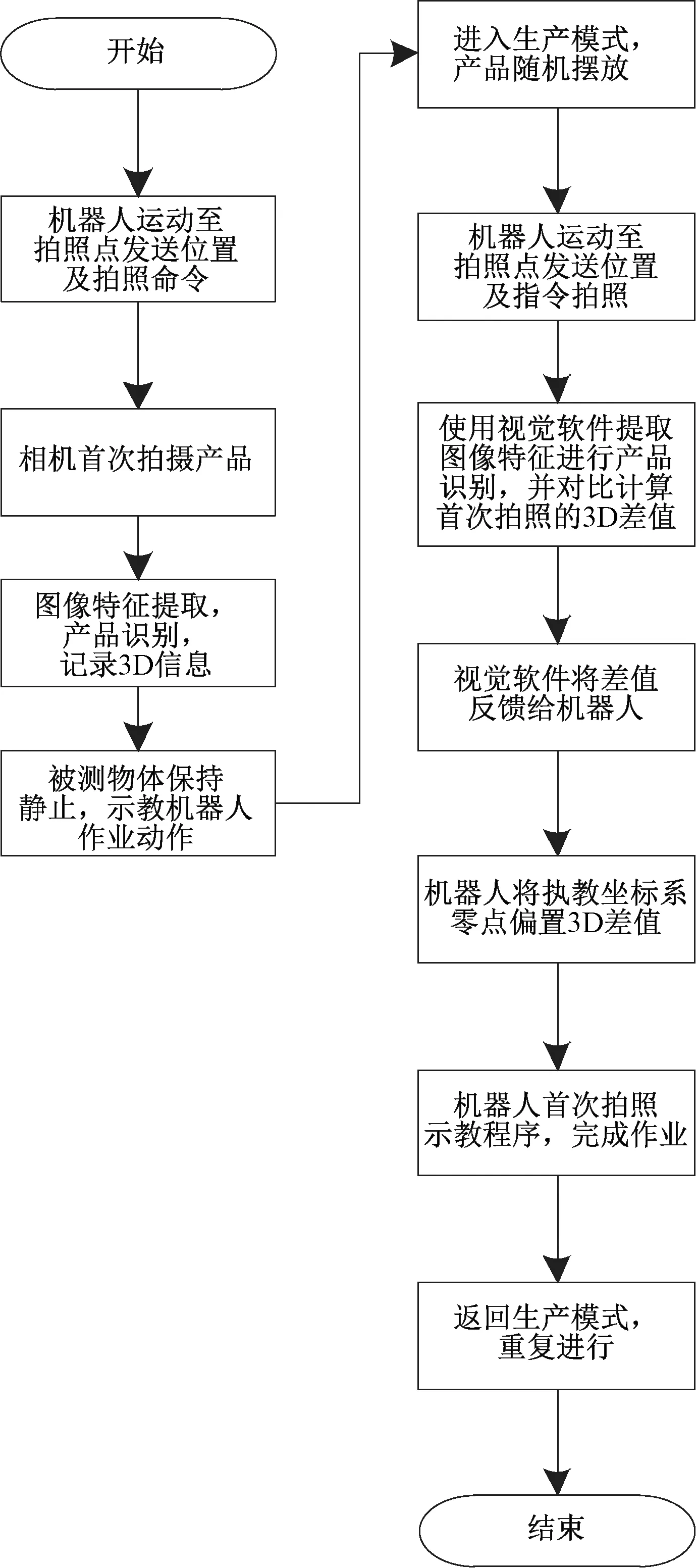
图9 识别算法流程图
然而,这种算法无法识别带有叶子的图像中的水果,因为水果的颜色几乎与叶子的颜色相同[8]。为了从叶子中识别水果,这个系统需要对辣椒进行强光照明[9]。果实的灰度值与叶子的灰度值不同,如图10所示。只有甜椒部分可以被图像中的算法和照明识别效果。

3.3 定位和采摘装置
摄像机的定位系统控制框架的三个制动器,该制动器具有采摘装置和摄像机并使用视觉反馈控制。视觉反馈控制的框图的系统操作如下:首先两个CCD摄像机四处移动,捕捉彩色图像,因为两个图像上都能识别出甜椒的果实。水果被捕获后,水果的中心与参考中心对齐。最后从两个识别水果图像的中心位置计算深度位置,并在深度方向驱动帧直到参考深度位置。目标块的x轴取值范围在iN~(imin+5,imax+5),y轴取值范围在jN~(jmin+5,jmax+5)。其相对应的(p+q)阶矩可以定义为:
然后利用一阶矩M10、M01除以零阶矩阵M00,获取物体的质心坐标。
采摘装置设置在平移连杆上,该平移连杆由齿条和小齿轮驱动,在相机定位到识别的胡椒之后,链接延伸并且将采摘装置接近胡椒并采摘它。

4 运动控制实验
该实验在两种情况下进行,一个是对黄色的甜椒进行采摘如图11(a),另外一个是对绿色的甜椒进行采摘如图11(b)。重点测试光源以及彩椒的颜色对于采摘率的影响,在温室大鹏内加光源后,天气晴朗的白天,进行机器人采摘实验。经过实验发现,加入光源后对于黄色甜椒的采摘成功率高于绿色彩椒,采摘成功率接近98%,但是对于绿色采摘成功率仅为92%。不加光源,采摘机器人对于绿色甜椒与黄色甜椒的采摘率不相上下,采摘率均达到了98%以上。但是在阴雨的白天和晚上采摘成功率均高于天晴时的白天,阴雨天的采摘率平均为95%,高于晴天的93%。
在叶子实验中,如图所示的所有甜椒都可以被识别。该研究结果为智能甜椒采摘机器人的开发研究提供了技术参考。
5 结论
研制一种温室园艺甜椒采摘机器人,同时构建了该采摘机器人的运动学模型。虽然正运动学问题的解是稳定的正解,但逆运动学问题的解严格依赖于机器人的结构。这里有一些在驱动反向运动学时应该考虑的困难。对研制的原型机器人的功能和各部分进行了说明,并给出了实验结果。功能大致分为甜椒果实识别系统和采摘系统,机器人有识别系统和采摘系统。在识别系统中,使用了带有照明和立体视觉图像处理技术。开发的摄像机定位系统具备视觉反馈控制功能,其上装设了采摘装置。同时针对黄色和绿色的甜椒进行实验并成功识别,重点识别了有无光源以及彩椒颜色对于采摘率的影响,实验结果显示,机器人在有光源的情况下,对于黄色甜椒的采摘率高于绿色甜椒;无光源的情况下,二者基本一致。同时,光源阴雨天的成功率明显高于天气晴朗的白天。而果率识别能力的提高和采摘系统将在未来的研究中进行研究。

