基于多方法的煤层底板突水危险性评价

任君豪 ，王心义 ,2,3，王 麒 ，王俊智 ，张 波 ，郭水涛

(1.河南理工大学 资源环境学院，河南 焦作 454003；2.中原经济区煤层(页岩)气河南协同创新中心，河南焦作 454003；3.煤炭安全生产与清洁高效利用省部共建协同创新中心，河南 焦作 454003；4.华北水利水电大学 地球科学与工程学院，河南 郑州 450045；5.上海亚新建设工程有限公司，上海 201900；6.中国平煤神马集团能源化工研究院，河南 平顶山 467000；7.河南焦煤能源有限公司，河南 焦作 454100)

我国具有较为丰富的化石能源，其中煤炭资源占已探明化石能源的94.3%，地下开采的原煤量占煤炭产量的90%[1]。“富煤、贫油、缺气”的资源禀赋状况，决定了今后相当长一个时期内煤炭依然是国家能源生产与消费的主体[2]。华北型煤田主采石炭二叠纪煤层，随着开采深度逐渐加大，断层和褶皱等地质构造的发育，以及隔水层单薄且采动下容易破裂，下伏高水压和强富水的灰岩含水层威胁日益严重[3]。如何客观准确地评价煤层底板突水危险性以采取针对性强的防治水对策，是保障矿井安全生产的基础。

煤层底板突水危险性评价是一项涉及构造地质、煤炭地质、水文地质、工程地质、地质力学、采矿工程、数学地质和地理信息系统等学科的工作，国内外众多专家学者围绕这一多因素决策问题，开展现场监测、室内实验、理论分析、计算机模拟、实践应用等方面的研究工作。20 世纪90 年代初，在煤层底板突水和水害防治方面，我国学者提出了诸多理论，如“下三带”理论、“下四带”理论、“原位张裂与零位破坏”理论、“关键层”理论、“岩水应力关系”理论、“强渗通道”理论等。除以上理论研究，诸多学者针对不同的研究对象，利用不同的指标因子，应用不同的数学方法进行了煤层底板突水评价，形成的方法有突水系数法[4]、脆弱性指数法[5]、神经网络法[6]、模糊数学法[7]、灰色系统理论法[8]、五图双系数法[9]、主控指标法[10]等。突水系数法以其公式明晰、计算简单、需要指标少且容易监测而成为《煤矿防治水细则》的规定用法。Zeng Yifan 等[11]在分析确定煤层底板突水主控因素的基础上，基于GIS 及AHP 法估算各因素的影响权重，制定煤层的脆弱性分区图，建立突水评价模型。Wang Xintong等[12]分析了王楼矿的地质构造、水文地质条件、底板隔水状态和开采条件，基于非线性模糊数学法和层次分析法，提出了煤矿底板突水危险性的非线性模糊区间评价方法，包括多指标评价体系和计算模型。Hu Yanbo 等[13]综合层次分析法和熵权法，对研究区煤层进行了底板突水危险性评价。靳德武等[14]结合物探手段与深度学习理论，构建了煤层底板水害三维监测与智能预警系统，为我国华北型煤田煤层底板水害监测预警提供了新的技术与装备支撑。

总之，国内外关于煤层底板突水机理及预测预警的研究成果较丰富，形成的多种理论和众多评价方法已用于指导矿井底板水害的防治。但目前存在的主要问题是，即使同一矿井的同样数据，采用不同的评价方法其评价结果存在较大差异。因此，开展多方法比对分析研究对于精准评价煤层底板突水危险性具有重要意义。

本文以平顶山煤田(以下简称平煤)相邻的二矿、十矿和十二矿为研究对象，以隔水层厚度、断层复杂程度、含水层水压、含水层单位涌水量、采高等为评价因子，分别利用物元可拓、模糊可变集、突变理论、模糊综合评判4 种方法，对煤层底板突水危险性进行评价，基于专门构建的误差模型比对分析多方法的评价结果，遴选适宜的评价方法，并在此基础上划分带压开采的底板突水危险性分区，以期为平煤区煤矿防治水工作提供参考。

1 指标因子遴选及权重

1.1 研究区概况

平煤主要开采二叠系山西组己组煤和石炭系太原组庚组煤，煤层底板的寒武系石灰岩为岩溶发育不均一和富水性不均衡的含水层，因补给较充沛且含水层厚度大，水压较高，是威胁矿井采掘的主要充水水源。目前，二矿开采庚组煤，十矿和十二矿开采己组煤，其带压区域分布如图1 所示，综合柱状如图2 所示。

图1 平煤3 矿带压开采区分布Fig.1 Distribution of the mining area under pressure in three coal mines of Pingdingshan Coalfield

图2 研究区综合柱状图Fig.2 Comprehensive drill log of the study area

1.2 指标因子遴选

针对本研究对象拥有资料的情况和采掘实际，选用隔水层厚度、断层复杂程度、含水层水压、含水层单位涌水量、采高作为评价因子。

隔水层厚度指煤层底板与含水层顶板之间的距离，隔水层越厚，底板岩体抵抗突水的性能越好。断层是煤层底板突水的主要导水通道，断层复杂程度越高，发生突水的可能性越高。含水层水压是底板突水的驱动力和前提。单位涌水量反映含水层含水介质的渗透性强弱及补给条件的良好程度。采高影响着采掘活动造成的顶底板岩体破坏程度。评价指标体系如图3所示。

图3 突水危险性评价指标Fig.3 Risk assessment index of water inrush

1.3 指标因子赋值

目前，断层复杂程度常用分形理论[15-16]来评价，分形维数值越大断层复杂程度越高。本文收集的51 个钻孔处寒武系灰岩含水层的水压、单位涌水量、隔水层厚度、采高及计算的断层分维值见表1。

表1 指标因子赋值结果Table 1 Quantitative results of index factors

1.4 指标因子权重

针对指标因子xij，可分别利用层次分析法[17]和灰色关联分析法[18]计算各指标常权权重。为克服单一方法确定权重的局限性，应用最小相对信息熵原理[19]建立优化组合赋权模型以确定复合权重其计算公式为：

求得复合常权权重后，根据变权理论[20]可计算指标因子的变权权重。计算公式为：

式中：i为样本数，i=1,2,···,51；j为指标数，j=1,2,···,5；为指标常权权重；ωij为某样本指标变权权重；c、a1、a2、a3为调权参数；dj1、dj2、dj3为指标变权区间阈值；xij为某样本指标因子量化值。

首先确定式(3)中的调权参数，利用K-均值聚类法将各评价指标因子数据分成4 个类别，确定指标因子临界值，取相邻2 个临界值的均值作为指标因子的变权区间阈值dj1、dj2、dj3，其变权区间见表2。

表2 各指标对应的变权区间Table 2 Variable weight intervals of each index

根据九标度层次分析法和灰色关联分析法，分别计算出各指标因子的主观权重ω1=(0.325 4,0.171 8,0.306 4,0.109 3,0.087 0)和客观权重ω2=(0.225 4,0.185 4,0.219 2,0.185 0,0.185 0)，按照式(1)得到组合权重ω0。

钻孔2-9 归一后的水压、单位涌水量、采高、隔水层厚度、断层分维值为x=(0.096 0,0.783 4,0.242 4,0.576 9,0.573 8)，据表2 计算结果，其指标因子量化值分别位于惩罚区间、初激励区间、不激励不惩罚区间、强激励区间、初激励区间。再次利用层次分析法及专家打分法，确定其理想变权权重ω=(0.210 0,0.197 4,0.142 7,0.290 0,0.159 9)，将x、ω0与ω代入式(2)和式(3)，联立方程并利用Matlab 软件可解得c=0.989 9，a1=–3.024 3，a2=0.299 1，a3=0.396 7，确定式(3)中的调权参数。

以钻孔2-1 为例，归一化后的指标值x=(0.042 1,0.153 2,0.205 3,0.849 7,0.437 6)，依据表2 将x代入式(3)，计算状态变权向量S(X)=(0.176 2,0.146 5,0.141 3,0.357 6,0.145 5)，再 将S(X) 和 常 权 向 量ω0代 入式(2)，得到钻孔2-1 的变权权重为ω2-1=(0.182 2,0.151 5,0.146 1,0.369 8,0.150 5)。重复以上步骤，对矿井所有钻孔的变权权重进行计算。

2 突水危险性评价

2.1 物元可拓法

基于K-均值聚类分析结果，将煤层底板突水危险性划分为4 个等级，级别越高突水危险性越大，即Mi={Ⅰ级，Ⅱ级，Ⅲ级，Ⅳ级}={安全区，低威胁区，高威胁区，危险区}。

对指标因子量化值进行归一化处理，并根据物元可拓理论[21]构建对应于4 个突水危险性等级经典域Rj(j=1,2,3,4)、节域Rp和待评物元R0。经典域指各指标对应4 个等级的区间，根据表2，其经典域为：

节域即指标量化值的变化范围，经过归一化处理后为：

待评物元指某钻孔的各指标量化值，针对钻孔10-1，其待评物元为：

基于5 个指标因子的变权权重和待评物元矩阵，按照物元可拓模型可求得钻孔10-1 对应于4 个等级的贴近度为：

选择贴近度最高值为评价结果，即钻孔10-1 处的煤层底板突水危险性为等级Ⅱ，属于低威胁区。

2.2 模糊可变集理论

根据模糊可变集理论[22]，每个等级区间由“吸引域”及“排斥域”组成，“吸引域”[a,b]为表2 中各等级上下界，“排斥域”[c,d]中的c为上一等级的区间下界，d为下一等级的区间上界，M为[a,b]区间中点值。基于K-均值聚类分析结果，5 个评价因子对应于4 个等级的识别区间[c,d]、[a,b]，区间中点值M以矩阵Iab、Icd、IM表达如下：

依据钻孔10-1 五个评价因子的实际值和[c,d]、[a,b]及M的位置关系，计算得到相对隶属度矩阵μA(u)[23]：

将相对隶属度矩阵μA(u)与对应的变权权重复合运算，求到综合相对隶属度。再将综合相对隶属度归一化处理，分别与相对应的等级相乘并求和，得到级别特征值H。不同参数组合下的级别特征值及均值见表3。

表3 不同参数条件下的计算结果Table 3 Calculation results under different parameter conditions

根据研究区的实际情况并参照相关研究成果[24]，利用级别特征值H划定的煤层底板突水危险性分级标准为：Ⅰ级，H<1.5 为安全区；Ⅱ级，1.5≤H<2.5 为低威胁区；Ⅲ级，2.5≤H<3.5 为高威胁区；Ⅳ级，3.5≤H<4.5 为危险区。基于此确定10-1 钻孔处底板突水危险性属于低威胁区，即为等级Ⅱ。

2.3 突变理论

隶属函数的确定是突变理论[25]综合评价至关重要的环节，确定隶属函数的方法有多种，总体上可分为专家确定法、借用已有“客观”尺度法、模糊统计法、对比排序法、综合加权法、基本概念扩充法等6 类。这里采用模糊统计法中的梯形模糊隶属函数C(x)，结合均值−均方差法确定参数α和β。

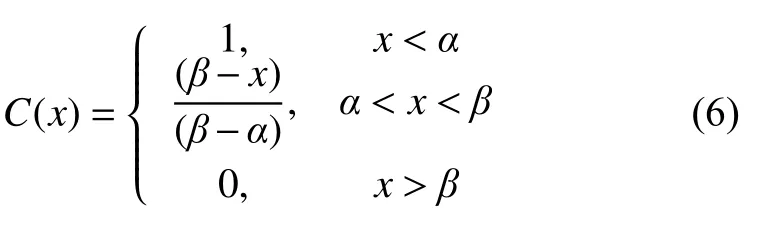
常见的突变类型有折叠突变、尖点突变、燕尾突变、蝴蝶突变等，本文根据控制变量的个数，引入折叠型突变与尖点型突变进行分析。以钻孔10-1 为例，具体计算结果见表4。

表4 突水危险性评价指标及结果Table 4 Water inrush risk assessment indexes and results

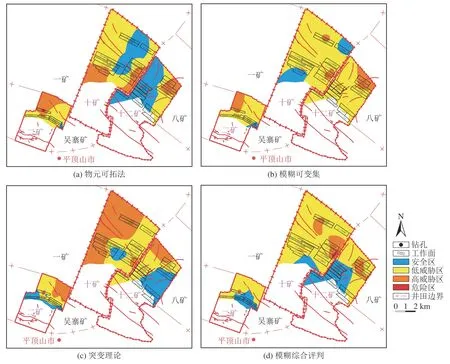
参考国内外研究成果[26]，定义突变理论综合评价的等级划分标准为：Ⅰ级，0.9

2.4 模糊综合评判法

模糊综合评判法是[27]一种使模糊不清的评价因子有效量化的常规方法。基于K-均值聚类分析结果，设定底板突水威胁性模糊综合评价集V={Ⅰ级，Ⅱ级，Ⅲ级，Ⅳ级}={安全区，低威胁区，高威胁区，危险区}，然后将5 个评价因子代入隶属度函数γ(x)：

得到模糊矩阵F，针对钻孔10-1 有：

利用加权平均型算子，进行模糊矩阵F和权重ω矩阵的复合运算，得到区间隶属度向量B：

根据最大隶属度原则确定模糊综合评价模型的评价等级。显然，钻孔10-1 属于等级Ⅰ，即为低威胁区。

3 评价方法比对分析

3.1 评价结果

利用上述4 种方法可评价51 个钻孔处的煤层底板突水危险性，其中Ⅰ级为安全区、Ⅱ级为低威胁区、Ⅲ级为高威胁区、Ⅳ级为危险区，结果列于表5，对应的煤层底板突水危险性分区如图4 所示。

表5 不同方法的底板突水危险性评价结果Table 5 Risk assessment results by different methods

3.2 比对分析

平煤二矿开采石炭系太原组庚组煤，煤层底板隔水层平均厚度为24.1 m，31 采区工作面平均宽度为180 m，按照《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》[28]建议的底板扰动破坏深度公式：

式中：h为底板扰动破坏深度，m；L为工作面宽度，m。

计算可得二矿31 采区底板扰动破坏深度最大为20.12 m，二矿庚组煤有效隔水层厚度见表6。

由表6 可以看出，庚-31060 工作面附近6 个钻孔的有效隔水层厚度均小于0，底板扰动破坏裂隙可能会直接沟通下伏寒武系崮山组厚层灰岩含水层，其发生底板突水的可能性极高，即突水危险性应在高威胁区以上。模糊综合评判的评价结果中，庚-31060 工作面高威胁区面积占比仅12.6%，低威胁区和安全区面积占比为87.4%，较实际情况明显偏低，说明该方法不适用于二矿。

表6 二矿有效隔水层厚度Table 6 Effective aquiclude thickness of No.2 Coal Mine

十矿己三采区北部的己-33200 工作面回采至中部地段时，曾发生水量160 m3/h 的底板寒武系灰岩含水层涌水，对工作面回采造成了较大的影响。而物元可拓法将该工作面中部以东地段定义为安全区，出现了较严重的误判，说明该方法并不适用十矿。

由表1 钻孔可以看出，十二矿平均水压为十矿的1.74 倍，而平均隔水层厚度仅为十矿的1.10 倍，且十二矿构造较十矿更为发育，理论上十二矿的突水危险性高于十矿。但突变理论界定的十二矿安全区面积占比37.9%，十矿安全区面积占比仅为4.43%，十二矿安全区面积占比远大于十矿，说明突变理论的评价结果偏离实际，本方法不适用于十二矿。

综上所述，4 种方法中模糊可变集的评价结果与实际情况最为吻合。该方法合理判断了二矿及十二矿的高突水威胁性，对涌水的十矿己-33200 工作面也做出了精准的预测。模糊可变集法为平煤二矿、十矿、十二矿煤层底板突水危险性评价最为适宜的方法，其评价结果的分区情况如图4b 所示，分区面积及其占比见表7。

表7 分区面积及其所占带压区比例Table 7 Zoning areas and the proportions in the pressure zones

图4 不同评价方法的分区结果Fig.4 Zoning results of different evaluation methods

突变理论的分级结果偏低，可以推测是突变理论低估了部分指标的影响程度。模糊综合评判法及物元可拓法的分级结果偏低，原因可能是指标分区不够精确，导致对较大指标的相对隶属度计算偏小。模糊可变集理论基于“吸引域”及“排斥域”确定指标分区阈值，指标分区结果较物元可拓法、模糊综合评判法更精细，相对隶属度计算中优化准则参数k与距离参数P的不同组合，可以更合理地表征指标因子与煤层底板突水之间复杂的非线性关系。

4 结论

a.遴选隔水层厚度、断层复杂程度、含水层水压、含水层单位涌水量、采高为指标因子，应用变权理论确定了各指标因子的权重，分别利用物元可拓法、模糊可变集理论、突变理论和模糊综合评判法评价了平煤二矿、十矿和十二矿煤层底板突水危险性，并划分了突水危险性等级。

b.对比实际开采情况，模糊可变集理论的评价结果与实际情况最为吻合，该方法对安全区、低威胁区的识别更准确，合理判断了二矿及十二矿的高突水威胁性，对涌水的十矿己-33200 工作面也做出了精准的预测，是最适宜研究区的底板突水危险性评价方法。

c.相较于物元可拓法、突变理论、模糊综合评判法，模糊可变集理论的指标分区构建及隶属度计算更为精细合理，更好地表征了指标因子与煤层底板突水之间复杂的非线性关系，评价结果较符合实际情况，对矿井采掘时采取针对性强的防治水对策具有一定价值。

d.模糊可变集理论评价结果表明，二矿、十矿、十二矿带压区内安全区占比分别为4.08%、14.30%、0，低威胁区占比分别为76.91%、83.14%、85.78%，高威胁区占比分别为19.01%、2.56%、14.22%，研究区内暂无危险区。