基于BP神经网络的直升机飞行状态识别

高健桐

(中国直升机设计研究所，江西 景德镇 333001)

0 引言

直升机因其良好的机动性能，可以适应不同的环境，在民用领域及军事领域得到了普遍运用。但直升机具有灵活机动的特点，其飞行状态具有多样性。在不同飞行状态时，直升机动部件和有寿件承载的载荷复杂多变，容易造成损伤差异。因此，正确识别飞行状态对直升机关键部件的寿命预测及故障诊断具有重要的意义。

直升机飞行状态识别方法不断更新和发展，识别方法主要划分为动力学法、图像分析法及神经网络法。Weiss 等提出通过结合垂直变化、姿态角度和动力学构建数学模型，利用该模型的功率谱来识别直升机飞行姿态的方法，但该方法只是对悬停状态进行了研究，对其他的飞行状态还缺乏理论支撑。张祖勋等利用序列影像实现飞行状态识别，该方法虽然在理想的飞行姿态模型中取得了较好的成效，但是并不适用于其他飞行姿态。李军亮等将 Elman神经网络应用于直升机飞行状态识别，虽然取得了较好的效果，但是该方法的输入维数较高，导致网络模型难以收敛，另外在小样本情况下的识别正确率不高。在实际中，由于采集的飞行参数数据较少，用于网络训练的往往是小样本，因此，还需要进一步研究小样本下的高性能的直升机飞行状态识别方法。

本文以指示空速数据为示例，分析数据特性，运用线性拟合和逻辑判断方法展开研究，并进行稳定数据段分割。随后将分割好的数据段代入搭建的BP神经网络进行“水平”、“上升”、“下降”三种曲线趋势的模式识别。

1 数据稳定段区域判断

本文以随机性较大、波动较为明显的指示空速展开判断示例数据分析。

1.1 线性拟合配合逻辑判断

一般来说，飞参的采样频率不会像振动、噪声的采样频率那么高。以某次飞参采集数据为例，采样频率为16 Hz。根据奈奎斯特定理可知，当采样频率大于信号中最高频率的2倍时，采样之后的数字信号会完整地保留原始信号的信息。而以飞参数据为例，采样频率为16 Hz，则仅能分析原始信号8 Hz以内的频率特征信息。受限于采样频率，采集到的数据频域特征不明显，常规的频谱分析、小波变化等方法用于前期的数据预处理的效果并不理想。本文利用数学线性拟合配合逻辑判断的方法来对数据进行分割。线性拟合曲线的方法具备一定的对抗数据波动和噪声干扰的能力。

分别对采样点前后秒数据小段进行线性拟合，得到拟合曲线的斜率和。设定一个阈值进行以下逻辑判断，形成稳定性判断输出函数。

=1,|-|<

(1)

=0,|-|>

(2)

图1列举出了一种形式的示例数据及其按照上述方法形成的稳定性判断函数。根据稳定性判断输出函数形成时间状态分割点。这里做出假设，即每一阶段的稳定数据结束后，发生变化，然后进入到另一个稳定状态阶段。按照上述假设选取相邻的稳定状态分界点的对应时刻，取中值点处理，输出结果如表1所示。

图1 示例数据图及稳定性判断结果

表1 示例数据稳定状态分割点

1.2 指示空速稳定性判断

本文以指示空速数据作为处理数据的示例。因为用于飞行状态识别的数据精度要求并不是很高，一般1 s对应一个速度点是可以满足精度要求的，所以对数据进行重采样处理，将原采样的16 Hz重采样为1 Hz。选取形成的指示空速数据如图2所示。

图2 指示空速飞参数据

进行上述线性拟合逻辑判断形成的数据分割结果为如图3所示结果。

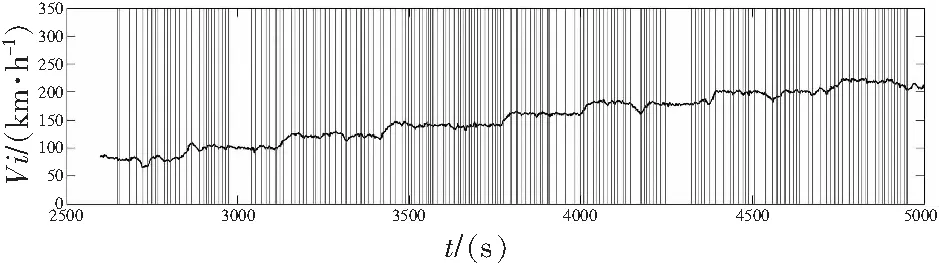
图3 指示空速飞稳定性分割结果

从分割结果可以看出，数据分割点较为密集。这种分割结果不利于飞行状态识别，也不符合人工视觉判断逻辑，需要在上述处理得到的结果基础上进行进一步处理。本文采取了曲线拟合、均值处理和稳定性判断的方法，循环了4次稳定性判断，最终得到的分割结果如图4和图5所示。

图4 4次稳定性判断结果

图5 经过4次稳定性判断后指示空速飞稳定性分割结果

循环算法基于以下原则：

当稳定性判断结果为1时，选取区域段数据进行均值处理；

当稳定性判断结果为0时，选取区域段数据进行线性拟合；

将上述处理后结果重新拼接起来，采取新的′ 秒判读数据和阈值′，重新执行稳定性判断程序。

依次进行循环，当前后两次稳定性判断结果输出相差小于005时，则停止循环，输出稳定性判断输出结果。

2 搭建BP神经网络

2.1 BP神经网络理论

BP神经网络(Back Propagation)是一种神经网络学习算法。BP神经网络主要由输入层、隐含层和输出层组成，如图6所示。

图6 BP神经网络示意图[4]

BP网络设计一般从网络层数、各阶层神经元数和各阶层间传递函数等几方面考虑。网络层数的设定会直接影响识别精度和网络训练时间，较为常用的BP神经网络就是三层结构，即包含一个输入层、一个输出层和一个隐含层。输入层神经元个数和输出层神经元个数分别跟输入维数和输出维数相同。隐含层神经元个数可以按照Kolmogorve经验公式进行参考选择，如式(3)所示。

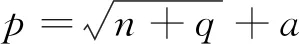
(3)

其中，为隐含层神经元个数；为输入层神经元个数；为输出层神经元格式；为0～1之间的常数。

BP神经网络输出层的传递函数可以选用S型函数或线性函数两种形式，选用S型函数会对网络输出值进行0～1的限制，选用线性函数则不会对网络输出值有限制。隐含层通常采用S型函数作为传递函数，可以使得网络学习具有非线性特性。

2.2 建立训练样本

本文按照“水平”、“上升”、“下降”趋势进行数值数据库训练样本的建立。训练样本主要考虑了不同初值、不同斜率、不同噪声影响的条件下进行数值模型建立。

按照式(4)建立带有噪声干扰的模拟水平飞参数据，以数值1为水平基准，增加不同大小的随机噪声组成。共建立120组水平直线样本数据库。

()=1+*()

(=01、02、03……)

(4)

按照式(5)建立带有噪声干扰的模拟上升飞参数据，选取不同的斜率，增加不同大小的随机噪声组成。共建立240组上升直线样本数据库。

()=*+*()

(=05、1、2、3……)

(5)

按照式(6)建立带有噪声干扰的模拟下降飞参数据，选取不同的斜率，增加不同大小的随机噪声组成。共建立240组下降直线样本数据库。

()=*+*()

(=-05、-1、-2……)

(6)

2.3 搭建BP神经网络

本文考虑了“水平”、“上升”、“下降”三种时域信号的趋势状态，输入神经元设定为60。输出模式的标准向量为(0 0 1)、(0 1 0)和(1 0 0)，分别对应着“水平”、“上升”、“下降”3种时域信号的趋势状态，输出层神经元为3。输出向量的元素为0～1的值，因此输出层神经元的传递函数为S型对数函数log sig。采用单隐层元的BP网络，参考Kolmogorve经验公式，设定隐含层神经元个数为18，隐含层神经元的传递函数为S型正切函数tan sig。选取学习速率为0.05，以600组数值模拟数据作为样本数据，建立一个60-18-3的BP神经网络。将分割好的数据段代入建立好的神经网络，进行模式识别输出。

3 平飞试验数据识别

3.1 平飞试验数据处理

选取时长大约40 min的部分平飞数据，将各参数按照上述方法进行分割，状态分割结果如图7所示。从目测的分割情况来看，分割效果较为符合人工分割习惯。

图7 平飞试飞测试数据及状态分割结果

3.2 识别结果

采取多参数叠加分割的办法进行飞行状态识别。将各参数每段数据带入上述建立的神经网络，并在此基础上增加逻辑判断，则以上截取的数据输出如表2所示。

表2 平飞试飞测试数据飞行状态识别结果及人工评判结果

4 结论

本文结合稳定状态时间段分割和BP神经网络方法进行直升机飞行状态识别。以40 min的平飞数据作为示例，用线性拟合和逻辑判断的方法对各参数稳定性进行判断并依此进行稳定状态时间点分割。将分割的各时间段带入建立好的神经网络，输出得到状态识别结果。得出以下结论：

1)结合线性拟合和逻辑判断方法，可以对时域信号变化特征较明显的信号进行稳定状态分割；

2)当分析数据较为复杂时，只采用上述方法会导致分割效果较差，可以通过对分割信号进行线性拟合和均值处理的方法，循环进行稳定性判断，得到较符合逻辑的分割结果；

3)将完成分割的时间段各参数带入BP神经网络可以应用于飞行状态的模式识别，以本文的示例为例，识别结果与人工判断结果检验无误。