阻尼网控制圆柱流动和噪声的计算研究
朱文庆,仲唯贵
(中国直升机设计研究所,江西 景德镇 333001)
0 引言
直升机在大速度前飞时包含了大量的类圆柱流动,例如起落架的轮子、支柱,桨毂雷达,主减塔座,排气管等。这些部件自身的气流分离和尾迹及其与下游部件的干涉形成明显的振动,如直升机中常见的尾筛现象就是由主减塔座、尾气管等上游脱落涡与垂尾干涉形成的。起落架中的类圆柱流动还会形成显著的噪声辐射,如大型的商用固定翼飞机中,降落状态时起落架噪声占总噪声的比重达40%。大型直升机也具有较大尺寸的起落架,如米-26主起落架直径达1.12 m,在大速度前飞时,起落架也会产生显著的振动和噪声。事实上,直升机起落架的噪声已得到相关学者的关注。
阻尼网作为流动控制装置已在风洞中得到广泛的应用,近年来,其噪声控制效果也得到了大量的试验试飞的验证。欧盟和日本均启动了飞行试验项目来验证阻尼网的降噪效果。在欧盟的SILENCE(Significantly Lower Community Exposure to Aircraft Noise)项目中,使用阻尼网代替整流罩以减弱对附近流体的加速和转向,降低了起落架的感受性噪声1.8 dB。日本的FQUROH(Flight demonstration of QUiet technology to Reduce nOise from High-lift configurations)项目中,通过飞行试验验证了阻尼网降噪的有效性,在90°辐射方向上,总声压级降低为4.2~4.4 dB。
实际上,航空器中的部件外形复杂,不利于机理层面的研究。为此,相关学者以圆柱、工字梁等简化模型为对象,开展了阻尼网对噪声的控制研究。Boorsma等以单圆柱和工字梁为研究对象,探索了不同开孔率的阻尼网对噪声的影响规律。Oerlemans等研究了阻尼网几何参数对降噪的影响,横向的椭圆形阻尼网具有最好的降噪效果,能降低中低频噪声25 dB,使之到达背景噪声的水平。
为研究更多的流动细节,增进对阻尼网控制流动和噪声的理解,近年来,对阻尼网的数值模拟研究不断涌现。Murayama等对安装阻尼网的主起落架进行了数值模拟,计算中解析了阻尼网的几何外形。在FQUROH项目中,Murayama等又对“Hisho”验证机的主起落架进行了数值模拟,计算重现了风洞试验和飞行试验中的控制结果,但计算网格量达到了2.5亿左右。
阻尼网复杂多尺度的外形对直接解析方法造成了巨大的挑战。为提高计算效率,Okolo等在流场中阻尼网所在位置设置虚拟区域,在该区域上添加体积力源项来代替阻尼网的作用,但并未对模化方法和流场改变做详细描述,也缺乏严谨的验证工作和机理探讨。朱文庆等对该方法做了进一步的发展和验证。
本文的主要目的是采用阻尼网数值模型研究阻尼网在圆柱绕流中对流动和噪声的控制机理和控制规律,为阻尼网在直升机流动控制中的应用奠定理论基础。
1 数值方法
1.1 阻尼网模型
本文采用由朱文庆等开发的数值模型。在该模型中,阻尼网对流动的影响分为4项:流动阻力,速度折射,对来流湍流的衰减和自身湍流的产生。本文的阻尼网放置在圆柱之前,不需要考虑对来流湍流的衰减;阻尼网自身产生的湍流具有非常小的尺度,在本文中可以忽略。故本文的阻尼网模型只考虑流动阻力和速度折射。
1.1.1 流动阻力
本文的阻尼网主要应用于直升机中,此时飞行马赫数≈ 0.2。阻尼网的丝线直径在毫米量级。例如,在TIMPAN项目中6个阻尼网的丝线直径在0.1~1.19 mm之间;基于丝线直径的雷诺数范围为400~5000。考虑雷诺数范围,选用Roach公式:
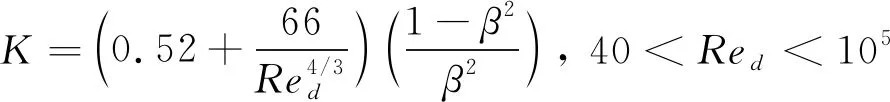
(1)
1.1.2 速度折射
根据已有的文献分析,速度折射依赖于阻力系数和入射角度。TIMPAN项目中用于大量测试的开孔率范围为053~060。根据Boorsma等控制钝体噪声的经验,在入射角度较小时,对流动和噪声的控制效果大;当> 45°时,再增加穿孔区域的面积,对噪声无明显影响。
基于阻尼网的使用工况,选用Gibbing的经验公式:
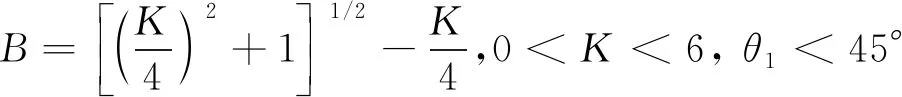
(2)
阻尼网模型要求在阻尼网区域内添加源项来代替阻尼网对流场的作用,如图1所示。
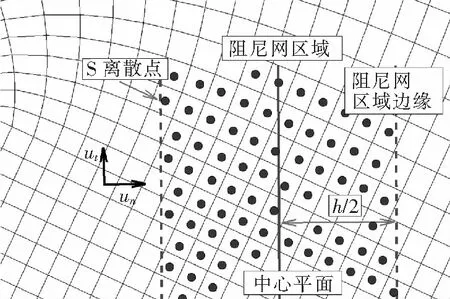
图1 阻尼网实现方式示意图
在阻尼网区域,积分形式的N-S方程写为:
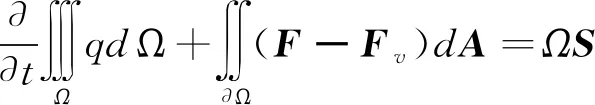
(3)
阻尼网的影响以体积力的形式包含在中:
=[0·]
(4)
为推导的具体形式,此处引入阻尼网当地的法向单位矢量,将到达阻尼网的速度分为法向速度和切向速度:
=(·)
=-
(5)
体积力可表示为:
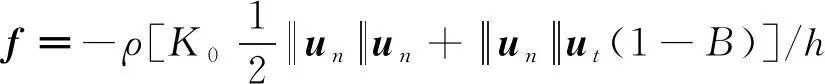
(6)
其中代表阻尼网区域的厚度。在本文中以×代替参与计算,是为了数值稳定性而添加的分布函数,它具有如下形式:
()=2(1-2)
(7)
其中代表距离阻尼网区域中心平面的法向距离。分布函数使得源项更集中在阻尼网区域的中心,有利于降低离散误差,同时也能减小阻尼网区域的有效厚度。
1.2 其他数值方法
本文使用IDDES(Improved Delayed Detach Eddy Simulation)计算声源场的湍流流动。该方法有效结合了带壁面模型的LES和DDES方法的优点,能改善壁面湍流的模拟。计算中无粘通量采用四阶中心和Roe格式的混合格式,并引入自适应耗散函数以降低湍流区的格式耗散。界面通量采用5阶WENO格式重构。粘性通量采用二阶中心格式。在时间推进上,采用带牛顿子迭代LU-SGS方法,能实现二阶计算精度。
使用可穿透的FW-H方程计算噪声的传播。在噪声求解上采用预先时间步方法,即基于声源时间计算接收点的时间,然后用最大二阶的插值方式将声压插值到接收点的时间离散点上。该方法能使流场计算和噪声计算同步进行,避免了大量的声源数据的存储。
2 阻尼网模型的验证
本文采用防风栅算例对阻尼网模型进行验证。该防风栅在外形上与阻尼网极为相似,其试验和计算设置如图2所示。试验中防风栅的高度=100 mm,宽高比为3。该防风栅由3 mm宽的方木条装订而成,木条间距10 mm,开孔率= 0.49,基于木条宽度的雷诺数为1830。

图2 试验和计算设置示意图
计算中来流马赫数为0.1,计算区域与试验相同,从防风栅上游6到下游1396,高度方向为516,展向宽度为102。在防风栅区域,网格尺度为002,总网格量约为65 × 106。本算例中网格不足以解析壁面湍流,故采用定常RANS方法进行计算。本文计算了042和049两个开孔率,以探究开孔率对流场的影响。
图3给出了开孔率为049时平均速度的分布,阻尼网提供了流动的阻力,在其后形成了低速区域。图4则给出了流向和法向速度型与试验的定量对比。开孔率为049时,防风栅前(= -1)和后(= 1,2,4)的速度型与试验值在趋势上相符,但在幅值上存在一定的差距。当开孔率增加到042时,幅值与试验相符。

图3 展向和垂向截面中平均速度的分布(β=0.49)
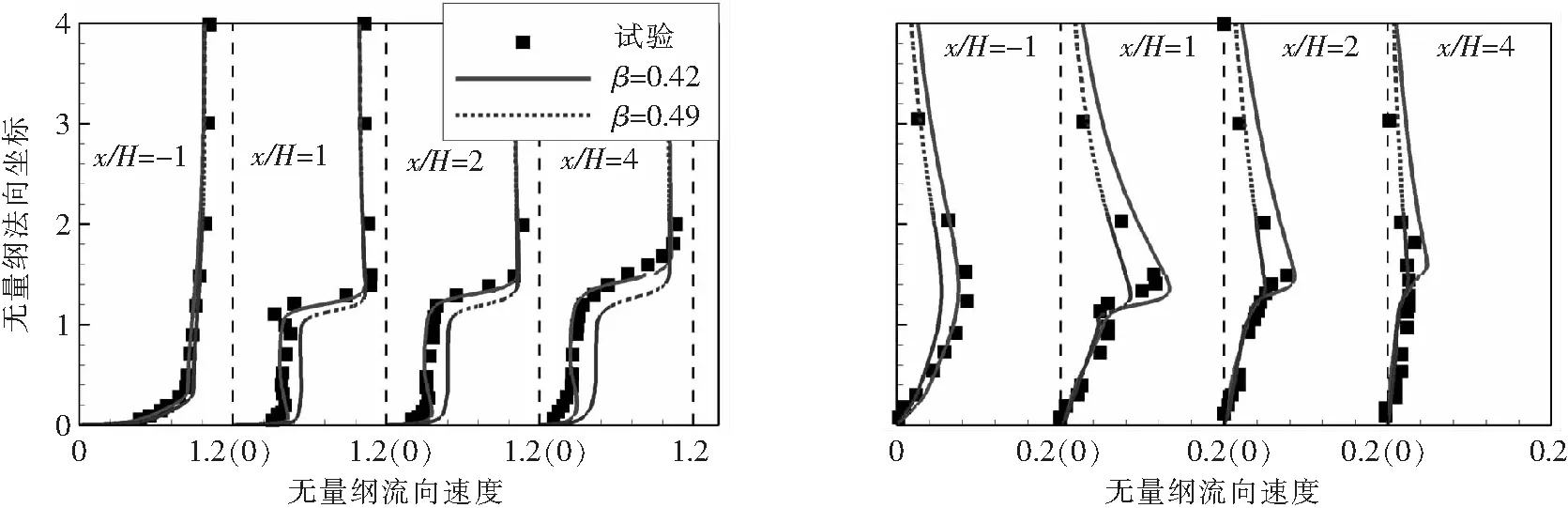
图4 流向和法向速度型与试验的对比
该算例中合适的阻力系数能够得到与试验相符的速度分布,进一步证明了本文计算方法的可靠性。
3 阻尼网控制圆柱的流动和噪声
本文的研究对象为Boorsma等的试验中的单圆柱,直径=100 mm,展向长度=514。试验中使用穿孔板控制圆柱噪声,所使用穿孔板和其安装位置如图5所示。穿孔板直径= 150 mm,穿孔板的厚度为2 mm。该穿孔板只在部分区域开孔,开孔区域的环向范围为[-45°, 45°],前驻点角度为0。本文研究在穿孔区域使用阻尼网对圆柱流动和噪声的控制效果。
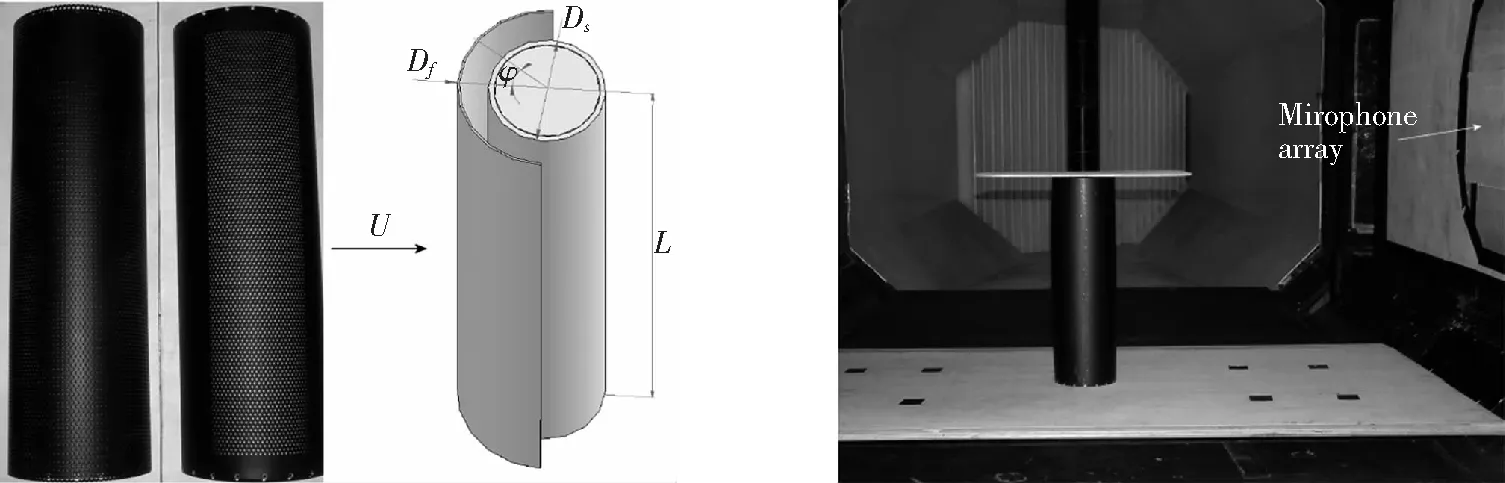
图5 穿孔板及其安装位置示意图[7]
计算中来流=0.2,基于圆柱直径的雷诺数= 2.6×10。圆柱表面和整流罩非开孔区域采用无滑移壁面条件,阻尼网区域采用本文的阻尼网模型。
图6对比了单圆柱,阻尼网开孔率0.42和0.55三个算例的Q等值面。在安装阻尼网的算例中,一部分流体能穿过开孔区域,流向单圆柱;一部分流体将绕过整流罩。整流罩内外的速度差在其尾部形成剪切层。单圆柱和阻尼网开孔率0.42时表现出明显的涡脱特性:单圆柱的涡脱是由其本身的分离涡脱落产生;阻尼网开孔率为0.42时,涡脱则表现为整流罩的分离涡脱落。当开孔率增加到0.55时,不再观察到涡脱现象。

图6 不同算例的Q等值面对比
图7为平均流场的对比,同时也包含了Boorsma等试验中穿孔板开孔率为0.42时的结果。阻尼网增大了圆柱后的分离区,单圆柱尾迹区的再附点位置为1.78,开孔率为042和055时的再附点位置分别为316和41。此外,开孔率为042时,本文计算和Boorsma等的试验具有相似的分离形态。

图7 不同算例平均流场对比(以阻尼网的直径Df为基准进行无量纲化)
图8给出了无量纲流向速度和湍动能沿流向线(=0.0)分布。单圆柱和阻尼网开孔率为0.42时,均表现为典型的圆柱分离特征。如此低开孔率的阻尼网使得整流罩趋向于一个不可穿透的半圆柱,相当于增大了单圆柱的直径,表现为更大的分离区和更高的湍动能峰值。阻尼网开孔率为0.55时,更多的流体流向单圆柱,使得整流罩尾部形成类混合层结构。该混合层极大地增大了分离区,也降低了分离区内速度的不均匀程度和湍动能。
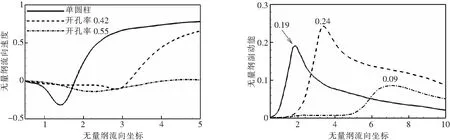
图8 无量纲流向速度和湍动能沿流向线的分布(y/D=0.0)
图9给出了监测点(=265,=-06)处法向速度的功率谱密度。阻尼网开孔率为042时,仍然存在明显的涡脱行为,其无量纲的涡脱频率为019;若以阻尼网直径为无量纲基准,则无量纲频率为0285,符合此雷诺数下圆柱绕流的涡脱特点。阻尼网开孔率055时功率谱密度表现为宽频行为,无涡脱现象。
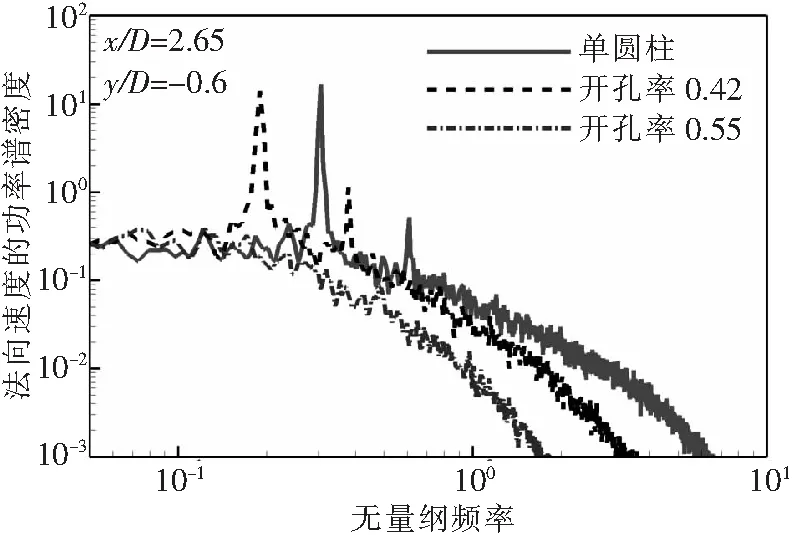
图9 监测点法向速度的功率谱密度
因此,阻尼网能够改变单圆柱的分离区和涡脱特性,从而影响近场的湍流脉动;合适的开孔率能够消除单圆柱的涡脱行为,从而极大地降低湍流脉动。
图10给出了90°辐射角度上远场噪声的功率谱密度,远场麦克风距离圆柱圆心距离=185。作为对比,来自文献的试验结果显示在左图。遗憾的是,文献中没有给出具体的数值。但是,从图中可以看出,在试验中开孔率为0.55时能够抑制主导频率处的噪声;而本文的计算重现了这个控制效果。同时,开孔率0.42时,噪声中存在0.19的无量纲主导频率,该频率处的幅值为71.5 dB,比单圆柱峰值低2.5 dB,但其在中高频率的能量均高于单圆柱噪声。
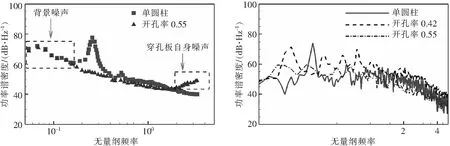
图10 90°辐射角度处噪声功率谱密度的对比
图11给出了三个算例中的总声压级的对比。开孔率为0.55时,阻尼网减小了单圆柱的辐射噪声,在90°方向上的降低量为3.5 dB;而开孔率为0.42时则增大了单圆柱的辐射噪声,相同角度上的增大量为4.1 dB。阻尼网降低单圆柱噪声时需要有合适的开孔率,过小的开孔率反而会使得噪声增加。
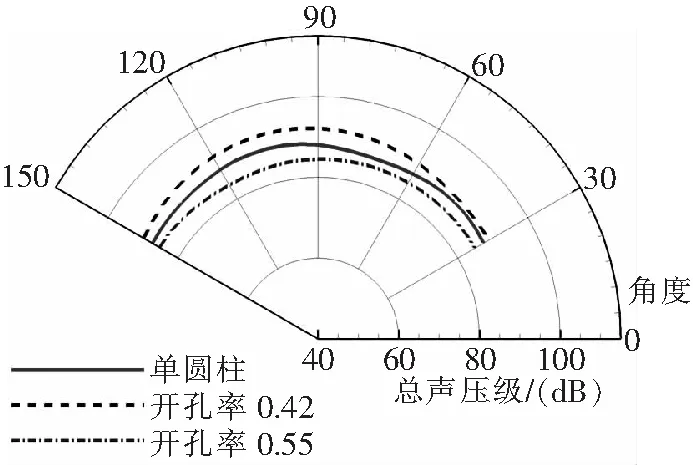
图11 远场总声压级的对比
4 总结
本文探索了阻尼网控制单圆柱振动和噪声辐射的机理,为阻尼网在直升机流动控制中的应用奠定理论基础。计算中流场的模拟采用IDDES方法,远场噪声采用FW-H方程,阻尼网区域采用阻尼网模型。
使用防风栅算例对本文计算方法验证之后,采用开孔率0.42和0.55的两个阻尼网研究其对振动和噪声的控制机理和控制规律。阻尼网通过控制单圆柱的分离区和涡脱特性来影响近场振动和远场噪声。开孔率为0.42时,相当于增大了单圆柱的直径,表现为更大的振动和噪声。开孔率为0.55时,阻尼网降低了单圆柱分离区的不均匀性,消除了涡脱,极大地降低了振动,无量纲湍流脉动最大值从0.19降到0.09。在远场噪声方面,该阻尼网能在90°方向降低总声压级3.5 dB。

