小学生几何操作经验目标制定的原则把握
林晓丹

摘 要:数学基本活动经验主要是学生经历数学活动,感悟归纳、演绎过程中所沉淀下来的思维模式。积累几何操作经验,要让学生亲身经历与内容相关的一些基本活动,从而将抽象的几何变为具体可感知的。而在制定几何操作经验目标时需遵循整体性、层次性、主体性、可行性的原则。
关键词:目标制定;几何操作经验;原则
【中图分类号】G623.5 【文献标识码】A 【文章编号】1005-8877(2022)03-0128-03
The Principles of Setting the Objectives of Primary School Students' Geometry Operation Experience
LIN Xiaodan (Xiamen Minli Second Primary School, Fujian Province, China)
【Abstract】The experience of basic mathematics activities is mainly about students' experience of mathematics activities, and the thinking patterns that have been precipitated in the process of induction and deduction. To accumulate geometric manipulation experience, it is necessary for students to experience some basic activities related to the content in person, so as to turn abstract geometry into concrete and perceptible. The principles of integrity, hierarchy, subjectivity, and feasibility should be followed when formulating geometric operation experience targets.
【Keywords】Objective setting; Geometric operation experience; Principles
“基本活动经验”是在2005年,我国基础教育数学课程改革提出的新术语,它的提出反映了当前数学教育研究新的进展和新的方向,是我国数学教育研究工作深化的体现。2011年《义务教育数学课程标准》在总目标中指出:“通过数学学习,学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验。”由此可见,“基本活动经验”作为“四基”之一,作用不容小觑,积累基本活动经验应该也必须引起教师们的关注。在“图形与几何”领域要关注学生几何操作经验的积累,让学生亲身经历与内容相关的一些基本活动,从而将抽象的几何变为具体可感知的。那怎样的操作是有效的,可以帮助学生积累活动经验?笔者认为,可以从目标的制定上来考量。基于以上的认知,文章就制定几何操作经验目标时需把握哪些原则展开阐述。
1.把握目标制定的整体性原则
2011年《义务教育数学课程标准》将总目标中的“双基”发展为“四基”,这是数学教学目标认识上的飞跃。张奠宙和郑振初曾在《“四基”数学模块教学的构建》一文中指出:“四基”并非孤立地存在着,而是互相链接,形成一个三维的模块。前三基分别构成一个维度,基本数学活动经验本身不构成一个单独维度,而是充填在三维模块中间的黏合剂。由此可见,“四基”不是四部分简单叠加在一起,它们是一个互相促进,相互融合的有机整体。“四基”目标的有效落实,能有效提升学生的数学素养,它不仅是学生当前学习和发展的需要,更是学生未来学习和终身发展的需要。因此,我们在教学设计时,要把握“四基”总目标的整体性原则,要在夯实“双基”的同时,体会和运用数学基本思想方法,不断地积累数学基本活动经验。
而在“图形与几何”领域,不少老师在制定几何操作目标时,侧重学生“双基”目标的达成,忽视基本思想和基本活动验的积累。例如,在教学《长方形和正方形面积计算》时,教师常常把教学目标定位为:知道长方形和正方形的面积计算公式,会应用公式进行计算以及解决一些实际的问题。至于公式是如何推导的,教师并不太关注,原因在于考试不会过多地涉及推导的过程,试卷考查的大多是应用公式進行计算或解决问题。显然,这样忽视目标整体性的落实。笔者在执教这节课时则把精力放在探索面积计算公式上。制定的目标:一是经历长方形、正方形面积公式的推导过程,获得从度量到计算来研究长方形、正方形面积的方法。二是理解长方形、正方形面积公式的意义,掌握长方形、正方形面积计算公式,能运用公式进行长方形和正方形的面积计算,并能解决简单的实际问题。三是在动手操作中体验学习数学的兴趣,在通过自主探究得出结论中体验成功的快乐。让学生在探索公式的学习活动中,首次经历“实验—猜想—验证—结论”研究过程,进而体会数学的严谨以及数学结论的确定性,且将这样的研究模式迁移到后续的学习之中,学生的基本活动经验得到丰富。简单地从考试成绩上来看,两种教法可能差别不大,但是从学生的认知、动手操作和归纳推理能力、数学思考、活动经验积累方面来考查,当然是后者更胜前者。教学以目标为导向,目标是教学的出发点和归宿,把握目标的整体性原则尤为重要。
2.把握目标制定的层次性原则
学生随着年龄的增长,思维能力也逐渐发展,教材的编排也是由浅入深。因此,目标的制定也应遵循层次性的原则。从不同学段相关内容的几何操作目标的横向对比来看。例如,在第一学段“图形的认识”中要求学生能通过实物和模型辨认长方体、正方体、圆柱和球等几何体;能辨认长方形、正方形、三角形、平行四边形、圆形等简单图形。在第二学段“图形的认识”中要求学生通过观察、操作,认识平行四边形、梯形和圆,知道扇形,会用圆规画圆;学生通过观察、操作,认识长方体、正方体、圆柱和圆锥,认识长方体、正方体、圆柱的展开图。行为动词从“辨认”—“初步认识”—“认识”,很显然,层层递进,体现了生活现实到数学概括,从整体到局部特点,且“三维—二维—三维”交替出现,目标的要求逐渐提高。
从不同学段知识之间的纵向联系来看,几何操作目标也同样要有层次性。例如,第一学段“测量”中要求学生探索并掌握长方形、正方形的面积公式,会估计给定简单图形的面积。第二学段中“测量”要求学生探索并掌握平行四边形、三角形和梯形的面积公式,并能解决简单的实际问题。长方形的面积是通过猜想、实验、验证推导出来,平行四边形面积的推导则是通过剪、拼将之转化为长方形,再寻找两者之间的联系,从而推导出平行四边形面积的计算公式。可见,平行四边形的学习是建立在长方形知识经验的基础上进行迁移,目標的定位是逐渐提高的。再比如,在“图形与位置”中,一年级的学习目标定位在,结合生活情境会用“上、下、前、后、左、右”六个词来描述物体的相对位置。三年级的学习目标有所上升,要求学生能在给定“东、南、西、北”四个方向中的一个方向,能辨认其余三个方向;知道“东北、西北、东南、西南”四个方向,会用这些词描绘物体所在的方向。六年级的学生则要求能在具体的情况中,根据物体相对于观测点的方向和距离确定其位置,会描述简单的路线图。“图形的运动”中平移与旋转知识的操作目标也同样体现了层次性。二年级学习“平移与旋转”的目标,学生通过观察实例,初步感受生活中的平移与旋转现象,直观认识物体的平移与旋转;在观察、操作、演示活动中,让学生体会物体本身未发生变化,只是位置发生了改变,从而培养学生的空间观念。四年级学习“图形的平移”,学生观察、操作、实验进一步认识图形的平移,能准确地描述图形在方格纸上平移的方向与格数,能画出简单图形沿水平或垂直方向平移后的图形,充分积累几何操作经验。五年级学习“图形的旋转”,学生经历观察实例、操作想象、语言描述、绘制图形等数学活动,进一步认识图形旋转的特征与性质,能用三要素(旋转中心、方向、角度)描述图形旋转运动的过程,丰富了学生的几何操作经验。由此可见,后续的学习都是以前面的知识为基础的,教师在设定几何操作经验目标时要准确把握每个学段的不同要求,切忌拔得太高,本末倒置。
3.把握目标制定的主体性原则
教育家杜威在其《民主主义与教育》中提及,教育是一种生长,生长的具体过程和内在机制可以概括地表述为“经验的改组或改造”,这个过程不是一个通过灌输实现的被动过程,而是在个人积极主动参与共同生活的过程中能动地实现的。在数学学习活动中,教师要让学生经历观察、操作、猜测、验证、归纳推理、交流等活动,使学生获得的数学活动经验得到内化和提升。几何操作经验的积累更是如此,要让学生成为学习活动的主体,教师精心设计操作的材料、环节、关键之处进行点拔引导。教师不可替代学生操作、替代学生思考、交流、归纳与总结,离开了主体的参与,也就无经验积累可谈,几何操作经验目标的达成只能是一句空话。
例如,教学五年级下册“长方体和正方体体积的计算”一课,教师想为即将生日的妈妈亲手制作一个这样的蛋糕(长方体形状),想知道需要多少材料?其实就是要求蛋糕的体积,要知道蛋糕的体积,学生想出了两种办法,一种是把蛋糕切成1立方厘米的小正方体,看总共有多少个?另一种受以前学习的多种平面图形的面积计算的启发,想到了用公式计算的方法。长方体和正方体体积计算公式是怎样的呢?紧接着,学生展开了探讨长方体和正方体体积计算公式的学习活动。四人小组合作探究,分别利用不同数量的小正方体(棱长为1厘米)拼摆成各种长方体,并将数据填入表格中(见表)。
通过多组数据的汇总,观察、比较之后,不难发现长方体的长相当于每行的个数,宽相当于行数,高相当于层数。长方体的体积=小正方体的个数=每行的个数×行数×层数,长方体的体积=长×宽×高。整个过程,教师引导学生经历了探索长方体和正方体体积公式推导的全过程,学生在这样的操作、探索和交流思考的过程中,不仅获得了长方体和正方体体积的计算方法,还获得了如何去探索和发现知识规律的经验。本节课的几何操作经验目标:通过学生自主思考、合作探究、交流经历了长方体和正方体体积计算公式推导的过程,培养学生分析、比较、综合、归纳的能力,进一步发展学生的空间观念。目标的制定始终坚持以学生为主体的原则。
4.把握目标制定的可操作性原则
教师在几何操作活动经验目标的设定时要考虑到学生的实际水平,提出切实可行,具体明确的要求。切勿定过高或过低的目标,导致学生学习失去探究的兴趣,或操作活动变成走形式。教师在备课时,要充分考虑到操作过程中可能出现的情况,尽可能避免由于考虑失当导致操作失效的局面。合理预估不同水平的学生可能产生不同的想法、困惑,教师的引导也要提前设计好。
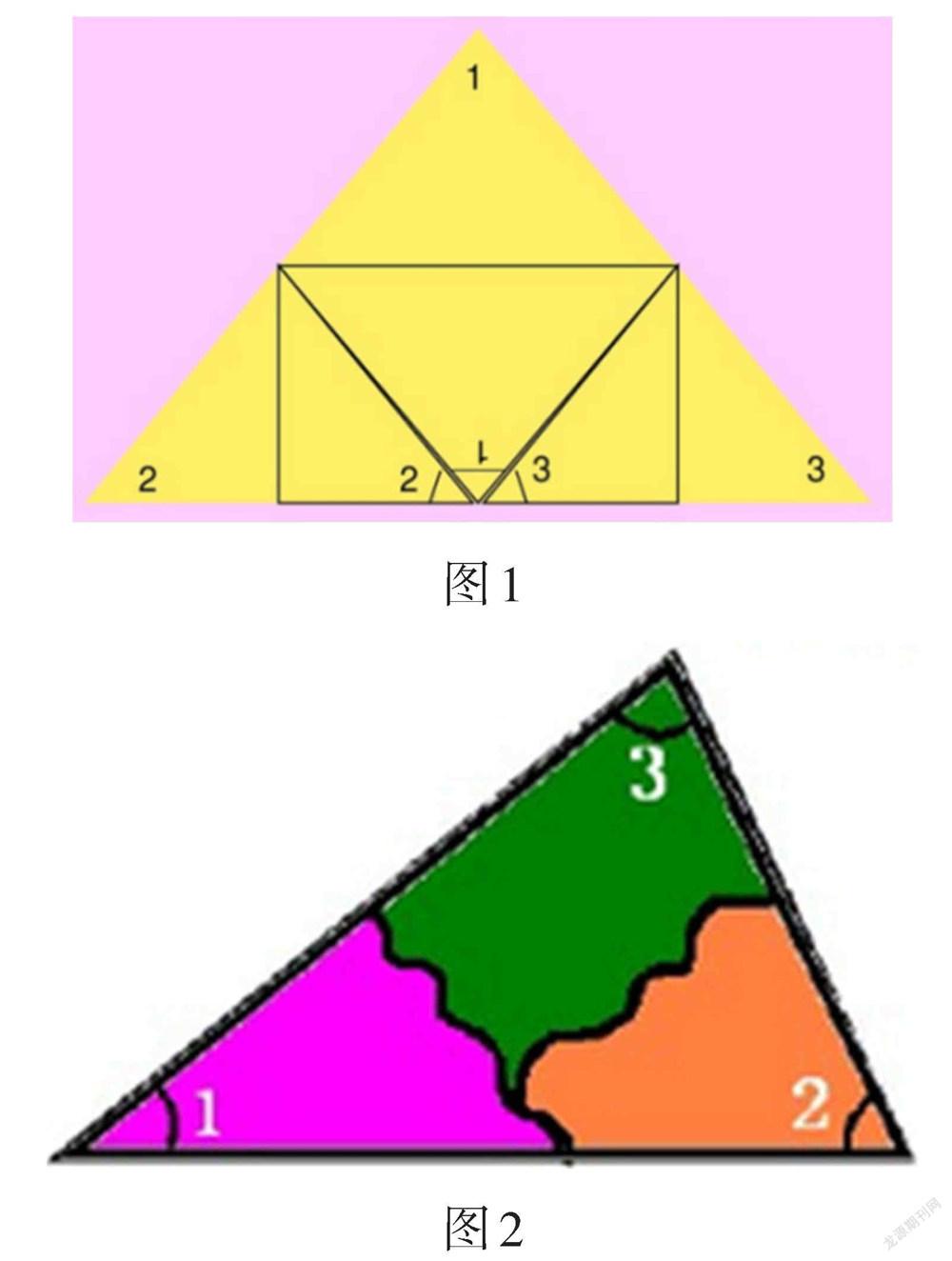
例如,教学人教版四年级下册“三角形的内角和”一课,几何操作目标定位:学生亲自动手,通过量一量、剪一剪、拼一拼等数学活动发现,得出三角形内角和是180度;并通过动手操作把三角形的三个内角和转化为平角的探究活动,向学生渗透“转化”的数学思想。部分学生在学习之前有所耳闻,已经知道三角形的内角和是180度。本节课教师要做的是要让学生用各种方式来证明已经知道的这个结论。通过教师的引导,学生通常会有以下三种不同的操作方式。第一种是让学生任意画出一个三角形(保证四人小组中至少有一个锐角三角形、一个钝角三角形和一个直角三角形),分别测量出三角形的每个内角的度数,再累加。由于测量会产生误差,导致内角和不是正好180度。所以很有必要再使用别的方法继续研究。第二种是学生用折的方法将三个内角向同一条边折下来(如图1),这样很容易就发现三个内角可以拼成一个平角,证实三角形的内角和是180度。第三种是将三个角剪下来,再将顶点靠在一起(见图2),也是把三个内角拼成一个平角,同样证实三角形的内角和是180度。
总之,积累几何操作经验需要学生主动探索,教师要引导学生展开为能达成三维目标行之有效的数学活动,要充分调动学生参与的积极性和主动性,突出学生的主体性,留给学生充裕的时间去探索和交流。因此,在制定几何操作经验目标时,要把握整体性、层次性、主体性、可操作性原则,流于形式的数学活动不仅无法让学生积累必要活动经验,学生的一些数学能力也随之弱化。
参考文献
[1]教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
[2]张奠宙,郑振初.“四基”数学模块教学的构建——兼谈数学思想方法的教学[J].数学教育学月报,2011(05).
[3]竺仕芬.促进学生数学基本活动经验积累的教学策略的思考[J].宁波教育学院学报,2014(03).
3943500589270

