基于数据特征的雷达径向干扰回波识别方法

卓健，廖胜石，周冬静，郭彬，苏彦，刘银焕

(1.广西壮族自治区气象信息中心，广西 南宁 530022；2.广西壮族自治区气候中心，广西 南宁 530022；3.崇左市气象局，广西 崇左 532200）

1 引 言

天气雷达产品广泛应用于短临业务中[1-4]，是短临预报的重要支撑手段。在实际业务中雷达会受到地物回波、电磁等诸多因素干扰，使用最大值拼图法制作雷达产品时，任何一部雷达受到干扰都会造成拼图产品存在干扰回波，使雷达产品图像受到破坏[5-8]。尽管预报员能利用丰富的经验避开干扰回波开展预报业务，但是在自动预报系统中，使用受干扰的雷达产品图像会破坏系统内各种气象要素正常的函数关系，导致发布错误的预报预警信息。

为提高雷达基数据和二次产品的质量，人们提出了不同的滤除干扰的方法。张富贵等[9]根据小波分解高频系数自适应确定阈值的方法，去除风廓线雷达地物杂波。刘黎平等[10]和江源等[11]对SA 雷达开展基于模糊逻辑的地物回波识别方法研究，李丰等[12]通过雷达观测数据对雷达地物回波特征进行分析，改进识别参量的隶属函数，建立适合地物识别方法，对C波段雷达地物回波特征进行识别。张林等[13]使用模糊逻辑算法在折射回波滤除算法基础上对强折射回波的滤除开展了研究。

径向干扰回波往往表现为条幅状干扰回波，它可能是由外部电磁干扰、内部数据处理或是天线对准太阳时引起。对于径向干扰回波的识别和滤除通常采用基于回波形态和基于功率法。如杜言霞等[14]根据干扰电磁波较为稳定，从较近的距离一直延续到雷达可探测到的最大距离处，存在于雷达回波图中连续几个方位上，其回波强度值几乎不变，径向干扰回波的区域，其边缘方位回波强度与相邻无干扰回波方位的回波强度差异较大的特点，使用同一距离库上相邻方位回波强度差，通过滤波法、插值法和功率法对径向干扰回波进行剔除研究。根据电磁干扰回波形态的识别和滤除算法已在ROSE等业务系统进行应用，文浩等[15]在“新一代天气雷达建设业务软件系统开发及应用（ROSE）”系统的业务试应用中，对雷达基数据质控方法进行定量评估，发现ROSE 系统所使用的质控算法能有效识别小于5 个径向的窄条幅状干扰回波。由于此算法已经限定了用于对比的径向回波宽度，只适用于小干扰角度的径向干扰回波识别和滤除，仍需改进算法完成对麻点状、螺旋状和大面积径向干扰回波的自动识别。文浩等[16]发现中国气象局气象探测中心现有的业务化径向干扰回波识别算法（AO）对大面积径向的干扰回波识别效果较差，针对径向干扰回波提出一种基于模糊逻辑方法的识别方法（AFL），AFL 只提取径向上的特征参量，对于径向干扰回波的识别准确率大幅度提高。

广西属于山地丘陵性盆地地貌，西北高、东南低，呈西北向东南倾斜状，目前全区有5部SB波段和5 部SA 波段共10 部新一代天气雷达。由于山岭绵密，以及电磁干扰等情况，广西新一代天气雷达在不同程度受到各种干扰影响，约超过10%时次的拼图产品会存在程度不等的径向干扰回波。当有干扰回波产生时，现有业务系统仅能滤除地物回波，以及少量的径向干扰回波，对于干扰方位角大、干扰强度强的径向干扰不能正确识别和滤除。对广西10部新一代天气雷达基本反射率因子产品进行拼图处理时，由于反射率因子产品本身不包含回波功率数据，所以前述方法不适用，需要另行开发一种新的识别算法。同时虽然单部雷达受干扰的比例不高，但拼图时使用多部雷达数据，受到干扰的概率和干扰的面积会大幅度提升，需要研究更好的通用干扰回波滤除算法。

本文使用广西10部新一代天气雷达的混合拼图产品，通过人工识别，筛选出受干扰的样本数据集。根据这组样本数据集的径向干扰特征，提出一种简明的径向干扰识别和滤除方法，期望能有效识别大方位角径向干扰并进行滤除，提高广西雷达拼图产品质量。

2 资料和处理方法

本文选用的雷达资料来源于广西业务运行的10 部新一代天气雷达，采用最大值拼图法将3 个低仰角（0.5 °，1.5 °，2.4 °）的基本反射率产品得到混合拼图产品，投影方式为等距圆柱投影（Equidistant cylindrical）。产品分为用于建模的训练数据集和检验模型泛化能力(generalization ability)的验证数据集。

2020 年1 月，广西多部雷达受影响程度不一的径向干扰，多时次的径向干扰幅度大、强度高，严重影响雷达资料的应用。通过人工识别出至少1 部雷达存在径向干扰的拼图产品作为训练数据样本，共166个样本。

验证数据集选自2019—2020年冰雹、台风、暴雨、飑线及晴天等天气过程的3 784 个样本（包括有或无干扰回波），各过程时间跨度为2～3 d。

3 识别和滤除方法

3.1 径向数据判定法

根据反射率因子Z（单位：dBZ）、回波功率与雷达最小可测功率之比B（单位：dB）的关系[17]，

式中，R（单位：km）为某观测点到雷达站的距离，A 是与雷达性能有关的常数（同一部雷达常数A相同），接收的B转换成Z时经过了20lgR 的距离订正，使得Z的大小随距离的增大有一定的增强。对多个样本的大幅度径向干扰样本观察发现，多数的大幅度、强度大的径向干扰，存在着整体上随着距离增长，干扰强度增强。

由于径向干扰回波一般是从雷达中心一直延伸到最远距离，呈条幅状的特点[18-19]，可以考虑从数据的形状特征进行识别和滤除。首先判别逐条径向数据为非干扰数据或可疑数据并做好标签，此为纵向判别，再将做好标签的可疑数据进行整体横向判别，当整片（≥1 条）的可疑数据被判定为径向干扰回波时，则在拼图时将这一整片数据整体删除，达到滤除干扰回波的效果。由于不预设判别宽度，所以能处理大方位角的径向干扰回波。我们将这一方法命名为径向数据判定法（Radial Data Determine, RDD），径向数据判定法是一种基于视觉的判定方法，核心在于如何实现客观判定。

3.1.1 径向干扰的数据特征

径向干扰由雷达信号处理器异常和信号受到外部电磁干扰引起。一般情况，所有仰角都可能出现径向干扰回波，在业务工作中，低仰角（0.5 °，1.5 °，2.4 °）的基本反射率产品更受人关注，需要着重分析这些仰角上径向干扰的数据特征。

图1 所示为柳州雷达2020 年1 月3 日两个不同时次受到径向干扰的2.4 ° PPI，图1a 在267 °、268 °方位角存在距离库长度不一致的两条径向干扰，其中268 °方位角从雷达中心一直到230 个距离库处都存在干扰，而267 °方位角的干扰仅延伸到145 距离库处，图1b 是同日另一时次的干扰，这次干扰的方位角幅度更大，从270 °方位角一直到318 °方位角都存在干扰，其中277 °方位角的干扰仅延伸到145距离库处。

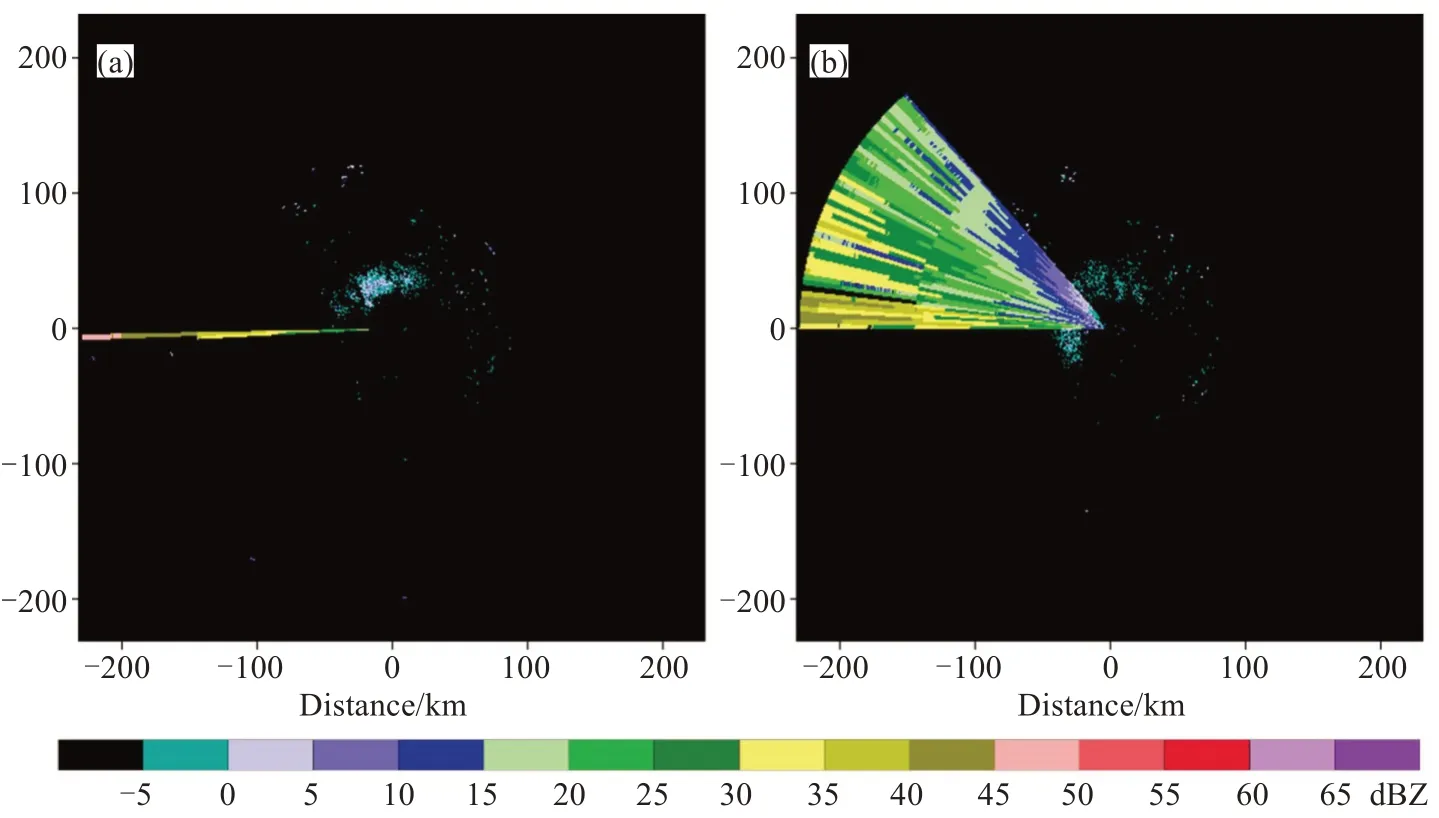
图1 柳州雷达2.4 °PPI a. 2020年1月3日00:36；b. 2020年1月3日03:00。

分析径向干扰的反射率因子产品可以发现，由于距离订正20lgR随距离变化较小，所以径向干扰回波在径向相邻库差异较小（图2），干扰随距离增加逐步增强，偶有较小的强度减弱，且大部分的径向干扰回波是由相邻方位角的干扰组成的一个干扰扇面。

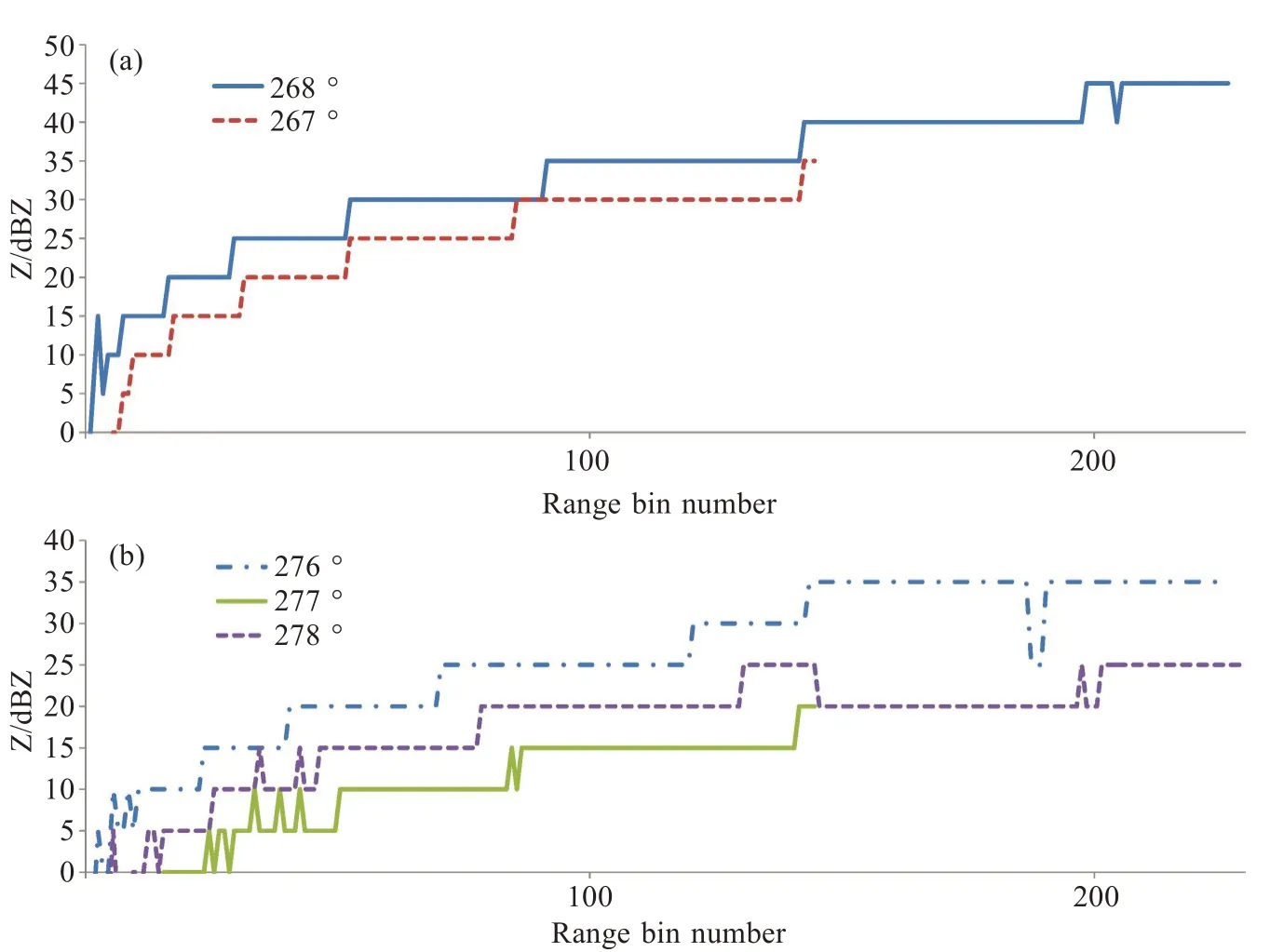
图2 柳州雷达径向Z随距离变化图 a. 2020年1月3日00:36，受干扰方位角；b. 2020年1月3日03:00，部分受干扰方位角。

3.1.2 特征参数

反射率因子产品径向干扰回波存在以下特征：

（1）单条的径向干扰数据，干扰延伸幅度大、结构紧密，反射率因子呈整体随距离增加而增强的特点；

（2）各雷达的不同仰角的径向干扰回波由多条组成连续的干扰扇面；

（3）径向干扰从较近的距离开始延续，径向干扰回波会连续多个方位角存在。

我们根据径向干扰的特征，提出四个新的特征参数用于对其进行描述精确描述。使用1 个方位-距离库为单位统计RDD 方法的特征参数，仅统计整条径向上至少有1 个距离库存在有效回波强度（干扰回波或非干扰回波）的径向数据条，从训练数据集中提取出了径向干扰回波10 948 条，非径向干扰回波124 592 条。四个新的特征参数CZ、CD、ME和SE的定义分别如式（2）～（7）：

式中，NR为反射率因子的距离库数，Zj（单位：dBZ）为方位角上某距离库的反射率因子，Val（单位：dBZ）为有效探测值，k为有效回波起始距离库。

（1）全径向回波计数CZ，表示每条径向基本反射率因子产品≥-5 dBZ 以上强度回波的计数。从数据形状形象的描述就是：有径向干扰的数据比无径向干扰的数据显得更“满”。识别出的干扰回波和非干扰回波的CZ概率分布见图3a，其中径向干扰回波长度为121～230 个距离库不等，其峰值为227 个距离库，共计1 025 条，占径向干扰回波总条数的9.362%，次峰值为142 个距离库，共计107 条，占径向干扰回波总数的0.977%。还发现CZ 达不到总探测距离库80%的径向干扰回波共1 371条，占径向干扰回波总数的12.523%，说明相对较短的径向干扰回波也占一定比例；而非干扰回波的有效回波占据的距离库较少。

（2）随距离增长逆向计数CD，表示从雷达中心向远端顺序计算本距离位置与下一距离位置之间，回波强度是否发生减弱现象，当差异值≤-5 dBZ时计1次。从数据形状形象的描述就是：有径向干扰的数据随距离增长越来越强。识别出的干扰回波和非干扰回波的CD概率分布见图3b，干扰回波的CD 则呈现较缓和的山峰状，其中CD∈[3,33]共10 288 条，占径向干扰回波全体比例的93.972%，非干扰回波的CD 呈尖锐峰状，计数为2的次数为峰值，共占总比例的21.2%。

（3）本径向回波强度最大值，用符号ME表示，代表本条径向数据回波强度的最大值。识别出的干扰回波和非干扰回波的ME 概率分布见图3c，表明径向干扰回波的最大值大于非干扰径向回波的概率更高。

（4）回波开始位置，用符号SE 表示，代表本条径向数据回波强度第一个≥-5 dBZ 出现的位置。识别出的干扰回波和非干扰回波的SE 概率分布见图3d，SE 表明干扰回波大多数从第4～6 个距离库处向远端延伸。

图3 干扰回波与非干扰回波的特征参数CZ(a)、CD(b)、ME(c)和SE(d)的概率分布

CZ和SE两个指标，将之前杜言霞等[14]提出的“干扰电磁波较为稳定，从较近的距离一直延续到雷达可探测到的最大距离处”，进行量化并形成指标，同时发现存在一定比例的干扰回波达不到探测距离的最大距离处，这类短长度径向干扰回波达不到文浩等[16]反射率因子在当前径向上的延展性达总径向的80%的要求。CD 指标则是针对反射率因子产品逐5 dBZ 分级划分回波等级的特点设计，与使用基数据识别和处理径向干扰回波存在较大差异。

3.2 建模及训练样本检验

决策树(Decision Tree）是一种可读性很强的分类方法，有非常成熟的算法。根据166个训练样本数据，得到可根据单条径向数据的特征从纵向判定径向数据是否为“疑似径向干扰回波”的决策树模型（图4）。

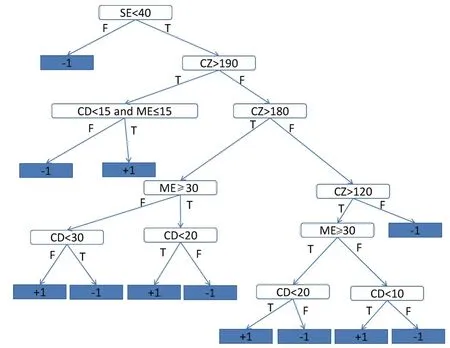
图4 纵向“疑似径向干扰”决策树

假如仅依赖单条径向数据进行判定，在台风、冰雹、飑线、暴雨等强对流天气过程时，某些正常的降水回波也会符合条件，可能会造成误滤除。针对径向干扰回波存在连续的方位角都受到影响，干扰回波呈“连片扇形”的特征，将这个扇面识别出来是解决大方位角径向干扰回波识别的关键，所以需要增加从横向判定径向数据是否“像”干扰回波。

（1）将多条连续的“疑似径向干扰回波”称为“疑似径向干扰回波块”。“疑似径向干扰回波块”定义为整块数据是有连续的“疑似径向干扰回波”，与该块回波相邻方位角的雷达数据是正常回波（图5）。本文查找“疑似径向干扰回波块”采用顺时针查找，先找到第一条“疑似径向干扰数据”将其命名为EI0，EI0逆时针方向前一条径向数据命名为EI-1，然后按顺时针方向依次找到下一条相邻的“疑似径向干扰回波”，直到最后一条“疑似径向干扰数据”命名为EIn，EIn顺时针方向的下一条数据为EIn+1，EI-1和EIn+1为正常回波，EI0顺时针至EIn为“疑似径向干扰数据”。

图5 “疑似径向干扰块”示意图

（2）使用“疑似径向干扰回波块”的EI0和EIn分别其相邻近的EIn和EIn+1进行比较，通过相邻两条数据差异度判定是否真的径向干扰回波块。相邻两条数据差异度使用ED表示，以EI0和EI-1为例则可如（8）表示：

由于实际业务中由于完全遮挡等原因存在，一个回波块的完全遮挡区边缘会被误判为EI-1或EIn+1，所以根据“疑似径向干扰块”组成的“疑似径向干扰数据”条数不同采用不同的判定标准（图6）：当“疑似径向干扰块”仅由一条“疑似径向干扰数据”条组成时，使用双侧判定，即这条“疑似径向干扰数据”与其顺时针及逆时针方向的相邻数据存在较大差异时判定这个“疑似径向干扰块”是真实的径向干扰回波，当“疑似径向干扰块”由一条以上的条组成时，使用单侧判定法，即EI0与EI-1或者EIn与EIn+1存在较大差异时，判定这个“疑似径向干扰块”是真实的径向干扰回波，EI0与EI-1判的差异用ED0,1表示，EIn与EIn+1的差异用EDn,n+1表示。对于单条“疑似径向干扰数据”ED0,1且EDn,n+1均＞0.3 则判定该条“疑似径向干扰数据”为径向干扰回波块；对于多条“疑似径向干扰数据”组成的“疑似径向干扰块”，若ED0,1且EDn,n+1均＞0.3 或ED0,1＞0.85 或EDn,n+1＞0.85 则判定该条“疑似径向干扰块”为径向干扰回波块。这里的判定的ED 阈值为经验值。“疑似径向干扰块”若判断为“真”，那么整块径向干扰数据进行滤除，加入“疑似径向干扰块”与其相邻的正常回波进行比对后，大幅度降低误识别的风险。

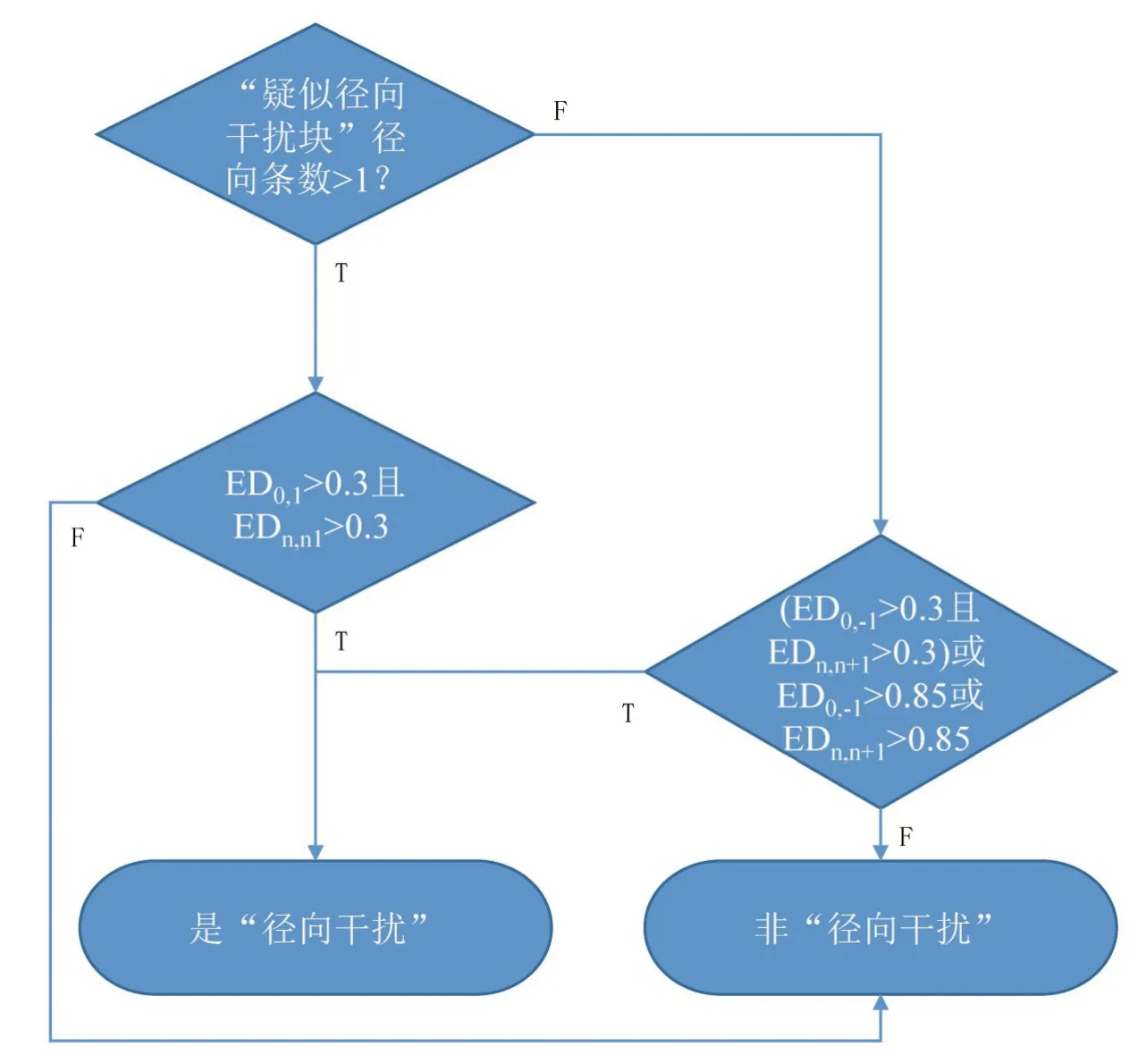
图6 “疑似径向干扰块”判定流程图

3.3 检验评估标准

使用径向数据判定法对雷达数据的径向干扰回波进行识别和滤除，得到质控后的拼图产品，将其与不进行质控最大值拼图法产品进行比对，检验径向数据判定法对径向干扰回波的识别性能，由人工进行定性评估，辅助定量评估。

3.3.1 定性评估

定性检验评估由人工进行判定。为检验训练数据集的识别效果，对单站干扰回波由幅度和强度进行定义，根据径向干扰方位角的多寡，分为两类：

小幅度干扰：该时次电磁干扰回波总数＜30条扫描数据；

大幅度度干扰：该时次电磁干扰回波总数≥30条扫描数据。

根据径向干扰强度，分为三挡：

高强度干扰：该时次电磁干扰回波强度最大值≥30 dBZ；

中强度干扰：该时次电磁干扰回波强度15 dBZ＜最大值＜30 dBZ；

低强度干扰：该时次电磁干扰回波强度最大值≤15 dBZ。

识别和滤除效果一共分为五档：完美：所有径向干扰得到滤除；良好：滤除中、高强度干扰，剩余部分低强度干扰；

一般：滤除较多的主要的径向干扰，剩余部分存在一定量的中、高强度干扰；

较差：存在较多的中、高强度干扰；

失败：滤除识别失败，未进行滤除；

误滤除：当滤除算法将正常回波删除时定义为误滤除。

3.3.2 定量评估

定量评估主要检验使用RDD 方法后的拼图与使用最大拼图法后的拼图之间的差异，用整体差异度TD进行评估：

式(9)中各变量定义如下：以拼图区域（103～113 °E，19～27 °N，分辨率0.01 °）逐像素比对，若两像素不同则差异总数（dif）加1，两像素相同则无差异总数（sam）加1，TD 仅统计反射率因子≥-5 dBZ 的有效区域。TD 取值范围为[0，1]，数值越小说明两图差异越小，若为0 则说明两图片没有差异，为1则说明两图片没有任何相似之处。定量评估仅用于验证数据集检验，方便判定是否采用径向判定数据法对存在差异的样本进行深入分析。

4 训练样本检验

根据3.3.1 节的定性评估定义，人工判定使用径向数据判定法滤除径向干扰回波后与不使用任何滤除技术的最大值拼图法拼图[7]比较，训练数据集的识别效果见表1。训练数据集没有发生误识别和滤除现象，这是由于训练数据集样本的径向干扰没有混杂在降水回波中，且由于是使用全集进行建模所以识别效果显得非常良好。

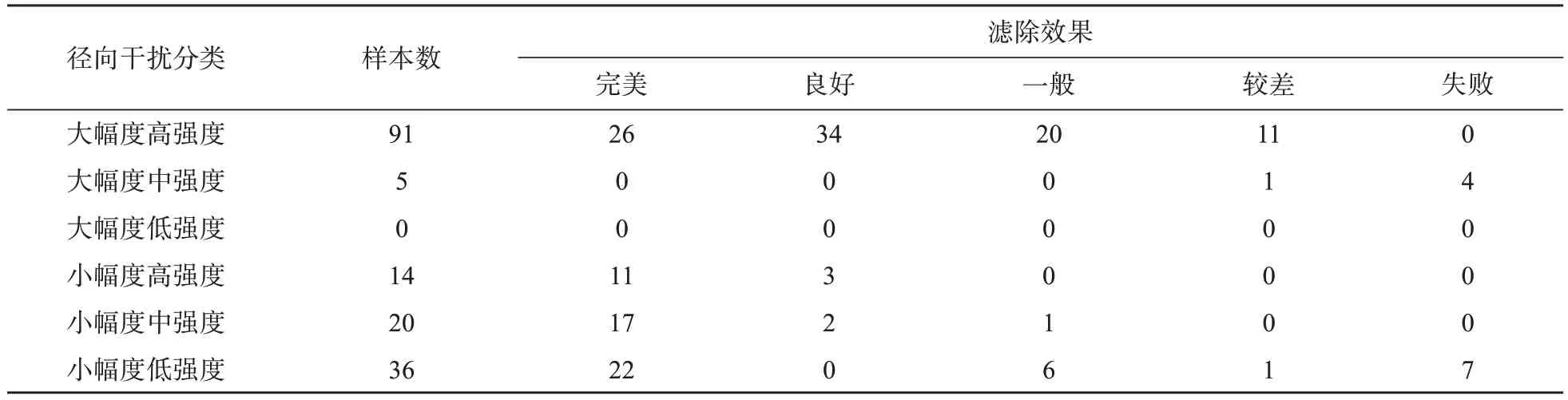
表1 训练数据集径向干扰回波识别滤除情况表

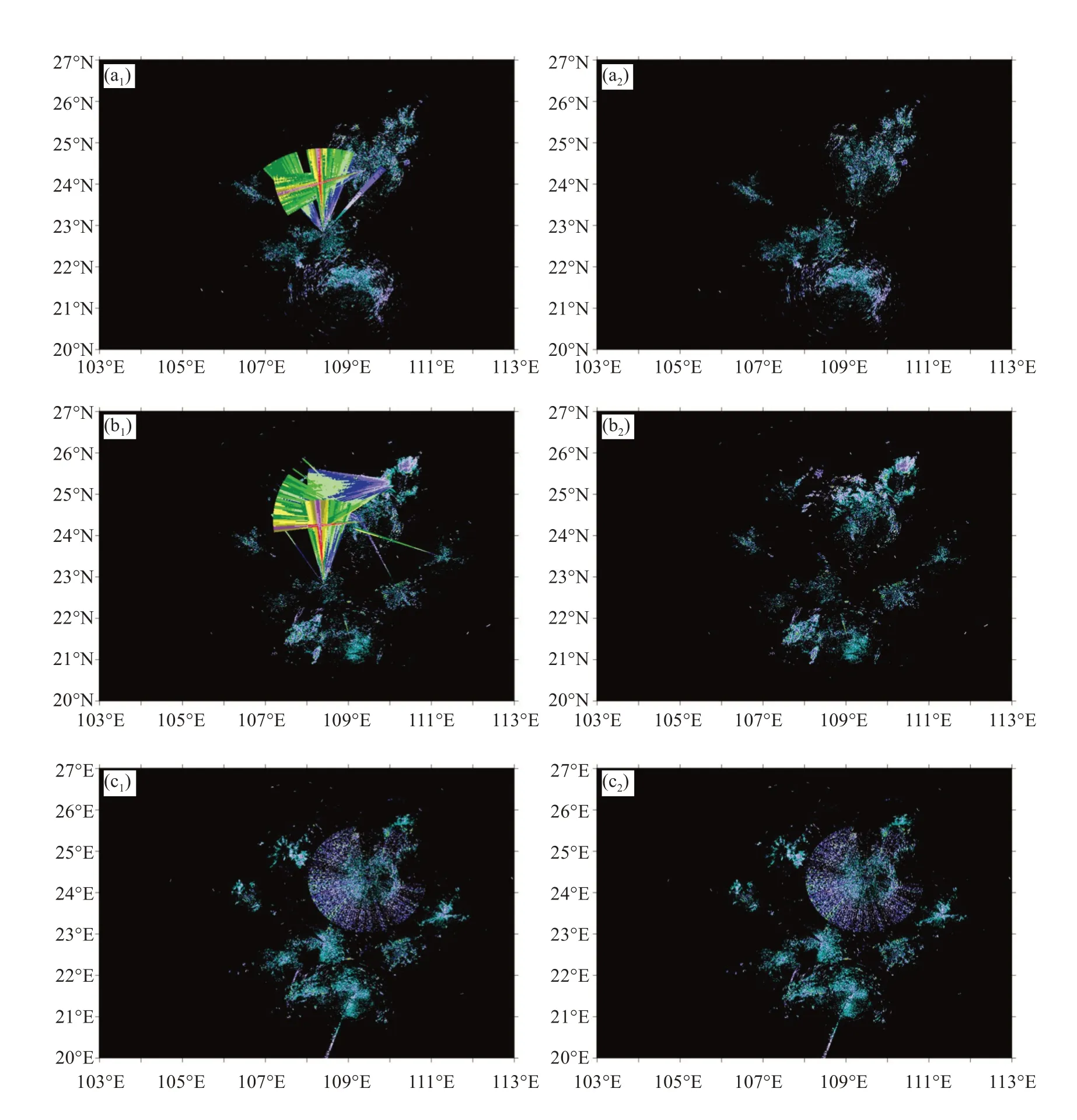
大幅度高强度样本数总共91 份，占总样本数的54.8%。其中共26 次（占此类样本数28.6%，下同）完美滤除，34 次（37.4%）良好滤除，20 次一般滤除（21.9%），11次（12.1%）较差滤除，0次失败滤除。完美滤除例子如2020 年1 月7 日13:12（图7a1），滤除了影响南宁、柳州雷达的径向干扰回波，得到没有干扰的拼图（图7a2）；良好滤除例子如2020 年1 月3 日03:18（图7b1），滤除了南宁、桂林、柳州、梧州、玉林雷达的径向干扰回波，仅北海雷达西北侧有多条短径向干扰回波未能滤除（图8b2）。

大幅度中强度共1 次（20%）较差滤除，4 次（80%）失败滤除。2020 年1 月4 日05:00（图7c1，7c2）是一次失败滤除例子，属于罕见的干扰类型，各径向干扰多次不连续，RDD算法未能正确识别。

小幅度高强度共11 次（78.6%）完美滤除，3 次（11.4%）良好滤除。这类干扰回波由于幅度小，强度强，RDD 均能较好识别和滤除，如2020 年1 月4日12:54（图7d1、7d2），通过滤除柳州雷达的径向干扰回波，得到没有干扰的拼图。

小幅度中强度共17 次（85%）完美滤除，2 次（10%）良好滤除，1 次（5%）一般滤除。这类干扰回波滤除情况类似小幅度高强度干扰。

小幅度低强度共22 次（61.1%）完美滤除，6 次（16.7%）一般滤除，1 次（27.6%）较差滤除（2.8%），7 次（19.4%）失败滤除。这类干扰由于幅度小，强度弱，RDD 方法识别率较低。如图7e1、7e2所示，2020 年1 月12 日23:42，桂林、柳州雷达东南侧各存在一条较弱的干扰回波带，由于干扰回波太弱，不符合径向数据判断法中ME的定义，故未能识别和滤除。

图7 2020年1月7日13:12（a1、a2）、1月3日03:18（b1、b2）、1月4日05:00（c1、c2）、1月4日12:54（d1、d2）、1月12日23:42（e1、e2）训练样本检验示例

5 应用验证分析

由于用于建模的样本都没有大面积降水回波，为了检验RDD 方法的泛化能力，特别是干扰回波混杂在降水回波内时的识别和滤除能力，我们从2019—2020 年不同天气过程筛选了共3 784时次的样本进行应用检验，这些天气过程包括冰雹、台风、暴雨、飑线等强对流天气过程和1次冬季晴朗天气过程，各过程时间跨度为2～3 d，序号2、3有部分时次雷达数据缺失。表2 给出验证数据集径向干扰回波识别滤除检验结果，其中“不能确认”为RDD 方法客观判断为存在径向干扰并滤除，但经过人工识别，发现干扰回波面积极小，滤除前后的拼图几乎无差别的样本。表2 中CSI 为临界成功指数，定义如式（10），

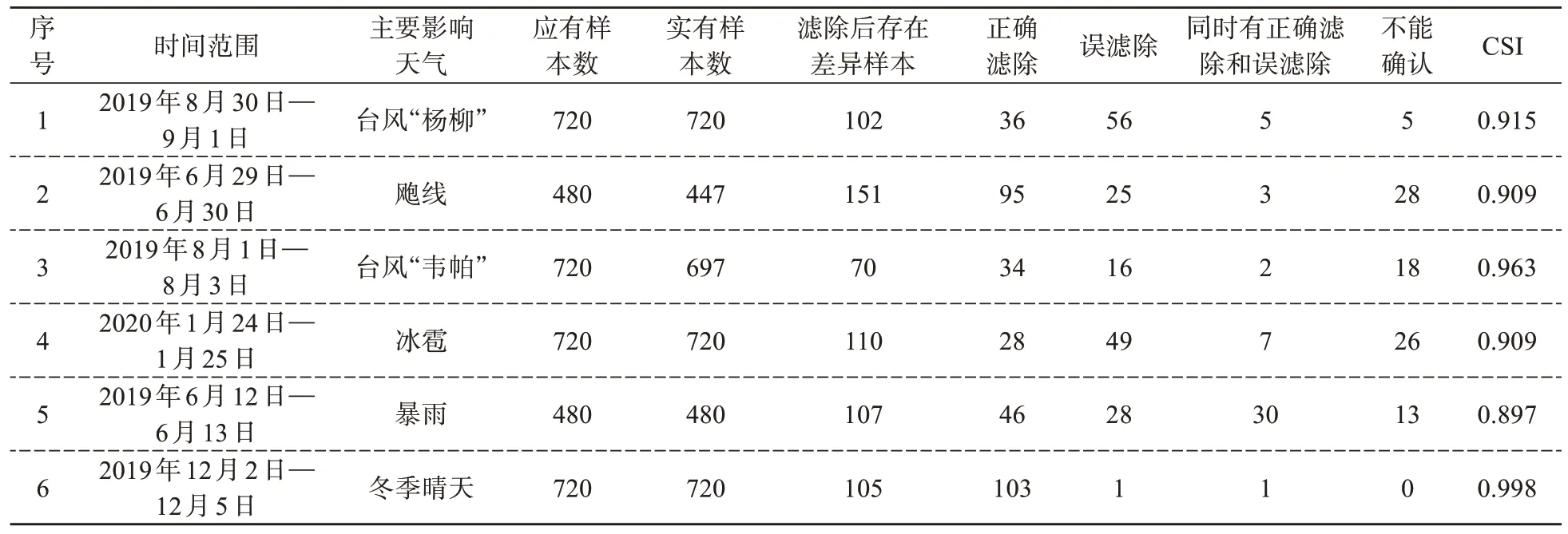
表2 验证数据集径向干扰回波识别滤除情况表

式中NALL为所有参与评估的样本数，NA 为正确识别的样本数，对于“同时有正确滤除和误滤除”和“不能确认”计0.5次NA。

我们选择一些有特点的样本对验证效果进行说明。

例1：2019 年8 月30 日17:30，本次拼图（图8a1，8a2）崇左雷达因干扰产生严重的径向干扰现象，多条径向干扰数据无规律分布在各方位角。该时次崇左雷达南部为台风“杨柳”外围云带，雷达站其他几个方位存在面积不同的破碎回波块，干扰回波和正常回波混杂在一起，若不进行干扰回波的识别和滤除，那么在客观系统中会严重破坏QPE/QPF。RDD 方法对于混杂在降水回波中的径向干扰回波进行有效识别和滤除干扰回波，仅崇左雷达西北侧残余一条窄且弱的径向干扰回波未被滤除，原因是这条干扰径向回波是强径向干扰回波的很弱的次生回波，不符合RDD方法。

例2：2019年6月29日11:24，柳州雷达西侧为一块带状回波，有一条向西北侧延伸的径向干扰回波贯穿其中（图8b1白色箭头指示），这条干扰回波被正确识别出来，滤除后的拼图没有对正常回波造成破坏（图8b2）。

例3：2019 年8 月1 日04:12，从南宁雷达向东北侧延伸的径向干扰回波贯穿大面积降水回波（图8c1白色箭头指示），这条干扰回波也被正确识别出来并进行删除，但是本例中在拼图东侧有极小一部分正常的回波被误滤除（红色方框区域内），这是由于梧州雷达东侧是一个大方位角的完全遮挡区，这个遮挡的存在对径向数据判定法造成了破坏。

例4：2020年1月25日10:24，防城港雷达和南宁雷达西侧各有一组径向干扰回波且混杂在降水回波中（图8d1白色箭头所指位置），被正确识别出来和滤除，滤除后的拼图未影响正常降水回波。值得注意的是，这一样本并没有在166个训练样本中出现，说明这一时次大面积降水回波中蕴含的两条微弱干扰回波不太明显，人工主观没有标注出来，但是客观模型能精确找出。

例5：2019 年8 月1 日05:00，人工判定本次拼图不存在径向干扰回波，但是RDD 误将南宁雷达西侧一个方位角的回波误滤除（图8e1白色箭头所指位置），同时被误滤除的还有梧州雷达东侧的极小一部分降水回波误滤除了（图8e1红色方框区域内），原因同例3，这是3 784个样本中误识别、误滤除比例最高的一个样本，TD=2.25%，仅为有效回波区域的一小部分，梧州雷达东侧被误滤除的回波因为有其他仰角的反射率因子进入拼图产品，该区域的影响效果是回波偏弱，不影响拼图整体效果，是一种可接受的损失。

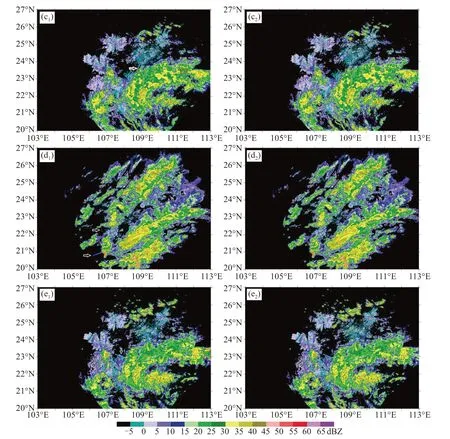
图8 2019年8月30日17:30（a1、a2），2019年6月29日11:24（b1、b2）、2019年8月01日04:12（c1、c2）、2020年1月25日10:24（d1、d2）、2019年8月1日05:00（e1、e2）验证数据集检验示例

对表2做进一步分析：

（1）RDD方法能较好地识别径向干扰回波，识别准确率高，在6 种天气过程中，平均CSI 为0.932。正确滤除和同时存在正确滤除样本共390次，占总样本10.3%，说明选择的样本时段，拼图受干扰的概率较高。任一部雷达受干扰是一个概率事件，当多部雷达进行组网拼图时，任一时次拼图受干扰的概率则由组网雷达受干扰的联合概率影响。这也说明开展径向干扰识别和滤除非常有必要；

（2）误滤除的样本共175 次，占总样本4.62%，这些样本按时序排列见图9，共12 次样本误滤除面积超过当时次回波面积的1%。最大一次占当时回波面积的2.25%（图8e），相当于拼图区域的0.55%。由于广西自然地形、建筑的雷达完全遮挡区是造成本类误滤除的主要原因；

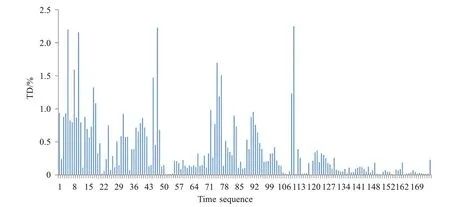
图9 误滤除回波与拼图回波比例

（3）人工无法通过肉眼区分存在差异的拼图样本是否存在径向干扰共90 次，占总样本2.38%，这些差异占回波面积非常小，有无干扰都不影响使用。

以上分析表明RDD 方法能较好地识别和滤除径向干扰回波，识别率高。训练数据集没有包含降水回波，验证数据集由于主要从强对流天气中选择，包含很大比例的降水回波。训练数据集和验证数据集属于相关性较差的不同数据集，并且验证数据集数量远远超过训练数据集，这说明RDD 方法具有良好的泛化能力，能有效在业务系统中进行应用。

6 结论和讨论

径向干扰回波存在一定的特征，有些特征如“从较近的距离开始”、“连片”等未进一步在识别和滤除研究中进行应用，本文根据径向干扰回波的数据形状特征将其量化，设计一种对径向干扰回波进行简明高效的识别和滤除的方法：RDD法。RDD 法提出全径向回波计数、随距离增长逆向计数、本径向回波强度最大值和回波开始位置等4个新的统计参数，先通过决策树模型确定疑似径向干扰回波，再将疑似径向干扰回波连片进行整体识别，效果评估结果如下。

（1）RDD 方法通过纵向和横向对反射率因子数据形状进行识别，不预设识别方位角阈值，能够有效识别出大幅度的径向干扰回波，且发现广西新一代天气雷达存在一定比例之前学者未提及的较短长度的径向干扰回波。

（2）RDD 方法对径向干扰没有混杂在大面积降水回波中的166个训练样本，没有发生误识别和滤除现象，其中大幅度高强度样本28.6%完美滤除，37.4%良好滤除，21.9%一般滤除，12.1%较差滤除，0次失败滤除。训练数据集的识别效果很好。

（3）RDD 方法对5 次径向干扰混杂在降水回波中的降水过程、1 次非降水过程共3 784 个检验样本，能正确滤除径向干扰样本390 次，占总样本10.3%，误滤除样本175 次，占总样本4.62%，绝大多数误识别造成的正常回波损失小于当时次回波面积的1%，仅有12个样本超过当时次回波面积的1%。RDD 方法的正确识别率高，误识别率损失小。

（4）RDD 方法具有良好的泛化能力，具有良好的业务应用前景。

（5）RDD 方法误识别主要是由于广西地形造成的遮挡引起。

本文讨论的径向数据判定法仅从单仰角产品进行判定，由于雷达逐仰角扫描产品在空间上是连续的，可以考虑将相邻仰角的产品一起考虑，这样在纵、横两个方向的基础上增加了上、下方向数据判定，数据使用维度提升到3D，可以进一步增强识别准确率。同时正确的识别出雷达的自然环境和建筑物遮挡区是进一步研究的基础，遮挡区识别算法已经有很好的研究可以借鉴[20-21]。具体模型的建立是我们下一步研究的方向。