某型船主配电网路使用初期可靠性评估*

杜春雨 姜海龙 王宗亮

（海军潜艇学院 青岛 266000）

1 引言

主配电网路是某船电力系统的主干，持续维系着船舶的生命与安全性。主配电网路是某型船配电网路系统的主体部分，按电制可分为交流主配电网路和直流主配电网路两部分［1］。交流主配电网路又可分为正常网路与可靠网路两部分。主配电网路通常采用馈线式结构、分舷配置、分区供电的方式不间断地满足全艇人员和装备的用电需求［2～3］。

网路故障是影响电力系统安全稳定运行的重要因素［4～7］。以系统可靠性模型为基础，通过多种经典数学模型对系统故障与运行时间的相关性进行系统分析，预测总结故障规律，可为提升电力系统安全性和可控性提供帮助。

2 某船主配电网路可靠性分析

建立主配电网路模型（如图1），AD为直流配电板，AR为可靠配电柜，FD21、FD22为柴油发电机，ZD11、ZD12为变流装置及其附属设备，JLD为岸电装置，YDJ为应急发电机，YJ为应急发电机开关板，K1、K2、K3、K4、K5、K6、K7、K8、K9为主网路中的主干支路开关。

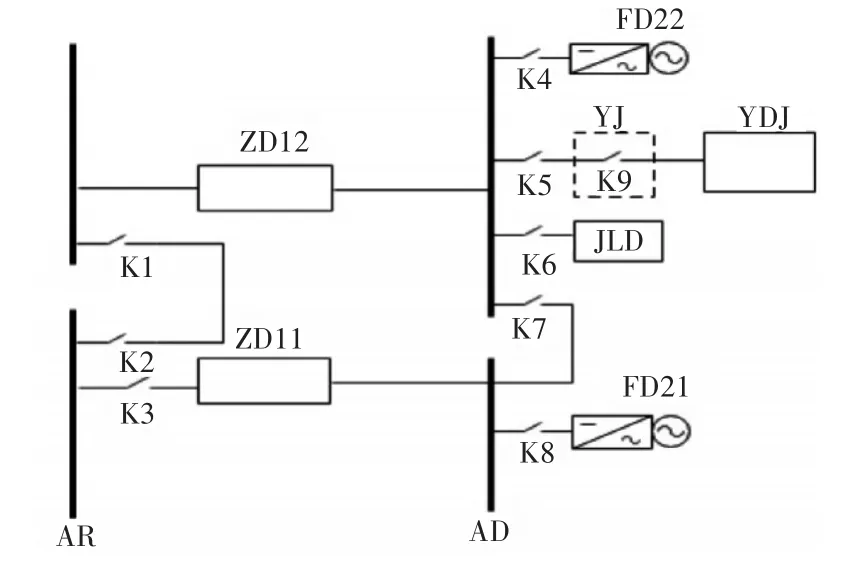
图1 主配电网路模型

主配电网路实现的是将交流电能和直流电能，根据不同的要求，通过AR、AD以及分布于各舱室的配电板、配电箱分配给负载使用［8］。

为实现对某船主配电网路的可靠性分析，收集了某型船两年来（共计1213例）网路故障数据，经整理分析，初步得出该船主配电网路中各设备的故障发生概率如表1所示。

由表1可以看出，主配电网路设备故障率不尽相同，但都存在着一定的故障隐患，对某船电力系统生命力将产生直接影响。

表1 某船主配电网路设备故障率

从某型船故障数据分布情况看，该船主网路设备故障分布具有一定的时间相关性，这使得探索设备的预期寿命成为可能。

3 基于数据处理的寿命评估模型

根据前述收集的主配电网路设备故障发生的时间，并绘制成表，探寻网路出现故障的时间与经典数学函数间的关系。这里将各分布函数线性化（y=Bx+A）利用线性回归分析法将实验数据拟合，以显著性差异为前提，选取相关系数r绝对值最大的为母本函数计算其最佳估计值，则估计值为最佳线性无偏估计［9］，将统计数据由小至大排列如表2。

表2 某船主配电网路设备故障时间统计

表2中i为次序号（i=1，2，3，…，n），n为测试数据的总数，截尾子样为t1≤ t2≤ … ≤ tk，k≤ n），设F（ti）为连续随机变量函数f（t）概率密度函数，对于F（ti）的估计有许多经典方法，例如：中位秩数值；等，文献［10］中表示F(ti)=中位秩数值对于子样作定数截尾试验较好，这里使用中位秩数值：

作为估计值（根据式（1）计算后，如表3）。

表3 主配电网路故障时间对应概率表

通过对经典函数线性化求得相关参数值。根据数据点（ti，F（ti））可求得（xi，yi），利用（xi，yi）作回归分析求得y=Bx+A中估计值A^、B^和相关系数r的值。

3.1 指数函数分布

根据指数函数分布：

线性化得：

其中δ为位置参数，θ为平均寿命。

3.2 威布尔分布

根据三参数威布尔分布函数：

当δ=0或作变换令x=t-δ即可得到二参数威布尔函数：

线性化得：

其中m为形状参数，η为尺度参数，t为位置参数。

3.3 对数正态分布

根据对数正态分布函数：

线性化得：

其中σ为尺度参数，μ为位置参数。

3.4 幂函数分布

根据幂函数：

线性化得：

3.5 Z函数分布

根据Z函数［11］：

线性化得：

相关参数值如表4。

表4 算后参数值

经表4中相关系数r数值对比可知，对数正态分布的相关系数r最大，所以正态分布函数可以近似表示寿命分布Ti。

4 模型实例运算与分析

根据式（7）对数正态分布函数构建数学模型（如图2）。

图2中，点“o”为（t，F（ti））点，实心线为符合对数正态分布函数的拟合值。

图2 对数正太分布图

根据文献［12］中公式推导解得：

对数正态分布密度函数为

可靠性寿命：

其中：

置信区间：

分布密度函数如图3所示，置信区间得以验证。

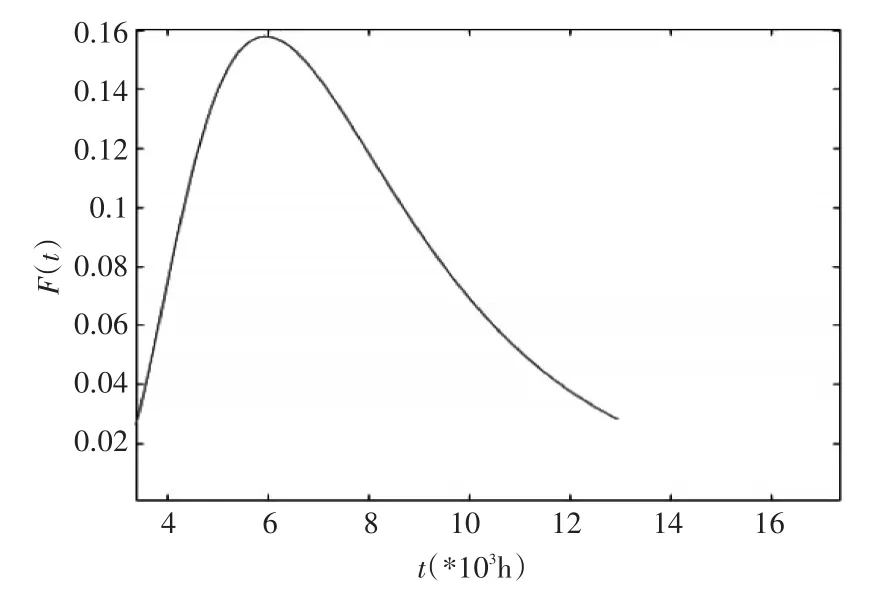
图3 分布密度函数图

由图2验证可得，主配电网路的无故障时长分布基本符合对数正态分布，在4.4992千时至6.9120千时区间出现网路故障率显著增加的现象，后趋于平稳，系统故障发生呈现时间相关性。

针对系统这种典型的时间相关故障概率分布，提出针对性的改进系统可靠性的建议：

一是优化电力系统PHM。将主配电网路的运行时间作为系统监测的重要参数，当网路系统累计运行时长达到4.4992至6.9120千时区间内，应对直流配电板相关组件、应急发电机开关板以及其他开关板、断路器等重点设备进行重点监测维护。通过时间参数监测，及时评估电力系统可靠度，支持装备精准维护、精确维修。

二是优化系统设计。网路设备增加人机接口，增加大数据采集分析以增强状态监测能力。提升操作人员对装备状态掌握的实时性、快捷性。同时收集的数据也可提供给装备研制单位，为进一步完善同型网路提供数据支持。

5 结语

上述针对某型船主配电网路故障的研究，探索了网路系统使用初期故障概率的时间相关性。究其原因，主要是网路设备还是以相对简单的传统型设备为主，这类设备使用初期为初始故障期，其故障率明显偏高，故障的时间相关性显著。

当然，本项研究选取的研究阶段为装备使用初期，收集的数据并不能涵盖装备全寿命阶段，数学模型存在一定的局限性。随着后续对该型装备系统的持续跟踪，可以梳理出更加可靠的装备全寿命期故障规律。