面向帕金森病语音诊断的非监督两步式卷积稀疏迁移学习算法

张小恒，张馨月，李勇明，王 品，刘玉川

（1.重庆大学微电子与通信工程学院，重庆 400030；2.重庆广播电视大学，重庆 400052）

1 引言

帕金森病（Parkinson’s Disease，PD）是全球第二大退行性神经疾病，危害严重［1］.语音障碍作为PD 的显著症状又叫作PD 构音障碍［2］.基于语音数据的PD 诊断方法具有简易、高效、非接触等特点，因此深入研究PD 语音诊断具有重要的科学意义及实用价值.近年来已有大量PD 语音诊断算法出现，但其预测精度仍有较大提升空间.

常用的PD 语音特征分为基音相关类、能量相关类、语速相关类及内容相关类［3，4］.特征选择/变换方法主要可分为基于神经网络方法［5～7］、基于主成分分析方法［8］、基于串行搜索方法［3，8］、基于进化计算方法［7］，还有P 值［4］、线性判别分析（Linear Discriminant Analysis，LDA）［9］等方法.常用分类器主要有支持向量机（Support Vector Machines，SVM）［3～5］和K 近 邻（K-Nearest-Neighbor，KNN）［3，4，10］，还有随机森林（Random Forest，RF）［3］、贝叶斯网络［11］、概率神经网络［12，13］和决策树［13］等.

值得注意的是，上述算法均仅基于本地PD 语音数据集.如前所述，本地PD 语音数据集存在小样本问题，限制了准确性的提高.研究表明，迁移学习方法可以有效解决这类难题［5］.相关研究［3，5］已证实了迁移学习在PD 诊断中的有效性，但这些诊断方法都不是基于语音数据的.此外，这些文献中的迁移学习方法都只涉及从源域到目标域的一步迁移，且未考虑本地PD 语音集中训练集和测试集的不同受试者数据之间的分布差异.虽然已有学者将训练集和测试集看作不同域进行了迁移学习研究［14］，但都未涉及PD语音分类领域.总之，现有的PD 语音诊断算法研究，既未考虑利用迁移学习来解决小样本问题，也没有考虑通过域适应方法减少训练集与测试集的数据分布差异.上述问题亟待解决.

近年来，图像处理研究领域出现一种新颖的稀疏学习算法——卷积稀疏编码（Convolutional Sparse Coding，CSC）算法.该算法具有很强的稀疏学习能力，能够有效地获取数据中隐含的结构与模式［15］，适合于提取PD语音数据中的隐藏信息.此外，基于relief算法［16］，本文构造了语音段特征同时优选算法，挖掘了更有效的信息，拟与CSC 结合，设计第一步迁移学习算法（First Step Transfer Learning Algorithm，FT）.域适应的目的是在不同但相关的任务或领域之间转移共享知识［17］.非监督域适应（Unsupervised Domain Adaptation，UDA）的常见做法是尽量减少域之间的差异，以保持域不变特征［18］或在执行域对齐时学习更多有差异的特征.因此，本文考虑将其用于PD 语音数据域适应，保持训练集（源域）和测试集（目标域）各自局部结构特性不变的同时，减小领域之间的分布差异.基于此，本文提出了一种新的域适应方法——联合局部结构信息分布对齐（Joint Local Structure Distribution Alignment，JLSDA）算法，从而在分类之前降低了训练集与测试集之间的分布差异，有助于提高分类准确率.结合上述两步迁移学习算法，本文提出了一种新的PD 语音诊断方法——非监督两步式卷积稀疏迁移学习（Unsupervised Two-Step Convolutional Sparse Transfer Leaning，TSTL）算法.

本文的主要贡献和创新点如下.

（1）为了解决PD 语音诊断中小样本和训练集测试集间分布差异这两大问题，本文提出了非监督两步式卷积稀疏迁移学习算法（TSTL）.该算法同时将不同数据集之间的迁移学习与同一数据集中训练集与测试集之间的迁移学习相结合.

（2）为了提高迁移源数据集效率，将CSC 算法与语音段特征同时优选算法相结合，基于傅里叶域并交换迭代次序的交替方向乘子法提出了第一步迁移学习算法——语音段特征同时优选的快速卷积稀疏编码（Fast Convolutional Sparse Coding with Coordinate Selection of Samples and Seatures，FCSC&SF）算法.

（3）本文针对PD 语音集中训练集和测试集的分布差异问题，首次提出了联合局部结构信息分布对齐（JLSDA）算法.

（4）本文将受试者多个语音段样本合并转化为二维数据样本，用于迁移学习算法的建模和验证，并充分考虑了语音段和特征之间的协同关系.

2 方法

2.1 相关符号描述

2.2 算法研究

本文提出的面向帕金森语音诊断的非监督两步式卷积稀疏迁移学习（TSTL）算法主要包括两部分：第一步迁移学习算法为语音段特征同时优选的快速卷积稀疏编码（FCSC&SF）算法，第二步迁移学习算法为联合局部结构信息分布对齐（JLSDA）算法.第一步迁移学习算法的目的是学习公共语音集（源域）中的有用信息并将其迁移到目标域.第二步迁移（JLSDA）的目的是对齐数据分布同时保持原始结构不变，降低训练集和测试集之间的分布差异.

2.3 第一步迁移学习算法(FT)——语音段特征同时优选的快速卷积稀疏编码(FCSC&SF)算法

2.3.1 快速卷积稀疏编码

其中，xg=是G0×N分块矩阵，eg,k是G0×N特征映射矩阵，与对应的卷积核dk进行卷积运算逼近xg，符号*表示二维卷积运算，η是大于0的正则化因子.式（1）可进一步简洁表达如下：

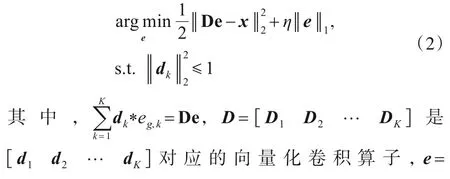
上述优化问题可基于经典的交替方向乘子法（Alternating Direction Multiplier Method，ADMM）实现［19］.由于源数据集规模较大，训练时间较长不利于实际应用，为实现高效运算，本文基于文献［20］的傅里叶域快速运算并结合文献［21］的交换迭代次序法加以解决.其特征映射部分训练部分如下：

其中，Fsupp(d)是一个蒙板函数，支撑集SUPP(d)上为1否则为0，γ是松弛因子.

式（3）、式（4）中step1 的时间复杂度等同于文献［20］，但由于step2的时间复杂度极低，因此本文提出的快速卷积稀疏编码（FCSC）算法整体迭代效率远高于文献［20］.

目标域F的特征映射变换如下：替换x，用训练好的卷积核替换D，基于式（3）通过有限次迭代可将目标域特征矩阵可转换为特征映射矩阵e=可以选择固定的ek作为映射，从而构建转换后的目标域特征矩阵

2.3.2 语音段特征同时优选

FCSC&SF算法伪代码描述如算法1所示.

2.4 第二步迁移学习算法——联合局部结构信息分布对齐(JLSDA)算法

本文提出一种新的通过映射源域（训练集）和目标域（测试集）公共流行空间以适配分布及保持样本间结构的方法.公式如下：

根据多数非监督域适应方法的关键假设，不同域的边缘分布不同，即P≠Q，但预测分布却相同，即XT)［17］.式（5）中第一个范数即源域和目标域之间的最大均值差异（MMD），余下的范数累加求和表示同一域中样本之间的结构关系［22］.

2.4.1 联合优化

根据式（5），JLSDA算法可重新表示如下：

根据矩阵迹运算相关特性及之前的相关定义，式（6）可简化为

式（6）中第一部分与TCA域适应目标式类似［17］.式（7）中是核矩阵是MMD矩阵，都可以通过第一步迁移学习得到.记作且记作分别是源域和目标域的拉普拉斯矩阵，其中，和为源域和目标域的度矩阵和为源域和目标域的邻接矩阵.源域及目标域度矩阵对角线上元素分别为和分别为源域及目标域邻接矩阵的行列元素.为方便推导，式（7）可简化为

基于拉格朗日乘子法，问题（9）可重新表达为

其中，Z是包含拉格朗日乘子的对角阵.式（10）对W取导后并置0，可得

JLSDA算法的伪代码如算法2所示.

基于JLSDA算法得到变换矩阵W，进一步得到变换后的源域和目标域数据集，即变换后的源域为前n1个列向量构成，变换后的目标域为后n2个列向量构成.

3 结果

3.1 实验条件

3.1.1 数据集

本文使用了3 个语音数据集，有一定代表性.它们分别是TIMIT 公共语音数据集、Sakar数据集［4］和DNSH数据集.

第一个语音数据集作为第一步迁移学习的源域数据集.TIMIT 集总共包含6300 个句子，由630 个朗读者每人提供10 个句子，但目前只有240 个语音样本可用，40 名男性和40 名女性每人提供3 段语音.数据集扩展使用的噪声来源于NOISEX-9标准噪声集.

Sakar 数据集是PD 语音公开数据集，由Sakar 等人［7］提供，作为第一步迁移学习的目标域数据集.总共包含40 名受试者，其中20 名PD 患者（6 名女性，14 男性），20 名健康人（10 名女性，10 名男性），每人提供26个语音样本段，且每个语音样本段包含不同的发音内容，具体有连续的元音字母发音，数字发音，单词发音及短句发音.每个语音段都提取了26 个特征组成一个特征向量，包括频率类、振幅类、谐波类、基音频率等.

第3个数据集由本文作者自采，且受试者来自陆军军医大学第一附属医院.数据包含了未接受治疗的36名PD患者，其中16名女性（年龄的均值±标准差（mean±std）：57.9±9.0），20 名男性（mean±std：60.8±10.6）（患病时间的均值和标准差分别是7.38年和3.58年）；54名已接受治疗的PD 患者，其中27 名女性（mean±std：59.7±8.1），27 名男性（mean±std：63.2±10.8））（患病时间的均值和标准差分别是6.82年和3.50年）.每人提供13个语音段，每个语音段提取26个特征.

3.1.2 评价准则

为验证算法的有效性，本文使用分类准确率、灵敏度和特异度作为实验结果的评估准则.

根据数据集中一个受试者对应多个语音样本的特性，本文所提出算法使用LOSO（Leave-One-Subject-Out）交叉验证方法.分类器采用线性SVM，预测分类准确率累加再算数平均即得最终准确率.

3.1.3 实验平台

本文实验使用的计算机硬件配置为CPU（intel i3-4170M），6 GB memory，操作系统为64-bit Windows 7，实验运行在Matlab R2018b 版本上.论文参数设置如下.重复实验次数设置为10次，在第一步迁移学习中，主训练迭代次数、特征映射训练迭代次数及卷积核训练迭代次数分别为100，10和10，ADDM 缩放因子λ=1，松弛因子γ=1，卷积核数量从2 增加到8，尺寸为8*8.在第二步迁移学习中，正则化因子μ=0.01，核类型为‘rbf’，‘rbf’核宽度gamma 为100，关联矩阵模式为“simple”模式且最小邻居样本数为1.

3.2 两步式迁移学习算法的有效性验证

3.2.1 第一步迁移学习的有效性验证

以Sakar 数据集为例.在第一步迁移学习（FT）中，本文主要使用CSC 将TIMIT 的知识迁移到Sakar 数据集.本文尝试处理第一步迁移前后的数据，比较准确率差异.这里分类器选择KNN和SVM，分类结果见表1.

表1 基于Sakar集的第一步迁移学习分类准确率（LOSO）

如表1 所示，KNN 分类器的准确率为52.5%，优于SVM 分类器的50.0%.但是，经过第一步迁移学习之后分类准确率得到显著改善，FT&KNN 准确率为90%，FT&SVM 准确率为92.5%，灵敏度和特异度也明显提升.实验结果表明，FT 从公共语音集迁移到目标域的新增信息有助于目标域分类，其是有效的.

3.2.2 第二步迁移学习的有效性验证

以Sakar 数据集为例.在第二步迁移学习（ST）中，JLSDA 算法使训练集和测试集的分布差异减小，并保持原始结构信息.参照3.2.1 节，本文可通过比较迁移前后数据的分类准确率，来验证ST的有效性.请见表2分类结果.

如表2 所示，根据第二步迁移学习（ST）的实验结果，尽管性能提升程度不如第一步迁移学习（FT），但仍然有效.经过第二步迁移学习，基于KNN 准确率增加了15%，基于SVM准确率增加了12.5%.

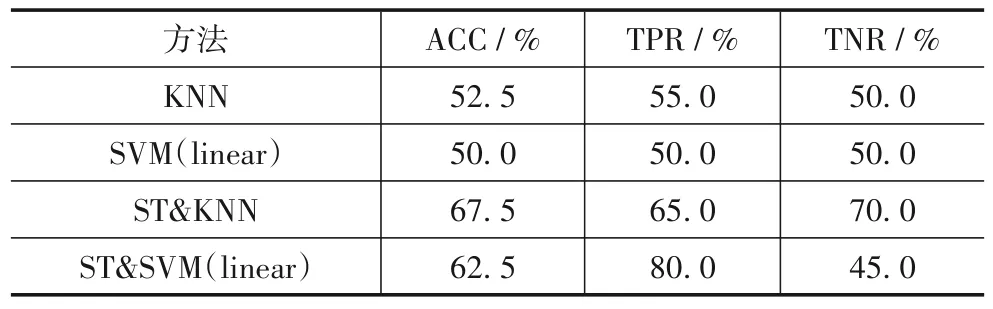
表2 基于Sakar数据集的第二步迁移学习分类准确率（LOSO）

3.3 算法比较

基于Sakar 数据集，本文选取了基于不同智能算法的代表性PD 语音诊断算法进行比较.文献［23］手动选择特征；文献［24］采用样本选择法，文献［25］是样本特征混合选择的代表；文献［26，27］均使用了倒谱系数；而文献［28］结合利用语音段选择，特征选择及神经网络等多种手段，且取得了相对更好的性能.此外，深度学习方法近年十分流行，因此本文选取了深度置信网络（Deep Belief Networks，DBN）、卷积神经网络（Convolutional Neural Network，CNN）、自动编码器（Autoencoder）算法，及SVM 和KNN 相结合的算法进行了比较.为验证迁移学习的效果，本文还选取了卷积稀疏编码迁移学习（Convolutional Sparse Coding Transfer Leaning，CSCTL）算法、经典域适应方法——迁移成分分析（Transfer Component Analysis，TCA）［27］结合SVM 分类器等一步式迁移学习算法，这些方法只单一考虑基于源域结构对目标域进行更有效表达或源域和目标域分布一致问题，通过比较证明，本文的两步式迁移学习在同时考虑上述两个问题后更有效.

表3显示了准确率比较结果.

表3 基于Sakar数据集的相关算法性能比较（LOSO）

如表3 所示，仅有小部分算法能达到90%的准确率.从方法论的角度看，深度学习并不比传统机器学习的效果更好，这也印证了深度学习依赖大样本量训练特性，并不适合PD 语音数据集这类小样本数据集.以上实验结果基于LOSO交叉验证.

如表4 所示，本文提出的算法在DNSH 数据集上也达到了较好的效果.与直接使用SVM 和KNN 分类器相比，本文提出的算法达到了90.63%的平均分类准确率，证明本文算法在中国人的PD 语音数据集上也十分有效.

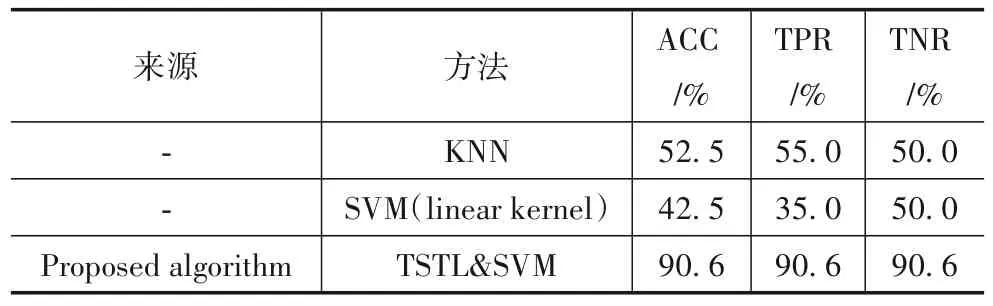
表4 基于DNSH数据集的相关算法比较（LOSO）

4 结论

虽然迁移学习可以解决PD 语音小样本问题，但面临不同数据集之间和训练集测试集之间的差异.为了解决这个问题，本文提出了一种新的解决方法——非监督两步式卷积稀疏迁移学习（TSTL）算法.实验结果表明，本文所提出算法的主要创新部分是有效的，在准确率、灵敏度及特异度上都较现有算法显著更好.

尽管本文算法被验证是有效的，但仍存在较大改进空间.下一步工作拟考虑结合不同大小和类型的公共语音数据集和各种代表性域适应方法，探索进一步提升本文算法性能的可能途径.