FAST望远镜主动反射面的理想形状*
胡嘉豪 , 蒋 沐 , 方 沙 , 刘成志
(湖南人文科技学院数学与金融学院,湖南 娄底 417000)
0 引言
2021年“高教社杯”全国大学生数学建模竞赛A题中,需要确定“FAST”望远镜主动反射面的理想抛物面使得其在接收天体电磁波时具有最佳接收效果。FAST是中国500 m口径球面射电望远镜(Fivehundred-meter Aperture Spherical radio Telescope)的简称,也称中国天眼。FAST是当今世界上单口径最大、灵敏度最高的射电望远镜。题目需要在反射面板调节约束下,确定一个理想抛物面,使其工作抛物面尽可能地贴近理想抛物面。
关于望远镜的工作原理有学者做了一些研究。早在2006年,陈忆就对FAST的主动主反射面进行了相关研究。通过理论分析和模型研究了每个单元球面块在望远镜跟踪过程中的抛物面的运动[1]。文献[2]根据FAST主动反射面的结构和工作原理,基于反射面单元动态面形精度分析,研究了FAST瞬时抛物面的拟合精度。文献[3]在缩小的射电天文望远镜模型上对FAST的主动反射面测量控制方案进行验证试验、分析,并给出了优化方案。文献[4]根据FAST反射面系统的要求及特点,提出了一个新的反射面结构体系方案——全球面整体张拉结构方案;并针对该结构体系给出目标位置成形分析的计算方法;最后采用支座位移法模拟FAST反射面由球面张拉拟合成抛物面的过程。文献[5]根据FAST主动反射面和馈源索支撑的方式,精确推导了主动反射面和馈源运动的数学方程,并分析了馈源节点的运动范围、速度和定位精度要求。文献[6]指出空域极化特性是焦径比和偏馈角的函数,并根据单偏馈抛物面天线设计中的约束设定了天线模型的参数。
本研究利用解析几何的相关知识,建立了主动反射面理想抛物面的数学模型,为后面问题的研究提供参考依据。
1 理想抛物面模型的建立
理想抛物面模型需要考虑反射面板调节等因素。首先需根据天体方位角与焦径比的关系确定抛物面中心点坐标,然后再建立理想抛物线的数学模型以确定理想抛物面的方程。
该问题涉及天体方位角与焦径比的关系公式,首先给出焦径比与辐射方向角的关系[7]:

其中,焦径比是指抛物面的焦距与口径之比,即:P/D1。P为抛物面的焦距,D1为抛物面在垂直于轴线的面上投影的口径直径。焦径比与馈源的方向角γ的关系如图1所示。
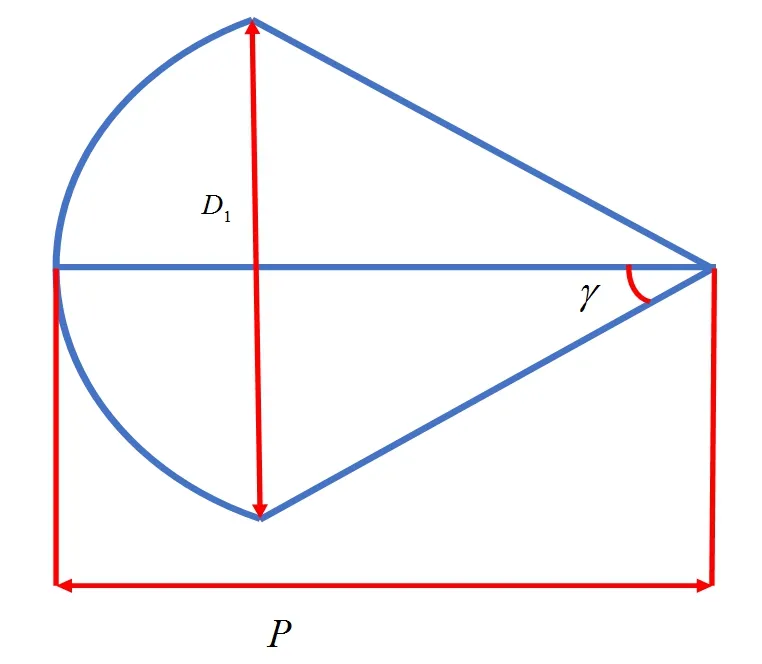
图1 焦径比P/D1与方向角γ的关系图
通过剖解FAST的主动反射面,得到剖面示意图如图2所示。图2中,记观测天体S到球心C的距离为SC,SC与工作抛物面边界的夹角为δ,馈源仓到工作抛物面口径中点的长度为L。从而可根据基准球面的半径R、口径D1与半径差F来求解SC与工作抛物面边界的夹角δ得到长度L,然后再求解方向角γ得到焦距P,据此写出抛物线方程后即可求解出理想抛物面方程。理想抛物面方程的求解流程如图3所示。

图2 α=0°、β=90°时主动反射面的剖面图

图3 理想抛物面方程的求解流程图
2 理想抛物面模型的求解
为了进一步求解抛物面的理想方程,首先以球心C为原点建立空间直角坐标系,如图4所示。

图4 以球心为原点建立的空间直角坐标系
根据题目中已知的数据,有基准球面球心C的半径R=300 m,F=0.466R,D1=300 m。题中说明了馈源舱所在的焦面与主动反射面为同一个球心。题目一中给出了α与β的角度,由题目中所给出的调节基准球面上的部分反射面形成以被观测物体到焦点的直线为对称轴,可以得出D1被直线CP平分,则有:

因此δ= 30°,于是:
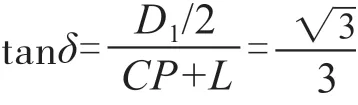
由题可知CP=R-F,从而:
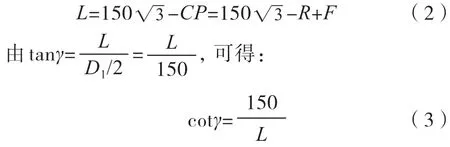
将式(2)和式(3)代入式(1)可得抛物面的焦距P=1.398 3×102。
设抛物线的标准方程y2=2px。根据文献[8-9]中关于抛物线焦点弦问题、抛物面的坐标变换、坐标轴平移、抛物面方程回归等一系列问题的研究可知,p为焦距P的两倍。理想抛物线应在z轴的负半轴,而由于观测天体方位角与仰角分别为:α=0°,β=90°。即观测天体位于主动反射面的正上方,所以抛物线的顶点将平移至基准球面最低点,从而理想抛物线的方程可写成:

这里的z0即为基准球面的最低点,即z0=300.033 9。
将焦距P和z0代入式(4)可得到主动反射面的理想抛物线方程:

由旋转抛物面知识[10],根据理想抛物线的方程可写出理想抛物面的方程:
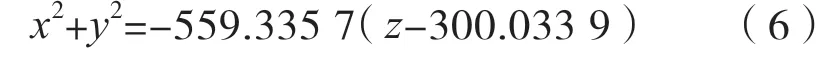
当观测天体方位角和仰角分别为α=0°、β=90°时,理想抛物面的三维立体图如图5所示。为了进行比较,根据题目所给的FAST基准球面的信息绘出其相应的三维立体图如图6所示。为了更清晰地进行对比,图7中将这两个三维立体图放入一个坐标系中进行比对,不难看出,理想抛物面与FAST基准球面的拟合程度较高。
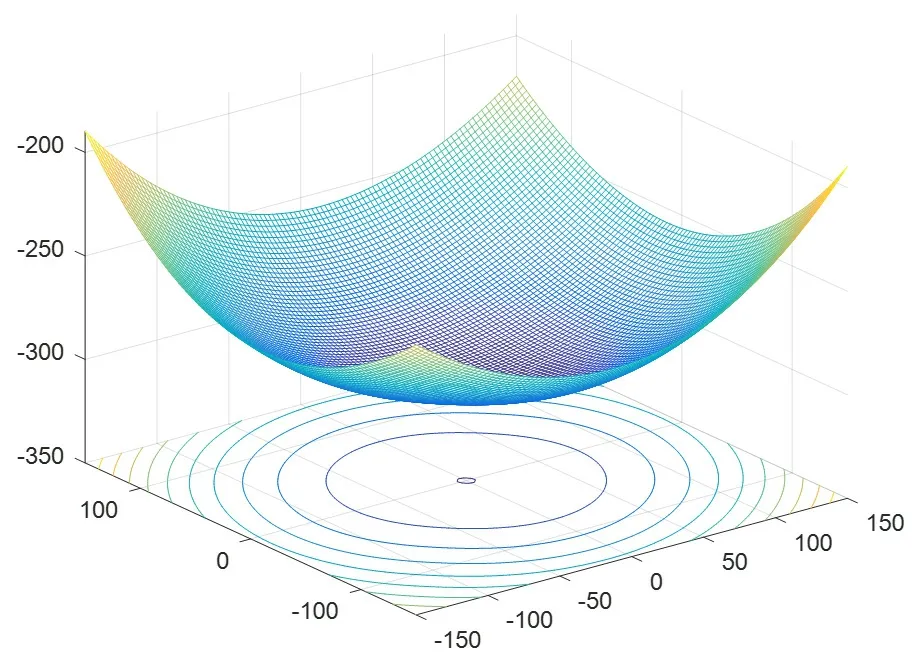
图5 α=0°、β=90°时理想抛物面的三维图
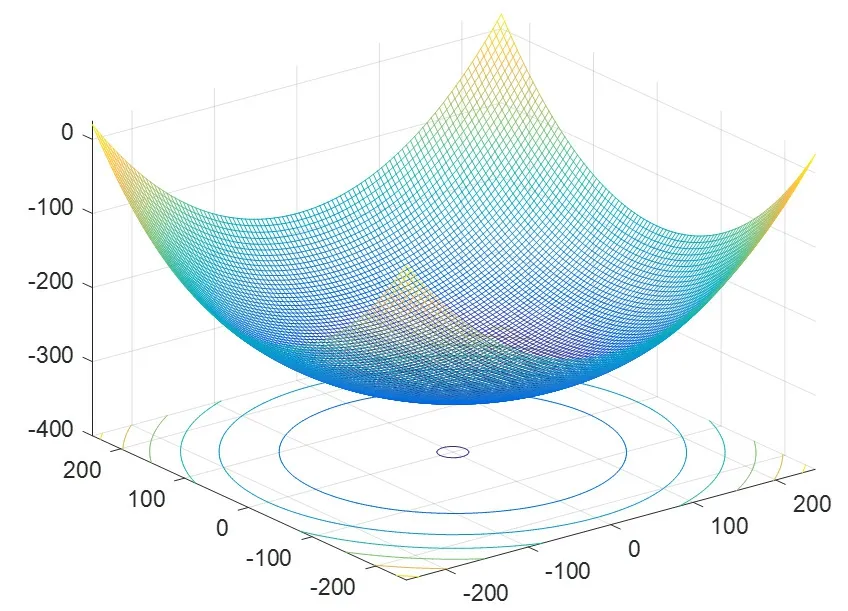
图6 基准球面的三维图
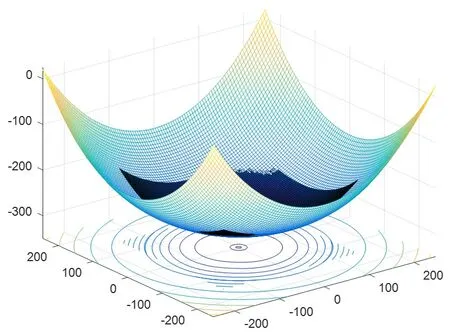
图7 在α=0°、β=90°的情况下理想抛物面在基准球面中的三维图
3 结论
为使得FAST望远镜在接收观测天体的电磁波时达到最佳效果,本研究通过分析FAST的剖解面,利用解析几何的知识探讨了当观测天体方位角和仰角分别为0°、90°时FAST 望远镜的主动反射面的理想形状。该模型计算方便,计算得出的理想抛物面较为精准。模型的提出为后续问题的求解打下基础。当然,关于理想抛物面的计算,还有其他方法。如文献[11]在没有焦距、焦径比的情况下,根据天体的仰角与方位角计算抛物线的焦距与焦径比。相比而言,本研究的计算方式容易理解且更为简单有效,求解得到的结果的准确度更高。

