基于Flowmaster的行星齿轮箱喷射润滑系统设计与分析*

王 翱 谭武中

(1.中南大学机电工程学院 湖南长沙 410083；2.中国航发湖南动力机械研究所 湖南株洲 412002)

行星齿轮箱具备结构紧凑、传动平稳、承载力大等特点，被广泛使用在医疗器械、交通运输、风力发电等领域[1]。而润滑系统作为齿轮箱不可或缺的部分，其性能将关系到齿轮箱工作的可靠性。常见的齿轮箱润滑方式有飞溅润滑、压力润滑、油雾润滑、强制润滑和喷射润滑[2]，对于转速高、空间狭小的旋翼飞机行星齿轮箱，喷射润滑是其首选的润滑方式。

近年来，国内外学者针对齿轮箱的喷射润滑展开了大量理论和实验研究。程江超[3]针对某齿轮箱的典型运行工况设计了润滑系统，并在分析了齿轮箱的功率、油压、温度等参数后筛选出合理的润滑系统元件。赵一帆[4]基于Fluent对某直升机主减速器的润滑系统进行了仿真研究，并对喷嘴计算公式进行了优化。徐斌等人[5]针对某车用变速箱内滚针轴承烧毁的现象，基于Particleworks软件进行仿真研究，并提出加长导油嘴的解决方案。李嘉东等[6]基于Flowmaster软件分析了某齿轮箱试验台润滑系统内节流元件的孔径及孔长对于压降的影响。张磊等人[7]通过Flowmaster软件建立润滑系统的液压模型并进行了模拟仿真和低温环境台架试验，对低温条件下齿轮箱润滑系统进行了改进设计。此外，张磊等人[8]建立了轴承和齿轮的功率热能模型，通过热平衡条件得出各润滑点的流量需求，并设计了相应的润滑系统管路。杨慧栋[9]设计了一款用于计算润滑系统主要参数的软件，并针对某齿轮试验台设计了相应的润滑系统，然后利用Flowmaster 软件对润滑系统进行了仿真与优化。赵昕等人[10]以风电齿轮箱为对象，利用Flowmaster 软件对其润滑系统进行了优化，研究结果表明，利用该软件可实现对润滑流量和压力的精确控制。卢元申[11]通过分析润滑系统流动计算的数理基础、减速器的物理结构、工作原理，建立了润滑系统的数学模型，并利用Flowmaster软件进行了稳态和瞬态的模拟仿真研究，将仿真结果和实验数据相比较，验证了仿真建模方法的可靠性。龙秀峰等[12]通过Flowmaster软件对某润滑系统内各部分的油压损失及管路流量进行了仿真分析，并与试验结果进行对比，验证了仿真方法的可行性。刘康[13]对某飞机重力供油系统进行了仿真分析，得到了不同工况下的支路流量及节点压力。针对狭小空间下润滑系统的流量分配，伍开松等[14]提出了“反求法”，按照约束级别的高低依次求出各管路直径，解决了管路尺寸受限时的流量分配问题。齿轮箱内的滑油需求量与生热情况密切相关，在这一方面，刘小刚等[15]针对轴承和齿轮的功率损失提出了不同的计算思路。在此基础上，靳国忠等[16]采用了稳态流体模型进行齿轮箱润滑系统的设计，并将结果与试验结果进行了对比验证。

目前，关于润滑系统的设计大多是首先基于经验公式进行计算与设计，再通过试验验证设计的可靠性以及进行相应的优化。这种方式的设计成本较高，而计算机的出现使得所设计润滑系统的可靠性可以通过模拟仿真来进行初步的验证，极大地降低了设计成本。基于此，本文作者首先结合齿轮箱内各润滑点的生热情况进行润滑系统的初步设计，之后通过Flowmaster软件对润滑系统性能进行稳态与瞬态仿真，验证了所设计润滑系统的可行性。

1 行星齿轮箱润滑系统设计

1.1 生热分析

行星齿轮箱由一个行星轮系组成，其运动简图如图1所示，由1个太阳轮、3个行星轮、内齿圈和行星架构成。其中，动力从太阳轮2输入，由行星架H输出，且内齿轮4被固定。齿轮箱工作时的额定功率为20 kW,额定转速为4 000 r/min，经过计算行星架相对于太阳轮的传动比i为5。

润滑的主要目的是减少摩擦副处的摩擦和带走系统内摩擦产生的热量，由弹性流体润滑理论发现，减少摩擦所需求的润滑流量相比散热可以忽略[17]，也即齿轮箱润滑系统的润滑油需求量取决于散热量大小。

齿轮箱内的热量包括齿轮、轴承等摩擦副内部产热和外部输入的热量。外部热量一般不能确定，多根据设计经验估计，内部摩擦副热量计算则是根据功率损失原理，由输入功率和输出功率之差计算得到，即认为摩擦副损失功率全部转化为产热功率[18]。

齿轮生热来自齿轮副的摩擦，可以通过齿轮副的功率损失计算得到。目前被广泛认可的齿轮功率损失计算方法是Anderson和 Loewenthal 方法，其将齿轮的功率损失分为滑动损失、滚动损失和风阻损失3部分，齿轮总的功率损失Pc为三者之和[19-20]。

滑动损失Ph来自轮齿啮合产生的摩擦力，与啮合面的平均法向载荷WN、摩擦因数f、平均滑动速度vs和滑动相关系数K1有关：

Ph=K1fWNvs

(1)

滚动损失Pr来自润滑油在轮齿啮合面被挤压形成的油膜，与油膜的厚度h、齿面宽度b、平均滚动速度vr、接触重合度mc和滚动相关系数K2有关：

Pr=K2hmcvrb

(2)

风阻损失Pw来自齿轮旋转和空气的摩擦，与齿轮的转速n、齿面宽度b、节圆半径D、润滑油黏度μ和齿轮旋转相关系数K3、K4有关：

(3)

(4)

轴承功率损失来自轴承滚动体和轴承滚道、保持架的摩擦，计算方法为Palmgren法[21]。轴承的摩擦力矩被分为关于载荷的摩擦力矩和与载荷无关的黏性摩擦力矩，轴承的损失功率Pz为两者引起的功率损失之和。如果轴承会承担轴向载荷，则会产生一个附加的摩擦力矩，其引起的损失功率也要考虑在内。

载荷引起的摩擦力矩Ml与轴承结构、相对负荷因数k1、轴承当量载荷Fβ、轴承的节圆直径dm有关：

Ml=k1Fβdm

(5)

黏性摩擦力矩Mn与轴承类型、润滑方式因数f0、润滑油运动黏度ν0、轴承转速n、轴承的节圆直径dm有关：

(6)

圆锥滚子轴承附加的摩擦力矩Ma与润滑方式因数k2、轴向力Fa、轴承的节圆直径dm有关：

Ma=k2Fadm

(7)

Pz=1.047×10-4(Ml+Mn+Ma)n

(8)

系统的总生热量为各摩擦副的生热量之和，考虑到箱体对流散热，润滑系统需要带走生热量的90%。采用比热容为Cp、密度为ρ的润滑油，在系统温度变化不大于ΔT时系统润滑油需求量Qg计算公式如下：

(9)

文中润滑系统选用润滑油动力黏度为17 mPa·s，比热容为2.05 kJ/(kg·℃)，润滑油密度为0.99 g/mm3。设定系统内温度变化不超过30 ℃，计算后可得各润滑点的滑油需求量。

1.2 喷嘴参数设计

喷嘴的作用是向摩擦副喷射润滑油，其喷射量取决于喷油速度、喷嘴直径等因素。一般地，齿轮箱所用的喷嘴喷孔属于厚壁孔，供油压力决定喷嘴的喷射速度，通常为0.24～0.48 MPa之间。则喷射速度vp的计算方法为

(10)

式中：CV为喷嘴的流速系数；p0为环境的空气压力；ρ为润滑油的密度。

根据系统需求设定每个摩擦副处的喷嘴个数以及单个喷嘴的供油流量Qi，则每个喷油孔的孔径为

(11)

d的推荐取值为0.8～2.5 mm，如不符合则需要重新确定喷嘴个数及单个喷嘴供油流量。

1.3 油管参数设计

油管的作用是输送润滑油，其布置方式需要考虑喷嘴的位置和齿轮箱的结构、尺寸。在设计时管路的直径D可以根据下式计算：

(12)

式中：v为润滑油在油管中的流动速度(m/s)；Q为油管中的润滑油流量(L/min)；D为油管直径(mm)。

油管中润滑油的流动速度存在最大值——许可流速，许可流速受到系统压力影响，其关系如表1所示。

表1 管路许可流速

1.4 管路布置

文中共有5处不同类型的润滑点，分别是太阳轮轴承、行星轮轴承、输出轴轴承、太阳轮和行星轮啮合处、行星轮和内齿圈啮合处。按照距离和润滑管路布置的方便程度可以将其分为3部分：第一部分对太阳轮处轴承供油；第二部分对输出轴轴承供油；第三部分对太阳轮和行星轮啮合处、行星齿轮和内齿轮啮合处、行星齿轮处轴承供油。管路布置如图2所示，其中1～11代表润滑点，G1～G16代表管路。各部分管路及喷嘴的尺寸根据上文所述方法来确定。

2 润滑系统仿真模型的搭建

为确保润滑系统能够满足系统的润滑需求，需要对其进行验证。传统的方法是搭建相应的试验台进行试验验证，但其成本较高，不利于后期的设计优化，而通过仿真可以有效解决这一问题。文中选择Flowmaster软件来进行相应的仿真计算。

润滑系统主要由喷嘴、管路、阀门、油泵和过滤器等部件组成，在Flowmaster软件中选择合适的组件,搭建润滑系统的仿真模型如图3所示。

在模型的建立过程中，对系统进行一定的简化是必不可少的。主要涉及以下几个方面的假设与简化：

(1)管路密封得当，不存在润滑油的泄漏。

(2)忽略重力的作用。齿轮箱结构比较紧凑，润滑系统中的油管布置也比较紧凑，在高度上没有大的变化。因而在润滑油的流动过程中重力的影响可以不考虑。

(3)忽略润滑系统元件的热交换。由于文中设计重要的指标是压力、流量，模型仿真就是为了研究它们的变化情况，系统中器件的热交换不是主要因素，不在考虑范围内。

(4)忽略管路连接处的流动损失。弯头、过渡接头都属于低流阻元件，由于它们产生的流动损失比较小，和较长的直管中产生的流动损失相比几乎不存在，根据实验证明可以忽略。

(5)使用离散损失模型替代众多流动阻力元件。在保证替代前后系统局部的流动阻力-流量曲线不变的情况下，该替代不仅不会带来大的误差，还能节约仿真计算时间。

3 仿真分析

3.1 稳态仿真

稳态性能仿真可以检验润滑系统设计的合理性。将润滑系统的各参数输入软件中，选择不可压缩稳态仿真，得到各润滑点处的流量值如表2和图4所示，喷嘴压力和速度分别如图5和图6所示。

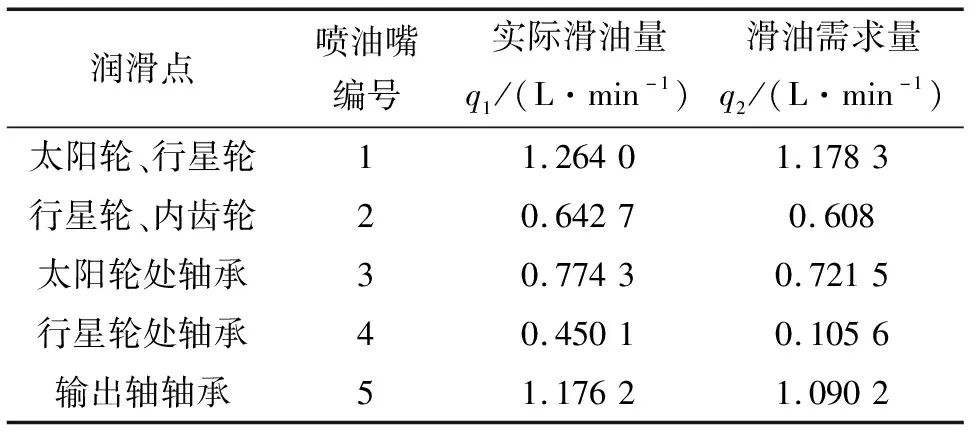
表2 润滑点滑油实际流量与需求量对比

分析表2和图4发现，主油管G1实际流量为10.75 L/min，略大于需求量。各处润滑点实际润滑量也都大于需求量，这是因为在系统设计时留下了1.2倍的裕度。经过核算后发现，各点显示的差值除4号位置外均是由于裕度产生，都在合理范围。

4号位置为行星轮轴承处的喷嘴，实际流量超出需求量3倍以上。原因是设计时该处滑油需求量过小，喷嘴布置时孔径小于推荐值，故而进行了扩大，对喷孔孔径的扩大带来了大的流量误差。

分析图5和图6发现，喷嘴压力均在0.3 MPa以上，符合要求。喷嘴的喷油速度均符合要求，能够达到20 m/s。

3.2 瞬态仿真

在稳态性能满足条件后，需要考虑润滑系统的瞬态性能。当阀门状态发生变化时，系统的压力会随着改变。尤其是在阀门关闭的过程中，系统的压力会急剧变大，该压力变化可能会对系统元件造成破坏。根据不同的阀门关闭速度可以进行不同的瞬态测试。

3.2.1 压力波动分析

由于阀门关闭速度会影响到压力波动，故需要考虑阀门关闭耗费的时间。0～1 s时设置阀门为全部开度状态，分别考虑从1 s后将阀门在不同的时间内完全关闭，可以得到阀门前端节点不同的压力实验数据。如图7所示。

分析图7可知，当阀门在0.4 s左右关闭时系统基本没有冲击现象的发生，故阀门关闭时间必须大于0.4 s。在实际的润滑系统元件选型中，为了安全必须选择闭合时间大于0.4 s的阀门。

3.2.2 流量波动分析

各润滑点喷嘴的压力、流量会随着阀门的关闭发生变化。虽然各喷嘴在布置位置、孔径上存在的不同会使得它们在阀门关闭时受到的影响有差异，但是其主要变化趋势是一样的。因此，文中研究一个喷嘴的流量响应、压力响应情况来替代研究所有喷嘴在阀门关闭后的响应情况，以此来说明喷嘴在阀门关闭后的流量、压力等特性的变化情况。

分析图8可知，喷嘴流量会随着阀门的关闭而减小，这与阀门关闭的速度无关，阀门关闭时间不影响最终的流量减少趋势。在阀门关闭的瞬间，喷嘴流量会发生波动，且并不是直线减小，在某个短暂瞬间甚至会出现负值。流量波动大小与阀门关闭时间相关，阀门关闭时间越大，流量波动越小。

分析图9可知，喷嘴处的压力变化和流量变化有一样的趋势。原因主要是阀门关闭后，喷嘴压力减少快速，导致喷嘴出现负压，此时喷嘴就会出现流量的负值，润滑油发生回流。而由于喷嘴流量负值的出现，喷嘴内压力又会上升，润滑油也变为正向流动。如此循环往复直至趋于稳定。

对喷嘴处流量、压力波动的分析再次说明阀门关闭速度不能过大，否则会影响系统安全性能，推荐选择关闭时间超出0.4 s的阀门。

4 结论

(1)对某行星齿轮箱润滑系统的生热情况进行分析，得到齿轮及轴承摩擦副的功率损失，发现输入齿轮处的摩擦生热量最大，滑油需求量也相应最多。根据各润滑点的滑油需求量对油管及喷嘴的布置与尺寸进行计算。

(2)在Flowmaster中建立润滑系统的仿真模型，稳态仿真结果表明，各喷嘴处的滑油需求量、喷嘴压力与喷射速度均满足设计需求。

(3)阀门的关闭速度会影响系统的流量和压力特性，Flowmaster瞬态仿真结果表明，设置阀门的关闭速度大于0.4 s可以有效减轻阀门关闭时带来的系统压力和流量的波动。