中欧规范钢-混组合梁抗弯承载力计算方法对比
暨邦冲
(福建工程学院 土木工程学院,福建 福州 350118)
钢-混凝土组合梁(以下简称组合梁)。通过剪力连接件将钢梁和混凝板组合成整体共同受力,充分发挥钢材受拉、混凝土受压性能好的优点。与钢梁相比,组合梁截面刚度大,可减小梁的挠度,还可提高梁的自振频率;与混凝土梁相比,组合梁结构自重小,结构高度低,吊装重量轻,在国外应用较为广泛[1-3]。
目前国内外已经颁布一些组合梁的设计规范,如我国颁布的GB 50917-2013《钢-混凝土组合桥梁设计规范》[4]、GB 50017-2017《钢结构设计标准》[5]和JGJ138-2016《组合结构设计规范》[6],以及欧洲规范EUROCODE 4(简称EC4)[7]。上述规范中的计算方法和理论分析各异,可靠度水准也参差不齐[8]。
为探讨上述规范的计算精度,本文在收集组合梁试验研究资料的基础上,分别采用中国规范GB 50017-2017、JGJ138-2016、欧洲规范EC4及线弹性法,计算所收集试件的抗弯承载力,并与试验结果进行比较,分析不同规范之间在计算精度方面的差异,为组合梁的结构设计提供参考。
1 现各规范的计算方法
1.1 GB 50917-2013
GB 50917-2013采用塑性设计方法计算组合梁的抗弯承载力,计算时根据塑性中和轴的位置,将截面分为两种类型。
1.1.1 塑性中和轴在钢梁内
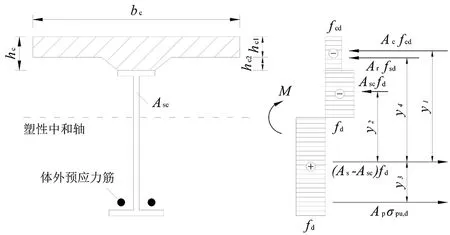
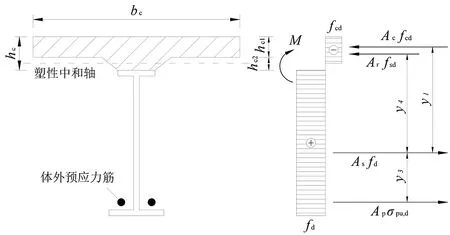
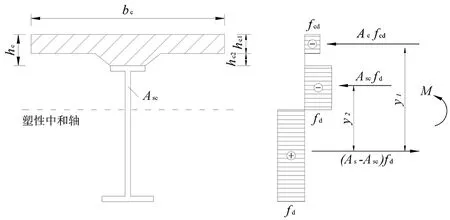
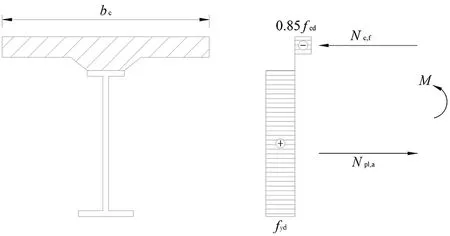
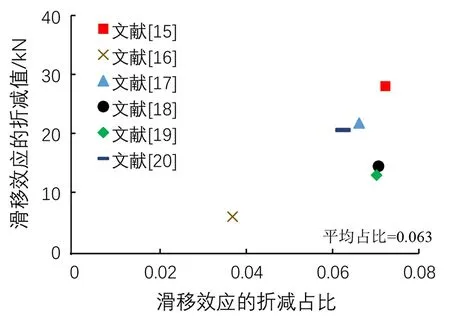
即满足公式Acfcd+Arfsd γ0M≤k(Acfcdy1+Ascfdy2+ Apσpu,dy3+Arfsy4) (1) (2) k=1-0.048e-0.43r (3) (4) 图1 塑性中和轴在钢梁内时的应力图形 1.1.2 塑性中和轴在混凝土桥面板内 即Acfcd+Arfsd≥Asfd++Asσpu,d时,抗弯承载力应符合下列公式要求: γ0M≤k(Accfcdy1+Apσpu,dy3+Arfsdy4) (5) (6) k=1-0.082e-0.3r (7) 式中:Ace为塑性中和轴上侧混凝土桥面板的面积,mm2;bc为混凝土桥面板的有效宽度,mm;x为混凝土桥面板受压区高度,mm;k为考虑滑移效应的拟合系数,取0.94,也可用式(7)计算。 图2 塑性中和轴在混凝土桥面板内时的应力图形 单个栓钉连接件的抗剪承载力设计值取式(8)和(9)中的较小值。 (8) (9) 式中,Astd为栓杆的截面面积,mm2;Ec、Es为混凝土和栓钉的弹性模量,MPa;fcu为混凝土立方体抗压强度,MPa;fstd栓钉的抗拉强度,MPa;η为群钉效应折减系数。 组合梁也有剪力滞,但剪力滞分析计算较为复杂[9-10],故各规范中均引入有效宽度进行简化计算,且计算方法也各有不同。 GB 50917-2013参考了EC4中关于组合梁有效宽度的相关规定,其规定组合梁桥面板的有效宽度bc应符合下列规定: (1)中间跨和中间支座的有效宽度bc按下列公式计算: bc=b0+∑bei (10) (11) (2)边支座的有效宽度按下列公式计算: bc=b0+∑βibei (12) βi=(0.55+0.025Le/bei)≤1.0 (13) 式中:b0为同一截面最外侧抗剪连接件间的横向间距,mm;bei为钢梁腹板一侧的混凝土桥面板有效宽度,mm,且不应超过板的实际宽度bi;Le为组合梁的有效跨径。 GB 50017-2017与JGJ138-2016中关于组合梁的计算方法与原则完全相同。对于完全抗剪连接组合梁的正弯矩验算,GB 50017-2017与JGJ138-2016也根据塑性中和轴的位置,将截面分为两种类型: 1.2.1 塑性中和轴在混凝土翼板内 即Asfd≤bchc1fcd时,受弯承载力应满足下式: M≤bcxfcdy (14) (15) 式中,x为受压区高度,mm;y为钢梁截面至混凝土受压区截面间的应力合力距离,mm。 图3 塑性中和轴在混凝土翼板内时的应力图形 1.2.2 塑性中和轴在钢梁截面内 即Asfd>bchc1fcd时,受弯承载力应满足下式: M≤bchc1fcdy1+Ascfdy2 (16) Asc=0.5(As-bchc1fcd/fd) (17) 图4 塑性中和轴在钢梁内时的应力图形 由以上公式可看出,GB 50017-2017与JGJ138-2016的计算方法忽略了混凝土板中纵向钢筋对于承载力的贡献,且不考虑滑移效应,也不考虑栓钉的纵向布置对结构承载力的影响。因此计算所需确定的参数少,公式简洁,计算过程快。 GB 50017-2017、JGJ138-2016GB与GB 50917-2013计算方法的主要差异是:GB 50917-2013考虑了混凝土板中纵向钢筋对于承载力的贡献,并考虑栓钉布置对于滑移效应影响,采用系数k对最后计算出的抗弯承载力进行折减。但若要精确计算滑移效应,所需计算的参数较多,计算过程繁琐。在本文介绍的若干规范中,仅有GB 50917-2013的计算方法考虑了布有体外预应力筋的情况,其它规范均未考虑。 对于有效宽度的计算,GB 50017-2017与JGJ138-2016中的条文规定仍然相同:在进行组合梁截面承载能力验算时,跨中及中间支座处混凝土翼板的有效宽度bc应按下式计算: bc=b0+b1+b2 (18) 式中:b0为板托顶部的宽度,mm;b1、b2为梁外侧和内侧的翼板计算宽度,mm,各取梁等效跨径le的1/6,且b1尚不应超过翼板实际外伸宽度S1,b2不应超过相邻钢梁上翼缘或板托间净距S0的1/2。 GB 50017-2017与JGJ138-2016中有效宽度的计算,参照了EC4的相关条文并结合相关研究成果,主要还是考虑以梁跨径为影响有效宽度的主要因素,取消了旧规范GB 50017-2003[11]中有效宽度与厚度相关的规定,实际上也有试验与理论分析表明[12],板厚对有效宽度影响很小。 EC4中规定,根据不同的结构形式,可采用塑性理论、弹性分析理论和非线性理论等不同计算方法与理论。限于篇幅,本文采用EC4中的塑性计算理论进行对比,EC4中也给出了典型塑性应力分布图(见图5)。图中,fyd为纵向钢筋设计屈服强度,fcd为混凝土圆柱体抗压强度设计值。具体计算公式参见文献[13-14]。 图5 组合梁塑性应力分布示例图 在EC4中,根据塑性中和轴所处的位置,将结构分成塑性中和轴在混凝土板内、塑性中和轴在钢梁的受压翼缘中和塑性中和轴位于钢梁腹板中3种情况计算截面的受弯承载力。 对于有效宽度,EC4中的计算方法与GB 50917-2013中的方法类似。不同点为,EC4中混凝土桥面板有效宽度bei取Le/8,而GB 50917-2013取Le/6,其余的公式均一致。另关于有效跨径Le,两个规范在系数大小上的取值也略有不同。 因此,EC4的计算方法可以说是介于另两种方法之间,有效宽度的计算方法与GB 50917-2013相似,同样不考虑纵向钢筋对承载力的贡献以及滑移效应和栓钉纵向布置的影响。 此外,与我国规范的主要差别在于对混凝土强度的取值,EC4中规定受压混凝土的有效面积承受0.85fcd的应力,乘以0.85是为了消除结构中混凝土强度与试件混凝土强度间差异的影响。在乘以0.85修正后,EC4中混凝土板对抗弯承载力的贡献比我国规范的略高一些,比我国常用的C40~C60混凝土,会高出1%~10%。 线弹性法是较为经典的计算方法,在各国规范中均有提及,例如EC4,以及我国的JTG D64-2015《公路钢结构桥梁设计规范》和JTG/T D64-01-2015《公路钢混组合桥梁设计与施工规范》等,但各规范有效宽度的计算规定略有不同。限于篇幅,这里以JTG D64-2015与JTG/T D64-01-2015方法为例进行讨论。 JTG D64-2015与JTG/T D64-01-2015中规定,组合梁抗弯承载力应满足下式: (19) γ0σ≤f (20) 式中,i为变量,表示不同的应力计算阶段;Md,i为不同应力计算阶段作用于钢梁或组合梁截面的弯矩设计值,N·mm;Weff,i为不同应力计算阶段钢梁或组合梁截面的抗弯模量,mm3;f为钢筋、钢梁或混凝土的强度设计值,MPa。 JTG D64-2015和JTG/T D64-01-2015有效宽度的计算方法与GB 50917-2013一致。 从文献[15-20]中收集6根不同构造组合梁的受弯试件进行分析,所有试件均为简支梁,试件基本参数如表1所示。 表1 试件参数表 根据前文所提到的各规范中有效宽度的计算方法,由表1中各试件的参数,计算各试件的有效宽度。计算结果如表2所示。 表2 有效宽度计算结果表 由结果可知,EC4对于有效宽度的取值明显保守于其它规范,即更容易使有效宽度产生折减。尤其是对于只布置单个抗剪连接件或混凝土翼缘长度较长的构件[18,20],采用EC4中的计算方法对有效宽度折减影响较大。 根据前文提到的计算方法,计算上文中各试件的极限抗弯承载力,并与实测值对比。对于GB 50917-2013中滑移效应的拟合系数k,不使用规范推荐的经验值,采用规范中的公式计算;对于线弹性法,判定构件达到极限承载力的条件是型钢达到屈服强度或混凝土达到极限压应力。 表3为按各规范计算方法计算出的中性轴位置。由结果可看出,各规范计算出的塑性中性轴的位置均相同,未出现不一致现象。 表3 塑性中性轴所在位置统计表 按各规范的方法计算构件抗弯承载力的结果如图6所示,从图6可看出,不同计算方法计算出的试件抗弯强度荷载理论值与实测值之间存在一定的差异。从计算结果看,GB 50017-2017与JGJ138-2016计算结果平均值较为接近1,为0.969,即计算荷载值更接近实测值,其变异系数也较低,为0.093,说明数据离散性较小,计算结果较为稳定;EC4计算结果平均值略低于GB 50017-2017与JGJ138-2016,为0.967,相差不大,但标准差与变异系数比前两种方法大,说明数据离散性较大;GB 50917-2013计算结果平均值较低,说明计算荷载值与实测值相差较大,该方法较为保守;线弹性法的平均值为所有方法中最低,说明计算荷载值与实测值相差偏大,且标准差与变异系数为4种方法中最大,说明数据离散性偏大。 图6 组合梁抗弯承载力计算值与试验值的比较 从图7中的计算结果数据分布来看,采用塑性理论的3种方法几乎所有数据点均位于45度线y=x附近,整体呈平行分布,说明其在不同的构造参数下都能保持较为良好的精度,但线弹性法数据点偏离直线y=x较多。GB 50917-2013计算方法的数据点除文献[19]外,其余数据点均位于45度线y=x的上方,说明大部分构件计算荷载值均小于实测值,采用其方法计算能够给予构件一定的安全储备,对于位于直线y=x下方的文献[19]数据点,其计算荷载值与实测荷载值之比为1.075,误差较低,采用该方法较为保守;GB 50017-2017与JGJ138-2016计算方法的数据点除文献[19]及文献[20]外,其余更加靠近直线y=x,且均位于直线上方,说明采用此方法,在有一定安全储备的同时,计算荷载值与实测荷载值也较为接近,对于位于直线y=x下方的文献[19]与文献[20]数据点,其计算荷载值与实测荷载值之比分别为1.131与1.012,说明该方法在计算文献[19]此类结构时,误差较大,但是计算其它类型的结构精度较高;EC4计算方法的数据点与直线y=x靠近程度介于以上两种方法之间,但是采用该方法计算文献[16]与文献[19]的结构,其计算荷载值与实测荷载值之比分别为1.131与1.008,总体与GB 50017-2017和JGJ138-2016的计算结果相似;线弹性法为3种方法中最保守的,除文献[20]的构件外,其余均位于y=x上方,说明该方法有较大的安全储备,但整体误差大,对于文献[20]的构件,其计算荷载值与实测荷载值之比为1.001,实际采用线弹性法时,会取用较高的安全系数,使得该方法进一步偏向保守,造成材料浪费。 图7为采用GB 50917-2013的计算方法计算时,不考虑滑移效应折减,即按公式(1)或(5)计算,但去除公式中考虑滑移效应的拟合系数k。计算结果平均值为0.982,比考虑滑移效应及其它规范的结果更接近1,变异系数也略微降低,说明去除滑移效应的拟合系数k后,计算荷载值更接近实测值,数据离散性也更小。 图8为采用GB 50917-2013的计算方法计算时,考虑滑移效应对承载力的折减占比。滑移效应对承载力的平均折减率为6.3%,即平均折减系数k为0.937。本次计算的试件中,仅有文献[16]的塑性轴位于钢梁,计算出的折减系数值为0.963,即折减率为0.037;而其余6个试件的中性轴都位于混凝土板,其计算出的折减系数平均值为0.932,即折减率为0.068。计算得出的折减系数分别与规范推荐经验值0.96与0.94差别较小。 图8 GB 50917-2013方法中考虑滑移效应的折减占比 图9为采用GB 50917-2013的计算方法计算时,纵向钢筋对承载力的贡献(不考虑滑移效应的折减),另两种采用塑性理论规范的计算方法均未考虑纵向钢筋对抗弯承载力的贡献。纵向钢筋的平均值为10.3%,说明纵向钢筋对抗弯承载力有一定贡献。文献[19]与文献[20]的构件混凝土板配筋率较高,故纵向钢筋对总承载力的占比较高,分别为14.27%与15.63%。 图9 纵向钢筋对抗弯承载力的贡献 综上所述,使用GB 50017-2017与JGJ138-2016的计算方法计算出的理论值较其它3种计算方法更为接近实测值,且稳定性最好。当考虑需要一定安全储备时,也可采用较为保守的GB 50917-2013计算方法。在设计较为重要的结构时,建议额外采用线弹性法进行校核。 (1)GB 50017-2017与JGJ138-2016的计算公式较为简洁,但该方法在计算文献[19]这类构件时,由于该构件混凝土翼板较宽、钢梁上翼缘宽度较小、钢梁与混凝土板连接件采用单排连接件,且有效宽度未折减,导致计算出的承载力偏高。文献[18]与文献[19]构件基本相同,但文献[18]构件钢梁上翼缘宽度大,导致计算结果较为保守。建议在计算类似于文献[19]的构件时,采用GB 50917-2013的方法。 (2)GB 50917-2013的计算方法考虑了混凝土板中纵向钢筋对于承载力的贡献,相对于其它两种计算方法,原本应使计算值更大,但是考虑滑移效应的拟合系数k后,结构最终的承载力折减较大,因此计算值偏于保守。对于混凝土板配筋率较高、混凝土翼板较宽、钢梁上翼缘宽度较小、钢梁与混凝土板连接件采用单排连接件的构件(如文献[19]),纵向钢筋对总抗弯承载力的贡献较大,且滑移效应的不利影响较明显,两者均不宜忽略,故采用该方法计算精度较好。但该公式较为繁琐,建议实际计算时,考虑滑移效应的拟合系数k直接取规范所推荐的经验值。 (3)EC4的计算方法与GB 50017-2017和JGJ138-2016相似,在计算类似于文献[19]的构件时误差较大,而精度与稳定性介于另两种采用塑性方法的规范之间。EC4的有效宽度折减较为严格,使得在计算部分构件时其结构比GB 50017-2017与JGJ138-2016的结果更偏向于保守。另由于我国与欧洲计算时选用的混凝土标准强度不同,导致按其方法计算时混凝土板对抗弯承载力的贡献会比我国规范的略高一些。 (4)线弹性法的计算过程较为简单,但计算结果为所有方法中最保守,且在实际计算时,规范本身的设计值已做折减,另还需要考虑安全系数,使得按线弹性法的结果进一步偏向于保守,按线弹性法设计的构件材料容易造成浪费。 1)采用塑性理论的GB 50917-2013、GB 50017-2017、JGJ138-2016与EC4中抗弯承载力的计算方法,主要的不同在于有效宽度的计算、是否考虑滑移效应的影响与是否计入纵向钢筋对抗弯承载力的贡献。 2)由于现有研究在试件参数、具体构造及选用理论的差异,本文提及的4种计算方法的计算结果与实际得到的试验值都存在一定的偏差,相对而言,GB 50017-2017与JGJ138-2016的计算方法得到抗弯承载力的计算理论值与试验实测值更加接近,且数据更为稳定。但采用此方法计算钢与混凝土连接较弱、混凝土板较宽且钢梁上翼缘宽度较小的构件时,会使计算理论值高于试验实测值,导致结果偏不安全。 3)GB 50917-2013考虑了纵向钢筋对于承载力的贡献与整体栓钉布置导致的滑移效应,使得混凝土板中纵向钢筋配筋率较高时,采用该方法精度较好。但是该方法中考虑滑移效应后对最后计算出的抗弯承载力折减较大,使得该方法计算出的结果较为保守。 4)EC4的有效宽度折减较为严格,使得在计算部分构件时其结构比GB 50017-2017与JGJ138-2016的结果更偏向于保守,而精度与稳定性则介于另两种采用塑性方法的规范之间。但是由于我国与欧洲计算时选用的混凝土标准强度不同,导致按其方法计算时混凝土板对抗弯承载力的贡献会比我国规范的略高一些。 5)线弹性法比塑性理论更为保守,建议仅在设计较为重要的结构,额外地采用线弹性法进行校核,或规范规定不能采用塑性理论时再采用该方法。
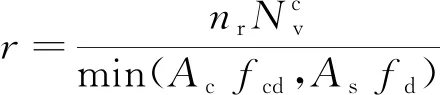




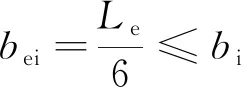
1.2 GB 50017-2017与JGJ138-2016


1.3 EC4
1.4 线弹性法

2 计算方法比较与分析

2.1 有效宽度的比较
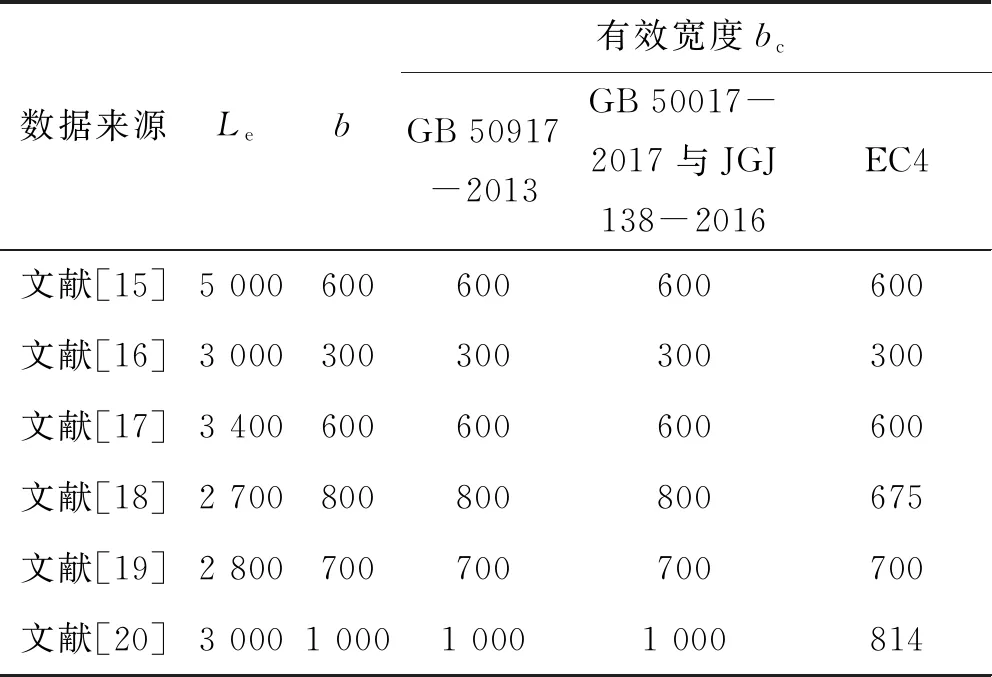
2.2 计算值与试验值的比较

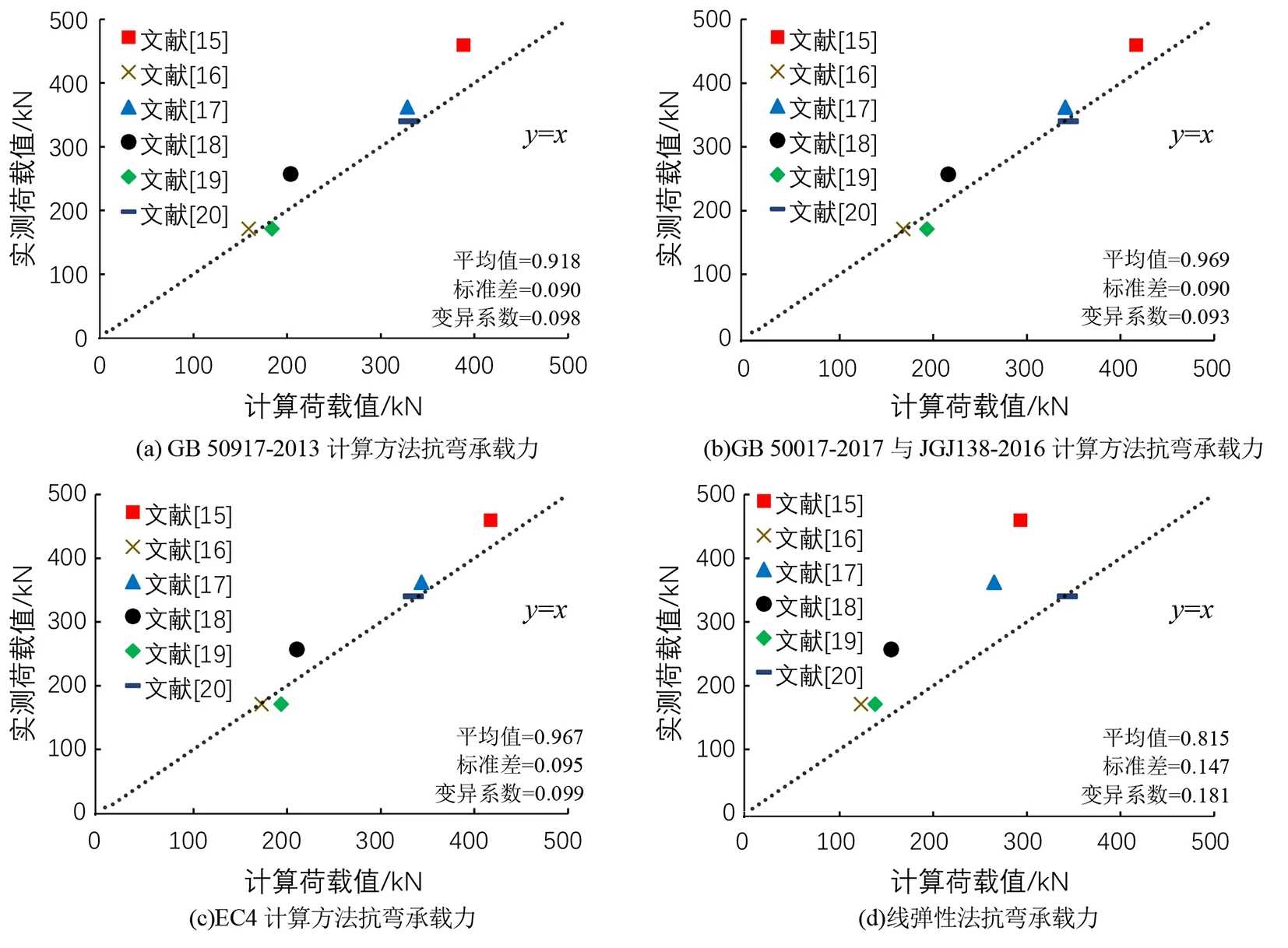

2.3 计算方法分析
4 结论

