重载交通路段的桥梁汽车荷载效应评估

张玮

(1. 福建省建筑工程质量检测中心有限公司，福建 福州 350028；2. 福建省绿色建筑技术重点实验室，福建 福州 350001)

近三十年来我国道路交通运输产业持续呈现爆发式发展，据统计[1]，我国2020年末拥有公路载货汽车1 110.28万辆、载货重量15 784.17万吨位，平均每辆车载货14.22 t，相对于2019年末的12.49 t/辆增加了13.9%。此外，不同区域的货物运输水平具有显著差异的特征，导致道路运输的货车重载超载问题愈加复杂[2]。

重载货车对于交通基础设施安全特别是道路运输网络中的桥梁结构有显著的威胁，多起桥梁垮塌事故都是由超载重载货车作用引起的[3]。大量研究表明我国当前的运输荷载显著超过桥梁设计规范预期，刘少辉等[4]通过布设在福建省内两个典型重载交通路段的动态称重(weigh in motion, WIM)系统采集数据，建立了适用于福建省公路桥梁疲劳寿命分析的汽车荷载模型。周军勇等人[5]基于我国高速公路采集的两车道、三车道和四车道WIM数据，分析了横向车道荷载及货车流量的差异，并分析了差异化车道荷载作用下的车道荷载效应及其引起的结构疲劳，研究表明横向车道上的极值荷载效应与等效荷载效应均存在显著差别，但目前规范体系并没有考虑对这一特性做修正。李占峰等[6]调查了京港澳高速河北省内的WIM数据并建立了重车荷载模型，将实际采集重车作用下的T梁荷载效应与规范计算结果对比，结果表明实际货车荷载效应达到规范计算的1.2～1.4倍，当前规范汽车荷载模型低估了实际重载货车产生的荷载效应。颜全哲等[7]基于福建省内采集的WIM数据分析了实际货车作用下的桥梁荷载效应，结果表明规范公路I级荷载标准能够涵盖实际货车作用下的荷载效应，但是公路II级偏于不安全。综上可知，为了掌握货车作用下桥梁的结构安全性，需要采集实际车辆荷载数据并开展随机车流荷载效应分析，评估桥梁荷载效应与规范荷载模型计算结果的关系，为荷载管理及桥梁健康监测提供参考。

本研究依托某公路桥梁采集的16个月WIM数据开展研究，该桥为预应力混凝土简支梁桥，跨径布置3×28 m，桥宽9 m承载双向两车道，公路II级设计荷载，修建于2010年，结构布置如图1所示。该桥在最近一次的检测中评定为总体技术状况等级2类，结构基本完好，对使用状态无影响。该桥桥头安装了一套WIM系统，系统布置图如图2所示。该桥路段长期承载重载运输货车，主要服务周边采石场及采砂场，这种重载运输路段具有普遍代表性，但是由于公路等级低而管养资源有限，因此这些桥梁在重载货车作用下的效应评估尤为重要。

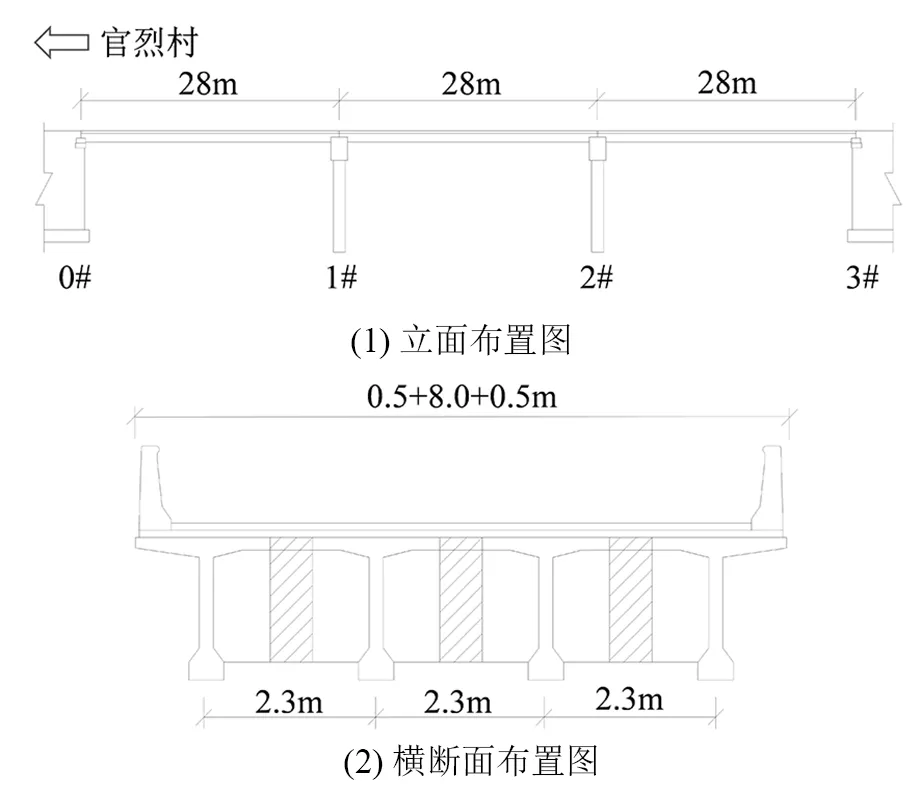
图1 桥梁总体布置图

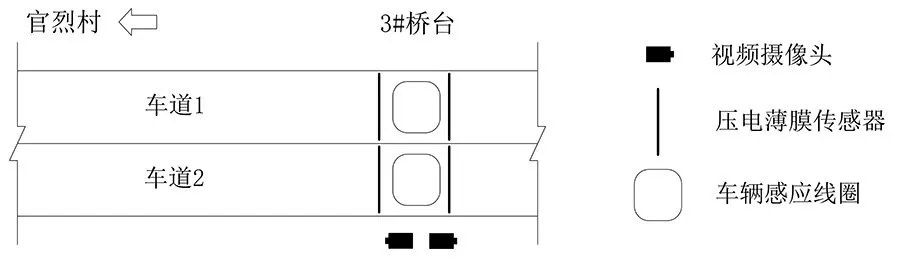
图2 桥梁实景图及WIM系统安装示意图

1 基于WIM数据的荷载特性统计与建模

本研究采集了该公路桥梁2019年11月至2021年2月的双车道WIM数据，共1 484 993辆车，对该区域的车辆数据进行车型组成、交通流量、车速、车重、轴重及车道分布差异的统计分析，并建立相关数学模型。

1.1 车型组成

通过对采集数据的分析，发现经过该桥的车辆主要由表1所示的5种车型组成。其中，轴距3 m的二轴车辆占62.15%，主要是轻型轿车；四轴货车占30.51%，是占比最高的货车车型，主要是周边采石场和采砂场的整体装卸式货车；三轴货车占6.79%，也是用于采石和采砂的整体装卸式车辆；剩余的五轴和六轴拖挂车占比不超过0.6%，表明该类拖挂车在本桥址不常见。上述货车组成表明四轴整体式装卸车是本桥最具典型的车型。

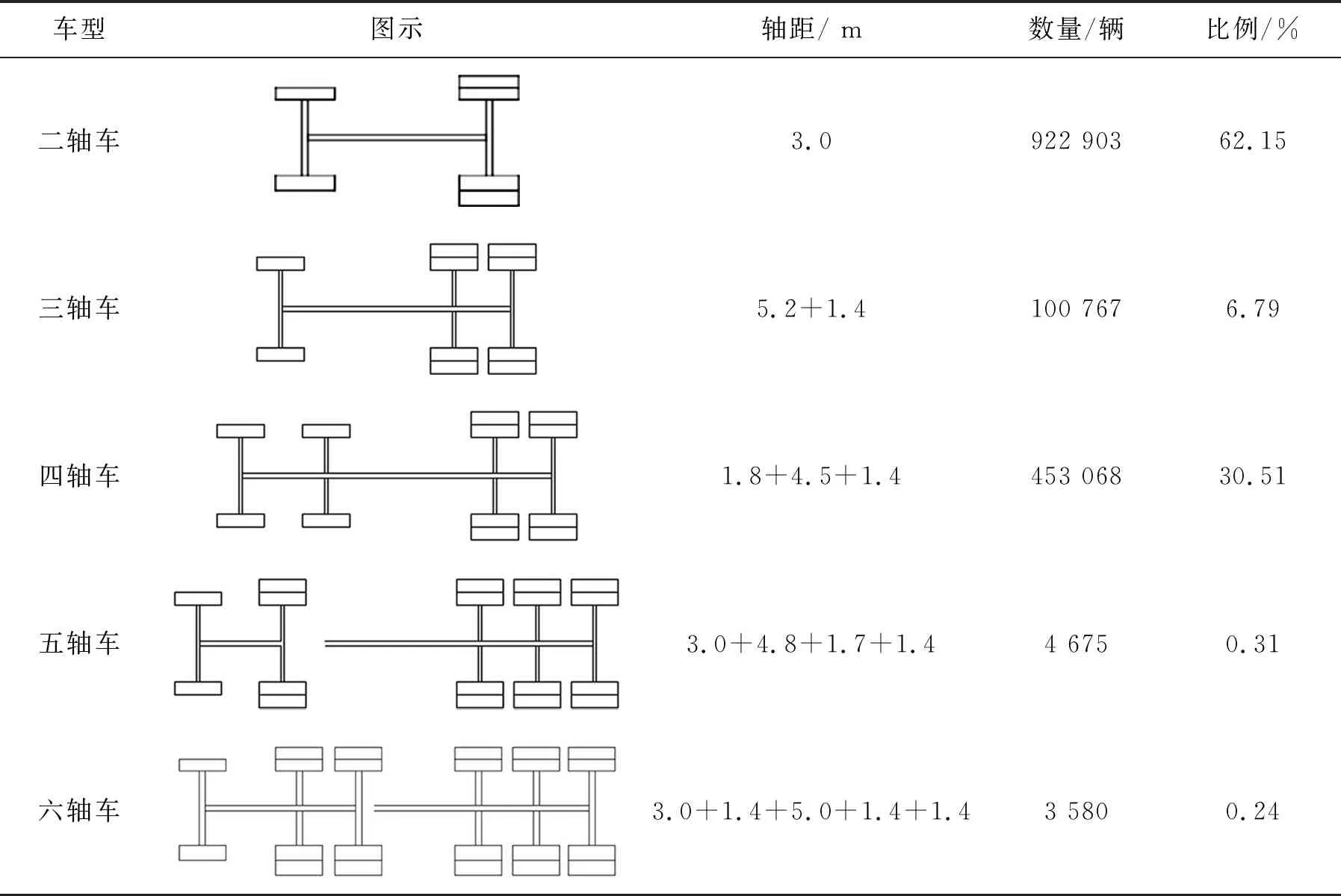
表1 基于WIM数据的车型组成分析

1.2 交通流量

统计16个月交通流量随时间的变化规律，如图3所示，除了春节假期交通量较少外，其余月份的交通流量基本呈现相同的规律。最大月交通流量为128 741辆/月，出现在9月份；最小月交通流量为23 482辆/月，出现在2月份,为春节假期。交通流量在常规月份规律基本相同，因此在后续分析中假定常规月份的车流量具有相同规律。

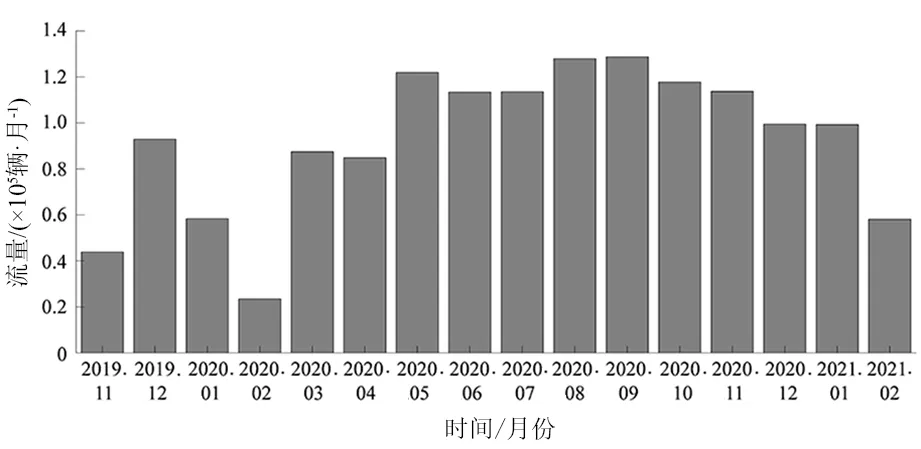
图3 月交通流量的时变规律

1.3 车速特性及建模

对不同车型的行车速度进行统计分析，结果如表2所示，车速基本服从正态分布，拟合误差RMSE基本在0.03以内与二级公路限速70 km/h一致。随着轴数的增加，车辆机动性能降低，其平均速度也逐渐降低。

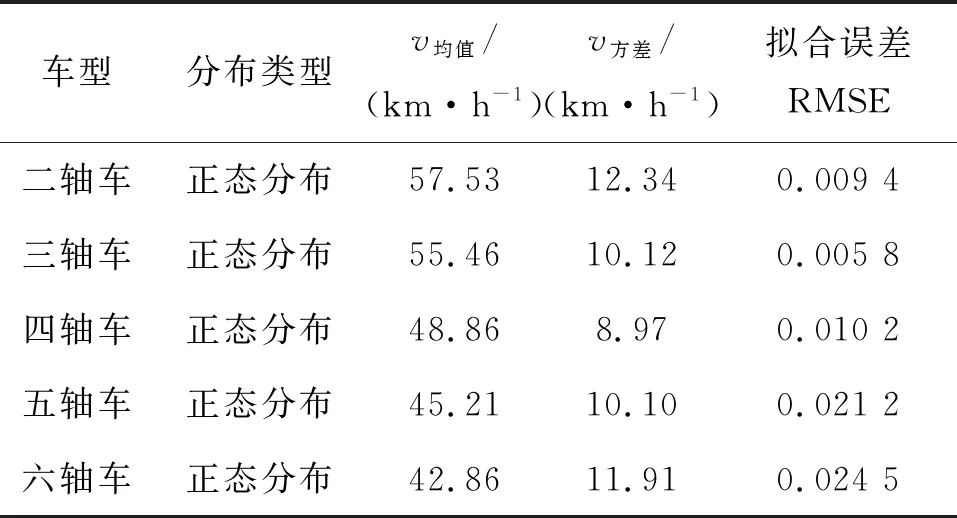
表2 基于WIM数据的车速统计模型特征

1.4 车重特性及建模

统计不同车型的车重分布，如表3所示，其中车重分布采用多峰正态分布进行拟合具有很好的拟合精度，拟合误差RMSE均在0.05范围内。从表3可以看到二轴车最大载重达到了39.46 t，已经严重超载，并呈现显著的重尾分布；三轴车总体呈现重尾分布特性，最大载重达到68.57 t但是平均载重为14.12 t；四轴车呈现双峰正态分布特性，最大载重83.41 t，平均载重33.24 t，超载率达到45.88%；五轴车也呈现双峰正态分布且最大载重达到90.56 t，超载率达到43.79%；六轴车呈现双峰分布特性，最大载重为109.66 t，超载率达到20.36%，上述车重特性表明车辆已经出现明显的超载特性。

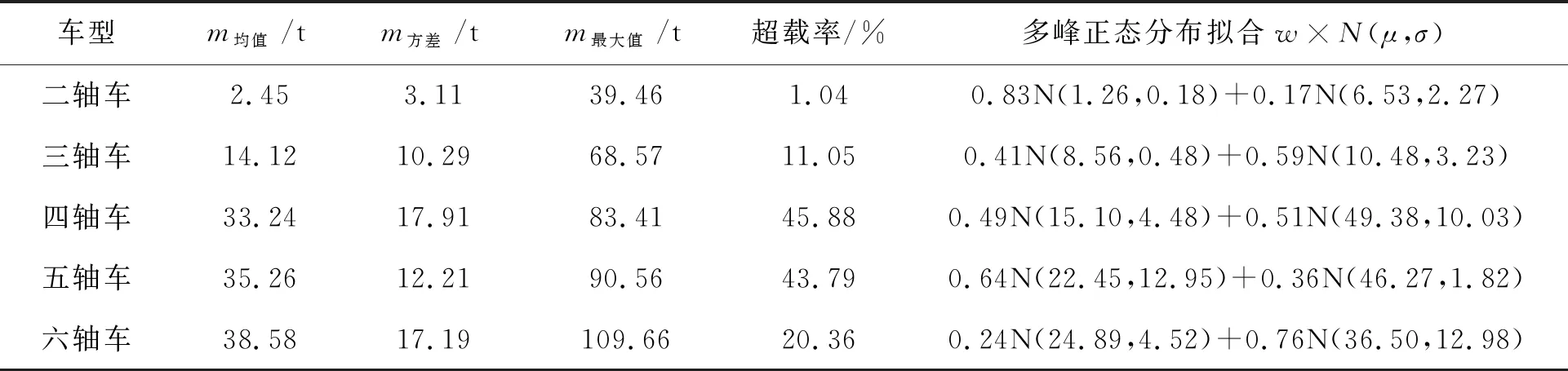
表3 基于WIM数据的车重统计模型特征

1.5 轴重特性及建模

对不同车型的轴重与车重关系建模，统计得到的相关性参数如表4所示，其中四轴车的统计关系如图4所示。本质上轴重和车重之间不是完全的线性关系，具有一定的随机性，但是遵循一个总体的线性关系，各种轴型车辆的轴重与车重关系可以通过表4的线性相关性系数进行描述。

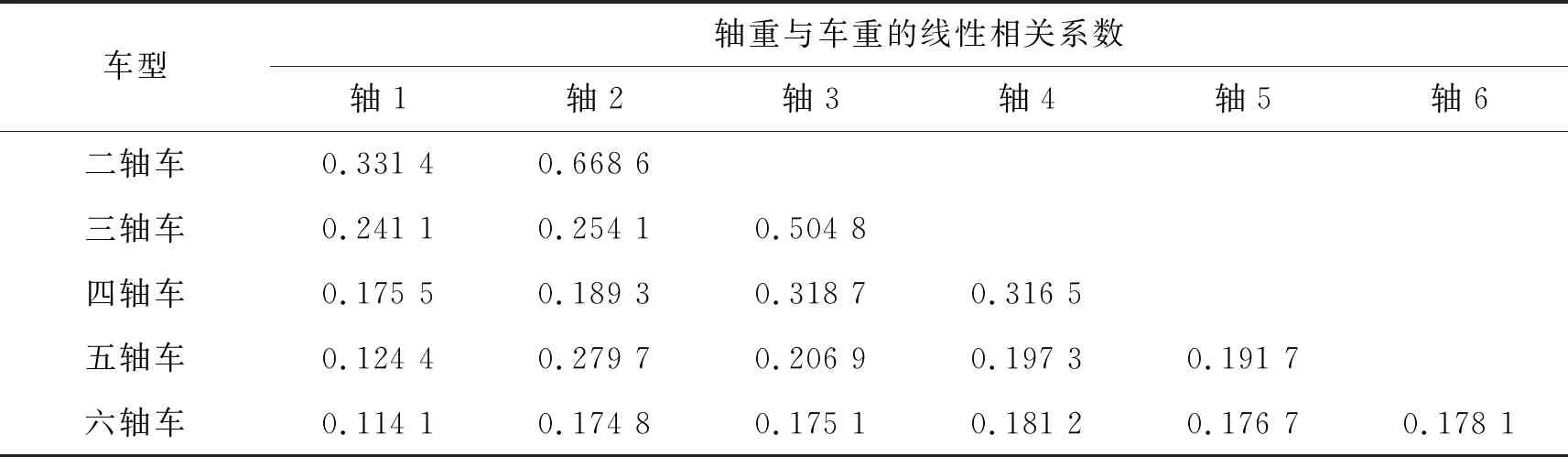
表4 轴重与车重的线性相关系数

1.6 车道分布差异性

在本研究中，桥梁为双向通行交通。经统计，车行方向1的总交通量为738 931辆车，车行方向2的总交通量为746 062辆车。

两个车行方向上的车辆车重累积概率分布如图5所示，可以看到两个行车方向上车重荷载具有显著的差别。表5给出了两个车行方向上车重统计分位值的对比，车行方向2的荷载显著大于车行方向1，主要原因是车行方向2是装载砂石出去的方向，而车行方向1是空车进入采石场方向。

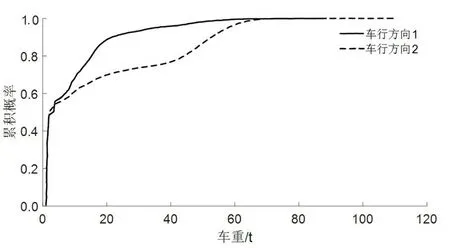
图5 不同车行方向车重分布累积概率直方图

表5 不同车行方向车重统计分位值对比

2 基于WIM的桥梁动力效应评估

WIM系统采集的是桥头断面车流荷载数据，这些车流过桥过程中会产生动力荷载效应。因此，将WIM采集数据接入随机车流-桥梁耦合动力模拟系统MSCA中，分析实际车队作用下桥梁动力挠度效应。选择28 m标准跨简支梁桥结构，不考虑桥梁损伤的情况下计算得到跨中位置各个梁肋的动力挠度响应时程。关于随机车流-桥梁耦合动力模拟系统MSCA请参阅文献[8]，MSCA经过验证可以重现实际采集数据在桥梁结构上的加载作用，对车流荷载效应分析具有较高的精度[9]，且能够用于各类复杂交通环境下的随机车流与桥梁耦合动力分析[8]。

图6是捕捉到的某时刻某车辆动态过桥过程中跨中各个梁肋的动态位移响应，可以看到是一辆货车过桥引桥的结构挠度变化，货车过完桥后桥梁仍然有小幅度的自由振动衰减。其中1#梁的最大位移为9.82 mm，2#梁最大位移为6.11 mm，3#梁最大位移为2.94 mm，而4#梁出现上挠现象最大位移为0.08 mm。引起上述位移变化特性主要是因为货车作用在靠近1#梁的位置，根据1#梁的动力位移响应，获取其动态挠度增量，计算得到的1#结构冲击系数为0.150 8，2#梁冲击系数为0.150 1，3#梁冲击系数为0.146 6，4#梁因为位移太小其计算冲击系数不具有参考意义。根据有限元模型计算获得该结构的基频为3.776 Hz，依照规范计算得到的冲击系数为0.22，显然规范计算结果要大于实测结果，说明规范对于冲击系数的考虑是较为安全的。由于采集的WIM数据跨越16个月，开展随机车流与桥梁耦合动力分析需要耗费较高计算时长，因此后续为了方便分析，采用0.22的计算冲击系数替代车桥耦合动力分析结果，且仅考虑随机车流的静力加载效应。

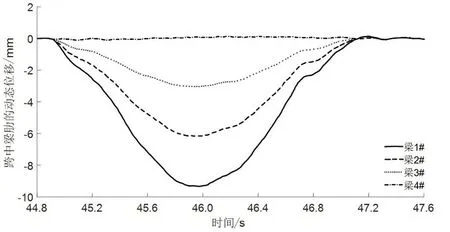
图6 某时刻某车辆动态过桥过程中跨中各个梁肋的动态位移响应

3 基于WIM的桥梁荷载效应分析

计算得到在16个月WIM数据作用下的各个梁肋的跨中弯矩和支点剪力，选取日最大值样本并绘制其累计概率分布如图7所示。在4个T梁的跨中弯矩和支点剪力相对关系中，1#梁的弯矩和剪力在整体上最大，而3#梁最小，与设计经验所认知的边梁荷载效应最大是相同的，因为运营荷载主要作用在最不利边缘位置，边间梁肋的荷载效应最为显著。

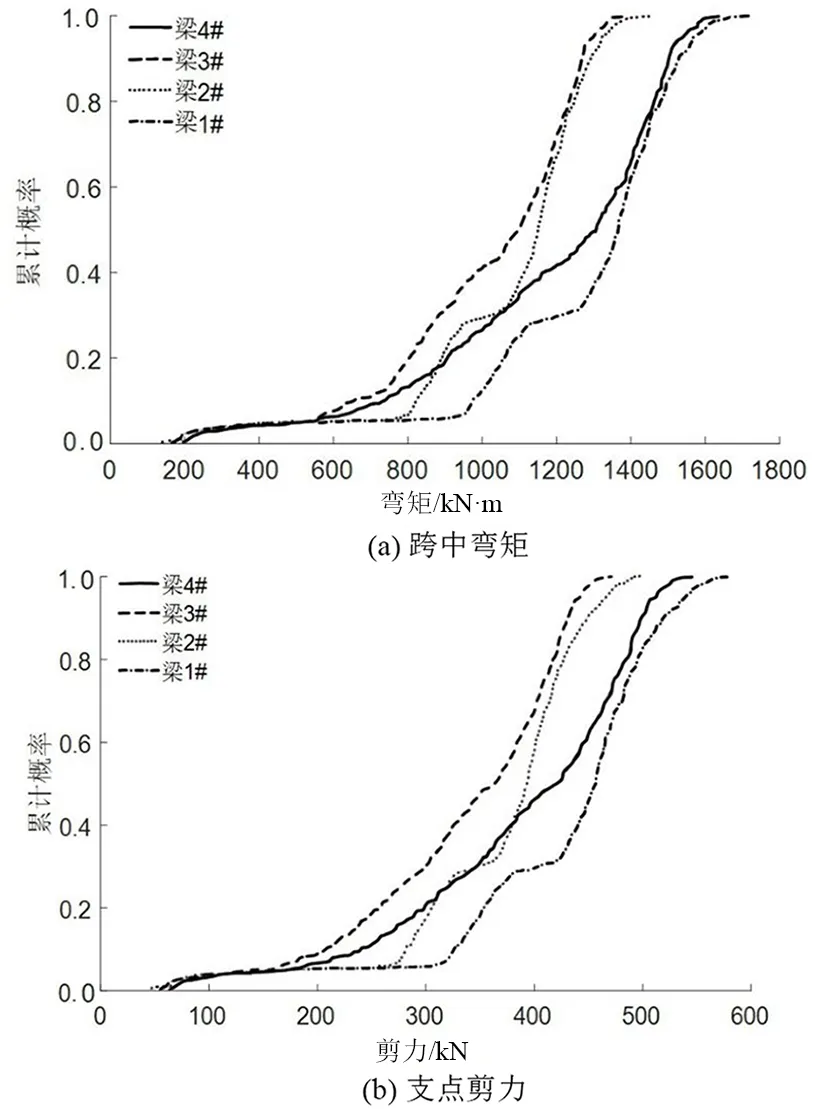
图7 各个梁肋日最大值荷载效应累计概率分布图

分析各个梁肋荷载效应的统计参数如表6所示，无论从均值、分位值还是最大值，边梁荷载效应均大于中梁荷载效应，且1#边梁荷载效应最为显著。将这些梁肋在WIM数据加载作用下的荷载效应与规范计算结果进行对比，有相当部分计算结果超过了规范值，所有荷载效应最大值均超过规范计算值。在超越规范计算值的概率上，1#边梁最为显著，跨中弯矩达到38%而支点剪力达到94%。这些统计结果表明该桥在实际车流荷载作用下荷载效应显著超过了规范计算值。弯矩荷载效应是规范计算结果的1.00～1.38倍，剪力荷载效应是规范计算结果的1.71～1.94倍。超过规范计算的荷载效应预示该桥梁结构具有显著的安全风险，需要进一步考虑荷载变异性及结构垮塌风险分析。

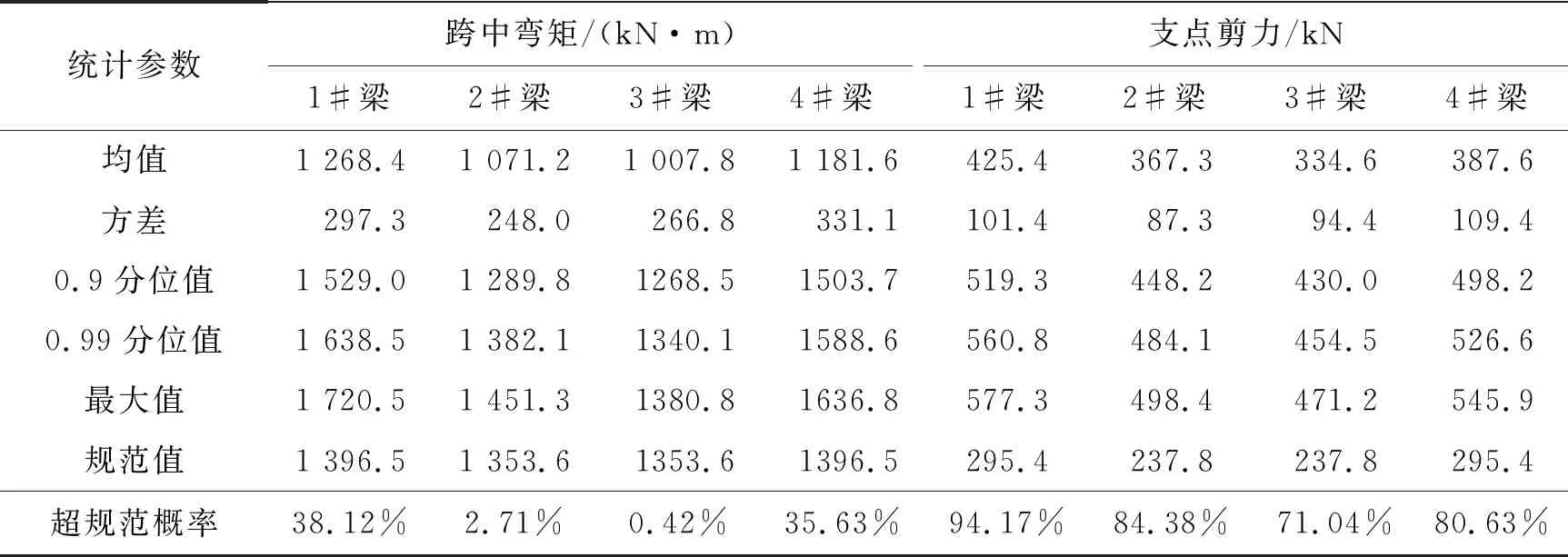
表6 各个梁肋荷载效应统计结果及其与规范计算值的对比

4 结论

1)桥址以四轴货车为主要交通主体、占有率达到30.51%，但是运输荷载最为显著的是六轴挂车，最大载重达到109.6 t；所有货车均有不同程度的超载，四轴货车超载率达到45.88%，显示出该桥址区域显著的超载重载现象；

2)通过随机车流与桥梁耦合动力分析发现，重载货车通行作用下桥梁的动力冲击系数为0.15，低于规范推荐的计算结果，表明规范对于本桥动力响应偏安全估计；

3)实际车流作用下各个梁肋的跨中弯矩和支点剪力存在一定程度的差异性，其中边梁荷载效应要显著大于中梁；车流作用下梁肋跨中弯矩是规范计算值的1.00～1.38倍，支点剪力是规范计算值的1.71～1.94倍，需要特别关注。