某电动汽车动力总成悬置系统优化设计

雷超宏，颜伏伍，吴 勇，王 武，李小荣，申秀敏

（重庆金康赛力斯新能源汽车设计院有限公司,重庆 401135）

无论是传统燃油汽车还是电动汽车，其动力总成的振动都会对整车的NVH 性能产生重要影响。合理的动力总成悬置系统设计能够提升隔振性能，有效地降低动力总成传递至车身的振动以及车内的噪声。为了提高悬置系统的隔振性能，需要对其进行解耦设计，尽可能地实现动力总成悬置系统多自由度的振动解耦。目前，常采用基于动力总成质心坐标系的六自由度动力学模型结合能量解耦方法对动力总成悬置系统进行解耦分析，并运用基于刚度系数的多目标优化、预定频率解耦、fgoalattain等方法进行解耦优化[1−3]，为悬置系统的设计提供了一定的参考依据。但是，由于未考虑车身系统、车辆的行驶工况等因素，仅依据六自由度悬置系统的解耦程度来预估或评判悬置系统在整车上的隔振性能是片面的。随着平台化、通用化、智能化等技术在汽车研发设计中的应用，许多车型在研发设计阶段已基本实现动力总成悬置系统与车身系统的同步开发，因此可在设计阶段对整车中的悬置系统进行更加深入和全面的研究分析。

本文以某电动汽车电机动力总成悬置系统为研究对象，运用扭矩轴理论和遗传优化算法对六自由度悬置系统进行解耦优化，并通过建立整车模型，在整车上分析和验证悬置系统的解耦特性和隔振性能，为悬置系统的开发设计提供了更全面的参考和指导。

1 基本理论

1.1 电机动力总成质心坐标系

对于传统的发动机动力总成，其坐标系统已有明确的定义[4−5]。鉴于电机动力总成结构不同于发动机动力总成，因而有必要重新定义电机动力总成的质心坐标系。图1 为某电动汽车的动力总成，主要由驱动电机、变速器、差速器及电机控制器等组成。图中G为电机动力总成质心位置，AA′为电机转子轴线，BB′为差速器扭矩输出轴线，且有AA′平行于BB′。将电机动力总成质心坐标系原点取在该动力总成质心G处，x轴平行于AA′且将变速器指向电机的方向定为x轴正向，z轴垂直于AA′和BB′所在平面且方向向上，y轴由右手定则确定。

图1 电机动力总成及质心坐标系

1.2 悬置系统固有特性及能量解耦

根据发动机动力总成悬置系统的建模方法[6]，将电机动力总成悬置系统简化为一个由刚体、弹簧和刚性地面组成的无阻尼多自由度振动系统。该系统的一般振动微分方程和自由振动微分方程分别为：

式中：[M]为广义质量矩阵；[K]为广义刚度矩阵；X为广义坐标；F为系统所受外部激励。

对式(2)求取特征值和特征向量便可得到动力总悬置系统的固有模态频率和振型，即：

式中：ω为系统的固有圆频率；ϕ为系统的振型。

从动力总成悬置系统的振型ϕ可以看出，通常悬置系统在6 个自由度方向上的振动是相互耦合的，当系统作各阶主振动时，系统的振动能量会分布于6 个自由度方向上，每一个方向上的振动能量占总的振动能量的百分比即为系统在该方向上的能量解耦率。当系统作i阶主振动时，第k个广义坐标上的能量分布矩阵[7]为

式中：Tpik为悬置系统在k个广义坐标上的解耦率；ϕi为悬置系统第i阶主振型；(ϕi)l和(ϕi)k为振 型ϕi的元素；mkl为质量矩阵M的元素。

Tpik值越大，悬置系统的解耦程度越高，当Tpik=100%时，表明系统实现了完全解耦。然而，在实际的工程应用中，要实现悬置系统完全解耦是十分困难的，只能尽量提高解耦率以达到一定的目标要求。

1.3 动力总成扭矩轴

由扭矩轴（torque roll axis，TRA）的定义[8−9]可知，在布置悬置时如若把悬置系统的左右悬置布置在扭矩轴上，动力总成只绕扭矩轴轴线振动，而不会引起绕其他轴线的转动和平动，此时悬置系统的隔振效果最佳。通过将式(1)进行处理便得到动力总成关于扭矩轴的响应。

式中，FTRA=[0,0,0,1,0,0]T，表示动力总成在扭矩轴方向上受到单位扭矩激励作用。

将动力总成的质量和惯性参数代入式（6）并化简，有：

根据上式求得动力总成绕各轴的转动分量及转动矢量方向，该矢量方向即为扭矩轴方向。结合动力总成质心位置，便可求出动力总成的扭矩轴线。

1.4 遗传算法

遗传算法是一种模拟生物进化过程的全局寻优算法，其核心内容包括参数编码、初始群体初始化、设计适应度函数、遗传操作（选择、交叉和变异）和控制参数等。由于遗传算法具有运算简单高效、鲁棒性强等特点，在工程上得到了广泛的应用[10−11]。

1.4.1 优化数学模型

1）适应度函数/目标函数。

运用能量法对动力总成悬置系统六自由度进行解耦是一个多目标优化，如若直接进行多目标优化会使问题复杂化，增加求解难度。因此，利用加权系数法将该多目标最大寻优问题转换为带有约束的单目标最小寻优问题[12]，即：

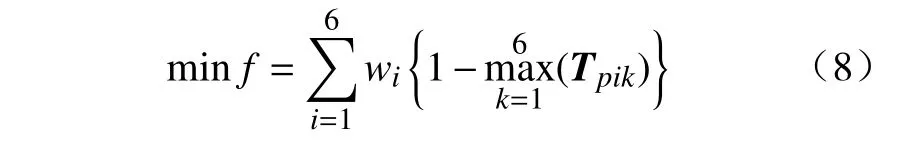
式中，wi为第i阶能量的加权因子。

2）设计变量。

动力总成悬置系统的动力学特性与动力总成和悬置系统的参数息息相关。由于动力总成的质量、转动惯量等参数很难改变，因而在进行悬置系统解耦优化时，通常考虑对悬置参数进行优化设计，如悬置安装位置、安装角度及各向刚度等。本文选取3 个悬置点的三向刚度作为设计变量，共计9 个变量参数。

3）约束条件。

①频率约束。由于该车辆的动力总成和后悬挂（通过仿真计算得到后悬挂两侧同向跳动频率10.8Hz，反向跳动频率11.6Hz）均安装于副车架上，为了满足二者的避频设计及避免悬置系统自身频率耦合，要求动力总成悬置系统的固有频率不小于13Hz 且频率间隔相差2Hz 以上。

②刚度约束。根据悬置设计经验，对于橡胶悬置的三向刚度进行取整优化，其非主要方向的刚度范围为100～200N/mm，其余两个方向的刚度范围为300～650N/mm，并且这两个方向的刚度比值为0.8～1.5。

③位移约束。为了避免运动干涉，动力总成在振动时各方向的位移量不超过10mm，悬置元件在振动时各向变形量小于5mm。

④解耦约束。在动力总成质心坐标系的x、y、z及绕x、y、z转动的θx、θy、θz共6 个自由度方向上，z向和θx向是电机动力总成悬置系统的主要激励方向，其解耦率要求达到90%以上，其他方向的解耦率达到80%以上，此时由动力总成引起的振动风险较低且能够处于可控状态。

1.4.2 遗传算法优化

确定设计变量、构建目标函数和约束函数后，在Matlab 优化工具箱中调用遗传算法函数ga 进行优化求解。由于该优化问题涉及大量的约束条件，包括悬置刚度整数约束、频率和解耦率等非线性约束，故需对ga 函数选择适用于这些约束条件的参数设置。表1 为遗传算法的相关参数设置，从编码方式至交叉概率等参数为ga 函数的默认参数设置，它们能很好地满足各种约束条件。同时，综合考虑优化求解的精度、稳定性及收敛性，将种群大小设置为100，将进化代数设置为300。

表1 遗传算法参数

2 实例分析

2.1 动力总成悬置系统参数

图2 为某电动汽车的动力总成悬置系统，其采用前2 后1 的3 点悬置布置形式。表2 为动力总成参数信息，其中质心位置和惯性参数的参照系分别为整车坐标系和动力总成质心坐标系。表3 为各悬置的弹性中心和三向刚度，它们的参照系分别为整车坐标系和悬置坐标系。由于3 个悬置的坐标系与整车坐标系方向一致，因而各悬置的三向刚度可看作整车坐标系下的刚度。

图2 动力总成悬置系统

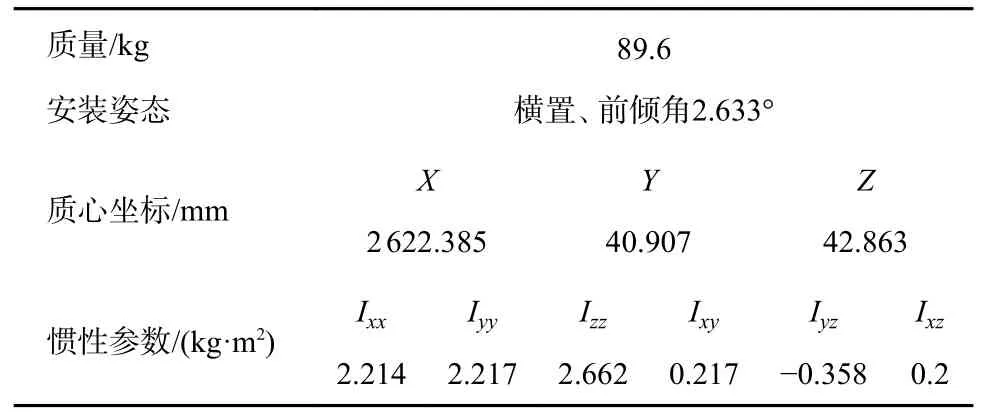
表2 动力总成参数

表3 悬置弹性中心和刚度

2.2 动力总成悬置系统解耦分析

基于六自由度刚体动力学模型及能量解耦法，对电机动力总成悬置系统进行解耦计算，得到悬置系统在动力总成质心坐标系下的解耦率如表4 所示。同时，根据扭矩轴计算方法得到该动力总成的扭矩轴，其在整车坐标系X、Y、Z方向的方向角分别为95.1604°、6.1722°和86.6229°。扭矩轴与各悬置的空间位置关系如图3 所示。

从表4 可以看出：悬置系统的z向和θx向的频率间隔只有1Hz，频率分布较近；在3 个旋转自由度方向的解耦率较低，其中在θx方向为扭矩激励方向，其解耦率只有80.48%，低于目标要求，同时在θy和θz两个转动自由度间存在较为严重的振动耦合，对悬置系统隔振十分不利。从图3 可以看出，右悬置靠近TRA 轴和质心位置，且位于质心下方较远，不利于动力总成的动态稳定性。因此，有必要对当前的动力总成悬置系统进行优化。

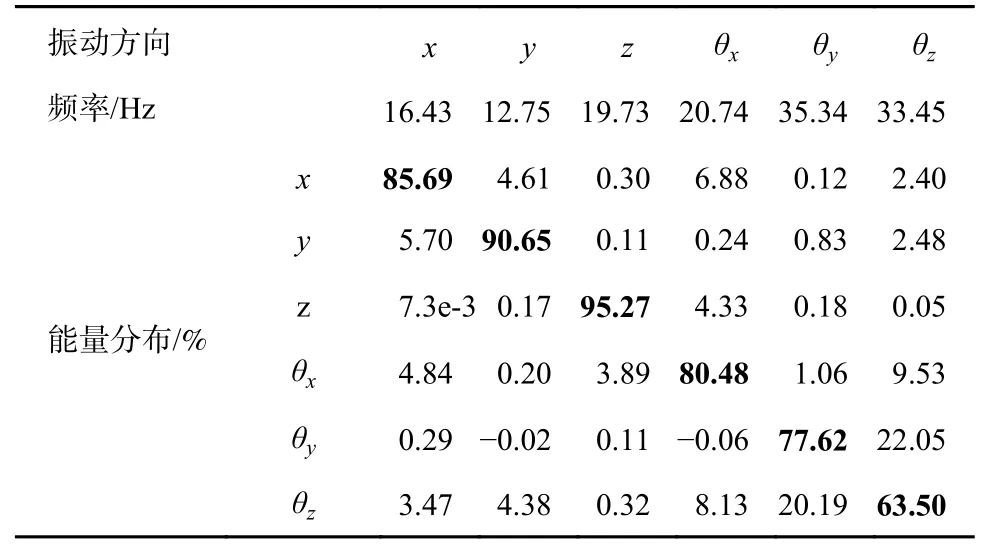
表4 动力总成悬置系统解耦率

图3 动力总成扭矩轴与各悬置的空间位置关系

2.3 悬置系统优化

2.3.1 扭矩轴优化悬置位置

基于该悬置系统的布置形式，参考燃油车的TRA 轴布置思路并结合工程应用，可将该悬置系统布置为：左右悬置连线尽量平行于TRA 轴，同时各悬置弹性中心应尽可能远离TRA 轴，从而使悬置受力最小和动力总成姿态变化最小[13]。最后，结合车身结构及整车总布置要求，左悬置和后悬置的位置保持不变，右悬置的位置调整至图4 所示，调整后动力总成TRA 轴及各悬置的空间位置关系如图5 所示。

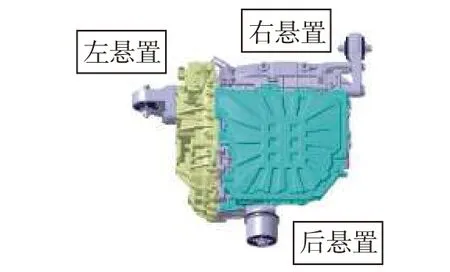
图4 调整后的右悬置

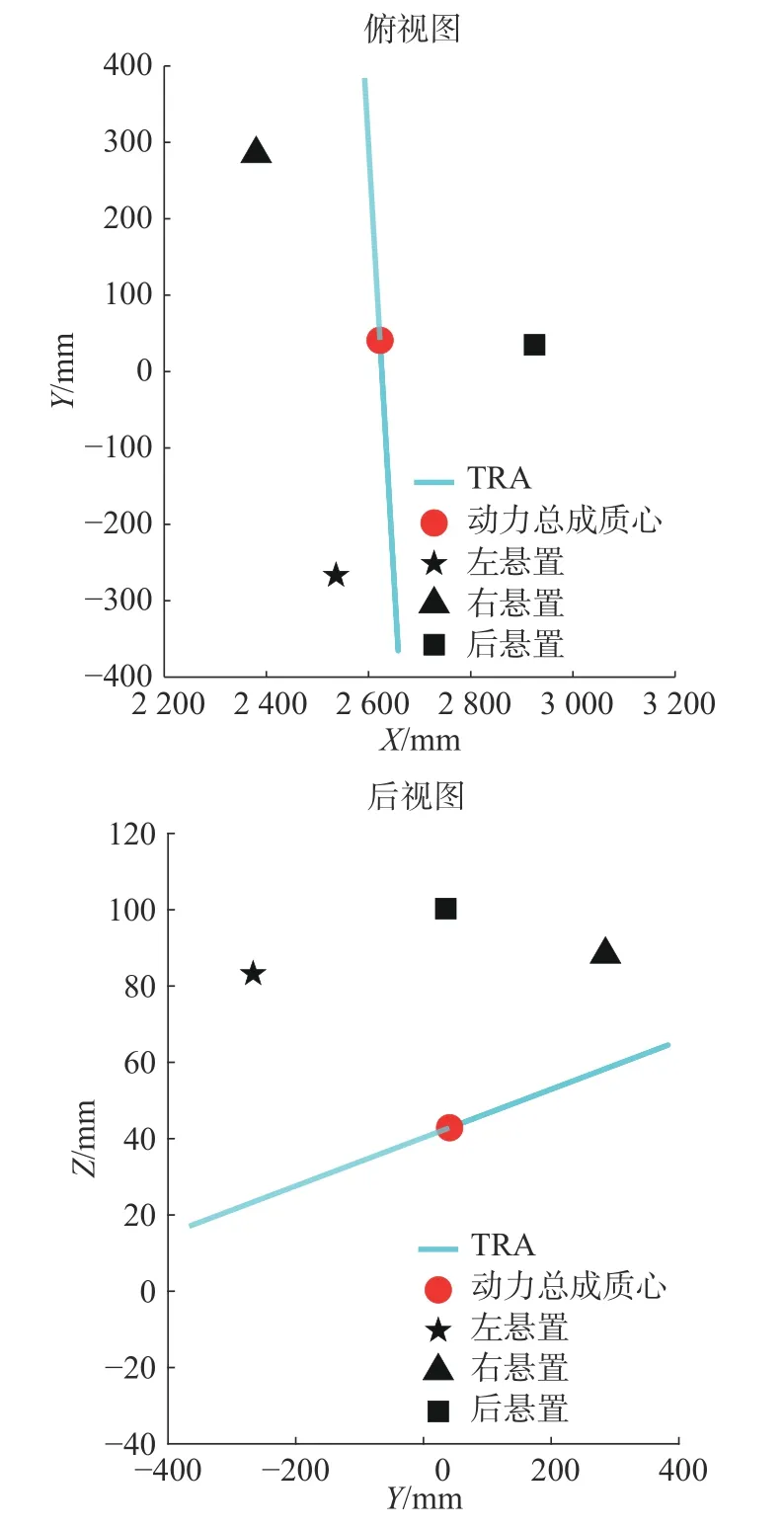
图5 右悬置调整后动力总成扭矩轴与各悬置的空间位置关系

从图5 可以看出，右悬置位置调整后左右悬置连线与TRA 轴的平行度较原状态更好，动力总成质心位于悬置下方且更靠近3 个悬置的几何中心，使得各悬置受载更加均衡且动力总成的动态稳定性更好。

2.3.2 遗传算法优化悬置解耦

根据上述遗传算法优化思想对各悬置的刚度进行优化设计，得到动力总成悬置系统各悬置点的刚度及对应的悬置系统解耦能量分布分别如表5和表6 所示。

表5 优化后悬置弹性中心和刚度

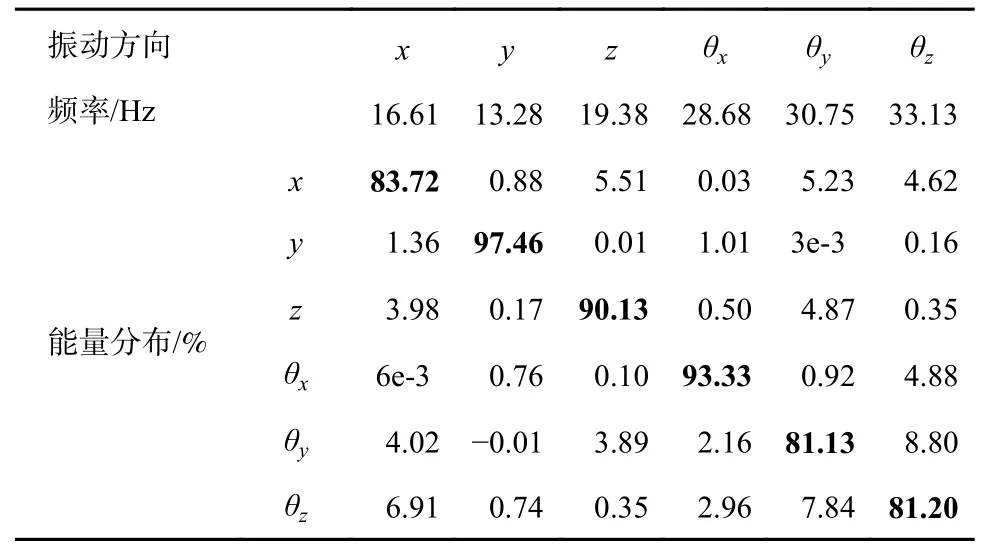
表6 优化后悬置系统解耦率

对比表4 和表6 可知，位置和刚度优化后，无论是频率分布还是解耦率均满足约束条件要求。对于解耦率而言，悬置系统在3 个平动自由度方向的解耦率有升有降，3 个转动自由度方向的解耦率得到明显提升。

3 仿真验证分析

3.1 整车状态解耦分析

动力总成悬置系统作为一个振动子系统安装于车身上，其解耦特性将会受到车身刚度、动力总成安装姿态以及参考坐标系等因素的影响。为了尽可能地反映出动力总成悬置系统的真实解耦情况，在整车状态下对悬置系统进行解耦特性分析是十分必要的。

首先，采用有限元方法搭建整车状态下的动力总成悬置系统动力学模型（见图6），而后求解整车状态下的动力总成的模态特性，最后结合能量解耦的方法对整车状态的动力总成悬置系统进行解耦计算。表7 和表8 分别为解耦优化前后悬置系统在整车状态下的解耦情况。

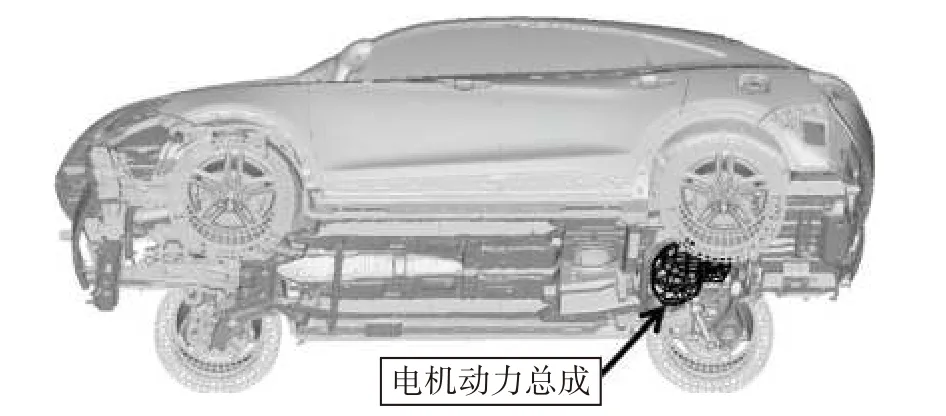
图6 整车有限元模型

表7 优化前整车状态悬置系统解耦率

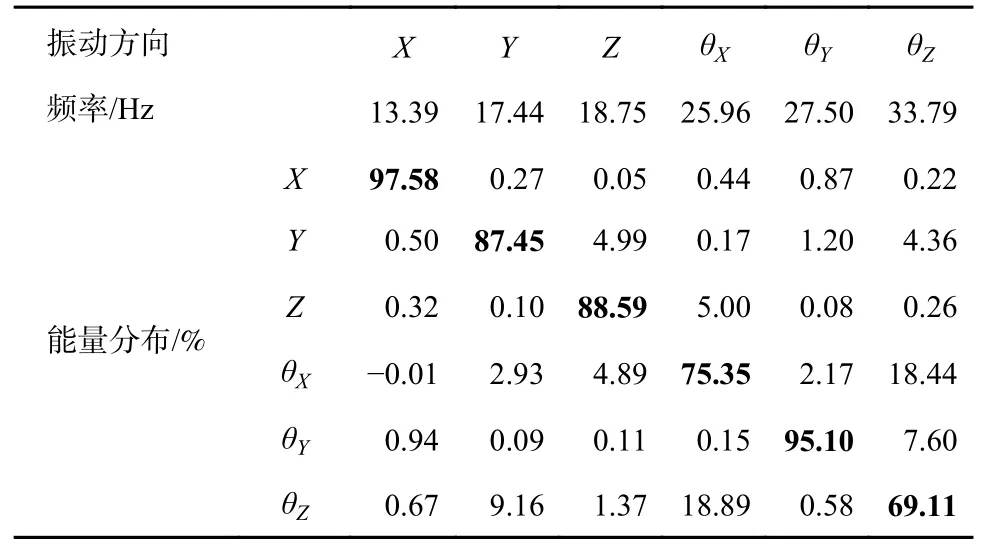
表8 优化后整车状态悬置系统解耦率

从表7 和表8 可以看出：优化后整车状态动力总成悬置系统的固有频率范围为13.39～33.79Hz，频带变窄，且最小频率间隔为1.31Hz，频率分布较为合理；优化后悬置系统除了Z向平动自由度的解耦率与优化前相当，其他5 个自由度方向的解耦率均有明显提升。尽管如此，优化后悬置系统在整车的θX、θZ向的解耦率只有75.35%和69.11%，解耦率较低，但考虑到这两个方向不是主要激励方向，引起NVH 问题的风险较低。

3.2 瞬态特性分析

动力总成悬置系统解耦优化的最终目的是提升悬置系统的隔振性能，减小振动向车身传递，因此可通过分析动力总成自身及其与车身之间的振动传递直接反映出悬置系统的性能。

电机具有输出扭矩大且响应迅速的动力特性，使得电动汽车比传统燃油车具有更好的动力性能和加速性能。但当电机输出扭矩突变时容易引起动力总成振动增大，进而引起车身振动变大或者异常抖动问题，此时，合理的悬置系统设计显得尤为重要。

为了验证解耦优化后的悬置系统在电机动力总成输出扭矩突变时的隔振性能，对车辆以最大驱动力矩原地起步加速行驶工况进行瞬态分析，该工况不仅可以评判车辆的动力性，还是评判车辆NVH 性能的典型工况之一。在该工况下，电机扭矩（不考虑扭矩波动）加载曲线如图7 所示。在0～0.5s 车辆处于静止状态，在0.5s 时电机开始输出扭矩并在0.04s 内增加到最大值310N·m 并保持最大输出扭矩行驶。针对车辆的这一行驶工况，利用Optistruct 软件对车辆进行瞬态特性仿真分析，得到动力总成和车身（方向盘和主驾地板）的瞬态振动响应。图8 为解耦优化前后动力总成在X、Y、Z方向的瞬态响应，图9 为车身振动瞬态响应，其中图9(a)和图9(b)分为方向盘、主驾地板在X、Y、Z方向上的瞬态振动响应。

图7 电机扭矩加载曲线

从图8 和图9 可以看出，在0.5～2.5s 的时间段为车辆的主要瞬态响应阶段，各方向的曲线振动较大，之后振动趋于平稳，进一步观察发现以下现象。

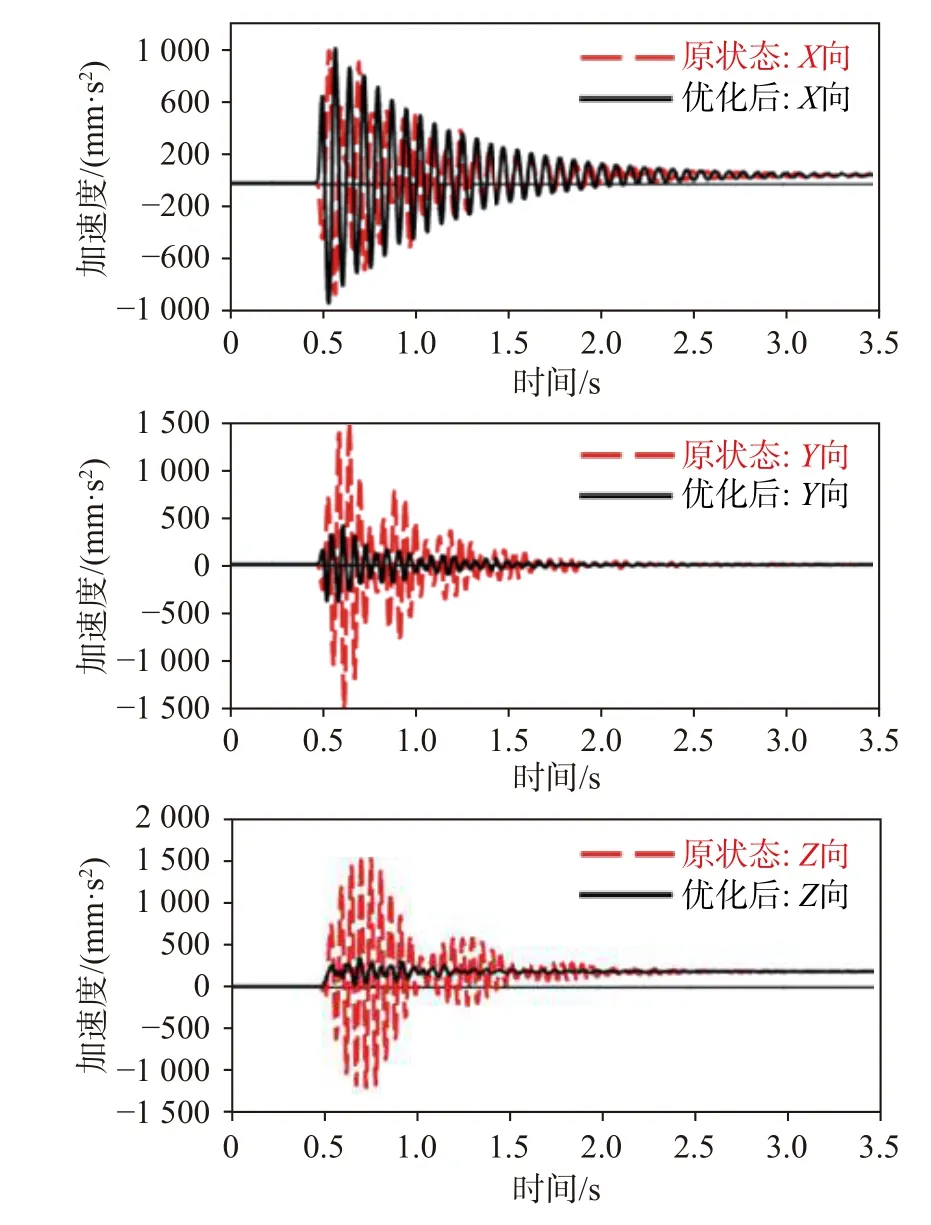
图8 电机动力总成瞬态振动响应

图9 方向盘和地板瞬态振动响应

1）解耦优化前，动力总成在整车Y向和Z向的瞬态振动衰减过程出现明显的“减小–增大–减小”衰减反复现象，从而导致方向盘和地板在相应方向上振动衰减也出现这一现象，这将严重影响车辆的NVH 性能。

2）解耦优化后，动力总成和车身的振动衰减反复现象消失。对于动力总成，其在X向的振动略微减小，在Y向和Z向的振动明显减小，其中Y向的最大振动由约1500mm/s2减小到400mm/s2，Z向的最大振动由约1600mm/s2减小到400mm/s2。对于车身上的方向盘和地板，其各个方向的振动均明显降低，尤其是Y向和Z向的振动降低十分明显。

综上可知，悬置系统解耦优化后电机动力总成的隔振性能得到了提高，车辆的瞬态响应特性得到了显著改善。

4 结论

1）通过解耦优化，六自由度悬置系统在主要激励方向θx的解耦率由80.48%提升到93.33%，在θy、θz方向的解耦率分别由77.62%、63.50%提升至81.13%、81.20%。同时，悬置系统在整车θX、θY、θZ向的解耦率分别由62.19%、85.96%、63.78%提升至75.35%、95.10%和69.11%，优化效果明显。

2）解耦优化后，车辆在原地起步加速工况下，动力总成在Y、Z方向的瞬态振动减小约75%。方向盘和地板在X、Y、Z向的瞬态振动明显减小，其中在Y、Z方向瞬态振动减小约50%，车辆的瞬态特性得到了改善。

因此，通过运用扭矩轴理论和遗传算法对电机动力总成悬置系统的悬置位置和刚度进行优化设计，有效地提升了该悬置系统的解耦特性和隔振性能，提高了车辆的乘坐舒适性。