浮尘天气条件下无线紫外光通信的传输特性
宋 鹏,马守领,张国青,郭 华,张利剑
(1.西安工程大学 电子信息学院,陕西 西安 710048;2.西安工程大学 理学院,陕西 西安 710048)
0 引 言
“日盲”波段(200~280 nm)紫外光具有背景噪声小,可实现非直视(non-line-of-sight, NLOS)传输等特点,逐渐成为近年来无线光通信领域研究的热点[1-2]。沙尘气溶胶对自由空间光通信的影响已成为目前研究的重要分支之一[3]。浮尘气溶胶是沙尘气溶胶的一种,其粒径≤10 μm,常以PM2.5和PM10含量评定浮尘天气等级[4-5]。浮尘粒子受重力、浮力等合力作用可以长时间悬浮于大气中,导致浮尘天气下的水平能见度小于10 km。因此,研究浮尘天气下紫外光通信信道特性,对紫外光通信系统性能的提升具有重要意义。
关于沙尘气溶胶,学者多是采用Mie散射理论和蒙特卡罗仿真方法进行研究。2010年,郝丽等在沙尘气溶胶复折射效率指数和对数分布的基础上,利用Mie散射理论对沙尘气溶胶的消光、散射和吸收效率因子与粒径的相互关系问题进行了仿真和分析,得出消光和吸收效率因子随粒径的变化而发生振荡和衰减,且随着波长的增大,其振荡特征逐渐消失[6],2013年,王红霞等应用蒙特卡罗方法,对激光在煤烟型、沙尘性、海洋性和水溶性等4种气溶胶粒子下的传输特性和通信性能进行了分析对比[7];2018年,杨玉峰等使用MC方法和Mie散射理论进行了仿真和对比,研究火星沙尘天气条件下激光传输衰减及透射率、能见度随粒子浓度变化的关系[8];2019年,CAO等采用辐射传播法和小角度近似法,从宏观上分析了激光在沙尘信道中的传输特性,得出沙尘天气下的自由空间光通信多重散射效应占据主导地位,且多重散射是导致信号延迟和脉冲展宽的主要原因等结论[9]。
目前,对沙尘天气下紫外光通信的研究大多集中于理论分析阶段,缺乏相应的实验验证。事实上,沙尘粒子的浓度和粒径的变化都会影响紫外光的通信性能。本文基于浮尘粒子的尺度谱和Mie散射理论,利用蒙特卡罗仿真方法,对不同浮尘天气下的紫外光通信性能进行了仿真分析,并对晴朗、严重浮尘和极度严重浮尘3种不同浮尘浓度对紫外光通信性能的影响进行了实验分析。
1 理论基础
1.1 浮尘气溶胶
大量的实验和研究表明,浮尘天气下气溶胶包含各种粒径大小的粒子,且其粒子的尺度谱N(r)可以由对数正态分布曲线较好的拟合[10-11],对数正态分布可以表示为
(1)
式中:N0为粒子数密度;r为粒子半径;r0为气溶胶粒子的几何平均半径;σ为粒子的几何标准偏差。
根据文献[11]给出的参数,浮尘天气下,r0和σ的取值分别为0.21和2.45。严重浮尘条件下粒子数浓度为1 400 个/cm3,极度严重浮尘条件下粒子数浓度为2 000个/cm3。根据式(1),可得严重浮尘和极度严重浮尘的粒子谱分布,如图1所示。

图 1 浮尘粒子谱分布Fig.1 Spectral distribution of floating dust particles
1.2 Mie散射理论
浮尘粒子粒径较小,但其直径远远超过了紫外光的波长,故可将其视为球形粒子,选用Mie散射理论研究其散射问题。
根据Mie散射理论,消光效率因子Qext、散射效率因子Qsca和吸收效率因子Qabs可表示为[12-13]
(2)
式中:an、bn为m和α的函数[14-15]。
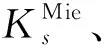
(3)
式中:Nv(r)是Mie粒子的浓度分布,可由式(1)求得;Qsca(r)和Qabs(r)可由式(2)求得。
由式(2)得出不同尺度参数α下浮尘粒子的Qext(r)、Qsca(r)和Qabs(r)值,如图2所示。

图 2 浮尘粒子的效率因子Fig.2 Efficiency factor of floating dust particles
由图2可以看出,浮尘粒子的Qext(r)和Qsca(r)曲线呈现振荡衰减趋势。随着尺度参数α的增大,Qext(r)最终振荡收敛于2.07附近,Qsca(r)最终振荡收敛于1.14附近。Qabs(r)曲线随着尺度参数的增大起初是呈现单调增加的趋势,当尺度参数α增加到100左右时曲线趋于平缓,最终曲线收敛于0.92附近。
1.3 非直视散射传输模型
紫外光非直视散射传输模型如图3所示。
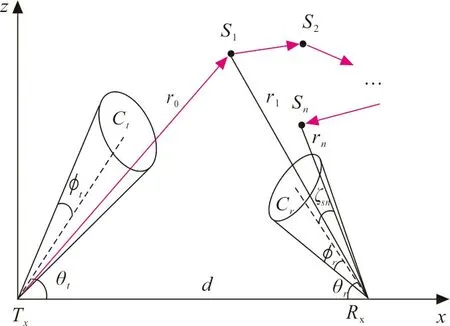
图 3 非直视散射传输模型Fig.3 NLOS scattering transmission model
图3中,d为发送端Tx与接收端Rx间的距离;θr和θt分别为Rx和Tx的仰角;S1,S2,…,Sn为n个散射点;φr为接收端半视场角;ζsn为Sn和Rx的连线与接收视场光锥中轴线的夹角。只有满足ζsn<φr,光子才有可能被接收[17]。
光子经粒子散射,在不同方位上辐射出光子概率的大小可由散射相函数描述。本文中,散射相函数由瑞利散射和米散射两者相函数的加权和表示[18-19],即
(4)
式中:θs为光子在散射点的入射方向与出射方向的夹角;PRay(cosθs)和PMie(cosθs)分为瑞利散射和Mie散射的相函数[19]。
光子经过Sn点散射后指向接收面的概率为
(5)
式中:A为接收端Rx的接收面积。
光子经过Sn点散射后,传输rn距离的概率为
P2n=exp(-Kern)
(6)

一个光子经过第n次散射后能够到达接收端的概率为[21-22]
Pn=WnP1nP2n
(7)
式中:Wn是光子能够到达散射点Sn且存活的概率,可表示为
Wn=Wn-1(1-Pn-1)exp(-Ka|Sn-Sn-1|)
(8)

N个光子经过散射后到达接收端的总概率为
(9)
从发射端到接收端系统总的路径损耗L为[23]
(10)
2 实验与仿真
2.1 仿真分析
对不同浮尘浓度条件下紫外光的通信性能进行仿真。浮尘粒子的复折射率取为m=1.53-0.008i,如不做特殊说明发送端仰角和接收端仰角变化角度相同。系统的仿真参数如表1所示,依据式(3)得到不同浓度条件下的散射系数和吸收系数,如表2所示。

表 1 仿真参数
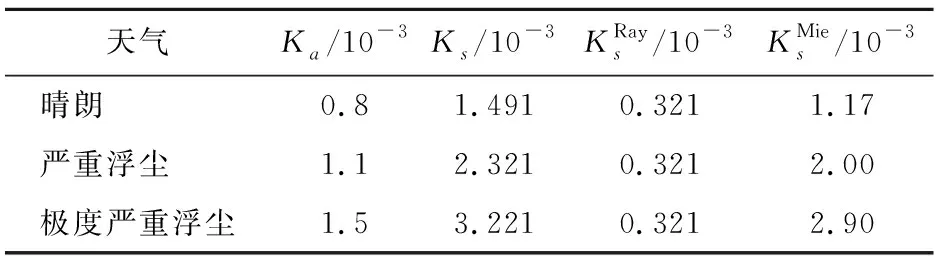
表 2 不同气象条件下的散射系数
为研究粒子谱分布下浮尘粒径对紫外光通信性能的影响,分别在严重浮尘和极度严重浮尘2种情况下,依据式(3)计算出的不同粒径下浮尘粒子的瑞利散射系数和吸收系数,对粒径为0.5~10 μm,步进为0.5 μm下的紫外光的通信性能进行仿真。收发端之间的通信距离为30 m,收发端仰角相同。严重浮尘与极度严重浮尘天气下不同粒子粒径与路径损耗的关系如图4所示。
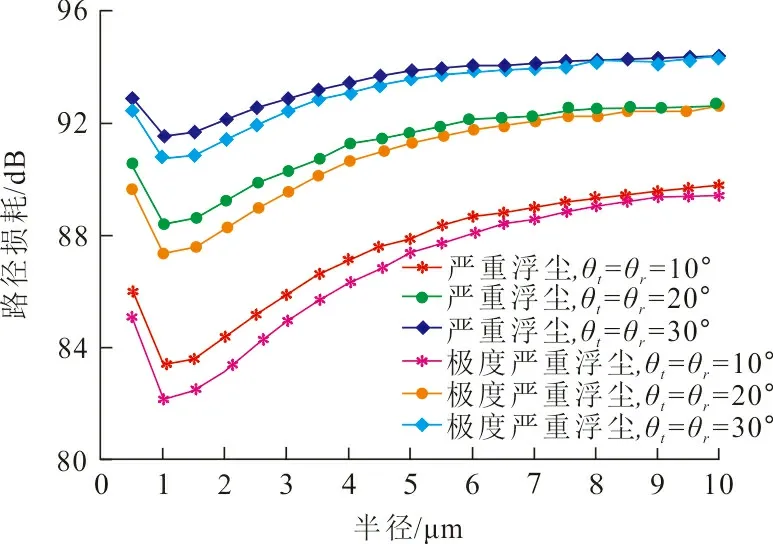
图 4 粒子半径与路径损耗的关系Fig.4 Relationship between particle radius and path loss
从图4可以看出:2种浮尘条件下,随着粒径的增大,无论收发仰角如何变化,仿真得出的路径损耗都呈现先减小后增大的趋势,出现最小值的粒子半径在1.0~1.5 μm之间。极度严重浮尘条件下的通信性能整体上要比严重浮尘条件下的通信性能好。从图4还可以看出:当收发仰角相同时,极度严重浮尘条件下的路径损耗要比严重浮尘条件下小1 dB左右;随着粒子半径增大,两者差值逐渐减小,半径为6 μm以后基本趋于一致。这是因为浮尘粒子半径较小,如图1所示,浮尘粒子大多集中于6 μm以下,且粒径越大空气中含量越少,对紫外光的散射作用也就越小。因此,随着粒径增大,严重浮尘与极度严重浮尘2天气情况下的通信性能趋于一致。
2.2 实验分析
2.2.1 实验条件
为了更好的研究实际浮尘天气紫外光通信性能,2021年春季在西安工程大学临潼校区19∶00~21∶00,分别在晴朗、严重浮尘、极度严重浮尘天气条件下测试紫外光通讯性能。实测时的天气参数如表3所示。

表 3 天气参数
紫外光室外实验所用通信设备如图5所示。在信号发送端采用型号UVTOP255TO39BL的紫外LED作为光源,中心波长为255 nm,全发散角为6°,发射功率Pt=0.3 mW;接收端采用型号滨松R7154侧窗型光电倍增管(PMT)作为信号接收器件,光电转换效率ηd=30%,不加滤光片。

(a) 发送端
2.2.2 实验路径损耗的计算
实验接收到的信号功率Pr[24]为
(11)
式中:E为单个光子能量;I=U/R,U为接收信号电压幅值;ηd为光电转换效率;ηf为滤光片透过率;G为光电倍增管增益;e为电子电荷量。
实验信号路径损耗的计算可表示为[25]
L=10lg(Pt/Pr)
(12)
2.3 结果对比与分析
严重浮尘天气下,使用图5所示装置,发送频率为10 kHz的方波信号,通信距离40 m,收发仰角θt=θr=10°,接收到的信号波形如图6所示。该通信条件下接收到的信号波形较为规整,可以对信号进行抽样判决。从接收波形可以看出:该通信条件下的背景噪声约为100 mV,信号有效电压约为0.9 V。将得到的信号有效电压代入式(11)、(12),即可得出此信号的路径损耗。
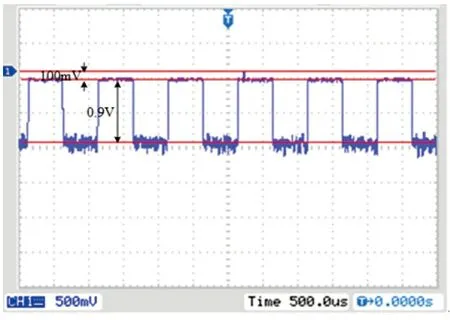
图 6 严重浮尘天气下接收的信号波形Fig.6 Signal waveforms received in severe floating dust weather
浮尘天气下紫外光的散射通信是在整个粒子谱共同作用下实现的,在对其进行仿真时要充分考虑整个粒子谱的散射作用。为研究不同收发仰角下浮尘天气对紫外光通信系统性能的影响,首先仿真分析了不同天气条件下收发端仰角为10°和20°的紫外光通信性能,之后进行实验对比。不同浮尘天气下路径损耗与通信距离之间关系的仿真与实验结果如图7所示,图7中通信距离10~80 m,步进为10 m。
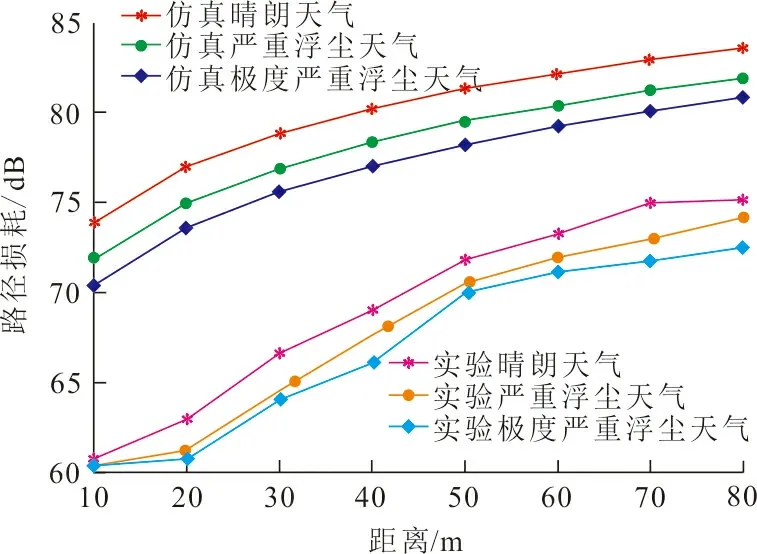
(a) θt=θr=10°
图7(a)固定收发仰角θt=θr=10°,图7(b)固定收发仰角θt=θr=20°。
对比图7(a)、(b)可以看出:固定收发仰角,紫外光通信系统的路径损耗随着通信距离的增加而增大。当通信距离固定时,随着收发仰角的增大路径损耗呈现递增趋势,但系统路径损耗随着浮尘浓度增大(浮尘天气严重)而减小。原因是随着浮尘浓度增加,在公共散射区域内可用于散射作用的粒子数增多,散射系数增大,紫外光子经粒子散射后到达接收端的概率增大,所以路径损耗会随着浮尘浓度增大而减小。由于光子到达接收端的概率与收发端仰角成反比关系,因此路径损耗随着收发仰角的增大而增大。
从图7还可以看出:虽然仿真和实验得到的路径损耗的趋势相同,但仿真结果都大于实验结果,通信距离越近这种现象越明显;距离越远且仰角越大,仿真结果与实验结果拟合越好。出现这个现象的原因是,在蒙特卡罗仿真程序中,当光子打到地面时,认为该光子变为“死光子”,也就是光子不再传输,而实验中确实有一部分光子经过地面反射后继续运动,并最终到达接收端,从而导致与仿真结果相比,实验得到的路径损耗偏小。相关实验可以验证这个解释:设定通信距离为30 m,收发仰角分别设定为-10°和-20°,接收到的信号波形如图8所示。
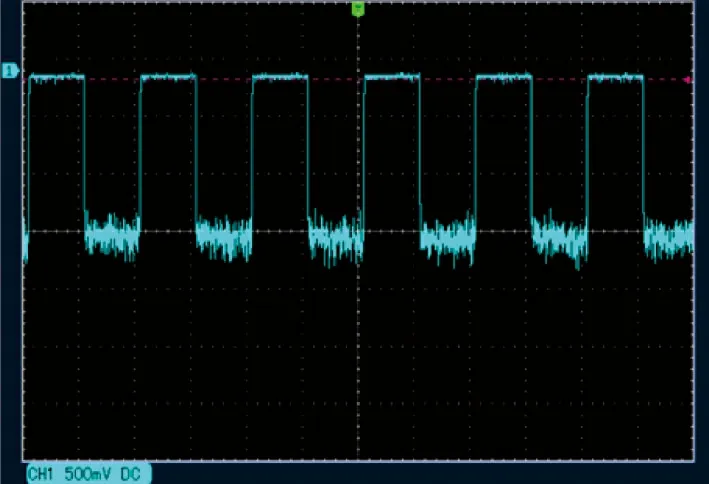
(a) θt=θr=-10°的信号接收波形
由图8可以看出:距离30 m处,收发仰角都为-10°时,接收到的信号电压约为1.4 V; 收发仰角都为-20°时,接收到的信号电压约为0.39 V。由此可以判定,实验中确实有光子经地面反射到接收端,并由此引起与仿真结果相比实验测试所得路径损耗偏小。
3 结 语
本文研究浮尘天气下紫外光通信性能:首先基于浮尘的粒子谱,采用Mie散射理论分析了浮尘粒子各粒径下的散射性能; 之后采用蒙特卡罗方法分析浮尘信道下的通信性能,并与不同天气条件下的实验结果相对比。结果表明:1)浮尘粒子的散射效率因子和消光效率因子呈现振荡衰减趋势,且随着尺度参数的增大最终分别振荡收敛于2.07和1.14附近。2)当浮尘浓度一定时,紫外光通信的路径损耗随粒径的增大呈先减小后增大的趋势,出现极小值的半径范围在1.0~1.5 μm之间。3)在浮尘天气下短距离通信时,紫外光通信的路径损耗随着浮尘浓度的增加而减小,随着通信距离和收发仰角的增加而增大。

