机器人示教缝纫动作的学习方法

王皞燚，王晓华，王文杰

(西安工程大学 电子信息学院，陕西 西安 710048)

0 引 言

随着机器人技术的发展，人们期望机器人具有更高级的技能[1]。协作机器人可以与工人良好合作，或者机器人真正替代人类完成工作任务[2-3]。

在学习人类技能的过程中，机器人需要依赖传感器获取作业环境以及作业工序中的操作信息[4-6]。在机器人技术发展的最初阶段，机器人通常仅依靠安装于末端的力传感器感受操作信息[7]，并采用一定的学习机制自适应地完成作业任务[8]。YIN等应用机械手上力传感器测量实际力的大小，并根据与模糊逻辑定义的织物期望张力之间的误差调整控制器参数，使得机械手能够完成类似场景的缝纫作业[9]。KOUSTOUMPARDIS等设计了基于神经网络的力控制器，机器人在缝纫过程中对织物施加期望的张力并完成运动动作。该缝纫机器人能够实现对不同织物的缝制[10]。YOUSEFIZADEH等运用力传感器将工人缝纫操作时手部产生的力传递到机器人末端执行器，并设计力阻抗控制器，实现人与机器人的协同缝纫控制[11]。随着传感器技术的发展，YOSHIMI等使用激光传感器检测缝纫部件边缘线，生成期望的缝纫轨迹，机械臂通过轨迹跟踪实现缝纫[12]。机器视觉技术的发展，给机器人缝纫技能学习带来了便利[13]：ZACHARIA等基于视觉伺服技术，将视觉反馈和神经网络与模糊逻辑相结合，使用自适应神经模糊推理系统进行调优，获得更好的估计[14]。综合神经网络的学习能力和遗传算法的优化能力，可应对缝纫过程中的不确定性、主观性、模糊性[15-16]。HUANG等采用立体视觉系统，对比理想针位置和实时针的三维点模型，使针驱动器自适应针姿态的变化，机器人自适应地跟踪针的姿态并实时调整学习的缝纫动作[17]。以上机器人技能学习方法，依靠神经网络系统控制参数并存储缝纫先验知识，使机器人获得作业技能。但是，这类方法存在着在线修正权值计算量大、权值过度修正，导致系统出现剧烈振荡以及抗环境扰动滞后等问题[18]。因此，人工智能与深度学习方法逐渐被应用于机器人技能学习领域[19]。徐文霞等运用深度相机采集用户的姿态信息，通过Kalman滤波方法预测用户状态，通过更新Kalman增益参数，机器人获得预测用户姿态的学习能力[20]。穆欣伟等采用双目视觉技术及深度学习目标检测算法对操作者手部进行识别与定位，建立操作者手部与机器人末端之间距离以及电机速度控制间的映射关系，使得机器人可根据距离自主执行减速、急停等操作的学习能力[21]。

机器人应用视觉传感器观察人类缝纫动作，生成示教运动轨迹的精度以及动作或技能特征参数的准确度，是机器人技能学习的首要条件[22]。机器人在动力性和可重复性等方面比人类有很大的优势[23]，机器人学习并跟随工人的缝纫动作，在提升缝纫机器人自动化程度和节约人力资源方面具有较大的应用价值。本文使用GMM对深度神经网络获得的动作轨迹以及时间因素进行编码，获得运动基元，运用GMR计算每段运动基元的均值函数和方差函数，将得到的高斯回归函数混合加权，预测轨迹回归。通过仿真实验验证了本文方法的平稳性和有效性。

1 缝纫动作识别方法

人工缝纫动作中的运动信息由关节运动轨迹体现。如何准确定位工人缝纫动作视频序列中的肩、肘、腕关节，并获取关节的运动轨迹，是机器人学习缝纫动作的关键。在布料翻转等动作中，由于工人动作习惯问题，常出现部分上肢或者手部被布料遮挡的情况，关节定位失败。本文改进了OPENPOSE姿态估计模型，运用标签融合方法更正关节点标签，获得缝纫动作中工人的完整关节信息。

1.1 基于OPENPOSE的关节定位

OPENPOSE模型采用了VGG-16深度学习网络以及双通道CNN残差网络结构，如图1所示。VGG-16的前10层网络获得了动作图像的原始特征图F(feature maps)，其后连接了多个称为阶段(stage)的子网络，每个阶段的Convolution部分是3个3×3卷积核所组成的残差网络结构。在提取深层特征信息和空间纹理信息的同时，也会保留部分浅层信息；其中Max Pooling使用1×1卷积核，使得网络变得更深以提取更高层特征。实验证明，6个阶段能在避免过拟合的前提下使模型达到最快收敛。每个阶段的输出和特征图F一起送到下一个阶段进行运算，经6个阶段之后输出关节定位结果。

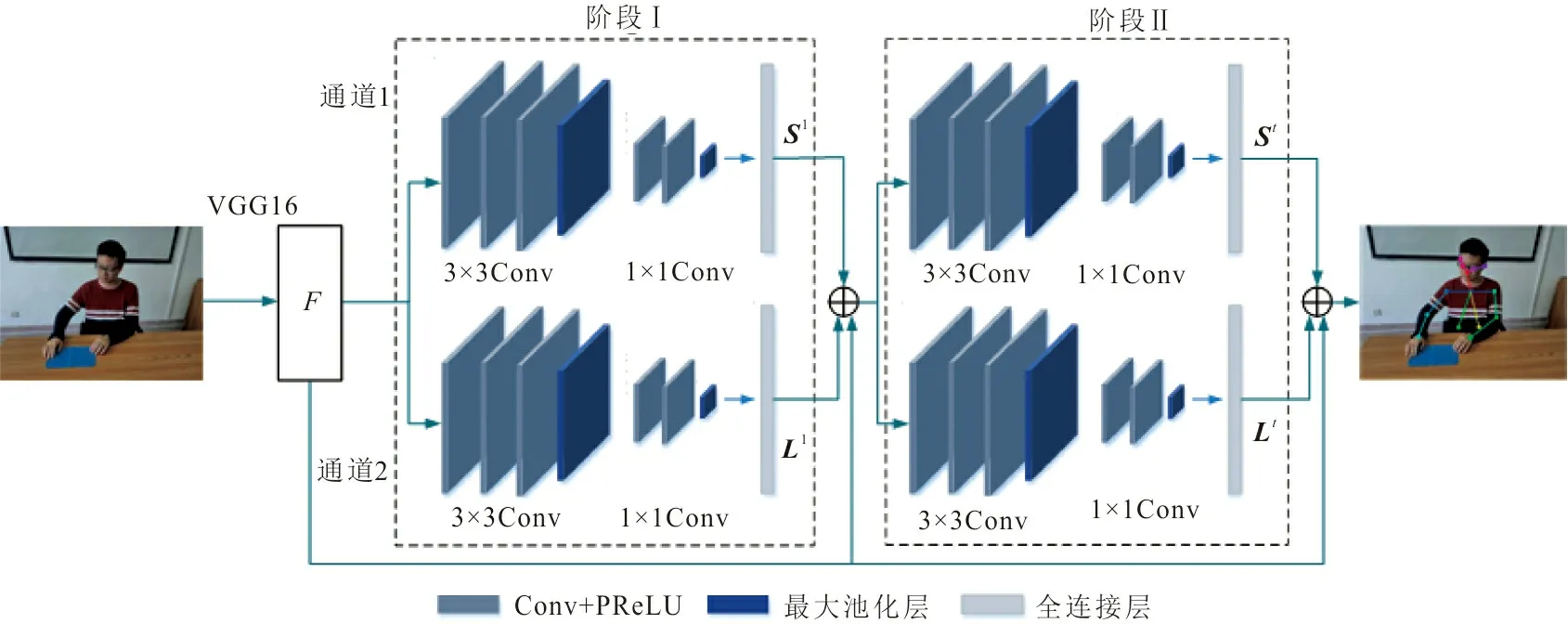
图 1 姿态特征提取过程Fig.1 Pose feature extraction process

OPENPOSE模型结构卷积核数目如表1所示。表1中，C1～C5代表单个通道CNN中各卷积层的卷积核数目，F代表直接输出的特征图部分，Ⅰ～Ⅵ代表双通道CNN结构的6个阶段。

表 1 OPENPOSE模型结构卷积核数目

OPENPOSE模型的2支CNN通道分别预测关节和肢体的位置。通道1预测关节点的位置，该位置用置信度的大小表示。置信度值为像素距离关节点的高斯响应，距离关节点越近的像素，响应值越大。运用非极大值抑制(non-maximum suppression，NMS)算法得到所有高斯响应中的峰值作为该阶段网络输出，记为S1；通道2预测关节点的亲和域。亲和域表示肢体位置和肢体上像素的方向，记为L1。若像素点在肢体外，则L1=0; 若像素点在肢体上，xj1、xj2等2点之间的L1=(xj2-xj1)/‖xj2-xj1‖2。

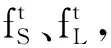
(1)

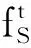
(2)

1.2 OPENPOSE的改进

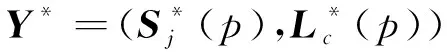
(3)

标签更正后的损失函数为

(4)

为验证改进模型的有效性，进行人体动作识别对比实验。采用COCO人体骨骼框架数据集进行模型训练，使用平均精度均值PMA作为精度评价指标，表示所有关节点的平均定位精度；使用每秒测试的图片帧数F*作为时间评价指标。几种模型对比结果见表2。

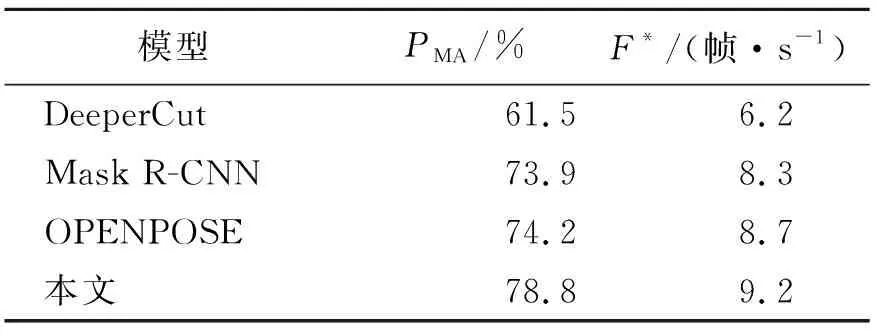
表 2 不同模型在COCO人体数据集上的结果对比

由表2可见：本文方法相对于DeeperCut，在精度上提高了17.3%，F*值提高了3 帧·s-1；与Mask R-CNN相比，在精度上提高了4.9%，F*值提高了0.9 帧·s-1；相较于OPENPOSE，在精度上提高了4.6%，F*值提高了0.5 帧·s-1。图2为改进前后的人体上肢关节识别结果。

(a) 改进前 (b) 改进后图 2 改进前后的模型识别效果对比Fig.2 Comparison of the recognition effect of before andimproved models

图2可以看出：改进后的模型能够更正关节点标签，重新定位右手腕关节，并建立与右手肘关节的肢体连接，成功识别人体右侧手臂。

2 机器人缝纫动作学习方法

基于GMM-GMR的机器人缝纫动作学习过程如图3所示。经OPENPOSE模型识别后，以获得的工人缝纫动作中上肢关节的坐标值作为训练样本，对训练样本进行节点聚类。采用GMM对时间因子和聚类节点进行混合编码，运用期望最大化算法求得聚类模型参数，使其基于历史数据模型概率达到最大化，得到代表高斯分量的聚簇，每一个聚簇代表一个关节。运用GMR对关节训练得到动作预测，根据预测误差不断更新模型的条件期望值和方差，期望值和方差即成为动作学习的参数。

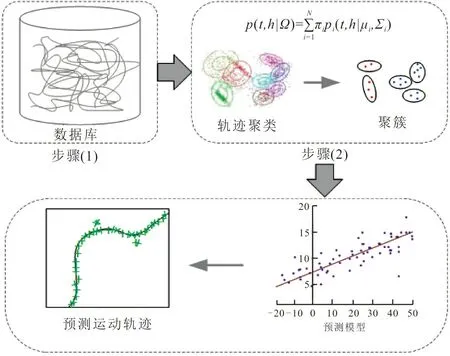
图 3 缝纫动作学习过程Fig.3 Sewing action learning process

2.1 GMM缝纫动作轨迹混合编码

为使机器人同时学习到关节运动信息和对应的时间信息，采用GMM对获取的缝纫动作轨迹进行混合编码。工人上肢缝纫动作包含肩、肘、腕等3个关节的运动轨迹信息。使用相同时间段t(t=1 000 ms)将每个关节的运动轨迹分割成数段运动基元，每段运动基元均表示一个关节缝纫运动的子过程。建立GMM模型Ω对每一段运动基元进行混合编码，每个基元以7个维度表示：一维的时间戳t和六维的机器人的关节姿态h={x,y,z,α,β,θ}。根据不同轨迹概率的比较确定预测轨迹，运用GMM建立n个高斯分量的联合分布概率密度函数，每个高斯分量均代表一段编码的运动基元，即

(5)

式中：t、h分别为模型Ω中运动基元的时间戳和关节姿态；πi、pi、μi和Σi分别为第i个高斯分量的先验值、条件概率密度、均值和协方差。

首先运用概率密度函数对缝纫动作轨迹数据进行建模，通过GMM对训练轨迹数据进行聚类分析。为提升算法收敛速度，使用K-means算法进行GMM初始化。采用期望最大化算法迭代计算至收敛，估计概率密度函数中的各参数；根据符合正态分布数据的条件分布，得到n个高斯分量的回归函数，用于GMR轨迹预测学习。

2.2 GMR缝纫动作轨迹预测学习

运用GMR计算每段运动基元的均值函数和方差函数，将得到的n个高斯回归函数混合加权，进行轨迹回归预测。通过更新学习轨迹参数中的条件期望值和方差，学习缝纫动作的轨迹信息，生成机器人的跟随动作的运动轨迹。

(6)

式中：

(7)

(8)

(9)

(10)

3 实验结果及分析

为了验证本文方法中机器人对缝纫动作的学习效果，由实验者做出示教缝纫动作，运用工业相机进行样本采集，提取上肢运动的样本信息进行轨迹学习的仿真实验，说明本文方法的可行性和学习效果。通过轨迹跟踪仿真实验，验证本文方法的平稳性和推广应用价值，并与Kalman轨迹预测方法的跟踪误差对比，验证本文方法的有效性。

3.1 缝纫动作识别实验

缝纫过程中常有 “移动布料”、“对齐布料”、“翻转布料” 等动作，实验者据此进行了3组示教缝纫动作演示。布料尺寸为260 mm×160 mm，六自由度机器人的工作半径为850 mm，符合机器人的工作空间范围。运用改进的OPENPOSE模型对示教缝纫动作进行姿态识别，图4(a)、(b)、(c)分别为3组示教缝纫动作的识别结果。识别成功后，记录每一个动作中人体右臂的肩、肘、腕关节的坐标变化，分别得到每个关节对应的缝纫轨迹，作为机器人学习的轨迹样本。

(a) 移动布料

3.2 缝纫动作学习仿真实验

OPENPOSE模型识别完成后，记录缝纫动作中右臂关节对应的坐标变化，分别得到人体右臂的腕关节、肘关节、肩关节的运动轨迹。缝纫动作轨迹如图5所示。

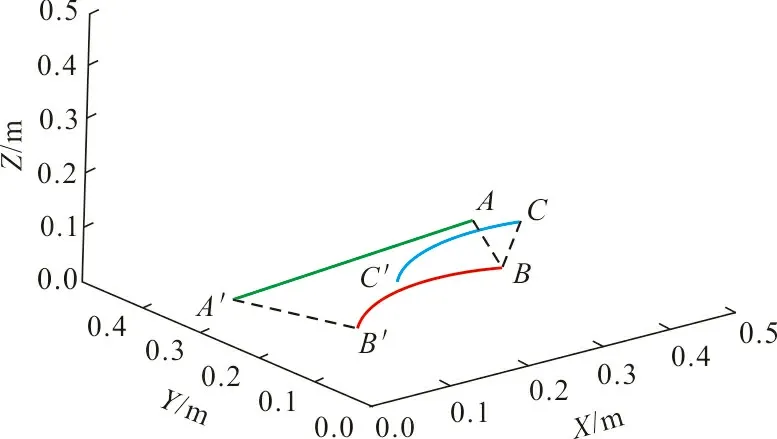
(a) 移动布料

图5中，绿色、红色、蓝色曲线分别代表腕关节、肘关节、肩关节的运动轨迹，A、B、C和A′、B′、C′点分别为腕关节、肘关节、肩关节的起始位置和终止位置。从图5可见：移动布料时，右臂的3个关节运动幅度均比较小；对齐布料时，腕关节在垂直方向的运动幅度明显增大；翻转布料过程中，3个关节在垂直方向的运动幅度均较大。符合现实中人体运动学特征。

运用GMM编码-GMR动作轨迹学习方法对每一条完整轨迹进行编码学习，得到的轨迹二维投影，如图6所示。图6中每一条二维曲线均代表图5中一个关节运动轨迹的学习结果：图6(a)对应“移动布料”中的肩关节运动轨迹，即图5(a)中的蓝色轨迹；图6(b)对应“对齐布料”中的腕关节运动轨迹，即图5(b)中的绿色轨迹；图6(c)对应“翻转布料”中的肘关节运动轨迹，即图5(c)中的红色轨迹。

(a) 移动布料

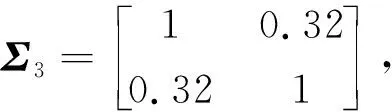
3.3 轨迹跟踪仿真实验

以“移动布料”中右臂的3个关节的运动轨迹为示例，在Simulink中搭建六自由度机器人的仿真模型，并进行机器人轨迹跟踪的仿真实验。经改进OPENPOSE模型识别获取关节点的二维像素坐标，通过视觉标定建立三维坐标映射模型，得到像素坐标系到机器人基座坐标系的转换关系，运用转换矩阵计算实现关节像素坐标到机器人三维坐标的映射，即得到机器人工作空间中的位置数据。将该位置数据组成的缝纫轨迹作为学习样本，通过GMM-GMR方法预测学习，得到样本缝纫轨迹的学习结果。将学习得到的位置数据转换成关节空间角度信息，分别将右臂的肩关节、肘关节、腕关节的空间角度信息输入到Simulink中机器人仿真模型的关节2、3、4中，机器人根据输入角度运动至期望位置，实现机器人对示教缝纫轨迹的跟踪。图7为轨迹跟踪过程中机器人对应的关节力矩变化曲线，该曲线由Simulink仿真环境中的编码器采集。

由图7可见，机器人的2、3、4关节力矩曲线在轨迹跟踪开始时均有较大幅度的波动。原因是机器人由静止进入运动状态的瞬间，惯性作用使机器人关节产生轻微的抖动。在0.5 s之内，各关节的力矩曲线均趋于平稳，说明机器人关节根据期望角度可以平稳地运动，证明了本文方法的平稳性。从关节力矩变化曲线可以得出，应用本文方法能实现机器人连续平稳地进行缝纫跟随运动，在节约人力资源方面具有一定的推广应用价值。

图 7 关节力矩变化Fig.7 Curve of joint torque change

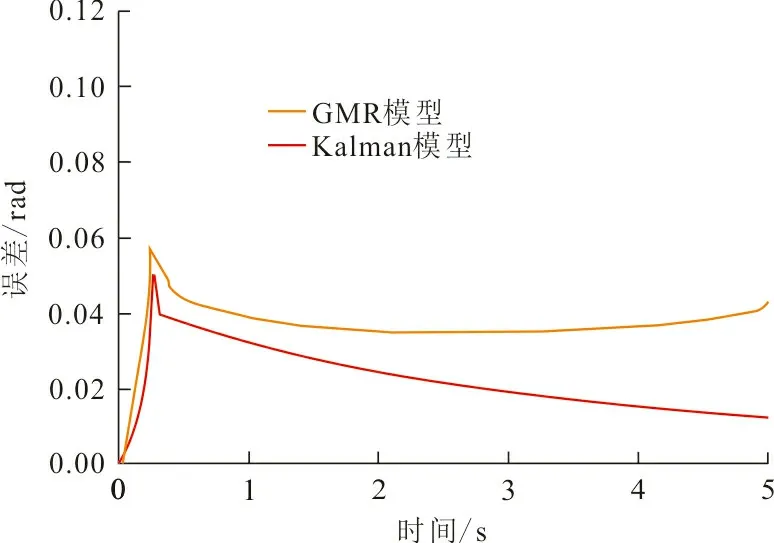
为进一步验证本文方法的有效性，将本文方法与Kalman预测方法进行轨迹跟踪仿真实验对比。运用Kalman方法预测轨迹插值过程中的关节角度数据，根据当前的关节角预测下一步的关节角，并根据每一步关节角的预测值和测量值求出最优值，从而生成目标关节角的变化曲线。图8为机器人运动跟踪过程中，关节2、3、4的轨迹跟踪曲线，图9为对应的误差曲线。从图8、9可以看出，与Kalman模型相比，GMR模型轨迹跟踪误差更小。

(a) 关节2

(a) 关节2

由关节2、3、4的轨迹跟踪曲线及误差跟踪曲线可见，机器人在运动的初始阶段关节会产生约0.052～0.087 rad的误差。原因是机器人从静止状态进入运动状态的瞬间，运动的关节会产生较大幅度的抖动从而对轨迹跟踪造成干扰。对比各关节中Kalman模型和GMR模型的误差跟踪曲线，2 s后Kalman模型的跟踪误差明显增大。原因是Kalman模型对短时间内的预测有比较稳定的判断，无法有效处理长时间的有噪声轨迹数据。GMR模型的跟踪误差随时间的增长呈下降趋势，且其准确性高于Kalman模型。在关节2、3、4的跟踪误差曲线中，对比GMR模型与Kalman模型在0～1 s内的误差变化，可以看出GMR模型可以在更短时间内降低跟踪误差，这是因为GMR模型加入了时间变量，考虑了机器人随时间运动的连续性。对比误差跟踪曲线可以看出GMR模型的准确性和可靠性均优于Kalman模型，证明了本文所提出的方法具有更好的实时性与学习能力。

4 结 语

本文提出了一种基于GMM-GMR的机器人缝纫动作学习方法。通过搭建并改进OPENPOSE模型，对上肢缝纫动作进行了有效识别。将上肢动作的各关节轨迹信息，映射到机器人各关节，采用GMM对缝纫运动轨迹进行混合编码，通过GMR方法进行参数学习，进而生成机器人关节的跟随运动轨迹。经机器人缝纫动作识别学习实验、缝纫动作学习仿真实验和Kalman方法轨迹跟踪对比仿真实验，结果验证了本文提出的方法能够有效地实现对人体上肢缝纫动作的跟踪，证明了本文方法的平稳性，且其运动精度可靠性、准确性均优于卡尔曼法，具有一定的推广应用价值。