基于NSCT 和卷积稀疏表示的红外与可见光图像融合*

魏亚南 曲怀敬 王纪委 徐 佳 张志升 谢 明 张汉元

（山东建筑大学信息与电气工程学院 济南 250101）

1 引言

红外与可见光图像融合是多传感器图像融合领域重要的研究内容。红外图像具有全天候工作，抗干扰能力强的优点，但同时存在对比度低、可视性差、等缺点。可见光图像传感器利用光的反射来获取图像，可见光图像具有光谱信息和细节信息丰富、可视性好等特点，但是其抗干扰能力比较差，在光线模糊或雾霾天气等情况下，可见光图像的效果会比较差。由此可见，仅使用一种图像传感器不能完整的展现出现实场景中的全部内容，因此需要将两种图像进行融合，综合两者的的优点，来获取一幅图像信息量丰富、视觉效果好的融合图像。通常，对于同一场景，红外与可见光图像具有互补性，它们的融合结果能够可靠和较好地保持源场景的显著特性。目前，红外与可见光图像融合广泛应用于检测、目标识别、安全监控、遥感等领域，而且在公安敏感目标跟踪识别、周界防护、事故鉴定取证等方面也发挥着重要的作用［1］。

近年来，在各类图像融合领域提出了多种融合方法。一般来说，这些方法可分为两大类：空域方法和变换域方法［6～7］。空域方法通常利用图像块或像素梯度信息来解决融合问题。这类方法通常更适用于源图像来自同一类型传感器的融合任务，例如，Aslantas［5］等提出一种通过使用差分进化算法寻找最优块大小的多聚焦图像融合方法，它有效地提升了融合图像的质量。在此类的红外与可见光图像融合方法中，基于像素加权平均的融合方法是比较常用的方法［2］。其基本思想就是将源图像各个位置的像素值进行加权平均，得到的值作为融合图像的相应位置的像素值。但是，由于这些方法直接对各个像素进行处理，没有充分考虑红外图像和可见光图像的成像差异，因此在融合过程中丢失一些细节信息，从而造成最终的融合图像对比度降低、融合效果不佳。对于这些不足之处，在本文研究中将得到改进。

变换域方法是各类图像融合中最常用的方法。变换域方法主要包括以下两类：一是基于多尺度变换（MST）的方法，这些变换包括Contourlet 变换［7］、非下采样轮廓波变换（NSCT）［3］、拉普拉斯金字塔（LP）［13］、Curvelet变换（CVT）［10］、离散小波变换（DWT）［14］和双树复小波变换（DTCWT）［15］等；二是基于稀疏表示的方法，包括卷积稀疏表示（CSR）［11］和自适应稀疏表示（ASR）［12］等。然而，在基于多尺度变换的图像融合方法中，通过拉普拉斯金字塔变换融合的图像在某些区域容易模糊，从而丢失细节和边缘信息；小波变换虽然在捕获图像的局部特征方面是有效的，但是由于其所刻画的方向信息不足，因此融合图像的边缘容易模糊和出现伪影；Curvelet变换在保留图像边缘和轮廓信息方面是有效的，但在表示融合图像某些局部信息方面存在不足；NSCT 变换虽然在描述方向性信息方面优于小波变换，且解决了Contourlet 变换缺乏平移不变性的问题、以及基本消除了伪吉布斯伪影，但是在细节信息捕获方面表现不佳，并容易导致融合图像中对比度信息的损失。在基于稀疏表示的图像融合方法中，普遍存在细节保留能力有限的问题。虽然基于CSR 的融合方法解决了图像融合中的细节模糊问题，但通过CSR进行红外与可见光图像的融合会导致低对比度和低亮度区域出现［17］。而且，这种方法通常只应用“平均规则”和“方差规则”来融合基本层或细节层，因此容易造成融合图像模糊、对比度降低。对于上述方法的主要不足，本文研究将进行改进。

为了解决上述图像融合方法中存在的细节信息丢失的不足，特别是红外与可见光图像融合时所出现的细节模糊、对比度低等问题，本文提出了一种基于NSCT、CSR 和导向滤波（GF）的红外与可见光图像融合方法。首先，源图像通过采用NSCT 分解为高频子带和低频子带。然后，低频子带采用CSR 来表示，以更好地保持细节，并按照choosemax 规则对低频子带系数进行融合。同时，通过导向滤波对高频子带进行结构信息优化，以更好地保留高频子带的细节信息，并通过选择最大值策略进行高频子带系数的融合。最后，通过逆NSCT 变换得到融合图像。本研究针对三组典型的红外与可见光源图像进行融合实验，实验结果表明了本研究可以较好地克服基于NSCT融合方法存在的细节捕捉能力不足、以及基于SR 融合方法存在的细节保留能力有限和对误配准的敏感性高的缺点，并验证了本文方法的有效性和可行性。

2 相关工作

2.1 NSCT变换

非下采样Contourlet 变换（NSCT）是在Contourlet 变换的基础上提出的［2］。它不仅具有Contourlet变换的多尺度和多方向特性，而且还具有平移不变性。通常，在基于多尺度变换域进行图像融合时，NSCT 能够有效地克服Contourlet 变换所引起的伪吉布斯效应，因而广泛应用于红外与可见光图像融合领域。具体地，NSCT 的分解结构示意图如图1所示。

图1 非下采样Contourlet变换的组成框图

NSCT 的基本结构分为非下采样金字塔（Non-subsampled Pyramid，NSP）分解和非下采样方向滤波器组（Non-subsampled Directional Filter Bank，NSDFB）两部分。首先，源图像采用NSP进行多尺度分解，在第一层得到低通子带图像L1 和高通子带图像H1。然后，将高通子带图像H1 通过NSDFB 分解为多个方向的带通子带图像，这样源图像就实现了多方向的分解。最后，对每层的低通子带图像重复上述操作，从而实现源图像的多尺度、多方向子带分解［19］。另一方面，NSCT的重建过程与分解过程可逆，在此不再赘述。由图1 可见，在NSCT 对源图像进行分解的过程中，由于没有经过采样操作，因此它具有平移不变性，并能较好地避免吉布斯伪影的出现；同时，所有方向子带图像的大小与源图像相同。

2.2 卷积稀疏表示

卷积稀疏表示可以看作是传统稀疏表示的卷积形式，卷积稀疏表示可实现对整幅图像的优化处理，这样就可以得到整幅图像，而不是部分稀疏表示的图像块。其基本思想是把图像看作一组系数映射和一组字典滤波器之间的卷积和。卷积稀疏表示模型通常可描述为［6］

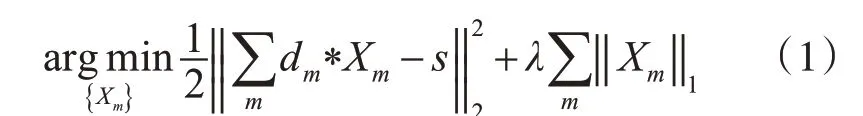
式中，*表示卷积算子；S表示整幅图像；λ为此模型的正则化参数，{dm}为M 个字典滤波器的集合，m∈{1,2…,M} ；{Xm}为稀疏系数集合。由于CSR是一种有效的全局图像表示形式，因此相比于SR，它可以使红外与可见光图像在融合的过程中保留更多的边缘和纹理细节信息。

2.3 导向滤波

导向滤波器（GF）［16］是近期提出的一种非常有效的边缘保持滤波器，且其计算时间对滤波器的大小不敏感。导向滤波器的工作原理可用式（2）的局部线性模型表示。

式中，I 表示引导图像；Q 表示滤波器输出；wk为以像素k 为中心的局部窗口，其半径用r 表示；ak和bk为模型的待定线性系数。通常，系数ak和bk可根据最小化式（3）所定义的准则函数，由线性岭回归方法计算得到，如式（4）和（5）所示。

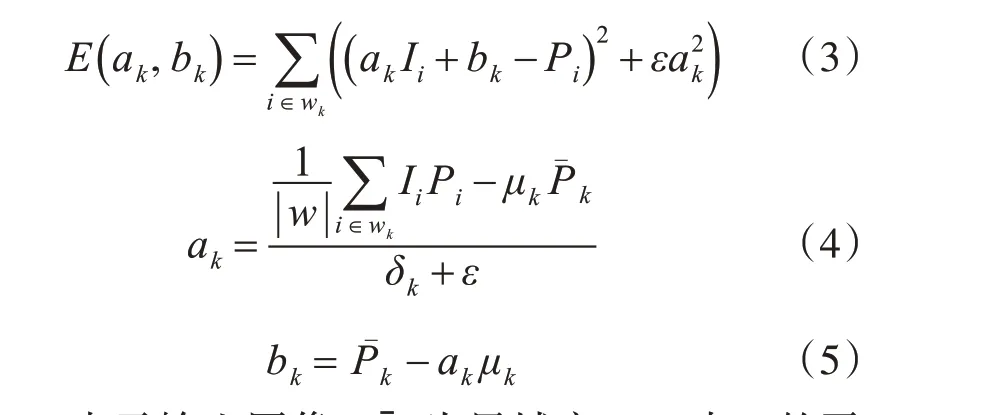
式中，Pi表示输入图像；Pˉk为局域窗口wk中Pi的平均值；μk和δk表示引导图像I 在局域窗口wk中的平均值和方差；ε为正则化参数，用来描述导向滤波后图像的模糊度；|w|为窗口wk中的像素数。

与其他保边缘滤波器相比较，导向滤波器是一种快速的线性滤波模型。由于它具有保真的几何结构迁移和平滑的边缘保持等显著特点，因此在图像融合等领域得到了广泛的应用［18］。

3 提出的融合方法

通常，基于NSCT 变换的图像融合策略为采用最大绝对值准则对高频NSCT 分量进行融合，采用“平均”准则对低频NSCT 分量进行融合。然而，由于可见光图像和红外图像具有不同的成像机制，低频分量的平均可能导致部分能量信息损失，从而降低融合图像的对比度。而基于SR 的图像融合方法细节保留能力有限，容易导致融合图像模糊和出现较多的伪影。虽然基于CSR 的图像融合方法解决了融合图像中的细节模糊问题，但其用于红外与可见光图像融合时会导致对比度和区域亮度降低。为了很好地解决上述问题，并结合NSCT 变换和CSR 互补的优点，本文首先运用NSCT 变换对图像进行多尺度、多方向分解，即把每个源图像都分解成低频子带部分和高频子带部分；然后，结合GF和CSR 模型，针对不同的子带部分运用不同的融合规则进行融合；最后，融合后的低频子带部分和高频子带部分通过逆NSCT 变换进行重构，最终得到融合图像。本文提出的具体融合方案如图2所示。

根据图2 所示的图像融合方案，本文采取的详细融合步骤如下。

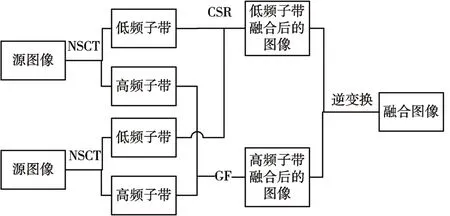
图2 本文提出的融合方案

1）采用NSCT 变换分解源图像，分别得到低频和高频子带。

2）高频子带系数的融合结合导向滤波GF，采用选择最大值法。首先，对高频子带进行导向滤波处理，即将高频子带作为导向滤波的输入而获得滤波图像；然后，采用“choose-max”策略得到融合后的高频子带系数。

3）低频子带系数的融合选用CSR 融合方法。首先，将两个源图像的低频子带分别用CSR 表示。其中，稀疏系数图Ck,m可以通过最优化计算式（6）的CSR模型得到。

4）通过选用适当的逆NSCT 变换，对融合后的高频和低频子带部分进行重构，以便得到最终的融合图像。

4 实验与讨论

4.1 融合性能的评价指标

为了综合评价不同图像融合方法的性能，采用定性和定量比较机制是非常必要的。在本文中，定性分析采用融合图像的主观效果比较。而定量分析采用公认的信息熵、平均梯度、均方差、标准差、峰值信噪比和结构相似度（SSIM）等六个客观评价指标进行比较。其中：

1）信息熵（E）用来描述图像所包含平均信息量的大小。其值越大，表明信息量越丰富。信息熵的定义为

式中，f（x，y）为图像在（x，y）处的像素的灰度值，M×N为图像尺寸。μF为图像的平均灰度值。

4）峰值信噪比（PSNR）反映图像的失真情况。其值越大，代表图像失真越小，图像融合的效果越好。峰值信噪比的定义为

式中，μ为图像的平均灰度值，σ为图像的标准偏差，C1，C2为常数。

4.2 定性的融合性能比较

本文将选用三组典型的红外与可见光图像数据进行融合实验，以验证所提出的融合方法的有效性和可行性。通常，融合性能优劣的定性分析是根据融合图像的主观效果进行评价。因此，为了更好地对本文方法的融合效果进行定性评价，对三组源图像分别采用导向滤波的方法（GF）［18］、卷积稀疏表示的方法（CSR）［11］、双树复小波与卷积稀疏表示相结合的方法（DTCWT-CSR）［17］、基于NSCT 变换与稀疏表示通用融合框架的方法（NSCT-SR）［16］、基于离散小波变换与稀疏表示通用融合框架的方法（DWT-SR）［16］和本文提出的方法实施融合实验，并进行对应的融合图像主观效果比较。

第一组实验采用的红外与可见光源图像如图3（a）和（b）所示。具体的融合实验结果如图3（c）～（h）所示。

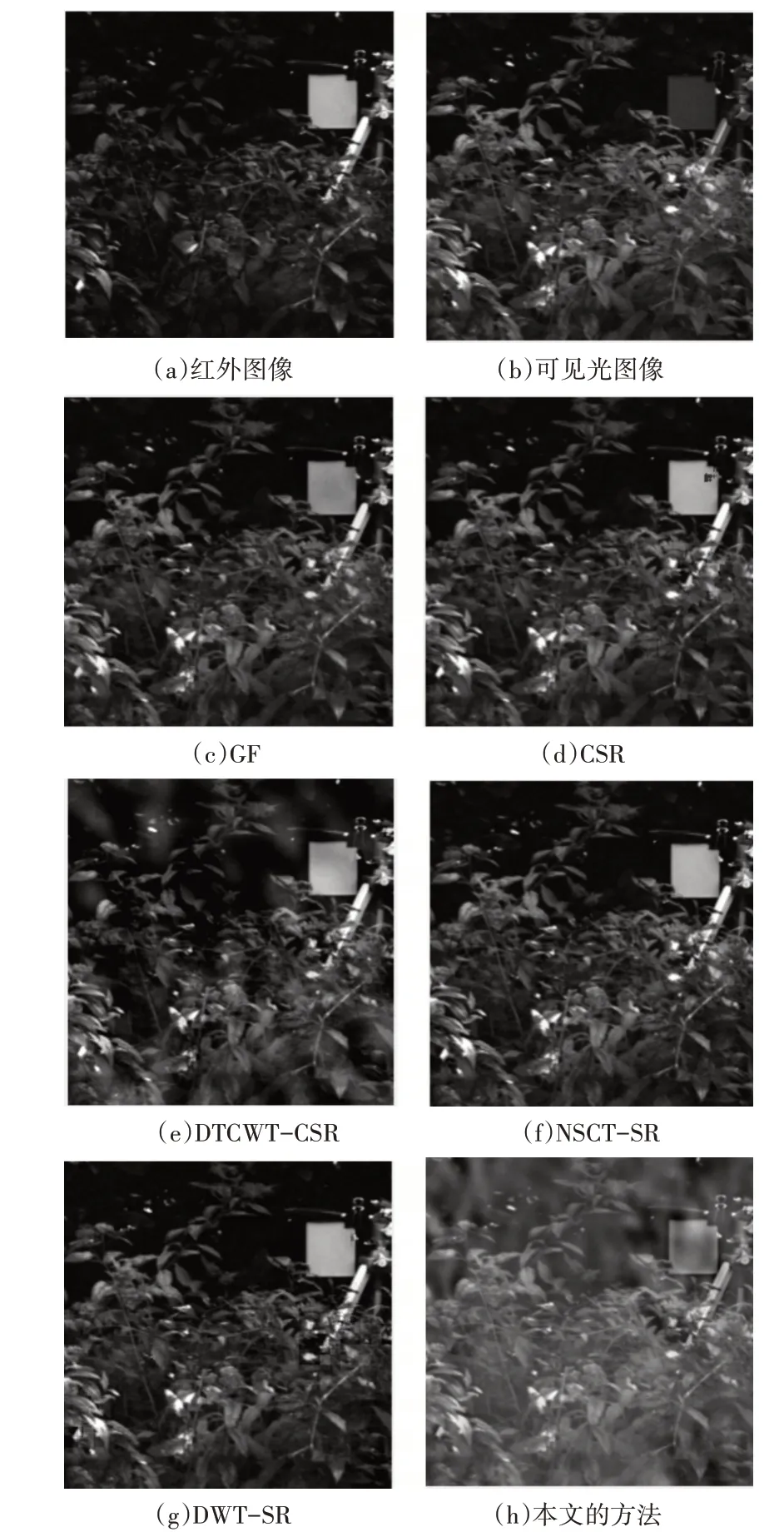
图3 针对第一组实验的融合图像效果比较

在本组实验中，图3（a）、（b）分别为红外与可见光源图像“树叶”。由图3（a）、（b）可见，在“树叶”图像的矩形块区域中，可见光图像保留了树叶的图像信息，但导致低目标对比度，这使得难以区分图中矩形目标；而红外图像高亮显示目标，但目标左侧的一些叶子没有呈现清楚。图3（c）～（h）是由上述各种方法分别得到的融合图像。由图可见，本文方法所得到的融合图像可以清楚地看到融合了两幅源图像的细节信息及阴影部分，尤其是在左上方的树叶轮廓及信息呈现的结果比其他几种方法融合的图像更加清晰。因此，从视觉效果来看，由本文方法得到的融合图像比源图像更具有可视性，也比其他方法得到的融合图像具有优越性。

第二组实验采用的可见光与红外源图像如图4（a）、（b）所示。具体的融合实验结果如图4（c）～（h）所示。

图4 针对第二组实验的融合图像效果比较

在本组实验中，图4（a）、（b）分别为可见光与红外源图像“树林”。由图4（a）、（b）可见，在“树林”图像的矩形块区域中，红外图像保留了树林的图像信息，但导致目标对比度低，这使得难以区分图像中白色板与后方的树林；而可见光图像中白色板的信息比较明显，但在图像中后面的一些树木的信息呈现得比较模糊。图4（c）～（h）是几种不同融合方法针对这两种源图像而得到的融合图像。由图可见，GF 和DTCWT-CSR 方法融合的图像仅强调目标周围的红外信息，导致图中的矩形块区域与后方的树林有些难以区分；CSR和DWT-SR方法产生的融合图像在图像上方天空显示一些“补丁”，而NSCT-SR 方法保留了两幅源图像白色板的信息，但其在融合图像中的呈现却是扭曲的。相比较地，本文方法得到的融合图像既保留了可见光图像中白色板的信息和红外图像中树林的信息，又提高了对比度，从而可以清楚地区分出白色板和树林。因此，本文提出的方法在融合图像的视觉效果上比其他几种方法更具有优越性。

第三组实验采用的可见光与红外源图像如图5（a），（b）所示。具体的融合实验结果如图5（c）～（h）所示。

图5 针对第三组实验的融合图像效果比较

在本组实验中，图5（a）、（b）分别为可见光与红外源图像“Kayak”。由图5（a）、（b）可见，在“Kayak”图像的中，可见光图像保留了马路、马路边栏杆及远处佛塔的细节信息，而红外图像房屋的信息比较清楚，但是远处的佛塔及马路边栏杆比较模糊。图5（c）～（h）是几种不同融合方法针对这两种源图像而得到的融合图像。由图可见，GF 和DWT-SR 融合方法仅强调了红外信息，远处佛塔的信息比较模糊，特别是DWT-SR方法呈现佛塔信息的地方显示出了一些“补丁”；而CSR 和NSCT-SR 融合方法产生的融合图像在佛塔及栏杆处的细节信息比较模糊，而且也出现了一些“补丁”。相比较地，由本文方法得到的融合图像既保留了可见光图像的细节信息，即可以清楚地看到佛塔，又保留了红外信息，即可以清楚地看到房屋及汽车的细节信息。因此，本文提出的方法比其他几种方法取得了较好的图像融合效果。

4.3 定量的融合性能比较

为了进一步验证本文提出的融合方法的有效性，与上述其他图像融合方法进行客观性能的比较。即，将信息熵、平均梯度、均方差、峰值信噪比和结构相似度等五个客观评价指标作为比较依据。

第一组实验的客观指标如表1所示。由表1的数据可见，相比于其他的融合方法，本文的融合算法在均方差、平均梯度和峰值信噪比三个指标上有明显的改善。其中，相较于DTCWT-CSR 方法均方差降低了86.09%，峰值信噪比提高了31.92%，平均梯度提高了10.11%；相较于NSCT-SR 方法均方差降低了84.19%，峰值信噪比提高了25.60%，平均梯度提高了7.01%；相较于CSR 方法均方差降低了84.70%，峰值信噪比提高了29.92%，平均梯度提高了14.67%；相较于GF 方法均方差降低了84.69%，峰值信噪比提高了26.24%，平均梯度提高了15.55%；相较于DWT-SR 方法均方差降低了83.64%，峰值信噪比提高了24.92%，平均梯度提高了2.79%。在表1 的实验数据中，本文方法在信息熵和结构相似度指标上较差一些，这主要是由所采用的稀疏字典引起的。然而，图3 和表1 的结论是一致的，说明本文的融合方法是有效的。

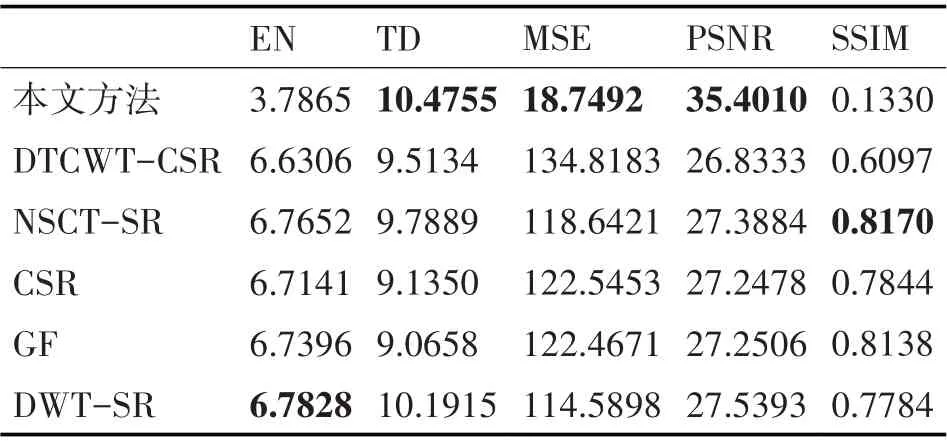
表1 针对第一组实验不同融合方法客观性能指标的比较

第二组实验的客观指标如表2所示。由表2的数据可见，相比于其他的融合方法，本文的融合方法在均方差、峰值信噪比和平均梯度三个指标上有明显改善。其中，相较于其它方法，本文的方法在均方差指标上均降低了90%以上，峰值信噪比指标也均提高了50%以上，平均梯度提高了10%以下。在表2 的实验数据中，本文方法在信息熵和结构相似度指标上较差一些，这也主要是由所采用稀疏字典以及NSCT 变换所采用的滤波器的性能引起的。然而，图4和表2的结论同样是一致的，说明本文的融合方法是可行的。

表2 针对第二组实验不同融合方法客观性能指标的比较

第三组实验的客观指标如表3所示。由表3的数据可见，相比于其他的融合方法，本文的融合方法在平均梯度、均方差和峰值信噪比等三个指标上有着明显的改善。相较于DTCWT-CSR 方法平均梯度提高了11.01%，均方差降低了91.56%，峰值信噪比提高了42%；相较于NSCT-SR 方法平均梯度提高了3.71%，均方差降低了74.71%，峰值信噪比提高了19.68%；相较于CSR 方法平均梯度提高了1.02%，均方差降低了12.78%，峰值信噪比提高了1.66%；相较于GF 方法平均梯度提高了16.57%，均方差降低了77.22%，峰值信噪比提高了21.5%；相较于DWT-SR 方法平均梯度提高了4.59%，均方差降低了7.63%，峰值信噪比提高了0.96%。在表3实验数据中，本文方法在信息熵和结构相似度指标上较差一些。这同样是由所采用的稀疏字典以及所采用的方向滤波器所引起的。然而，本文方法具有平移不变性，这有利于消除融合时的伪吉布斯现象，改善融合效果。同时，图5和表3的结论是一致的，说明本文的融合方法是有效的和可行的。

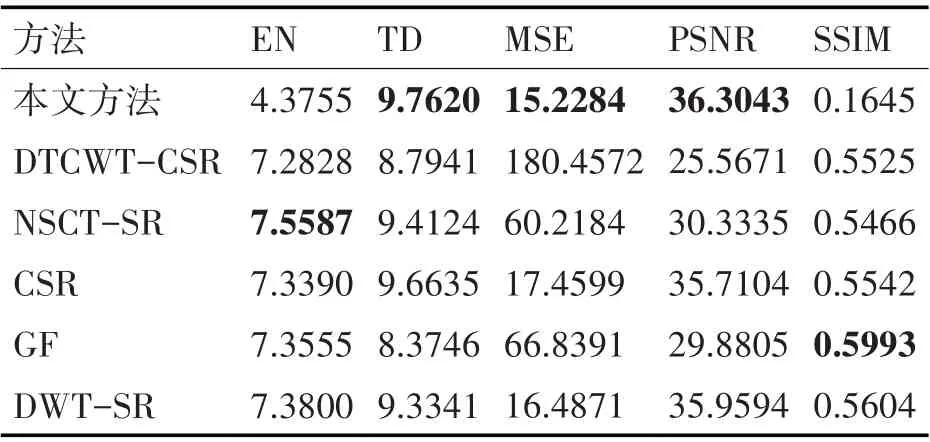
表3 针对第三组实验不同融合方法客观性能指标的比较

4.4 运行时间的比较

在进行了主观融合效果和客观性能指标的综合比较后，本文又通过对各个融合方法融合图像时所需的时间进行了比较，所得的实验结果如图6 所示。

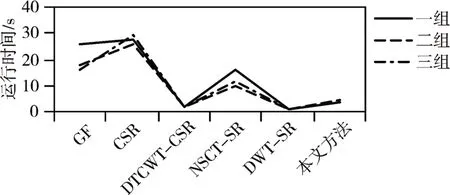
图6 不同融合方法运行时间的比较

由图6 的数据可见，GF 方法、CSR 方法和NSCT-SR 方法用于图像融合的时间远大于其他几种融合方法的时间，而本文方法在这几种方法中所用的时间是相对较少的。造成这种结果的原因是CSR 方法是从SR 中派生出来的。虽然CSR 方法的结果是全局性和唯一的，并可以用它来优化低频分量，但CSR 在整幅图像处理过程中还是相对耗时的。此外，单一基于窗口的导向滤波用于图像融合时的计算效率也不佳。因此，为了提高计算效率，本文提出了将NSCT 和CSR、GF 有机结合的方法用于图像融合。由图中数据可见，本文方法采用NSCT变换具有平移不变性，并能较好地避免吉布斯伪影的出现；同时，所有方向子带图像的大小与源图像相同，从而使图像处理更加方便。此外，它还具有方向选择性，从而保留了更多的纹理细节。特别地，它将NSCT 和CSR、GF 相结合可以很好地降低CSR 在低频段造成的低计算效率的影响。总之，本文方法所用的的融合时间较少，计算效率较高。

综合以上的定性和定量实验结果可见，本文方法通过将NSCT 和CSR、GF 有机结合，既提高了融合速度，又有效地保留了更多的细节信息，因此它是一种可行的和有效的红外与可见光图像融合方法。

5 结语

在本文中，提出了一种基于非下采样轮廓波变换（NSCT）和卷积稀疏表示（CSR）的红外与可见光图像融合方法。它既充分地利用了NSCT变换灵活的多尺度、多方向性以及局域性和平移不变性，又有机地与CSR 的全局性和导向滤波（GF）的结构信息增强性相结合，从而更好地改善了融合图像的视觉效果和保真质量、提高了融合过程的计算速度。特别地，红外与可见光源图像经过NSCT 多尺度分解成高频子带和低频子带后，对低频子带采用了基于CSR的融合方法，有效地减少了图像结构信息丢失、对比度和区域亮度降低等问题；对高频子带进行了GF 优化，更好地保留了高频子带的细节信息和减少了边缘伪影；而将NSCT、CSR 和GF 有机结合，更好地保真了图像的显著信息以及提高了融合计算的速度。实验结果表明，本文提出的方法是一种比较有效的红外与可见光图像融合的新方法。