Nagumo条件下四阶边值问题解的存在性

邓瑞娟

(芜湖职业技术学院基础教学部，安徽 芜湖 241003)

0 引言

自然界中很多现象都有微分方程与之相对应，因此对这些复杂微分方程解的研究一直都在继续，其中非线性常微分方程就是研究中的一大热点.非线性常微分方程被大量地应用于核物理、生物数学、动力学、弹性梁等各个领域，正是因为非线性常微分方程广泛的应用背景，对其解的研究引起了越来越多学者的关注.虽然绝大多数非线性常微分方程没有办法给出解析解，但只要有解的存在性结论，就可以运用数值方法得到方程的近似解.其中，对于二阶、三阶边值问题各界学者的讨论已经非常充分[1-5]，如邓正平[5]运用各种不动点理论，分别讨论了在非线性项f满足一次增长、超线性增长、次线性增长等不同条件下方程

u‴(t)+a2u″(t)+a1u′(t)+a0u(t)=f(t,u(t),u′(t),u″(t)),t∈R

的2π-周期解的存在性.

关于四阶边值问题研究也有一些成果[6-8]，如在文献[6]中，笔者运用特殊的导数估计技巧研究了方程

的四阶两点边值问题正解的存在性.

但是目前对于具有四阶常微分算子Lu(t)=u(4)(t)+a3u‴(t)+a2u″(t)+a1u′(t)+a0u(t)的边值问题

(1)

解的存在性讨论的并不多.本文受上述文献启发，在非线性项f满足一定的增长条件下，运用Leray-Schauder不动点定理讨论边值问题(1)解的存在性.

1 预备知识

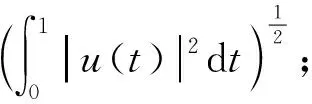
本文始终假设边值问题(1)满足如下条件：

(H1)对于∀M>0，都存在gM∈C+(R)满足：

(2)

使得f(t,x,y,z,w)对于(t,x,y,z,w)∈[0,1]×[-M,M]3×R，满足：

(H2)存在非负常数b0，b1,b2,b3，满足b0+b1+b2+b3+a2-a0<1,b1≥a0,C0>0,使得非线性项f(t,x,y,z,w)满足：

f(t,x,y,z,w)z≥-b0x2-b1y2-b2z2-b3w2-C0，(t,x,y,z,w)∈[0,1]×R4.

设h∈L2(I)，首先考虑如下四阶线性微分方程边值问题:

(3)

记P(λ)=λ4+a3λ3+a2λ2+a1λ+a0为四阶线性微分算子L对应的特征多项式.

引理1 假设P(2πki)≠0,k=0,±1,±2,…，对于∀h∈L2(I)，四阶边值问题(3)存在唯一解u=Sh∈H4(I)，且解算子S∶L2(I)→H4(I)为线性有界算子.

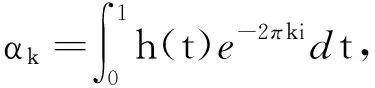
假设u∈H4(I)为边值问题(3)的解，则u(m),m=0,1,2,3,4,可展开为L2(I)中的傅里叶级数，根据傅里叶展开及其系数的相关公式u(m),m=0,1,2,3,4,可展开为

(4)

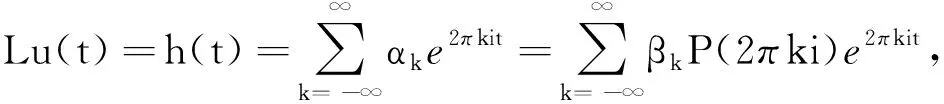
(5)

另一方面，对于∀h∈L2(I)易验证由(5)式确定的u(t)为线性方程(3)的解.综上所述，u=Sh为边值问题(3)的唯一解，且由(5)式可知，S∶L2(I)→H4(I)为线性有界算子.

证明 设u∈H4(I)为边值问题(1)的解，对引理1中(4)式运用Parseval等式，可得到

于是有

证明 假设存在M1>0，使得

(6)

在上述不等式两边乘以u‴(t),u‴(t)>0，可得到

对上式两端在[t2,t1]上积分，并在两端取ρ=u‴(t)，可得到

2 主要结果

定理1 假设P(2πki)≠0,k=0,±1,±2，…，连续函数f∶[0,1]×R4→R满足条件(H1)和(H2)，则边值问题(1)至少有一个解.

证明 假设F(u)(t)=f(t,u(t),u′(t),u″(t),u‴(t))，由f的连续性可知，F∶C3(I)→C(I)也连续，且把有界集映射为有界集.

定义算子A=S○F，其全连续性可由引理1及C4(I)→C3(I)的紧性直接得出.下面运用Leray-Schauder不动点定理证明边值问题(1)解的存在性.根据算子S的定义，只需证明A在C3(I)中存在不动点.为得出这一结论，考查同伦簇方程

u=λAu,λ∈(0,1).

(7)

设u∈C3(I)为方程(7)的解，其中，λ为(0,1)中某个特定的常数，则u=λAu=λSF(u)=S(λF(u)).根据S的定义，u即为方程(3)的唯一解，其中，h=λF(u).因此，u∈C3(I)满足如下方程：

u(4)(t)+a3u‴(t)+a2u″(t)+a1u′(t)+a0u(t)=λf(t,u(t),u′(t),u″(t),u‴(t)).

先将上述微分方程两端同时乘以u″(t)，然后在[0,1]上积分，再结合u(k)(0)=u(k)(1),k=0,1,2,3和条件(H1)，得到

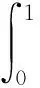
经过整理可得

(8)

结合(8)式并运用引理2，有

可见，u在H3(I)中有界.于是有

则同伦簇方程的解集在C3中有界，此时A中C3存在不动点，而该不动点即为边值问题(1)的解.

例1 考虑如下四阶边值问题：

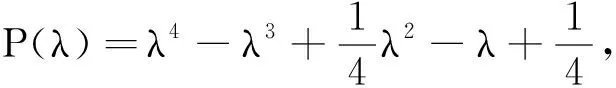
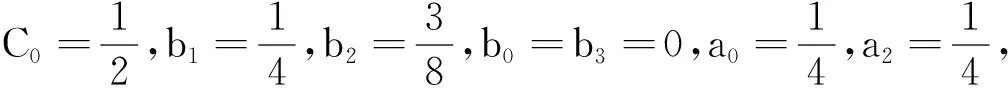
且b1≥a0,C0>0.由定理1可得，微分方程至少有一个解.

上述例题具有四阶线性常微分算子，同时非线性项f具有u″(t)和u‴(t)，因此，解的存在性结论无法从其他文献获得.