基于数字图像相关方法的霍普金森压杆测试技术

齐 娟,王 飞

(1.安徽理工大学电气与信息工程学院，安徽 淮南 232001;2.安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232001)

冲击动力学主要研究材料在动态加载条件下的力学行为，由于加载速率的增加会导致材料的力学性质和断裂行为发生变化。动荷载的来源形式主要包括爆炸、冲击和地震等事件，这些事件都是以质点加速度、速度和位移的时间历史形式存在的[1]。探讨材料在动态冲击下的动态力学响应对结构设计和防护等研究具有重要的现实指导意义。

关于材料力学行为的研究可根据试验加载应变率的大小分为蠕变、静态、准动态、动态、超动态试验。静态和动态试验之间存在一个根本区别，即惯性和波传播效应在较高的应变率下变得更明显[2]。图1显示了在各种加载试验所对应的应变率范围和相应的加载技术。由于工程材料在102～104s-1应变率加载范围内尤为敏感，因此人们更多地关注该应变率区间范围内材料的动态力学行为。而霍普金森杆正好能实现此应变率区间内的加载，且由于其结构简单、操作方便、加载波形易于控制，现已成为最常用、最可靠的测试材料在高应变率下力学行为的实验装置[3]。

霍普金森杆最早起源于1872年HOPKINSON设计开展的铁丝冲击试验[4]，该试验指出了冲击动力学的两个经典支柱效应，即应变率效应和应力波效应。与准静态不同，在研究材料在高应变率下的动态力学响应时，通常必须考虑材料的应变率效应和应力波效应(惯性效应)，而在实际情况中这两者通常是相互耦合、相互影响的，使研究的问题变得复杂。HOPKINSON[5]于1914年继续设计了飞片撞击试验，可以认为是霍普金森杆的初始雏形。后来TAYLOR[6]、DAVIES[7]和KOLSKY[8]等人通过对其进行不断的改进与完善，分离式霍普金森杆(又称为Kolsky杆)应运而生。霍普金森杆实验技术的巧妙之处在于其能将应变率效应和惯性效应解耦，在满足杆中一维应力波传播假设和试件应力沿其长度方向均匀分布假设的基础上，此时试件在高应变率动态加载过程中的应力应变曲线可通过测量杆中的脉冲波形计算得到。

然而传统的SHPB使用的接触式应变电测法存在一些不足和缺陷，现阶段人们开始更多地关注测量精度和可视化程度更高的数字图像相关方法。基于此，本文介绍了传统SHPB试验装置和原理，分析了应变电测法存在的一些不足和缺陷，并简要总结了数字图像相关方法在SHPB试验中的应用及其优势。

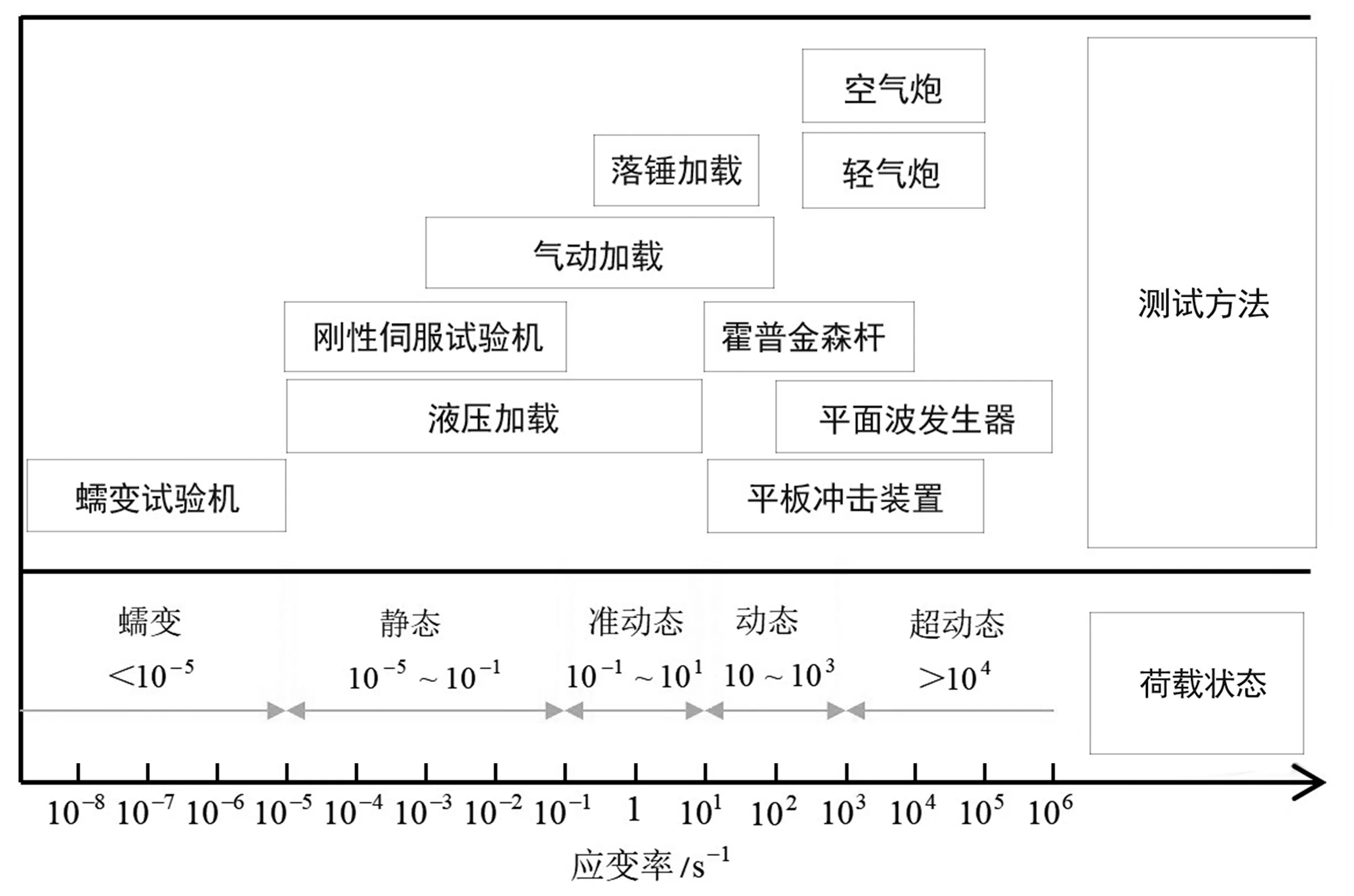
图1 加载试验所对应的应变率范围和对应的加载技术

1 传统霍普金森压杆测量技术

1.1 霍普金森压杆的分类

依据实验系统中有无透射杆，可将霍普金森压杆测试技术分为有透射杆的分离式霍普金森压杆(SHPB)测试技术和无透射杆的自由式霍普金森杆(FHPB)测试技术，其系统示意图分别如图2和图3所示。霍普金森压杆实验技术发展到现在已有百余年的历史，其在设计初期主要用于高应变加载下高聚物和金属类等均匀材料的动态力学性能测试的研究。然而现实生活中非均匀材料居多，如混凝土、岩石等，了解这类材料在冲击加载下的动态力学行为对工程设计和应用具有重要的现实指导意义。对于含夹杂物的非均质材料，以混凝土为例，其圆柱形试件的直径需大于粗骨料的4倍以上，故此时从宏观上能将其视为均质材料。为拓展霍普金森杆的适用范围，霍普金森杆的杆径必须相应增大以满足试件均匀性的要求。且伴随着试样设计规范的统一化和数据处理方法的改进，该项技术开始被广泛地应用于动态冲击下脆性材料和软材料的压缩性能测试。

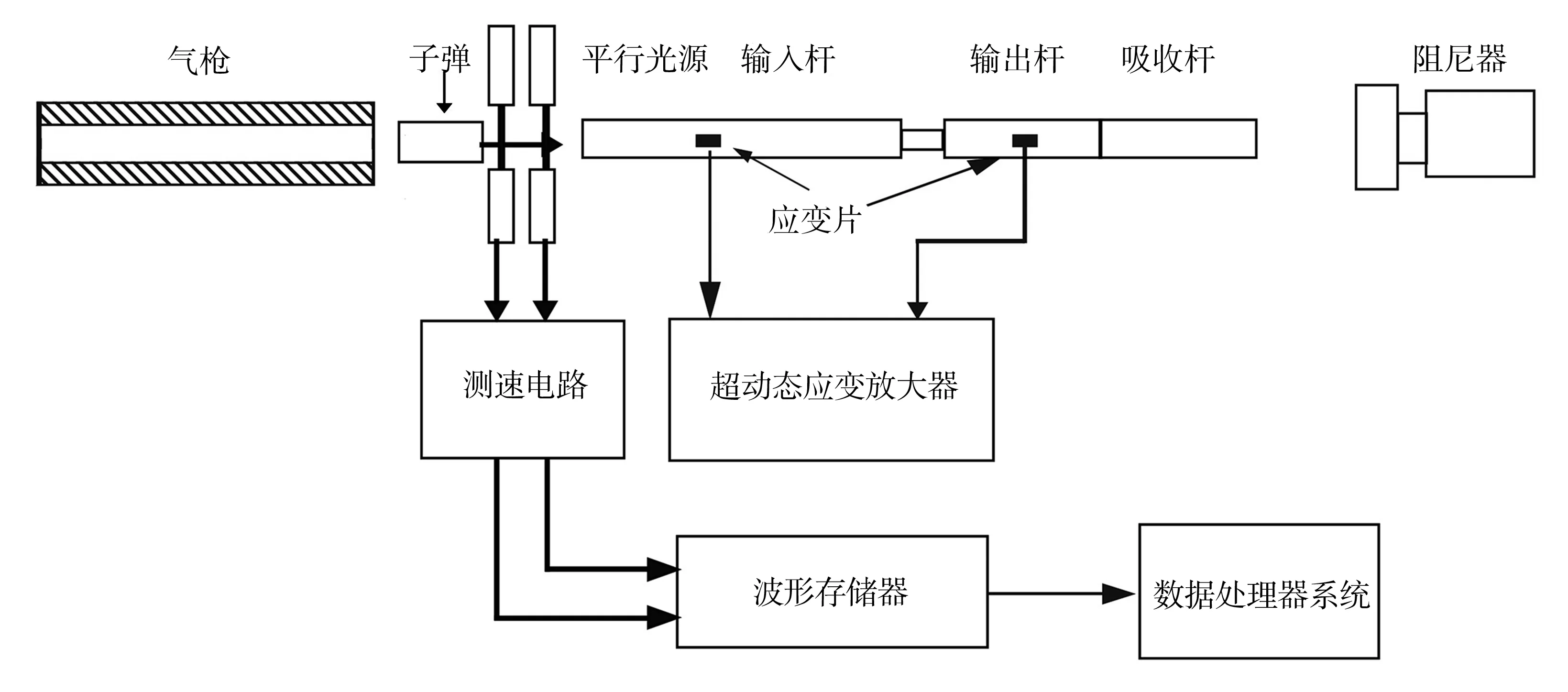
图2 分离式霍普金森杆

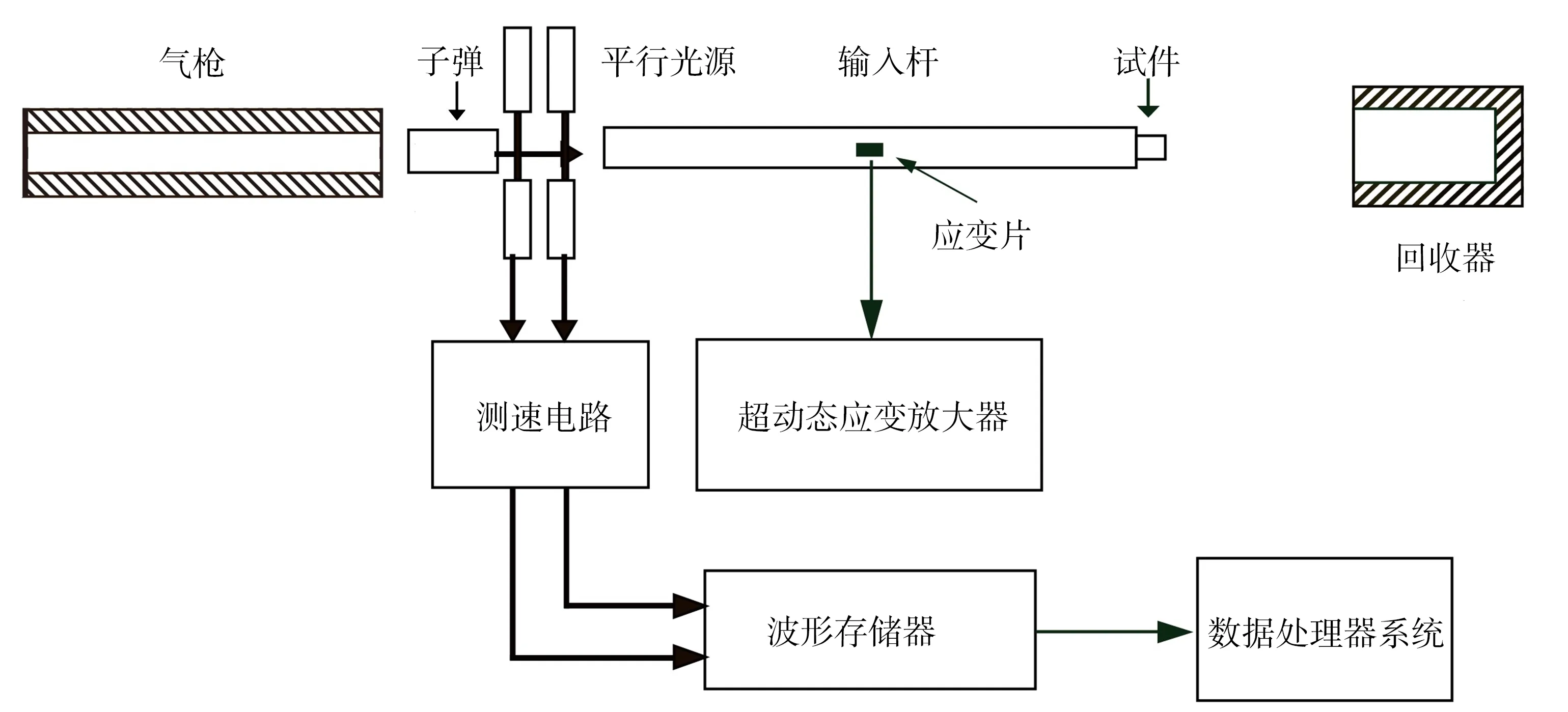
图3 自由式霍普金森杆

另一方面，随着分离式霍普金森杆的高速发展，自由式霍普金森压杆技术开始诞生。1983年SILL[9]首先将其运用于校准和标定高g值加速度传感器，随后TOGAMI等[10]对其进行了进一步的推广应用。美国PCB公司生产的FHPB高g值加速度传感器校准系统925A01的校准范围为1.0×103～1.0×105m·s-1。美国SDL实验室生产的FHPB加载试验装置能产生的加速度达1.5×105m·s-1[11]。李玉龙[12]、盛党红[13]等通过理论分析改进了利用FHPB标定高g值加速度传感器的方法，测得了高达2.0×105g的加速度峰值。邓强等[14]将利用FHPB对火工品的安全性和可靠性进行检验，得到了弹药不同的加速度脉冲波形。FHPB测试技术从初期校准加速度传感器线性度不高，发展到现阶段被广泛应用于评估和测试极高过载下火工品的抗过载性能，取得了长足的发展。

1.2 传统SHPB技术的测量原理

典型的SHPB实验装置通常由动力加载系统、弹性压杆系统和数据采集系统三部分组成，如图4所示。其中，动力加载系统包括气枪类驱动装置、密封环和子弹等，用以给整个实验装置提供初始动能；弹性压杆系统包括入射杆(反射杆)、透射杆以及用于吸收剩余动能的阻尼器等，实验中要求入射杆和透射杆为波阻抗相同的同质材料；传统的数据采集系统由粘贴在入射杆和透射杆上的应变片、示波器、电信号前置放大器以及数据记录处理系统等组成。

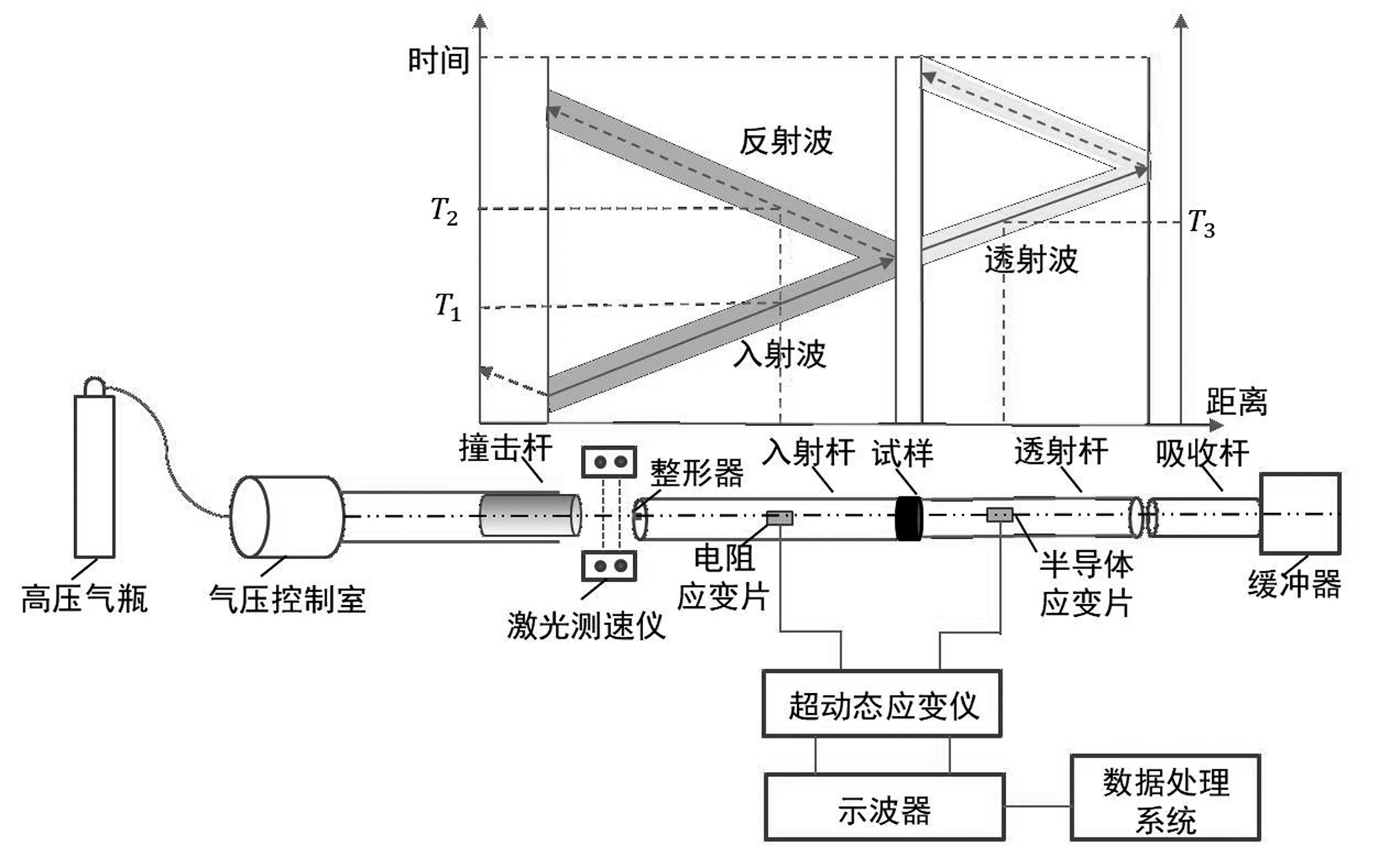
图4 分离式Hopkinson压杆装置

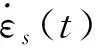
(1)

其中，A0和As分别为压杆和试件的横截面积；ls为试件的初始长度；E0和c0分别为入射杆的杨氏模量和一维应力波波速。

对试件引入均匀性假设，则式(1)可简化为

(2)

式(1)和(2)为经典的三波法和二波法测试数据处理公式。通常情况下，基于绝对时间下计算试件应力和应变的三波法具有较好的精度，能最大程度地避免处理数据过程中人为因素导致的误差。而当透射杆上的透射波信号相对而言较微弱时(如测试试件为软材料)，采用三波法处理数据时带来的误差可能会对结果产生较大的影响，此时可考虑采用简化后的二波法[15]。

1.3 传统应变信号量测

传统的应变信号量测是通过粘贴在入射杆和透射杆上的两组应变片实现的。现阶段最常用的应变量测方法有三种：电阻应变片法[16]、半导体应变片法[17]和聚偏四氟乙烯薄膜(PVDF)压电计法[18-19]，实物图如图5所示。电阻式应变法使用最为广泛，测量结果相对更为稳定，且其受温度的影响较小。但另一方面，其灵敏度较低，当反射波信号幅值较低时测量误差较大。相比之下，半导体应变片具有灵敏度较高、机械滞后小、横向应变小等优点，但其存在温度稳定性较差、较大应变作用下非线性误差大等弊端。PVDF作为一种新型的高分子压电型传感器，具有频响宽、瞬态响应时间短、噪音信号小等特点。相比于半导体应变片量测时噪声信号可能会掩盖应变的微弱信号，势必会导致量测波形失真[20]，此时PVDF的优势便凸显出来。三种应变计量片各有千秋，在试验过程中应根据实际需要选择合适的应变片。

(a)电阻应变片 (b)半导体应变片 (c)PVDF压电计图5 不同类型的应变计

传统的应变电测法促进了霍普金森压杆实验技术的长足发展，但随着科学的日益进步和人们对材料力学性能更精确的测量需求，其弊端开始显现出来。首先，应变片与压杆表面应具有良好的粘附性，否则这种接触式的测量方式会在很大程度上影响实验结果，并且其所能提供的测量精度有限；其次，应变片需直流电源驱动，且试验测得的应变值取决于单臂电桥的放大和测量信号的校准；再次，传统的应变片电测法对于杆径小于3 mm的SHPB试验无法使用，不能满足对微小尺寸材料在高应变率下动态力学响应进行测量的需求；最后，人们现更多关注于破坏的萌生和发展、变形局部化等问题，而传统的应变电测法无法观测材料的局部变形和细节特征，只能采取试验后效观测的手段对材料的破坏形态进行观察分析。

2 基于数字图像相关的SHPB试验技术

2.1 DIC测量原理

与高速摄像相结合的数字图像相关测试技术(Digital Image Correlation，DIC)，又称数字散斑相关方法(Digital Speckle Correlation Method，DSCM)，主要是通过测量试件表面上随机分布的每一斑点的位移，由此得到材料表面位移场，然后通过适当的滤波和微分得到相应的应变场。该非接触式应变测量法不需要力的平衡条件，也不需要均匀的应力-应变状态。DIC测试最基本的条件是在物体表面具有辨识度较高的特征点，为满足这一条件，一般需要人工在试件表面制作随机灰度分布的散斑场。也有学者在试验中利用激光照射试件形成激光散斑场，但因与高速摄像等互相干扰，使得实验条件复杂，此方法已被逐渐摒弃。人工制作散斑时先对试件表面打磨出纹路，然后喷射哑光漆或玻璃微珠漆形成随机散斑图案，散斑颗粒的大小控制在3～5个像素较为适宜。随机图案可以确保选取试件表面的任意小区域时是唯一的，用高速摄像采集试验前后的图案，采用相关算法便可追踪任一区域的变形场。该方法的分析技术主要包括图像的采集与提取、图像的相关计算和后处理三个部分，其中相关算法可分为三步进行：第一步，粗略估算整型量位移分量，计算精度保持在半个像素左右；第二步，根据确定的整型位移分量选取辨识度较高的新的变形小面，确定非整型量；第三步，采取可抵消非重叠小面之间相互关联的傅里叶级数展开位移技术，用以提高非整型量数据的精度，从而获得精确可信的散斑位移场。

2.2 DIC在SHPB试验中的应用现状

早在1914年在激光技术日益发展的大背景下人们开始关注散斑现象，目前公认是由美国的南卡罗莱纳州大学的PETERS和RANSON[21]于1982年最早将其应用于试件表面位移形变等信息的测量，与此同时日本的YAMAGUCHI[22]初步完成了干涉场和计量理论的相关研究。国内关于DIC的研究起步稍晚，始于20世纪90年代初[23]，中国科学技术大学的HAN等[24]提出将DIC技术应用于SHPB试验中，获得了碳钢和铝合金试件在冲击加载下不同时刻的散斑图像和应变场。DIC测量技术后续经历了理论分析、适用范围的扩展、相关迭代法的改善(灵敏度提高)、应变梯度影响因子的提出、分形数字散斑理论和亚像素方法的提出等过程。该方法自提出发展至今，由于具备可实现全场测量、非接触、高度自动化、精度高、抗干扰强、可实时监测等优点，现已被广泛应用于材料力学性能的测试。

PIERRON等[25]利用SHPB加载装置结合DIC方法对高应变率加载下混凝土的层裂现象进行了研究，得到了全场位移、应变等信息，在此基础上结合虚位移方法反演出材料不同本构方程的力学参数，极大促进了材料动态本构方程建立的发展。RIDDHIMAN[26]、ZHANG[27]等将DIC方法应用于SHPB实验，获得了陶瓷、岩石等典型脆性材料在动态拉伸及压缩条件下的应变场。谢倍欣等[28]以钢纤维混凝土的散斑SHPB试验为例，提出了一种基于DIC的试件应力应变时程曲线获取方法，避免了使用传统应变片处理数据时选择波形时间起点困难的问题，且可实现试件两端应力状态的实时评估。但另一方面，需合理设计光源位置、改进散斑和图像质量等方面，进一步提高测量精度。代树红等[29]利用DIC和数值模拟相结合的方法对层状岩石中裂纹的扩展规律进行了详细的研究与分析。韩秀会等[30]利用DIC结合高速摄影作为试验的观测手段，通过数字图像灰度相关性分析获得了冲击荷载作用下巴西圆盘煤样的冲击劈裂变形场演化规律，发现试件两端加载处由于应力集中出现了局部破碎区，如图6所示[30]，主裂纹从破碎区萌发并沿加载方向扩展，直至贯通到另一端，由于压碎区的存在使得通过巴西圆盘试验测得的煤岩抗拉伸强度低于实际值。章超等[31-32]利用SHPB结合DIC技术对泡沫铝在冲击载荷下的变形机理进行了分析，并指出材料中应力和变形不均匀是由于材料本身不均匀所引起的惯性效应(局部)和失稳(整体)造成的。DIC技术现已被广泛应用于SHPB实验，DIC技术为研究不同材料在动态破坏下的裂纹扩展、断裂方式行为等提供了测试手段，极大促进了断裂力学、动态力学等学科的发展。

(a)标示点6图像灰度相关性 (b)标示点7图像灰度相关性

(c)破坏时刻图像灰度相关性 (d)破坏时刻散斑图

关于DIC方法的位移测试精度国内外学者进行了大量研究，结果表明，影响DIC位移测量精度的因素主要包括散斑质量、搜素算法、亚像素插值方法、光学镜头畸变、子区位移模式等[33-36]，其中散斑质量对计算精度的影响尤为重要。散斑质量评价的标准应综合考虑系统误差和随机误差[37]，优质的散斑图案应具有各向同性、细节丰富、非周期性、良好对比度等特点。PAN等[38]验证了平均灰度梯度越大，散斑质量越好。俞海等[39]指出平均灰度2阶导数越低，对应散斑图的位移测量误差越小。在实际应用中应结合平均灰度梯度和平均灰度2阶导数两者，对散斑质量进行综合的有效评价。

3 结语

基于应变电测法的分离式霍普金森杆技术现已被广泛应用于工程材料在高应变率加载下的动态力学性能测试中，但随着科学技术的发展，人们对测试精度提出了更高的需求，更多关注于材料破坏的动态变形机理，此时传统的接触式应变电测法的弊端开始显现出来，如测量精度不高、无法观测材料在动态加载下的局部变形和细节特征。最近几年，DIC技术由于具备非接触式、测试结果精度高、抗干扰强、可视化程度高等优点，在断裂力学、动态力学等领域得到广泛应用。尽管基于数字图像相关方法的霍普金森压杆实验技术还存在一些有待改进的地方，但是为了获取更高精度的试验数据、更可观的试验过程应变场变化影像和更小尺寸试件的测试需求，霍普金森压杆实验技术结合数字图像相关方法仍是今后主流的研究方向，具有广阔的应用前景。