智能网联交通系统多层次映射关系建模

杨淇铭，唐进君，付 强，刘 佑

(1.中南大学 交通运输工程学院，长沙 410075；2.同济大学 交通运输工程学院，上海 201804)

近年来，人工智能、深度学习、大数据及5G等技术的快速发展，推动了交通系统领域的快速前进, 交通系统的发展目标逐渐由智能交通系统升级至智能网联交通系统。2017年9月，我国发布了首个V2X应用层标准《合作式智能运输系统 车用通信系统 应用层及应用层数据交互标准》(T/CSAE 53-2017)。2018年底，我国工信部正式规定5.905～5.925 GHz频段为智能网联汽车产业化专门应用的专用频段，并支持向5G标准的演进[1]。2019年9月，中共中央、国务院印发的《交通强国建设纲要》再次强调，要大力发展智慧交通，推动大数据、互联网、人工智能、区块链、超级计算等新技术与交通行业深度融合[2]。目前,有关智能网联交通技术及应用的研究已成为国内外学者的热点话题。缪立新、张洲、钱志鸿、余悦等[3-6]重点宏观阐述了智能网联技术的发展历程以及对未来的展望；陈敏、幽兰、刘新宇、高风、崔明阳等[7-11]则聚焦于智能网联汽车相关技术的发展现状、架构及前景；纪斌义等[12]阐述了基于V2X的智慧公路发展；钱宇清等[13]综述了智能网联技术支持下的城市智慧交叉口研究；刘玮等[14]研究了5G基站型路侧设备的技术方案与应用；卓福庆、俞天一、高书涛[15-17]对智能网联车辆在交叉口的通行方法展开了研究；范明星[18]设计了车路协同的路口智能决策系统；李林恒等[19]提出了基于安全势场理论的车辆换道模型；李云辉[20]研究了智能网联汽车的人机交互问题;Lian等[21]综述了智能交通系统和网联汽车产业中的大数据应用；Shi等[22]提出了智能网联交通系统中基于参与感知分类任务的多模型诱导网络；Sumalee等[23]展望了互联环境下的智能交通系统适应性态势；Borodin等[24]提出了协同运输规划的混合智能系统；Ma等[25]在道路通行能力和污染物排放方面分析了智能网联汽车对交通流的影响；Wang等[26]提出了用社会概率和资源有效(SPARE)协议来提高交付率和最小化网络资源的消耗；Wan等[27]提出一种适用于预定时交通信号场景下的速度推荐系统，以最小油耗作为目标函数调整车辆的驾驶行为，并通过微观仿真评估其应用影响；Li等[28]研究了智能网联的信号协同配时优化问题。

综上所述，目前国内外研究中关于智能网联交通系统整体组成元素(行人、车辆、道路、管控)之间相互影响作用关系的分析数学表达尚有欠缺。文中旨在从宏观角度分析智能网联交通系统发展现状下各子系统之间的相互作用关系，并通过建立数学模型分析作用关系间的影响。

1 智能网联交通系统多层次映射关系模型

基于系统多层次映射关系模型[29]，应用智能网联交通场景，分析智能网联交通系统中各子系统间相互影响程度关系及其对系统运行稳定性的影响。

1.1 系统多层次映射关系

从层次结构上看，智能网联交通系统可以从上至下划分成系统层、子系统层和系统元素层3个层次。根据逻辑关系，每个层次在系统运行时的外在表现和关注点都有所不同,如图1所示。

图1 智能网联交通系统多层次映射关系

对于智能网联交通系统而言，从评定系统运行状态角度看，底层的关注者主要是各交通出行者，其关注重点在于单次出行体验，关注底层具有具体性和实用性意义；中层的关注者主要是各出行服务提供的企业，其关注重点在于提供的服务是否适合当前交通场景、服务的质量如何，关注中层具有局部性和针对性意义；顶层的关注者主要是交通管理部门，其关注重点是路网的整体运行情况，关注顶层具有方向性和统筹意义。然而，随着系统规模和智能化程度加深，顶层交通管理者需要对各个子系统有清晰的认知，才能对中层的各个服务企业提出正确的改进方向和建议，为底层出行者提供更好的出行服务，提升出行者的出行体验。

1.2 智能网联交通系统子系统间关系

文中将智能网联交通系统分为智能移动终端(行人)、智能网联汽车(车辆)、智能网联道路(道路)以及交通管控设施(管控)4个子系统，子系统间关系可以分为“感知”(Sense)与“连接”(Connect)，其中，感知表示通过传感器、雷达等设备获取对应目标状态信息，“连接”表示通过统一标准的通信协议建立连接，并进行信息交互共享，虽然行人并不一定全部携带智能移动终端并授权终端定位，但其它智能网联子系统可以通过其感知设备获取行人信息。同理，智能网联交通系统内各子系统间是可以通过传感设备和通信设备进行广泛感知和连接，子系统间关系如图2所示。

注：图中有向线段表示各子系统间相互感知与连接图2 智能网联交通子系统间关系

1.3 系统动态分析模型

1.3.1 横向关系模型

1)横向影响关系。如图3所示，中层各子系统经过感知与连接，相互之间获取信息，做出相应响应，其横向关系(有向关系)如图3中所示。其中，aVR等表示子系统间的作用程度大小。

注：V为车辆子系统,R为道路子系统,P为行人子系统,C为管控子系统。图3 智能网联交通子系统间作用关系

2)子系统间作用关系。对于智能网联交通子系统，其相互之间影响程度可通过关系矩阵进行定义。两个子系统间的作用关系如图4所示。aij表示子系统i对子系统j的作用程度大小，aji则反之。

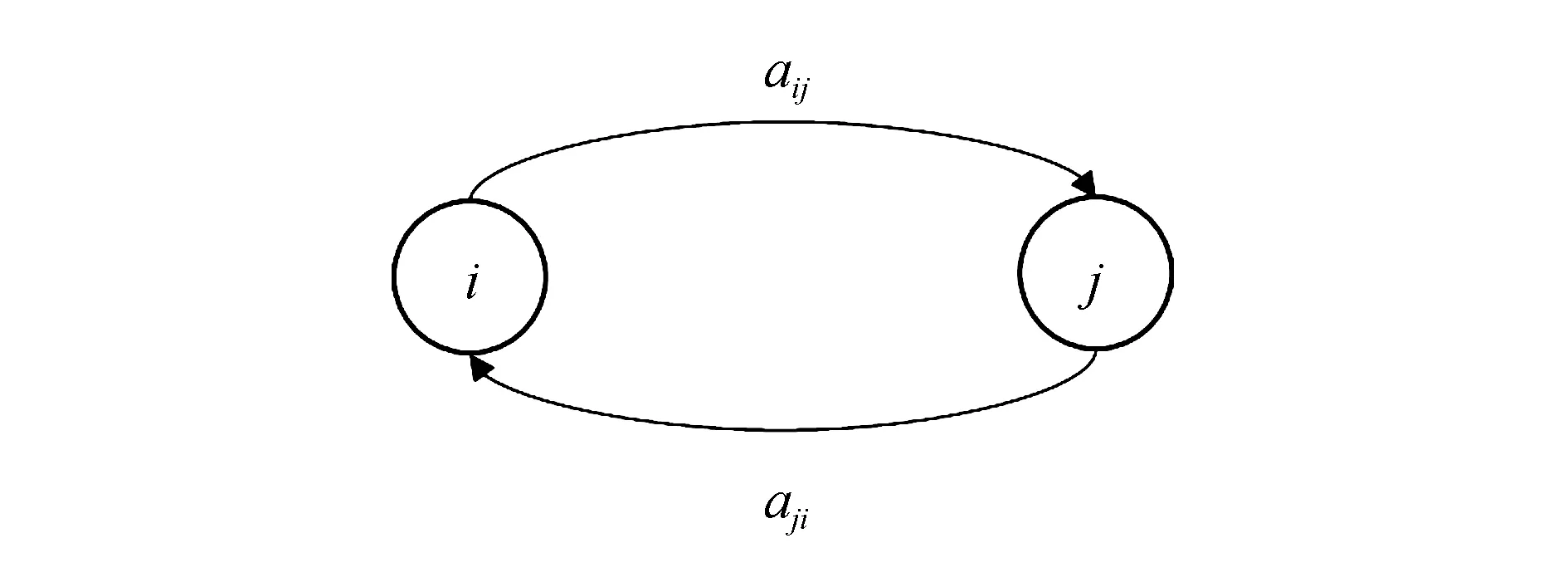
图4 子系统间的作用关系

子系统i对子系统j的影响程度可以通过子系统i的状态值(Xi)与子系统间i→j的作用程度(aij)的乘积进行定义，即Xi×aij，反之，子系统j对子系统i的作用为Xj×aji。根据交通系统运行特征可以发现，aji有时与aij并不相等，因此，表示子系统间相互作用关系的矩阵M为非对称矩阵。

关系矩阵M仅仅反映了子系统之间的直接作用关系，对于交通系统而言，行人、车辆在道路上的移动可以视作为“流”的概念。而对于一个有固定周期信号灯约束的交叉口，若以一个完整的信号灯周期来划分，由于行人、车辆到达的随机性，若影响按照信号灯周期划分，则一个周期内的行人、车辆、道路状态会对下一个周期的行人、车辆、道路状态有一定的延时影响。这在现实的交通场景中常表现为：交叉口排队的车辆在该方向的一个绿灯通行时长内无法全部通过，导致下一个周期内到达交叉口的车辆排队长度增加。假设总影响时间划分为t阶，因此，在t阶内对交叉口的总作用影响就包括了子系统内的直接作用、子系统间的间接作用以及延时反馈的振荡影响作用。假设对于某一智能网联交叉口，其人、车、路、管控的初始状态值为(X1,X2,X3,X4)，其一个周期作用的影响传播反馈系数为τ(0<τ<1)，则t阶作用后的子系统状态值就变成(X1,X2,X3,X4)×M(τ)×τt-1，因此，在总作用时间内子系统的状态向量为

G=(X1,X2,X3,X4)·M+(X1,X2,X3,X4)·

M2τ+…+(X1,X2,X3,X4)·Mtτt-1=

(1)

这里将

(2)

称为网络N的多重反馈影响关系矩阵，与仅仅包含直接作用关系的M相比，A具有更丰富、更全面的作用关系，也更加符合现实交通情况。

对于考虑了网络传播反馈因素的影响关系矩阵A，实际计算中若作用时间t很长，将包含大量求和计算，由于反馈系数τ在高阶时将变成很小的数，在现实中表现为多个信号周期前的行人、车流情况对新输入的行人、车流的影响可以忽略，因此，可以对A求极限。

对于

(3)

有

(4)

即

(5)

所以

(6)

所以

(7)

式中：E为单位矩阵。

当t很大时有

(8)

因此可以表示为

A=M(E-τM)-1

(9)

且有

(10)

1.3.2 纵向关系模型

系统状态波动变化往往是从子系统内某一元素出现扰动因素而导致，元素的扰动会导致子系统状态发生变化，进而影响整个系统的稳定性，纵向各层次的逻辑关系如图5所示。

图5 系统纵向作用逻辑关系

根据图5，对于子系统内的元素扰动可以用扰动值X来定义，子系统状态可以用R来标定，而整个系统的稳定性可以通过S来进行评价。

由于智能网联交通系统是人、车、路协同的系统，其某一子系统内的扰动可以通过其他子系统的快速协同作用来保证整个交通系统迅速恢复稳定运行状态，因此,对于协同的子系统而言，其“扰动值”在某种程度上也可以理解成为协同动作值。对于整个系统，设初始扰动值X(0)=(X1,X2,X3,X4)，由于子系统间有延时的相互影响作用关系，因此,整个系统在t阶作用时间内、在作用反馈系数τ的影响下，存在以下关系

X(t)-X(0)=AX(0)

(11)

即

X(t)-X(0)=(A+E)X(0)

(12)

式中：E为单位矩阵。

X(t)表示子系统在反馈影响矩阵作用下经过t时间后的各子系统内元素状态属性值，定义多重反馈作用后的子系统响应向量为R=(R1,R2,R3,R4)。

由上述公式可得，对于第i个子系统的响应量Ri有

Ri=∑j[Aij+δij]Xj

(13)

δ为克罗内克函数，当i=j时，δ=1，当i≠j时，δ=0。

而A=M(E-τM)-1

所以

Ri=∑j[Mij(E-τMij)-1+δij]Xj

(14)

对于整个系统，其稳定性S可以通过

(15)

进行评价，其中ωi是第i个子系统对整个系统的影响权重，且满足

∑iωi=1

(16)

S值越小，说明整个系统越稳定，理想情况下S=0，即整个智能网联交通系统所有的运行都是流畅的，但由于信号灯的约束，各个方向车流、人流存在冲突等因素，这个目标几乎不可能实现。因此在本模型中，只要应用协同后计算得到的稳定性指标S值相较于无协同的情况变小即可。

根据上述公式，智能网联交通系统子系统间的协同作用关系模型如图6所示。

图6 智能网联交通系统多层次映射关系模型稳定性计算流程

1.4 智能网联交通系统稳定性指标评价体系

对于智能网联交通系统而言，由于其系统目标在于实现安全、高效、舒适、精确的出行服务，因此，可以通过以下8项指标对系统的稳定性、运行情况进行评价。

1)道路交通事故率：是指一定时期内某一特定范围内事故发生数量与该范围内的人口数、车辆数、运行里程之间的比例关系，是用于安全方面的评价，在评估车辆主动安全技术时可以纳入考虑。随着智能网联交通系统技术发展成熟度的提高、应用范围的增大，道路交通事故率将呈现明显下降趋势。

2)交通事故严重程度：是指若不幸发生交通事故，事故造成的人员伤亡情况和财产损失情况，可用于安全方面的评价，在评估车辆主动安全技术时考虑。由于前向碰撞预警等车辆主动安全技术的发展，交通事故严重程度将大幅降低。

3)路网通行能力：是指在一定的交通状态下，一定时间(日、小时)内，道路网某区域内所能负担的交通能力，是效率方面的评价指标，以每小时通过的车辆数为衡量标准，在评估智能网联技术对交通流的促进作用时考虑。智能网联交通系统通过人、车、路、管控协同联动等将大幅度提高城市路网通行能力。

4)车辆出行行程时间：是指单辆车从其始发地到目的地的整个出行过程所用时间，主要考虑与自由流下的期望时间相比，是效率方面的评价指标，在评估智能网联技术对车辆出行促进作用时考虑。智能网联程度越高，车辆出行越顺畅，出行行程时间也就越接近自由流下的期望时间。

5)乘车舒适度：是指城市居民在乘车出行过程中，由于车辆加减速、变道等操作行为而在生理、心理方面对出行的反应指标，用于舒适度方面评价，在评估智能网联技术对乘车人出行体验的提升作用时考虑。在智能网联交通系统中，各交通要素之间能够通过多维感知技术将车间距时刻保持在安全范围，从而保证较高的乘车舒适度。

6)行走便捷性：是指城市居民在步行出行过程中，根据人行道状况、目的地路径选择、过街需求满足情况等城市道路建设情况产生的心理满意程度，用于舒适度方面评价，在评估智能网联技术对非机动车和行人出行的体验提升作用时考虑。智能网联交通系统通过行人与车辆之间的感知保证行人行走的安全性。同时，道路智能化程度越高，高精度实时定位技术为行人提供的行走指引也越明确，行人的行走便捷性也越高。

7)交通感知精确度：是指交通管控设备对车辆、行人的感知以及与其他通信设备连接的稳定程度，在评价智能网联交通管控设备的感知准确度时考虑。在智能网联场景下，如果不能保证高可靠性、精确的感知和连接，那么所有后续的控制、决策都将丧失方向，缺少针对性，进而丧失了智能网联交通系统的先进技术优势。

8)交通管控有效度：是指用于智能网联交通系统的交通管控设备在感知到行人、车辆特征后，决策实施的有针对性的管控措施及实施效果，用于评估交通管控设备的有效性。在智能网联交通系统中，交通管控设备是维持系统稳定性的重要一环，交通管控设备在日常运行中的稳定决策表现反映了智能网联交通系统的技术进展程度。

2 模拟场景模型验证

下面用一个协同联动的模拟场景对上述模型进行验证。考虑一个城市中的T型交叉口及其附近路段，假设该交叉口为完全智能网联交叉口，车辆均为智能网联汽车，交叉口附近布置有精度较高的行人检测设备和通信设备，道路均匀布置RSU，且能够将交叉口信息稳定传输给附近车辆。利用SUMO仿真软件建立仿真场景，设定相关参数，多次运行仿真，调整人、车、路、管控的参数，根据仿真结果文件来标定各子系统对整个系统稳定性的影响权重，最终得到行人、车辆、道路、管控子系统的影响权重向量为ω=[0.19 0.23 0.34 0.24]。

2.1 基于车速推荐的智能网联交叉口协同控制

在某信号灯相位黄灯时间的第2 s，路侧单元对在人行横道边等待的行人进行感知与识别，通过计算得到供行人安全通行的接下来绿灯相位时长，并相应地调整车道的绿灯相位时长。接下来到达交叉口车辆根据与RSU及信号灯的连接，获得目标车道在交叉口处的可供通行最小时长和最大时长，据此计算推荐车速。当推荐车速不超过限速范围时，车辆执行车速推荐策略，以不影响乘车人舒适度的方式调整自身速度，以达到不停车通过交叉口目的；当推荐车速超过路段限速范围时，车辆调整至最经济节能的驾驶模式行驶至交叉口停车线处等待绿灯通行，具体流程如图7所示。

图7 基于车速推荐的智能网联交叉口协同控制流程

2.2 系统评价指标确定

在应用前文所述模型时，对各个子系统需要有具体定性的评价指标予以标定其影响作用的“正负值”：对行人子系统，在交叉口处最应关注的是过街行人数量；对车辆子系统，在交叉口处对整个系统运行影响最大的是排队车辆数；对道路子系统，可以用路面状况和路侧单元感知准确度、计算复杂度来评价；对管控子系统，可以用管控措施的有效度来进行评价。状态评价指标如表1所示。

表1 智能网联交叉口各子系统状态评价指标

2.3 子系统间的影响关系矩阵

各子系统间影响关系有正反馈(用“+”表示)和负反馈(用“-”表示)。正反馈表示一个子系统评价指标的提高会提升另一个子系统评价指标，如过街行人增多会增加交叉口平均排队车辆数；负反馈表示一个子系统指标的提升会降低另外一个子系统的评价指标，如车辆增多会降低道路路面状况良好程度。对于影响程度的确定，文中定义影响程度分为4级，±3表示影响非常强烈，±2表示影响强烈，±1表示有一定影响，0表示影响可以忽略，根据笔者个人判断建立了影响关系矩阵，结合一致性检验方法最终确定了子系统间影响关系值矩阵，最终矩阵的一致性检验值CR=0.012。智能网联交通子系统间影响关系如表2所示。

表2 智能网联交通子系统间影响关系

子系统间的影响关系矩阵为

在文中的研究中，设定多重反馈系数τ=0.4，根据A=M(E-τM)-1可以求得多重反馈作用下智能网联交叉口子系统影响关系矩阵为

2.4 智能网联交叉口应对扰动的协同响应情况

在正常情况下，包含行人子系统、车辆子系统、道路子系统、管控子系统的智能网联交叉口处于一个相对稳定状态，表现为行人能够安全过街、车辆能够顺畅通过交叉口、路面状况良好以及信号灯等智能交通设备正常运作，但由于交通流的不确定性以及城市规划活动等原因，交通系统组成元素的状态突变将会影响到相应子系统的稳定状态，进而影响到整个系统的稳定性。智能网联交通系统通过人、车、路、管控的协同联动，能够很好地处理交通出行场景中的元素扰动情况。

1)初始条件。外部环境良好、路段所有车辆状态良好、行人行走速度正常，交通基础设施正常运转。

2)行人子系统发生扰动。当东西方向过街行人人流量增加至300人·h-1时，定义行人子系统扰动值为1，即在不考虑协同的情况下，系统状态向量X=(1,0,0,0)，动态响应向量R=(-0.93，-1.40,1.21,0.82),稳定性评价指标S=0.40；应用协同联动措施后，整个系统的状态向量为X=(0.8,0.1,-0.1,0.2)，动态响应向量为R=(-0.73,-1.16,0.93,0.73)，此时系统稳定性评价指标下降为S=0.36。

3)车辆子系统发生扰动。当南北方向车流量各增加200 veh·h-1时，定义车辆子系统扰动值为1，系统状态向量X=(0,1,0,0)，动态响应向量R=(-1.52,-1.94,1.52,1.40)，稳定性评价指标S=0.68；应用协同联动措施后，整个系统的联动状态向量为X=(0.1,0.8,0.2,-0.3)，动态响应向量为R=(-1.48,-1.85,1.56,1.23)，此时系统稳定性评价指标下降为S=0.60。

4)道路子系统发生扰动。南北方向道路限速降低至60 km·h-1时，定义道路子系统扰动值为-1，系统状态向量X=(0,0,-1,0)，动态响应向量R=(-1.65,1.52,1.36,1.21)，稳定性评价指标S=0.60；应用协同联动措施后，整个系统的联动状态向量为X=(0.2,-0.2,-0.8,0.3)，动态响应向量为R=(-0.71,-0.65,0.53,0.58)，此时系统稳定性评价指标下降为S=0.28。

5)管控子系统发生扰动。当某处发生交通事故需要管制一定路段时，定义管控子系统扰动值为-1，系统状态向量X=(0,0,0,-1)，动态响应向量R=(-1.65,-1.52,1.65,0.93)，稳定性评价指标S=0.46；应用协同联动措施后，整个系统的联动状态向量为X=(0.1,-0.1,-0.1,-0.8)，动态响应向量为R=(-1.43,-1.32,1.43,0.81)，此时系统稳定性评价指标下降为S=0.40。

根据评价指标的对比可以看出，文中应用的考虑多重反馈的智能网联交通系统多层次映射关系模型与理论结果相一致，该模型在实际交通场景中有一定的应用参考价值。

3 结 语

文中所建立的智能网联交通系统多层次映射关系模型能够协助评估智能网联交通发展阶段，使发展智能网联交通技术有更清晰明确的目标，协助分析智能网联交通系统之间各元素的相互作用关系。其不足之处有以下两方面：

1)模型中子系统间相互影响程度的确定未得到大量数据支撑；

2)考虑的是完全智能网联环境，对于在城市交通中的实际应用还有一定距离。