日本新干线隧道缓冲结构技术
喻 渝 景雪蕾 冯春来 梅元贵
(1.中铁二院工程集团有限责任公司, 成都 610031;2.兰州交通大学甘肃省轨道交通力学应用工程实验室, 兰州 730070)
当高速列车驶入隧道时会在车头前形成压缩波,该压缩波以声速传播到隧道出口,其中一部分压缩波辐射出隧道外形成持续时间短的脉冲波,通常称为“微气压波”。微气压波含有大量频率在20 Hz以下的低频次声波,而频率在20 Hz以上部分的微气压波则可能会产生音爆,在隧道出口形成“轰鸣声”,影响隧道周围建筑和居民,造成环境问题[1]。列车驶入隧道时产生的微气压波大小与出口端压缩波最大梯度成正比[2-3],压缩波最大梯度与列车速度的3次方成正比[4]。由于日本新干线隧道内净空采用64 m2的小断面,1974年在三阳新干线运行期间首次发现了微气压波问题[5-6],为此日本进行了大量系统的研究工作,通过采用在隧道洞口设置缓冲结构的方法,较大幅度地减缓了微气压波的影响。日本新干线早期设置的隧道缓冲结构长度一般为12~17 m,随着日本新干线的提速,微气压波现象变得更加剧烈,为此持续设置了长度10~30 m的不同型式微气压波缓冲结构[7-9]。在设计速度505 km/h的中央新干线山梨磁浮试验线中设置了长达200 m的隧道开孔型缓冲结构。目前,日本学者正在围绕时速360 km/h及更高速度的隧道缓冲结构进行研究。考虑到在世界范围内日本有关缓冲结构的研究和工程应用较为系统,本文重点调查分析了日本新干线已建成的部分隧道缓冲结构,以及360 km/h的隧道缓冲结构气动效应深化研究成果,期望为我国400 km/h及以上速度的隧道缓冲结构设计和施工提供参考。
1 既有隧道缓冲结构型式
目前,日本新干线隧道缓冲结构可分为无开孔缓冲结构和开孔型缓冲结构两类。按照隧道缓冲结构断面面积变化特征,也可将缓冲结构形状分为等截面型和扩大截面型两大类[10]。开孔型缓冲结构主要有顶部、侧部开孔及狭缝型开孔等类型。
1.1 缓冲结构基本结构型式
日本新干线既有缓冲结构的一些基本结构型式如图1所示,包括喇叭形扩大断面开孔型、等截面扩大断面开孔型、扩大断面无开孔型、既有结构延长型4种类型。
(1)如图1(a)所示,目前使用的扩大断面开孔型缓冲结构的横截面面积与隧道横截面面积之比在1.4~1.5之间,且沿侧壁一侧或两侧都有开孔。日本列车以250~320 km/h运行时,缓冲结构长80 m,当速度增加到350 km/h或更高时,所需的缓冲结构长度可能将超过100 m[11-13],如图1(b)所示。
(2)在洞外某些特殊环境条件限制下,研究提出了长度较短的无开孔等截面扩大断面型的缓冲结构,可解决开孔布置困难的情形,缓冲结构的情况如图1(c)所示。
(3)图1(d)是一种在既有缓冲结构基础上延长长度的开孔型缓冲结构,以解决既有线路上提速后恶化的微气压波问题。

图1 缓冲结构的基本型式图
1.2 缓冲结构中开孔的布置方式
开孔型缓冲结构可较大幅度地降低列车驶入隧道带来压缩波的最大压力梯度,是一种非常有效的工程措施。不同开孔型式的缓冲结构如图2所示,具体包括:两侧开孔、等间距开孔、非等间距开孔、非均匀尺寸开孔和混合型非等间距开孔5种类型缓冲结构。
(1)图2(a)和图2(b)分别为等间距布置“正置型”矩形开孔的两种缓冲结构型式。缓冲结构长度分别为10 m和49 m,如图2(b)所示的结构设置9个开孔[14]。
(2)图2(c)和图2(d)分别为非等间距布置矩形开孔的两种缓冲结构型式。图2(c)结构特点是在缓冲结构前端布置第一个开孔,而后间隔两个开孔的尺寸后再布置一定数量的开孔。
(3)图2(e)为“反置型”的“狭长”型的矩形开孔和“方形”开孔两种混合型的非等间距开孔缓冲结构。

图2 缓冲结构的开孔型式图
以上缓冲结构的开孔大小、开孔位置和是否均匀布置开孔等参数均需根据列车速度、隧道长度等边界条件进行具体研究才能得出。
1.3 高速磁浮隧道缓冲结构
为消除505 km/h速度高速磁浮隧道微气压波危害,日本中央新干线的山梨试验线设置了长大开孔型缓冲结构,其最长缓冲结构已达200 m,隧道净空面积74 m2,在缓冲结构前端布置了大量开孔[15],其效果满足隧道长度不超过45 km的微气压波控制值。“方型”和“拱型”两种断面型式的开孔缓冲结构如图3所示。方型缓冲结构截面积比隧道截面积大,其顶部布有直径为10 cm的开孔。拱型缓冲结构截面积与隧道截面积相同,在缓冲结构的前端开孔率为10%,后端的开孔率为0.5%。

图3 高速磁浮隧道缓冲结构断面型式图
2 基于更高速度条件下的缓冲结构深化研究
随着新干线提出提高运营速度的要求,日本相关单位和学者利用模型试验及数值仿真分析手段,针对无开孔及开孔型两种缓冲结构,开展了基于 360 km/h速度的缓冲结构的深化研究。
2.1 无开孔缓冲结构深化研究
2.1.1 等截面扩大断面无开孔型缓冲结构最优断面积比
针对更高速度条件下的等截面扩大无开孔型缓冲结构,Saito S[15]等开展了动模型试验及数值仿真,对该结构的微气压波峰值特征及最优断面积比进行了研究。
无开孔扩大断面比为2.4条件下,采用模型比为1/102旋成体动模型试验得出的压缩波压力和压力梯度的时间历程曲线特征图如图4所示[15],试验相对应的列车车头长10 m,缓冲结构长39 m。从图4可以看出,无开孔缓冲结构压力波形曲线较为复杂,并且无开孔缓冲结构的压力波形有3个峰值。
采用数值计算方法,缓冲结构断面面积和隧道断面面积之比对压缩波压力梯度3个峰值最大值的影响结果如图5所示。纵轴表示带有缓冲结构的压力梯度比与无缓冲结构的压力梯度之比。随着缓冲结构截面积比的增加,第一个峰值减小,而第二个和第三个峰值增加。图5中3个压力梯度的峰值交点给出了缓冲结构断面面积和隧道断面面积之比的最佳值,最佳值约为2.6。
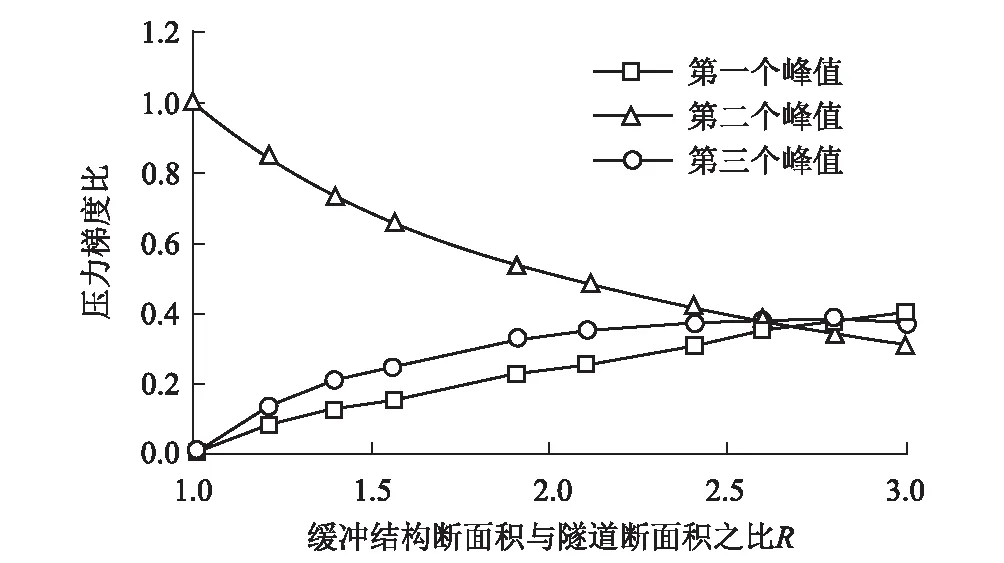
图5 每个压力梯度峰值的最大压力梯度的变化特征图
最优截面积比为2.6无开孔等截面缓冲结构和既有开孔缓冲结构(R=1.4)间的最大压力梯度比的比较如图6所示。在一定的缓冲结构长度下,无开孔缓冲结构的最大压力梯度最小。在这种情况下,最优的缓冲结构lh/d为1.8的最小压力梯度比为0.37,而开孔缓冲结构在lh/d为3时具有与无开孔缓冲结构相同的最小压力梯度比值。要达到最小压力梯度比0.37,无开孔缓冲结构可比开孔缓冲结构短40%。由此可知,扩大断面面积可有效减短缓冲结构长度;同时,由于无开孔缓冲结构不需要设置开孔,建造相对简单。
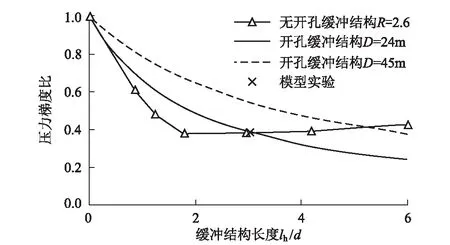
图6 有无开孔型缓冲结构结构的最大压力梯度的比较图
2.1.2 等截面二次扩大断面无开孔型缓冲结构断面积最优比值
考虑既有线提速后的缓冲结构改造问题,斉藤実俊、福田傑[16]等采取数值仿真分析手段,对等截面二次扩大断面无开孔型缓冲结构的断面积最优比值进行了深化研究。
二次扩大断面无开孔型缓冲结构的示意如图7所示,压缩波PE表示列车头部进入缓冲结构入口E时产生的压缩波,当列车车头通过J1交叉口时,会产生压缩波PJT1和向缓冲结构进口端反射的膨胀波PJH1。当列车车头通过隧道端J2时,会产生另外两个压缩波PJT2和膨胀波PJH2。图7中,接续隧道的第一个扩大断面面积和隧道断面面积之比为1.4[16]。运用数值计算方法,在360 km/h速度条件下不同的截面比(第二个扩大断面面积和隧道断面面积之比)对上述5种压力波压力梯度的影响规律如图8所示,图8中纵轴的压力梯度比是无缓冲结构时与压力梯度最大值的比。从图8可以看出,当第一个扩大断面面积与隧道断面之比为1.4时,第二个扩大断面面积和隧道断面面积之比为3.9,可最大程度减小压缩波的最大梯度值。
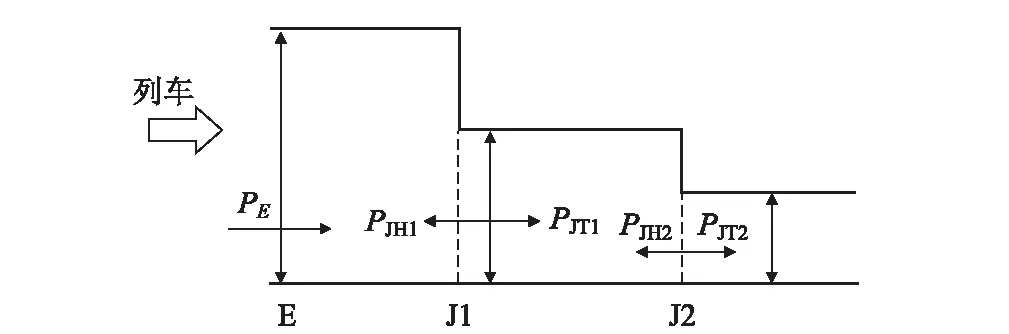
图7 等截面二次扩大断面无开孔型缓冲结构示意图
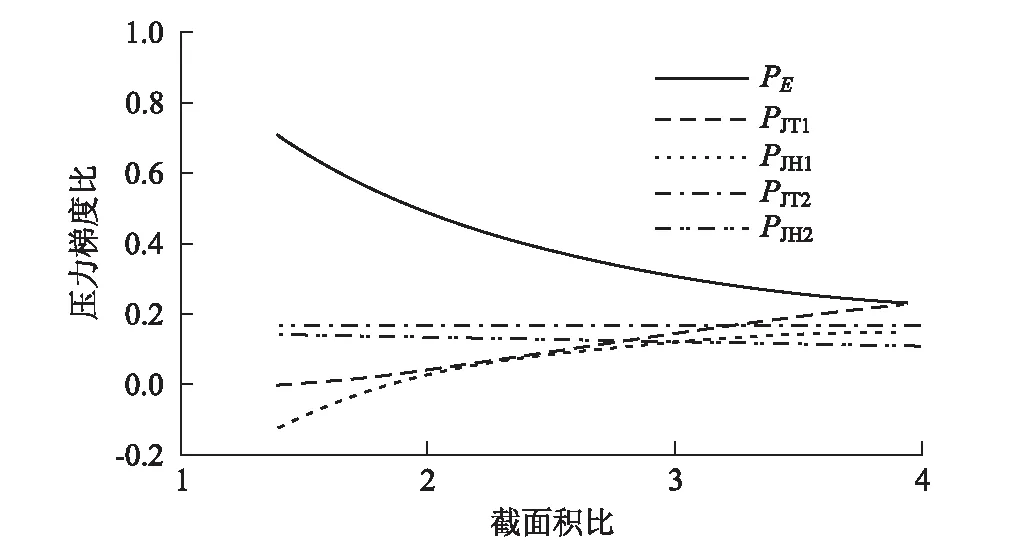
图8 隧道中压缩波压力梯度比的计算结果图
2.2 开孔型缓冲结构深化研究
2.2.1 开孔侧向的影响
既有隧道缓冲结构开孔特征是在缓冲结构的两侧分布着两个等间距的开孔,称为“两侧开孔”。考虑双线隧道,从列车驶入隧道的方向观察,将靠近列车一侧的开孔称为“近侧开孔”,远离列车侧的开孔称为“远侧开孔”。
栗田健[17]等针对“两侧开孔”与“近侧封闭、远侧开孔”两种开孔方式进行了数值仿真对比分析。
当缓冲结构断面面积与隧道断面之比为1.4时,采用数值计算方法,可得到的缓冲结构两侧开孔和近车侧开孔封闭、保持远侧开孔两种情况的的压力梯度时间历程曲线如图9所示[17]。从图9可以看出,设有两侧开孔的缓冲结构压力梯度的波形具有尖锐的峰值,而对于只在远侧开孔的缓冲结构,峰值会降低,并且压力梯度减小,减缓微气压波效果更为明显。
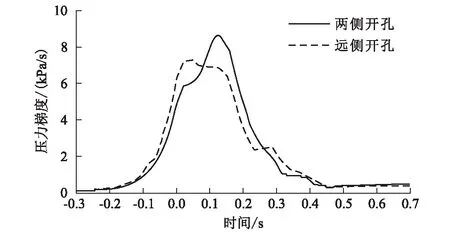
图9 缓冲结构开孔设定后的压力梯度图
2.2.2 等截面扩大断面缓冲结构开孔高度的影响
针对等截面扩大断面开孔型缓冲结构开孔高度的最优取值问题,宮地徳蔵[18]等利用动模型试验开展了深化研究。
等截面扩大断面开孔型缓冲结构开孔布置示意如图10所示。采用模型比为1/127旋成体动模型试验得出的开孔扩大断面比1.44条件下的开孔高度h和压力梯度比的关系曲线图如图11所示[18]。其中,列车速度360 km/h,车头长15 m。从图10可以看出,有明显的最佳的开孔高度。当缓冲结构30 m时,压力梯度比值的最小值为0.468,对应的开孔高度比为0.331。当缓冲结构50 m时,压力梯度比值的最小值为0.360,对应的开孔高度比为0.266。
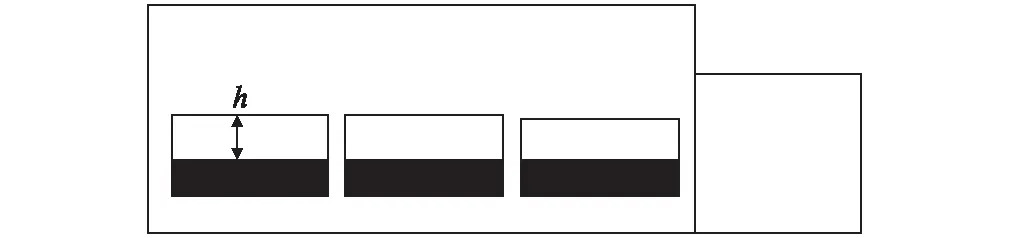
图10 等截面扩大断面开孔布置示意图
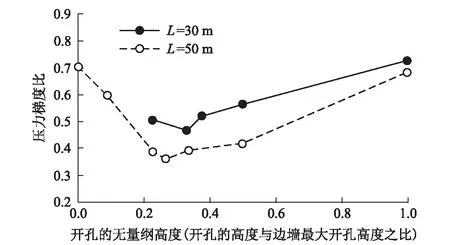
图11 开孔高度h和压力梯度比之间的关系图
当改变开孔高度时压力梯度波形的变化曲线图如图12所示。从图12可以看出,若开孔高度大于最佳开孔高度,即开孔过大,压力梯度波形向右上方升。如果开孔高度小于最佳开孔高度,即开孔过小,压力梯度波形向左上方升。当开孔高度h最佳时,压力梯度波形的两个峰几乎平齐。
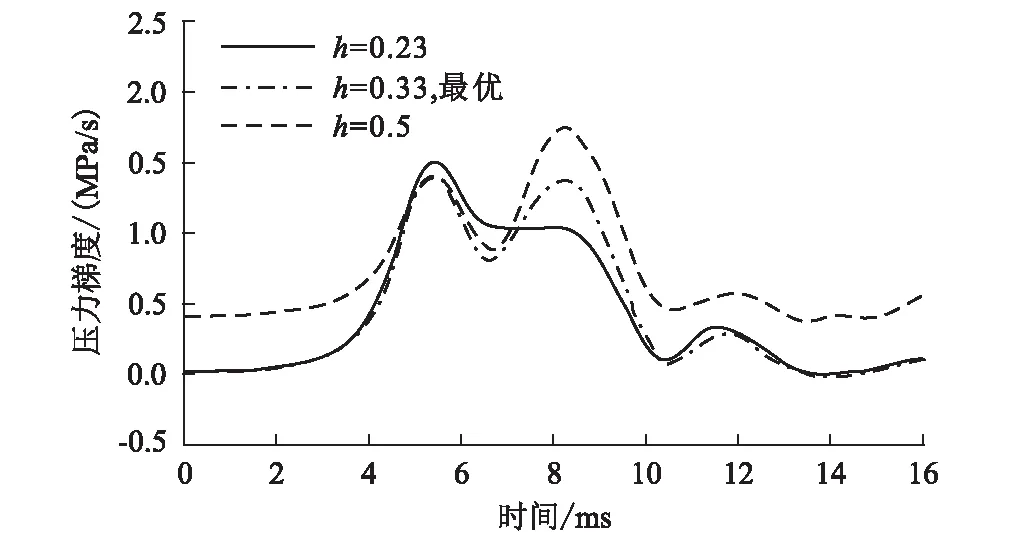
图12 当改变开孔高度时压力梯度波形的变化图
2.2.3 喇叭型缓冲结构开孔高度的影响
对于喇叭型缓冲结构,如何通过调整开孔高度实现微气压波的减弱,大久保秀彦、宮地徳蔵、福田傑[19]等通过动模型试验进行了深化研究。
喇叭型缓冲结构的示意如图13所示,其侧面设置了等间隔的开孔,缓冲结构的截面形状为正方形,且沿着开孔方向扩张,与隧道相连处截面积比为1.27,缓冲结构开孔处截面积比为2.5,在对称轴处设有开孔(高20 mm×宽24 mm),通过在中央安装封板来改变开孔高度h,h=0 mm时完全关闭,h=10 mm时完全打开,调节范围为2.5 mm≤h≤7.0 mm。采用模型比为1/127旋成体动模型试验得出的喇叭型断面比1.44条件下的压缩波压力梯度的时间历程曲线特征图如图14所示[20],对应列车速度360 km/h,车头长度15 m。从图14可以看出,当开孔高度h=0 mm时,压力梯度的波形在上半部具有1个高峰,在下半部具有1个低峰。当开孔高度h=2.5 mm时,上半部波形在上半部具有较低的峰值,在下半部具有的峰与下半部分的峰对齐,从而抑制了压力梯度的增加。因此,通过改变开孔高度h可以有效的改善喇叭型缓冲结构对微气压波的缓冲效果。
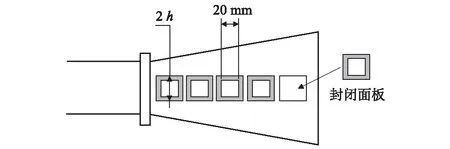
图13 喇叭型缓冲结构示意图
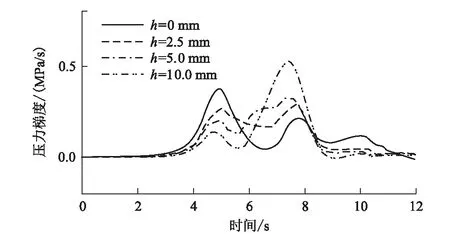
图14 缓冲结构长度lh=50 m时的压力梯度波形图
压力梯度比与缓冲结构长度lh之间的关系如图15所示,R为缓冲结构的断面面积与隧道断面面积之比。从图15可以看出,当开孔高度h=0 mm时(即无开孔),喇叭型缓冲结构长度为30 m和50 m处,压力梯度比大于断面比为2.5倍的缓冲结构。当优化开孔高度h时,压力梯度比小于断面比为2.5倍的缓冲结构。因此,通过将喇叭型缓冲结构与调整开孔高度的优化相结合可实现更优的微气压波的减小效果。
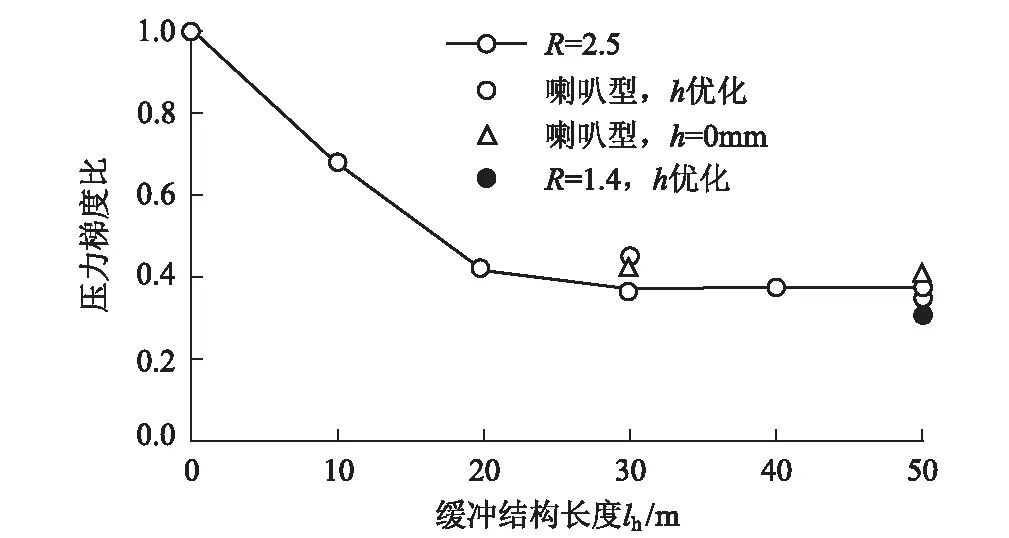
图15 压力梯度比与缓冲结构长度lh之比图
3 结论
缓冲结构是有效防治高速铁路隧道微气压波的工程措施。本文通过调研日本新干线既有隧道缓冲结构的工程应用和更高速度条件下的缓冲结构气动研究成果,可得到以下结论:
(1)目前新干线工程设置的既有隧道结构多为开孔型结构,开孔类型可分为等间距开孔和不等间距开孔。等截面开孔型缓冲结构易于延长,利于既有线缓冲结构的改造,适用于既有线提速下的隧道洞口微气压波控制。
(2)更高速度条件下的缓冲结构深化研究表明:无开孔型等截面扩大断面缓冲结构具有最优断面比取值;扩大缓冲结构的断面面积可有效减短缓冲结构长度;开孔型缓冲结构可采用较小的缓冲结构断面面积,但是开孔大小、个数、布置位置和开孔高度等参数及排列组合对降低压缩波梯度有重要影响,需要结合具体工程分析才能确定最佳方案。
从本文调研结果来看,对于我国400 km/h及更高速度的高速铁路隧道洞口缓冲结构宜采用等截面扩大开孔型缓冲结构。

