二阶微分方程系统求解极值映射不动点问题

王 莉，陈星旭，孙菊贺，杨 峥

(1.沈阳航空航天大学 理学院，沈阳 110136；2.辽宁省实验学校 数学教研组，沈阳 110031)

本文将研究极值映射不动点问题，即求解v*∈K使得

v*∈Argmin{Φ(v*,w)|w∈Ω}

(1)

这里Φ是定义在内积空间Rn×Rn上的极值映射，Ω⊂Rn是非空闭凸集合。假设Φ(v,·)关于第一元v是凸函数；对任意的v∈Ω，都有集值映射w(v)≡Argmin{Φ(v,w)|w∈Ω}，且原始问题(1)的解集Ω*={v*∈Ω|v*∈w(v*)}⊂Ω是非空的。

对于问题(1)的解应满足不等式

Φ(v*,v*)≤Φ(v*,w),∀w∈Ω

(2)

显然，不等式(2)是极值映射不动点问题(1)的等价定义。

Antipin[1-3]提出极值映射的不动点问题(1)，并指出该问题是不同类型、不同领域问题的一般表示，同时指出鞍点问题、具有纳什均衡的n人博弈问题、逆优化问题、变分不等式问题、不动点求解问题等都可以转化为极值映射不动点问题(1)。Antipin[1]研究了极值映射不动点问题的邻近方法。Antipin[2]研究了极值映射不动点问题的一阶微分方程方法。Antipin[3]首先研究了优化问题的一阶微分方程方法，进而提出了鞍点问题的具有控制过程的一阶微分方程方法，最后研究了极值映射不动点问题的具有控制过程的一阶微分方程方法。Wang等[4]研究了具有不等式约束的极值映射不动点问题的增广拉格朗日方法。Antipin[5]研究了一类优化问题的二阶微分方程方法。Wang等[6]运用二阶微分方程系统求解了具有不等式约束的极值映射问题。

值得指出的是，Antipin等学者的微分方程方法与Zhou等[7]、Jin等[8]与Zhou等[9]所使用的微分方程方法求解变分不等式和互补问题是完全不同的；不仅如此，与Gao等[10]、He等[11]与Liao等[12]的神经网络方法求解优化方面问题也不同。以往的方法是把原始问题转化成光滑的无约束优化问题，运用该优化问题的负梯度来构造微分方程系统，并构造李亚普诺夫函数来证明微分方程系统的稳定性。而Antipin等学者直接利用非光滑的投影算子构成的方程组建立微分方程系统，运用投影定理及内积与范数的运算得到微分方程系统的轨迹收敛性。但是Antipin等学者的工作却没有得到足够的重视，Facchinei等[13]的专著几乎收录了变分不等式和互补问题的所有重要成果，但却没有记录该方法。王莉[14]关注了Antipin等学者的工作，并进一步用该思想解决了具有循环单调映射的变分不等式的微分方程方法。

在以上研究结果的基础上，本文研究极值映射不动点(1)的二阶微分方程系统。在第一部分将介绍本文将要用到的预备知识如投影算子、对称函数和反对称函数的一系列性质；在第二部分运用函数Φ(v,w)及投影算子的性质，建立二阶微分方程系统，并证明二阶微分方程系统轨迹的聚点就是极值映射不动点问题的解；最后给出具体的算例说明二阶微分方程系统求解极值映射不动点问题的有效性。

1 预备知识

为了建立二阶微分方程系统，首先介绍关于对称函数与反对称函数的性质。

定义1[3]满足式(3)的函数称为对称函数，满足式(4)的函数称为反对称函数。

Φ(w,v)-Φ(v,w)=0,∀v∈Ω,∀w∈Ω

(3)

Φ(w,v)+Φ(v,w)=0,∀v∈Ω,∀w∈Ω

(4)

Antipin[3]给出函数Φ(v,w)转置的定义，即ΦT(v,w)=Φ(w,v)。则对称函数和反对称函数的转置可以分别表示为

Φ(v,w)=ΦT(w,v),∀v∈Ω,∀w∈Ω

(5)

Φ(v,w)=-ΦT(w,v)，∀v∈Ω,∀w∈Ω

(6)

因此函数Φ(v,w)可以做如下分解

Φ(v,w)=S(v,w)+K(v,w)

(7)

其中函数S(v,w)和K(v,w)定义如下

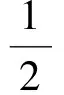
(8)

则容易验证S(v,w)为对称函数，K(v,w)为反对称函数。

Antipin[3]证明了对称函数和反对称函数的性质如下

性质1[3]对称函数S(v,w)在Ω×Ω的对角线上的关于第一元v和第二元w的偏导数相等，即

∇Sv(v,v)=∇Sw(v,v),∀v∈Ω

(9)

更进一步，Antipin[3]讨论了当函数S(v,w)中v=w时可以得到

2∇Sw(v,w)|v=w=∇S(v,v),∀v∈Ω

(10)

定义2[3]函数S(v,w)称为伪对称函数，如果存在函数P(v)使得

∇P(v)=2∇wS(v,w)|v=w，∀v∈Ω

(11)

显然，对称函数一定是伪对称函数。在这种情况下

∇P(v)=∇S(v,v)，∀v∈Ω

(12)

Antipin[3]给出了定义2中的函数P(v)，梯度∇P(v)满足下面的Lipschitz条件，其Lipschitz常数为Lp如下

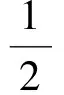
(13)

梯度∇P(v)满足单调性条件

〈∇P(v+h)-∇P(v),h〉≥0，∀v∈Ω

(14)

由反函数的定义式(4)，如果v=w，可以得到K(v,v)=-K(v,v)，即K(v,v)=0对于所有的v∈Ω。这就意味着反对称函数K(v,w)在Ω×Ω对角线上的元素为0。因此反对称函数K(v,w)可写作

K(w,w)-K(w,v)-K(v,w)+K(v,v)=0，∀v∈Ω∀w∈Ω

(15)

定义3[3]函数K(v,w)在Ω×Ω上为斜对称函数，如果满足下面的不等式

K(w,w)-K(w,v)-K(v,w)+K(v,v)≥0，∀w∈Ω，∀v∈Ω

(16)

显然，反对称函数一定是斜对称函数。

如果K(v,w)关于第二元w是凸的，则有

〈∇wK(w,w)-∇wK(v,v),w-v〉≥0，

∀w∈Ω∀v∈Ω

(17)

由式(7)的形式能得到

∇wΦ(v,w)|w=v=∇wS(v,w)|w=v+∇wK(v,w)|w=v

(18)

如果目标函数Φ(v,w)关于第二元w可微时，则由式(2)可以得到

〈∇wΦ(v*,v*),w-v*〉≥0，∀w∈Ω

(19)

将式(11)和式(18)代入到式(19)可以得到

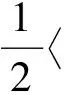
w-v*〉≥0 ∀w∈Ω

(20)

另一方面，若K(v,w)关于第二元w都是凸的，则根据式(14)和式(17)可以得到

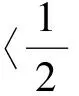
再根据式(18)可以得到

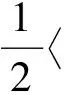
(21)

此外，∇wΦ(v,v)满足Lipschitz条件如下

|∇wΦ(v+h,v+h)-∇wΦ(v,v)|≤L|h|

(22)

其中L为Lipschitz常数。

投影算子在将变分不等式问题转化为等式时起着重要的作用，下面介绍投影算子的定义及与其相关的重要引理。

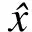
引理1[15]设H是实希尔伯特空间，C⊂H是闭凸集合。对给定的z∈H，u∈C满足不等式

〈u-z,v-u〉≥0, ∀v∈C,

当且仅当u-ΠC(z)=0。

2 二阶微分方程系统

本节将要讨论运用二阶微分方程系统求解极值映射不动点问题(1)的方法。

当Φ(v,w)关于第二元w∈Ω可微时，如果v*∈Ω*是问题(1)的不动点，则v*一定满足下面的变分不等式

〈∇wΦ(v*,v*),w-v*〉≥0，∀w∈Ω

(23)

根据引理1变分不等式(23)可等价为下面的方程

v*=ΠΩ(v*-α∇wΦ(v*,v*))

(24)

其中α>0，πΩ(·)为集合Ω上的投影算子。

注1：显然式(23)和方程(24)是极值映射不动点问题(1)的必要条件；若Φ(v,w)关于第二元w∈Ω可微且凸时，则式(23)和方程(24)与原始问题(1)等价。

为求解变分不等式(23)和方程(24)，建立二阶微分方程系统。与Antipin[3]相似，建立下面的具有控制过程的二阶微分方程系统。

(25)

其中μ>0,β>0和α>0是参数。

根据引理1，可将微分方程系统(25)转化为变分不等式

(26)

(27)

下面给出二阶微分方程系统的轨迹聚点是变分不等式问题(23)的解。

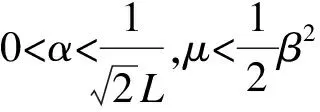
证明：在式(26)中w=v*得到

(28)

利用内积与范数的关系计算得

(29)

运用式(22)，式(25)及投影算子的非扩张性和内积与范数的关系，对式(29)中的第3项进行处理

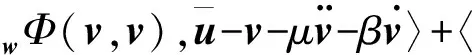
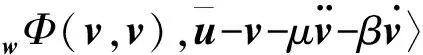
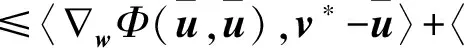
∇wΦ(v,v)‖‖ΠΩ(v-α∇wΦ(v,v))-

将上式代入式(29)可以表示为

(30)

利用内积与范数的关系计算得到

(31)

将式(30)与式(31)相加得到

(32)

由于已知条件∇Sw(v,w)|w=v存在，P(v)是凸函数，K(v,w)关于第二元w可微且凸，根据式(7)和式(21)可以得到

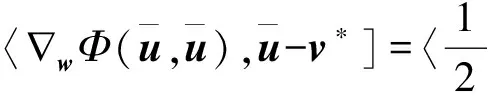
(33)

根据式(33)的估计，式(34)可以写成

(34)

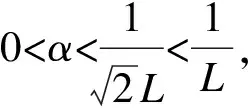
利用内积和范数的关系得到

‖x+y‖2=‖x‖2+2〈x,y〉+‖y‖2, ∀x,y∈Rn

(35)

根据式(35)可以得到

将上式代入到式(34)中可得

(36)

再由下面的关系

对式(36)的前两项进行计算

将上面的结果代入到式(36)中得到

(37)

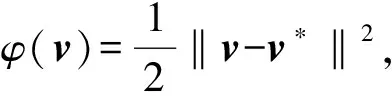
(38)

对式(38)从t0到t积分可以得到

(39)

其中C1=μφ′(v0)+βφ(v0)+

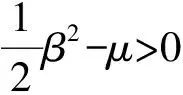
(40)

求解该常微分方程得

(41)

对式(41)从t0到t积分可以得到

继续计算可得

(42)

由式(42)可得‖v-v*‖2有界。

再根据式(39)可得

(43)

在上式中令t→∞，则有

(44)

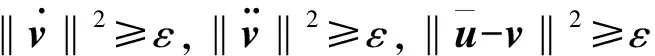
v′=ΠΩ(v′-α∇wΦ(v′,v′))

则有v′满足式(24)，即v′是变分不等式(23)的解。根据注1，如果函数Φ(v,w)关于第二元w是凸函数时，则v′是极值映射不动点问题(1)的解。

3 数值结果

用微分方程式(25)求解两个实际问题，应用Matlab R2019a软件进行计算。在求解过程中,所采用的具体算法是微分方程求解函数ode45,这个函数采用的是四阶五级的Runge-Kutta方法。选取参数α=0.01,μ=0.1,β=0.5。计算机的配置为：CPU Intel(R)Core(TM)i7-7700HQ @2.80 GHz；内存为16.0 GB。

例1 考虑下面双人博弈问题[1]

x*∈argmin{f(z)+L(z,p*):z∈Q},

p*∈argmin{φ(y)-L(x*,y):y∈P}

(45)

其中函数f(z),φ(y)为凸函数，L(z,p)为不动点函数。其典型的具体情况如下

x*∈argmin{0.5(z-1)2+zp*:z∈R1},p*∈argmin{0.5(y-3)2+x*y:y∈R1}

(46)

Antipn[1]给出了式(46)的解(x*,p*)T=(-1，2)T。

为了应用微分方程式(25)求解，设

Φ(v,ω)=f(ω1)+L(ω1,v2)-L(v1,ω2)+

φ(ω2),

其中ω=(ω1,ω2)T=(z,y)T,v=(v1,v2)T=(x,p)T。

图1描绘了双人博弈问题式(46)的微分方程式(25)的解的轨迹随时间的变化关系，而且该图的曲线是微分方程式(25)的解的轨迹从9个不同随机选取的初始点生成的。经过微分方程式(25)求解得到该系统的轨迹v=(x,p)T收敛于平衡点v=(-1.007 2,2.004 4)T,即式(46)的近似解。

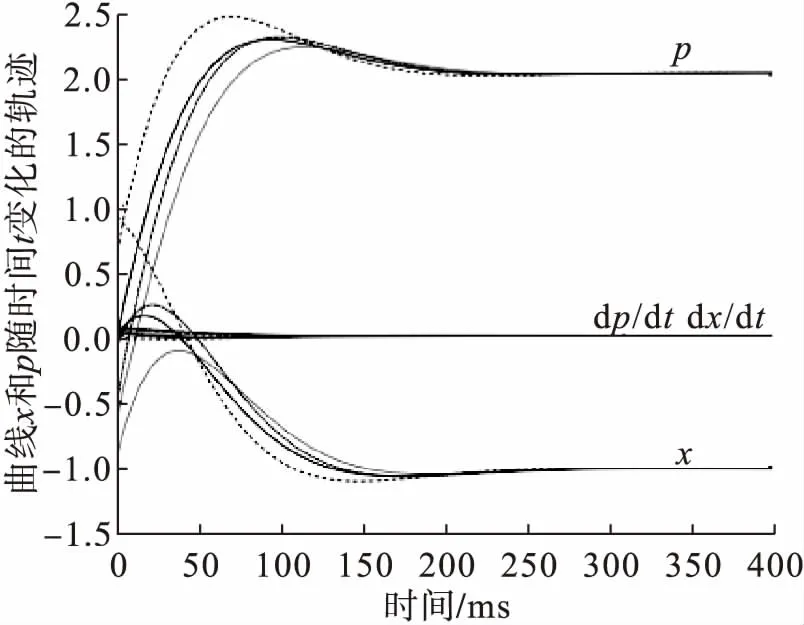
图1 双人博弈问题式(46)的微分方程系统式(25)的解的轨迹

例2考虑下面极值映射不动点问题[2]

v*∈arg min{0.5〈Nw,w〉+〈Mv*+m,w〉|w∈Ω}

(47)

其中N和M是非负矩阵，并假设矩阵N是对称的。

图2描绘了极值映射不动点问题式(47)的微分方程式(25)解的轨迹随时间的变化关系，而且该图的曲线是微分方程式(25)的解的轨迹从8个不同随机选取的初始点生成的。经过计算微分方程式(25)求解该系统的轨迹v=(v1,v2,v3)T收敛于(-0.372 7,-0.093 6,-0.044 6)T,即问题式(47)的近似解。

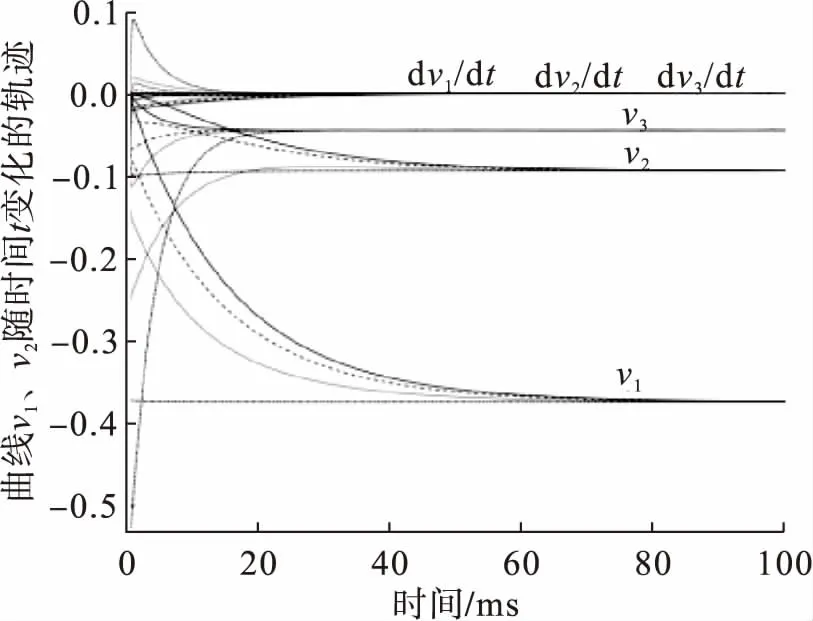
图2 极值映射不动点问题式(47)的微分方程式(25)的解的轨迹

4 结论

Antipin[3]研究了极值映射的不动点问题(1)的一阶微分方程方法，提出了对称函数、伪对称函数、反对称函数及斜对称函数的定义，并指出了对称函数与伪对称函数、反对称函数与斜对称函数的关系，同时得到了这些函数偏导数的一系列性质。运用这些性质建立了一阶微分方程系统，本文在此基础之上建立了具有控制过程的二阶微分方程系统，并证明了具有控制过程的二阶微分方程系统的轨迹的聚点是极值映射不动点问题(1)的解。除得出理论结果，本文也具体计算了Antipin[1]和Antipin[2]提出的两个具体问题，得到了运行结果，证明了具有控制过程的二阶微分方程系统求解极值映射不动点问题(1)的有效性。