基于试验设计方法的梯形波纹板片极限承载能力研究
魏筱婷,马一鸣,陈冠羲,冯栩迟,付宝琛,李晓峰
(1.甘肃蓝科石化高新装备股份有限公司,甘肃 兰州 730070;2.上海蓝滨石化设备有限责任公司,上海 201518)
板式热交换器属于一种典型的高效、紧凑式热交换器,被广泛应用于石油炼化、热能与动力工程等流程工业领域。节能增效、绿色环保的高质量发展趋势,促使板式热交换器的应用场合加速拓展,市场占比份额快速提高。板式热交换器应用场合的高参数化以及产品轻量化发展趋势[1-3],迫切需要提出行业公认的板片波纹机械设计方法与评价指标,以保障产品安全。国内制造企业一般依赖各自的工程实践经验,确定不同板型板片的许用压力与厚度的对应关系,未形成公认的可验证的设计方法。国外知名制造企业对基于载荷的波纹板设计方法未见公开报道。ASME标准虽然以附录、标准案例[4-5]形式给出了板片波纹承载能力评价的基本原则,但具体实施细则难以操作。BФ Павленко[6]关于板片波形选择的试验也未形成指导文件。试验设计(Design of Experiments,DOE)方法是一种科学安排试验和分析试验数据的方法,是通过有目的地安排尽量少的试验数量找到响应与因子之间的关系,以较少的试验次数获得科学的试验结论。本文基于DOE方法,研究了梯形波纹板片的临界压缩力与波高和截面夹角的关系,以期为后续制定板式热交换器工程设计方法与指标提供借鉴。
1 梯形波纹板片极限承载能力研究内容
1.1 板片失效模式确定
板式热交换器板片的常见波纹形式为人字形,波纹横向截面为等腰梯形,在承受法向递增压力载荷时,相互接触形成网状支撑。在初始加载阶段,板片结构处于稳态,压缩变形量随载荷增加线性变化。当载荷提高到一定程度时,会导致板片突然垮塌[7],突变起始点的板片初始失效。因此,文中以板片发生明显变形时的法向载荷作为板片的临界载荷。
1.2 板片承载能力影响因素
波纹板片的承载能力取决于板片的材料性能、成型工艺及结构参数。文中主要研究结构参数对板片承载能力的影响,暂不考虑材料性能、成型工艺的影响。波纹板片的结构参数主要包括波高、展开系数、厚度、截面形状、波顶半径和转角半径等[8-10]。 对于波纹板式热交换器,波高、展开系数既是机械参数,也是重要的工艺参数。而厚度是重要的机械参数,对于工艺的影响可忽略不计。因此首先研究波高和展开系数对承载能力的影响。
板片材料选用S30408,考虑应用经济性,板片厚度固定为0.6 mm。波纹横向截面为等腰梯形,底宽3.5 mm。波顶为直线平壁,转角半径固定为0.5 mm。板片结构变化参数为,波高3~8 mm,展开系数1.09~1.45,根据波高和展开系数折算的截面夹角为35°~60°。波高及展开系数范围基本涵盖常规板片板型。梯形波纹板片设计模型截面形状及几何尺寸见图1。
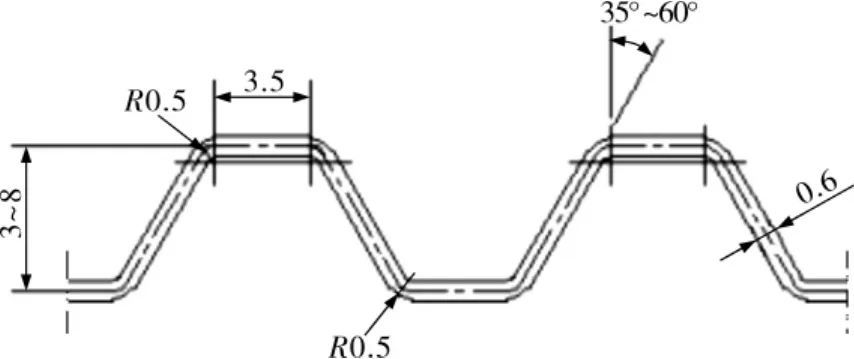
图1 梯形波纹板片设计模型截面形状及几何尺寸
2 梯形波纹板片极限承载能力DOE分析及结果
2.1 响应、因子、试验类型及因子水平确定
响应Y是试验的输出、试验中的因变量。因子X是决定Y的关键因子,为试验中的自变量,可以是离散型或数值型数据。范围是每个因子的极值,决定因子的试验区域。水平是每个因子1个或多个不同的取值。
梯形波纹板片极限承载能力试验的输入为法向载荷,响应Y为板片失稳临界压缩力。可控因子设置为截面夹角X1和波高X2,截面夹角X1为35°~60°,波高X2为3~8 mm。板片滑移量对于板片承载能力是有利因子,使试验结果较为保守,因此将板片滑移量设置为噪声因子,试验中不予考虑。梯形波纹板片极限承载能力试验参数图见图2。

图2 梯形波纹板片极限承载能力试验参数图
梯形波纹板片极限承载能力试验研究中确定的显著性因素数量不多,故DOE方法中采用响应曲面设计[11]。两水平因子设计的模型不能有效描述有显著曲面特性的响应曲面,而三水平可以拟合二次项或者更高次项方程模型的响应,因此试验选用三水平因子设计。
2.2 DOE及结果分析
采用两因子三水平中心复合设计生成试验计划表,试验模式共9组,见表1。
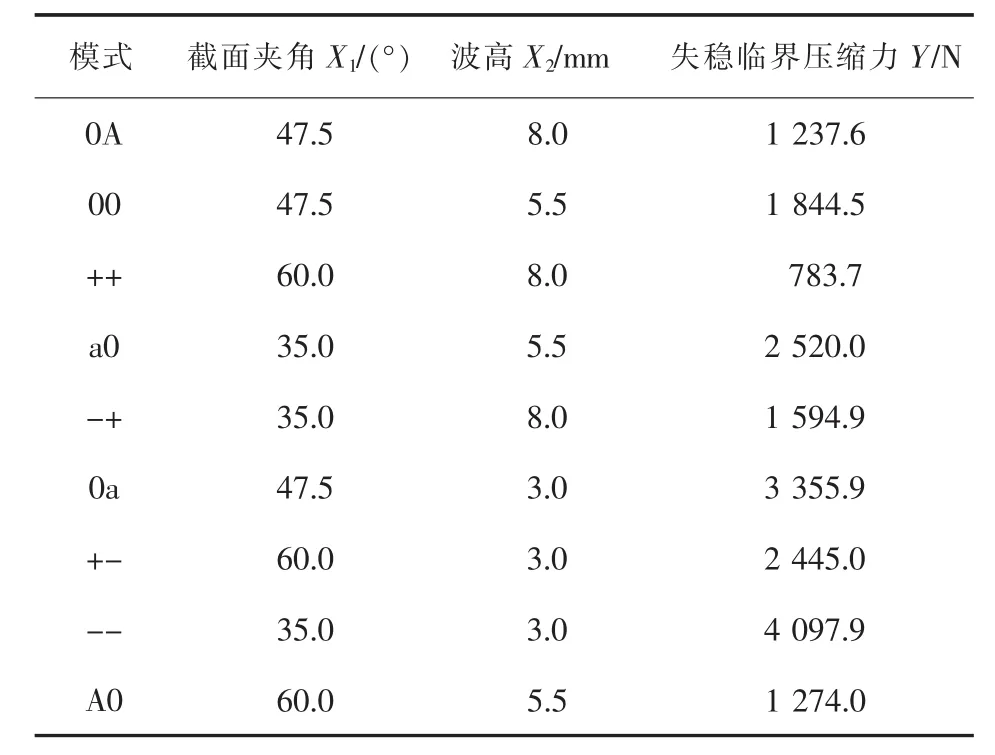
表1 梯形波纹板片极限承载能力试验计划及结果
根据表1,借助有限元应力分析手段[12],计算出不同因子水平组合对应的板片失稳临界压缩力,进行模型初步拟合。
梯形波纹板片有限元模型见图3。模型横向截面为等腰梯形,厚度0.6 mm,顶宽3.5 mm,转角半径0.5 mm,截面夹角及波高尺寸组合方式按照表1。为简化分析难度,采用平面应变模型模拟波纹承载[13]。考虑模型承载时的大应变效应,分析采用基于大变形的弹塑性计算方法[14-15]。同时,为准确获取板片临界响应,输入载荷按随时间递增设置(图4),并根据计算结果是否收敛判断计算重点。
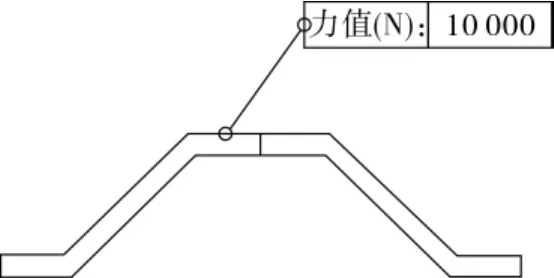
图3 梯形波纹板片有限元模型
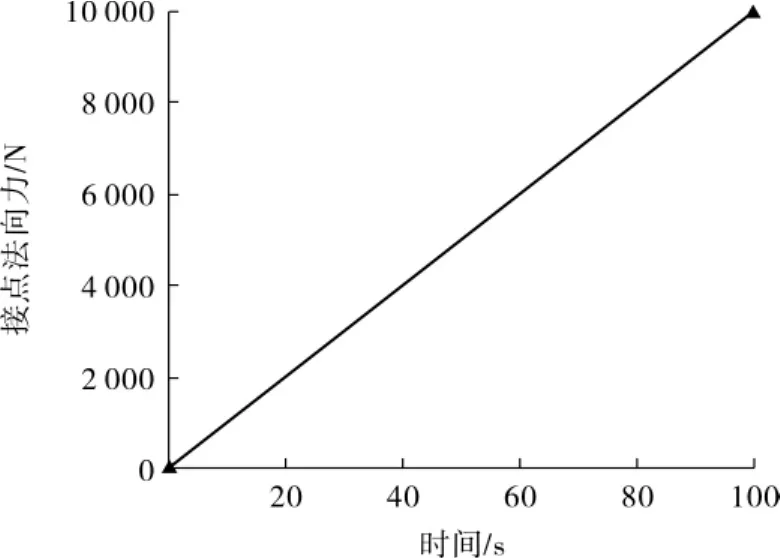
图4 梯形波纹板片有限元计算输入载荷
有限元分析得到的梯形波纹板片反作用力与时间响应曲线见图5。由图5可以看出,塑性垮塌前,板片结构处于弹性稳定状态,系统反作用力与输入载荷相互呼应,呈线性变化。发生临界垮塌时,板片整体结构丧失稳定性,刚度呈现非线性,反作用力发生跳跃。以发生2次跳跃的反作用力作为结构临界载荷,结果见表1。
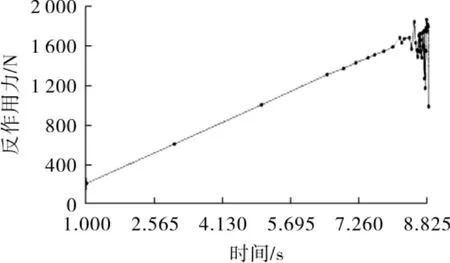
图5 梯形波纹板片反作用力与时间响应曲线
采用最小二乘法多项式拟合法对数据进行响应面拟合,拟合阶数为二阶,得到的初步拟合效应P值(概率)见表2。从表2可以看出,波高X2、截面夹角 X1、波高X2×波高X2、截面夹角 X1×波高X2对应的P值均小于0.05,说明这些参数及交互作用对板片临界压缩力的影响是显著的,且波高对临界压缩力的影响最大,截面夹角的影响次之。截面夹角X1×截面夹角X1对应的P值远大于0.05,说明截面夹角间的交互作用对板片临界压缩力的影响不显著。
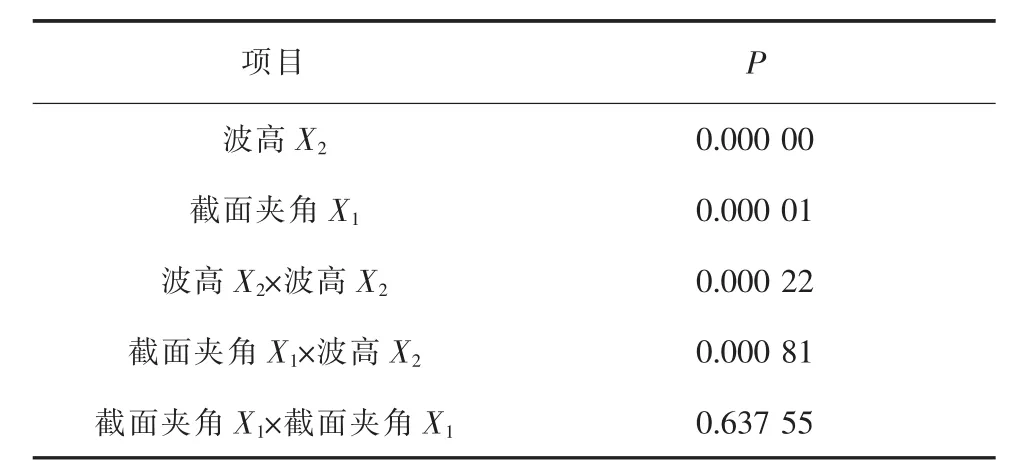
表2 梯形波纹板片初步拟合效应P值
剔除非显著二次项截面夹角X1×截面夹角X1,重新拟合板片模型,得到拟合效应P值及估计值t(t为回归系数与回归系数标准误差的比值)的排列,见表3。
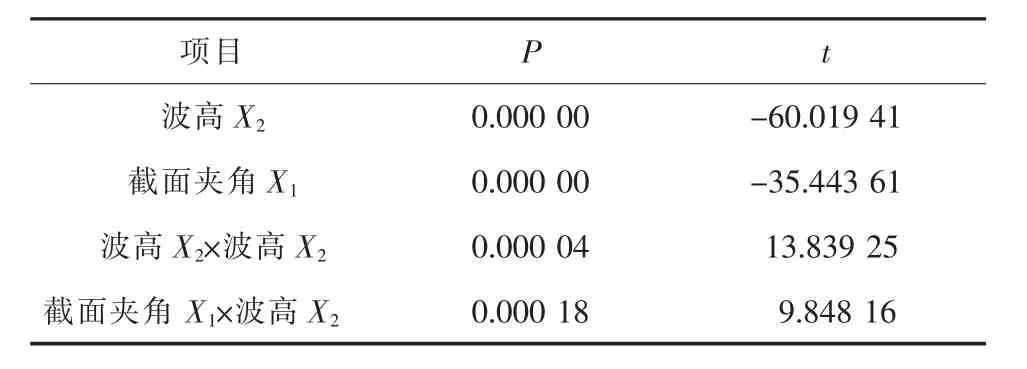
表3 剔除非显著二次项后梯形波纹板片拟合效应P值及估计值t排列
从表3可以看出,P值均比初步拟合模型的低,即各参数及交互作用对板片临界压缩力的影响都显著提高,说明该模型比初步拟合模型有所改进。
表3中t的数值反映出波高X2、截面夹角X1与临界压缩力呈现负相关,波高、截面夹角增大,临界压缩力减小,板片承压能力降低。此结论与文献[16]中所获结论一致,也验证了文中研究的正确性。
一般认为,R2(回归方程中的残差占总方差的分数)越接近1,表明拟合程度越好。此次拟合的R2=0.999 03,说明模型拟合程度较好。调整R2=0.998 253,与R2非常接近,表明建立的模型较正确。
根据数据拟合结果,在波高3~8 mm,截面夹角35°~60°内,梯形波纹板片失稳临界压缩力Y与板片截面夹角X1和波高X2的响应面模型拟合方程为:
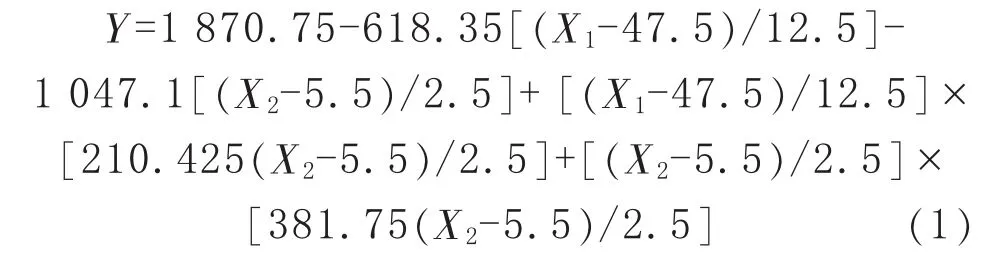
2.3 拟合方程验证
选择拟合方程适用范围内的1组参数截面夹角 X1=45°、波高 X2=3.7 mm,代入式(1)得到梯形波纹板片临界压缩力预测值为2 976 N。以相同参数进行应力仿真分析计算,得到的梯形波纹板片临界压缩力分析值为2 949 N(图6)。拟合方程预测值与仿真分析值相近,误差约1%,说明拟合方程正确性较高。
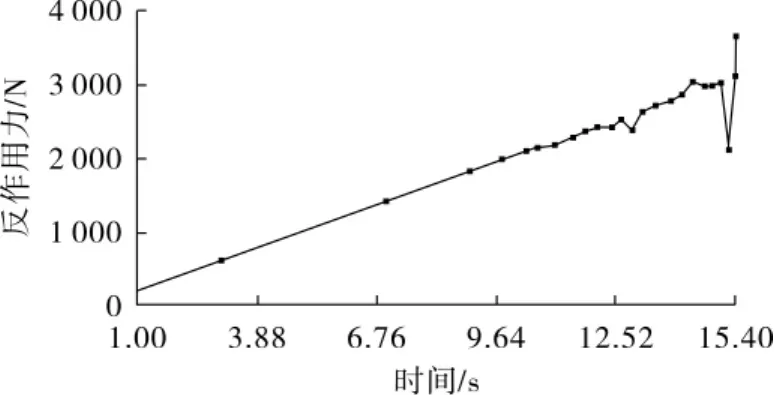
图6 梯形波纹板片临界压缩力仿真分析结果
3 结语
基于DOE方法对梯形波纹板片进行的极限承载能力研究表明,板片波高、截面夹角与板片临界压缩力呈现负相关,波高、截面夹角增大,临界压缩力减小,板片承压能力降低。通过DOE得到了梯形波纹板片失稳临界压缩力与波高和截面夹角的拟合方程,拟合方程计算结果与仿真软件计算验证结果非常相近,证明了拟合方程的正确性。基于拟合方程,可以预测不同波高和截面夹角板片的临界载荷,为改善板片结构参数、确定板片失效条件提供理论支撑。
文中仅研究了板片波高和截面夹角对板片临界载荷的影响,后续还需增加板片厚度、转角半径等因素的研究,补充试验,完善拟合方程,明确更多因素与板片极限承载能力的关系,扩大拟合方程适用范围。

