高中数学临界生立体几何学习现状及教学策略

陈庆芳

高中数学临界生立体几何学习现状及教学策略

陈庆芳

（广东省肇庆市高要区第一中学,广东肇庆526100）

作为教师，只有深入地掌握学生的学习实际情况，才能更好地进行因生施教和因材施教，方能令教学效果达到最大化的要求。本文笔者采用问卷调查、测试（前测与后测）调查、个案研究、基于SPSS的数据统计分析、教学设计和教学实验等研究方法，对高中数学临界生立体几何学习现状进行调查分析及教学策略研究，并为提高高中数学临界生立体几何的学习成绩提供相关的教学经验以及教学建议。

数学临界生；立体几何；对比研究；个案研究；教学实验

在学习过程当中，临界生具有非常大的发展潜力，做好他们的教学工作是中学教育成功的关键。如果教师能够加强临界生的教学工作，不仅可以促进高中教育教学工作的全面发展，探索出一条新的高中生教育模式，实现新形势下的高中教学培养目标，并且能使更多的学生在高考中脱颖而出，考出理想的成绩。

经参考有关文献，以及在有关专家的指导下，并结合自己的工作实际情况，笔者在本课题研究的临界生对象是针对高考总分能进入普通本科线而数学单科成绩不能进入普通本科线的高中学生。

一、研究对象

本文研究对象是广东省肇庆市高要区第一中学2020年入学的学生。广东省肇庆市高要区第一中学于1998年被评为广东省一级学校，并且是广东省的示范性高中，见微知著，选择此校的高中数学临界生进行立体几何学习的调查分析研究，统计的结果具有一定的典型性和代表性。

（一）数学临界生界定方法

1.2023年高考总分上本科线预测。搜集、整理广东省肇庆市高要区第一中学2017～2021年的高考本科升学率。利用统计回归分析法，预测2023年广东省肇庆市高要区第一中学的高考本科升学率，见图1所示。

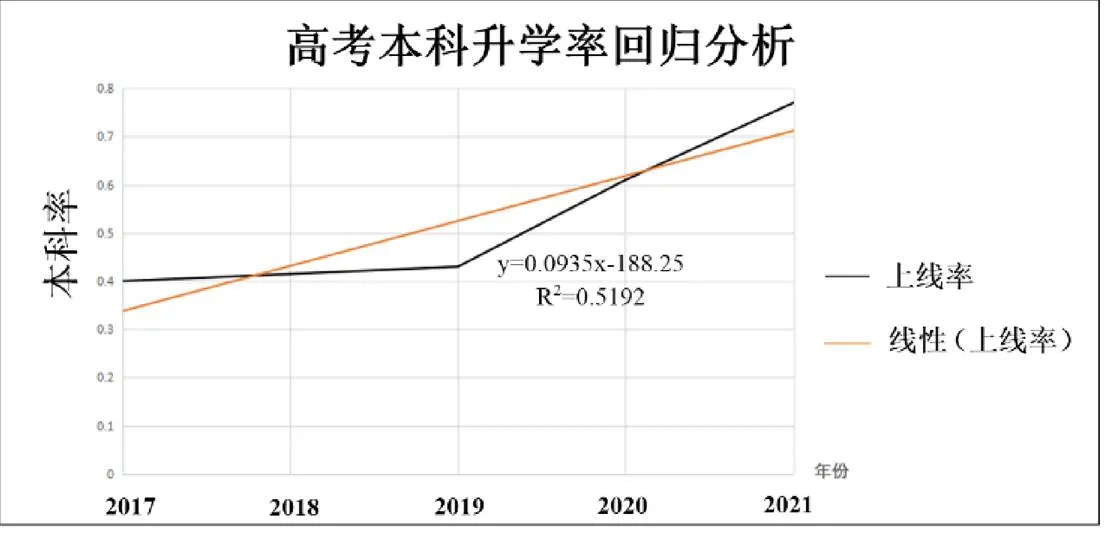
图1　高考本科升学率回归分析

从图1可以看出，2023年广东省肇庆市高要区第一中学的本科预测升学率公式为y=0.0935x-188.25，考虑到每年高考都会存在各种不确定因素，所以在升学率公式里面引入不确定系数i。不确定系数i是根据每年高考前的高考模拟考试成绩进行统计分析得出，最终的本科预测升学率公式调整为y=i（0.0935x-188.25）。经计算知2023年广东省肇庆市高要区第一中学的本科升学人数约为696人（注：这只是初步统计分析的数据，作为课题研究使用。等到2023年高考前高考模拟考试成绩出来后进行相关统计分析后得出较准确的不确定系数i，将i代入本科预测升学率公式计算方可得出较准确的本科升学率预测值）。

2.2023年高考数学单科上本科线预测

搜集、整理广东省肇庆市高要区第一中学2017～2021年的高考数学单科上本科线的吻合率。利用统计回归分析法，预测2023年广东省肇庆市高要区第一中学的高考数学单科上本科线的吻合率，见图2所示。

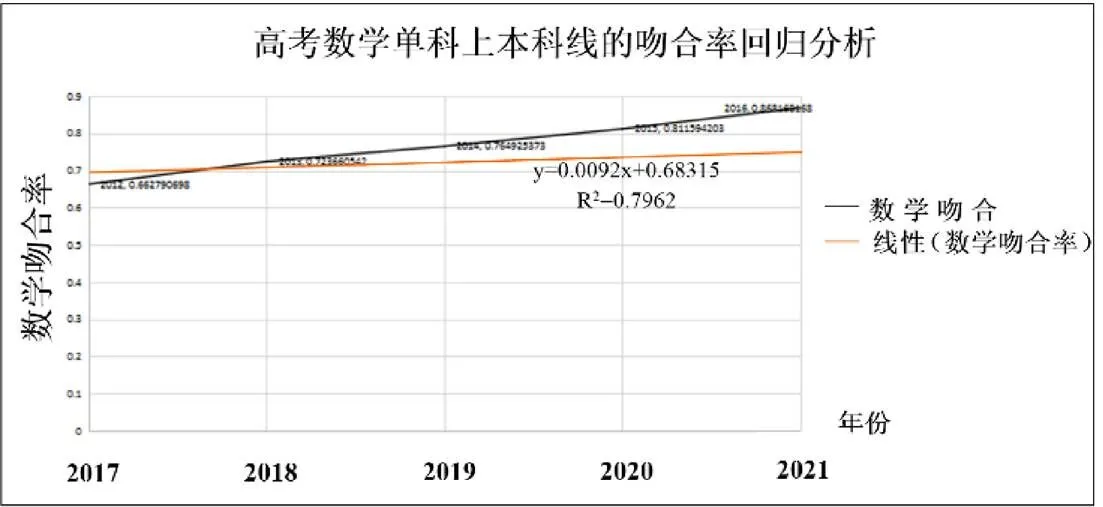
图2　高考数学单科上本科线的吻合率回归分析

从图2可以看出，2023年高考数学单科上本科线预测升学率公式为y＝0.0092x+0.68315，考虑到每年高考都会存在各种不确定因素，所以在升学率公式里面引入不确定系数j。不确定系数j是根据每年高考前的高考模拟考试成绩进行统计分析得出，最终的预测升学率公式调整为y=j（0.0092x+0.68315）。经计算知2023年广东省肇庆市高要区第一中学的数学单科本科升学人数约为601人（注：这只是初步统计分析的数据，作为课题研究使用。等到2023年高考前高考模拟考试成绩出来后进行相关统计分析后得出较准确的不确定系数j，将j代入预测升学率公式计算方可得出较准确的本科升学率预测值）。

3.数学临界生界定方法

经以上初步计算知2023年广东省肇庆市高要区第一中学的总分达到本科分数线的人数约为696人，其中数学单科成绩达到本科分数线的人数约为601人。根据反吻合率计算，得知总分能进入本科线，但数学单科成绩不能进入本科线的学生人数约为95人，根据上下浮动原理，取数学临界生的总人数为190人，即这190位学生的数学单科成绩是处于数学单科本科临界线上下浮动的特定范围区间内。

二、调查过程与分析

在本调查研究中，问卷和测试卷都是围绕六个维度展开的，如图3所示。

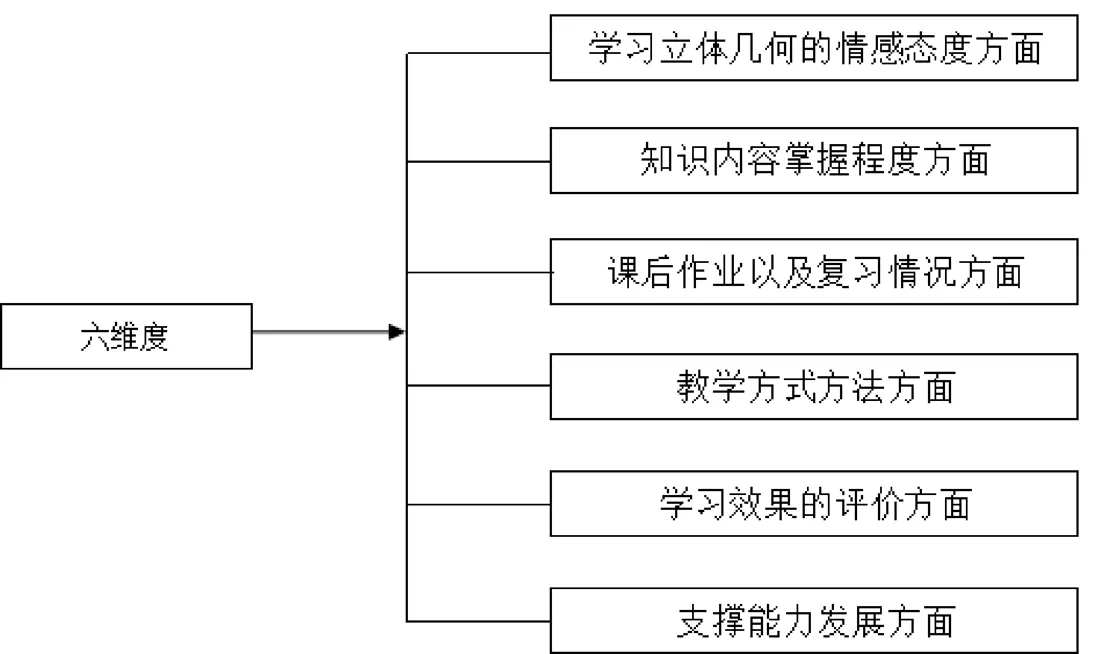
图3　六维度图

高中数学临界生调查问卷的设计是参照文献以及相关方面的研究，在有关专家的指导下自行设计的；测试卷（前测与后测）是根据考试大纲的要求，围绕六个维度需要测试考核的相关内容进行出题的。

在数学临界生调查问卷和测试卷（前测与后测）的设计过程中，基本都是围绕这六个维度，并遵循的原则是：

（1）能通过询问得出结果的问题就用调查问卷问；

（2）不能通过询问得出结果的问题就用测试卷（前测与后测）测。

特别利用一个高中晚自习的时间，分别进行了一次问卷调查和测试（前测）调查。

（一）问卷调查分析

调查问卷共设13道选择题，主要是针对数学临界生进行不记分和不计名的调查。特利用高中晚自习时间发放，并且15分钟之后收回。累计共发放190份问卷，收回190份问卷，有效190份问卷，其中问卷用SPSS分析的信度为0.705，如表1所示，效度为0.726，如表2所示，所有的统计数据都在合理区间内（相关标准参考DeVellis，Kaiser等学者提出的关于信效度的研究结果，这些研究结果表明：在探索性研究中，对于教师自编的问卷调查进行数据统计，信效度在0.7～0.8范围内，可以被认为是较高水平。）表明数据可靠。

表1问卷数据可靠性统计量

表2问卷数据KMO和Bartlett的检验

（二）测试调查分析

测试（前测）调查共3道大题，3道大题分别是选择题、填空题和解答题。选择题每题5分，共60分，填空题每题5分，共20分，解答题中的第一题为10分，其余题目为12分，共70分，整张测试卷总分为150分，用时120分钟。通过由笔者主持的项目——广东省肇庆市高要区中小学教育科研课题《基于数学核心素养的高中数学临界生立体几何教学策略应用研究》课题组主要参与成员进行集体手工改卷，分数比较真实可靠。测试卷主要考查学生的知识点包括以下12点内容，如图4所示。

测试人数190人，有效人数190人，通过SPSS软件进行统计分析，试卷信度为0.719，如表3所示，效度为0.734，如表4所示，试卷的难度指数为0.42，所有的统计数据都在合理区间内（相关标准参考DeVellis、Kaiser等学者提出的关于信效度的研究结果，这些研究结果表明：在探索性研究中，对于教师自编的测试卷进行数据统计，信效度在0.7～0.8范围内，可以被认为是较高水平。），表明测试数据可靠。

表3前测试卷数据可靠性统计量

表4前测试卷数据KMO和Bartlett的检验

利用SPSS软件对测试卷里面的得分情况进行统计分析，统计分析的内容包括数学临界生做每道题的得分情况分析，数学临界生做每道题的得分以及试卷总分的差异性分析。

（三）个案研究分析

选取研究对象范围内立体几何成绩最好、中等以及最差的学生进行个案研究，研究方法是学生访谈。学生访谈是在学生调查问卷已有的问题基础上，对选取的学生对象进行个别谈话，目的是想更进一步了解在学习过程中数学临界生立体几何学习情况以及差异性。

（四）数学临界生教学实验分析

1.实验对象

经回归计算得知2023年广东省肇庆市高要区第一中学的总分达到本科分数线的人数约为696人，其中数学单科成绩达到本科分数线的人数约为601人，根据反吻合率计算，得知总分能进入本科线，但数学单科成绩不能进入本科线的学生人数约为95人。根据上下浮动原理，取数学临界生的总人数为190人，即这190位学生的数学单科成绩是处于数学单科本科临界线上下浮动的特定范围区间内。

2.实验设想

实验班根据教师最新设计的教学方式进行上课，主要针对前面的调查分析的结果，对数学临界生掌握立体几何知识点较薄弱的环节以及数学临界生差异性较大的知识内容进行讲解与训练，目的是提高数学临界生立体几何的解题能力以及缩小数学临界生学习立体几何之间的差异。

3.教学实验过程设计

教学实验是依托由笔者主持的项目——广东省肇庆市高要区中小学教育科研课题《基于数学核心素养的高中数学临界生立体几何教学策略应用研究》展开的，课题组主要参与成员共7名高中数学教师。

教学实验过程中所涉及到的标准、教学案例以及授课方法是在参考《中学数学课程标准》、有关文献、相关教材以及在有关专家的指导下，由笔者自行编排与设计的。参与实验的学生共190人，有效人数190人，这些学生的教学以及辅导工作由以上提到的课题组主要参与成员共7名高中数学教师负责，这7名高中数学教师是依据笔者设计的授课方法进行授课以及开展相关辅导工作。教学实验过程总设计流程图，如图5所示。

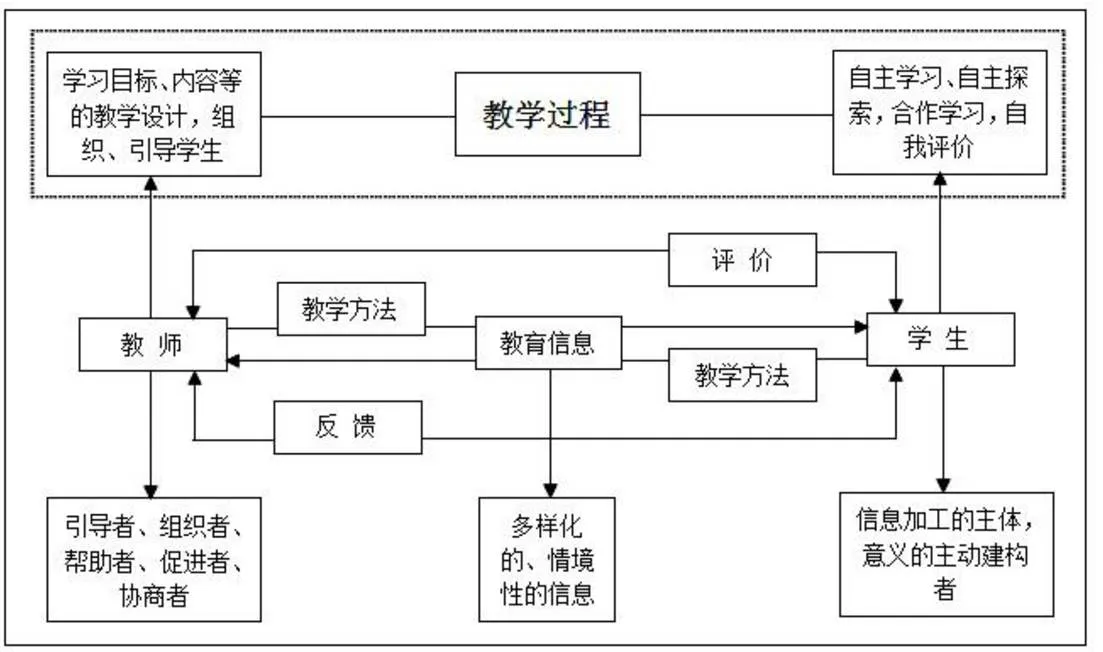
图5　教学实验过程总设计流程图

教学方法：通过实例式讲解、案例互动式讨论、研究式探索以及反馈式评价等授课方式充分发挥学生的主体地位，营造生动活泼的课堂教学氛围。

学习方法：实践探索、观察发现、类比猜想、合作沟通、规范训练。

教学工具：通过借助多媒体计算机（幻灯片、几何画板、实物投影等）进行辅助教学，从而增强课堂教学的生动性与直观性。

（1）典型教学情况

根据前面的调查分析结果，将数学临界生大致分成两类（A类和B类），得出以下主要结论，如图6所示。

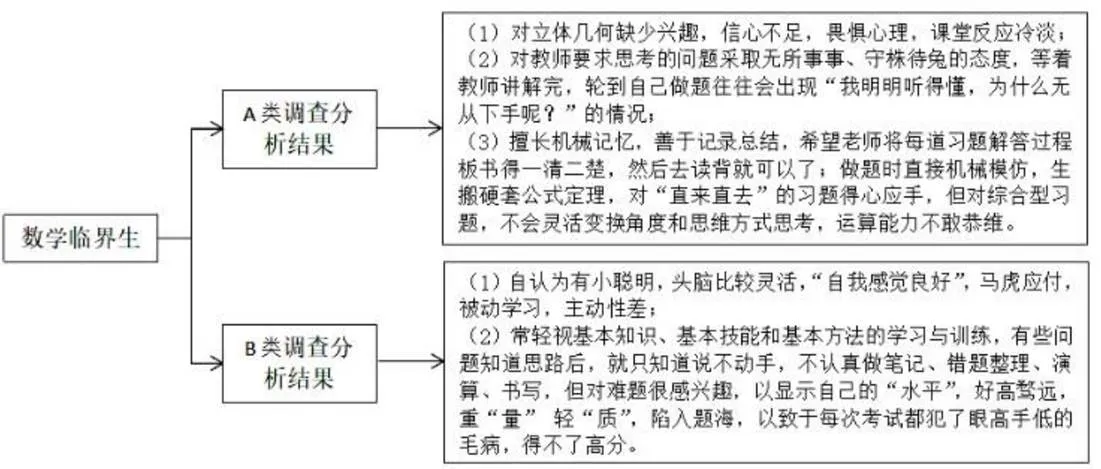
图6　数学临界生调查分析结果

（2）应对策略

针对前面的数学临界生调查分析结果，得出相应的应对策略，如图7所示。

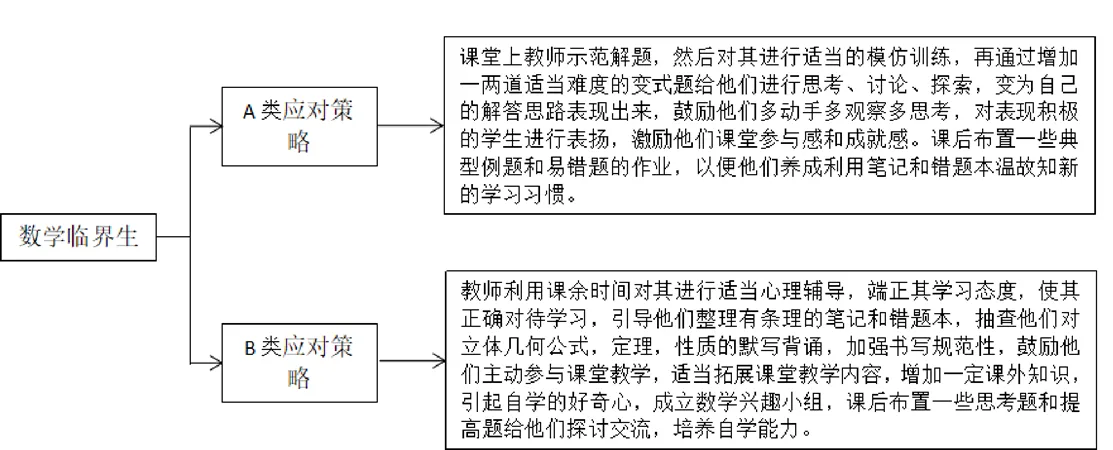
图7　数学临界生应对策略

4.实验结果统计与分析

笔者经过对实验班的学生采用新的教学方式进行授课后进行新一轮的测试（后测），测试（后测）调查共3道大题，3道大题分别是选择题、填空题和解答题。选择题每题5分，共60分，填空题每题5分，共20分，解答题中的第一题为10分，其余题目为12分，共70分，整张测试卷总分为150分，用时120分钟。通过由笔者主持的项目——广东省肇庆市高要区中小学教育科研课题《基于数学核心素养的高中数学临界生立体几何教学策略应用研究》课题组主要参与成员进行集体手工改卷，分数比较真实可靠。

测试人数190人，有效人数190人，通过SPSS软件进行统计分析，试卷信度为0.748，如表5所示，效度为0.753，如表6所示，试卷的难度指数为0.48（比前测卷的难度指数要大），所有的统计数据都在合理区间内（相关标准参考DeVellis，Kaiser等学者提出的关于信效度的研究结果，这些研究结果表明：在探索性研究中，对于教师自编的测试卷进行数据统计，信效度在0.7～0.8范围内，可以被认为是较高水平。），表明测试数据可靠。

表5后测试卷数据可靠性统计量

表6后测试卷数据KMO和Bartlett的检验

利用SPSS软件对测试卷里面的得分情况进行统计分析，统计分析的内容包括数学临界生做每道题的得分情况分析，数学临界生做每道题的得分以及试卷总分的差异性分析。

用SPSS软件统计的前测试卷的数学临界生不同题目的得分率，如图8所示。

图8　前测试卷的数学临界生不同题目的得分率

用SPSS软件统计后测试卷的数学临界生不同题目的得分率，如图9所示。

图9　后测试卷的数学临界生不同题目的得分率

由图8和图9可以看出，经过对实验班的学生进行新一轮的测试结果表明，对实验班的学生采用新的教学方式进行授课后是有一定的教学效果的，原来得分较低的题目，现在得分提高了，另外数学临界生的差异也缩小了。

三、研究结论

本文笔者采用问卷调查和测试（前测与后测）调查、个案分析研究、基于SPSS的数据统计分析、教学设计和教学实验等研究方法，对高中数学临界生立体几何学习现状进行调查分析及教学策略研究。研究结果表明：

1.A类数学临界生、B类数学临界生在对于学习立体几何的情感态度上都显得比较低，相比A类数学临界生，B类数学临界生在学习兴趣等方面表现较突出。

2.就掌握立体几何知识的内容而言，数学临界生普遍认为，比较难以证明空间线线、线面、面面垂直和难以进行整体立体几何知识框架的建立，相比较来说这方面B类数学临界生掌握得比较好。

3.大多数数学临界生认为，在立体几何作业量及作业难度方面都比较适中，但有部分A类数学临界生认为教师布置的课后作业难度较大、课后的作业量较多；相比较来说B类数学临界生在一种问题使用多种解法、举一反三的能力方面做得比较好，而A类数学临界生比B类数学临界生更擅长做错题整理以及课后归纳总结做笔记。

4.大多数数学临界生在教师的指导下，基本上都掌握了学习立体几何的方式方法，同时他们也喜欢教师使用三维立体教学模型作为教具，并配合现代信息技术进行相关的辅助教学，相比较来说B类数学临界生做得较好。

5.大多数数学临界生在学习立体几何效果的测试与评价方面都做得比较不好，相比较来说B类数学临界生做得比较好。

6.就学习立体几何支撑能力方面而言，大多数数学临界生能力较低。与A类数学临界生相比，B类数学临界生的这方面能力相对较高，主要体现在计算能力、动手能力方面表现较好，但A类数学临界生比较细心。

四、教学建议

基于本文的研究分析结果和有关实验班的对比教学实验，笔者从以下几个方面对高中数学教师提出关于数学临界生立体几何的教学建议，如图10所示。

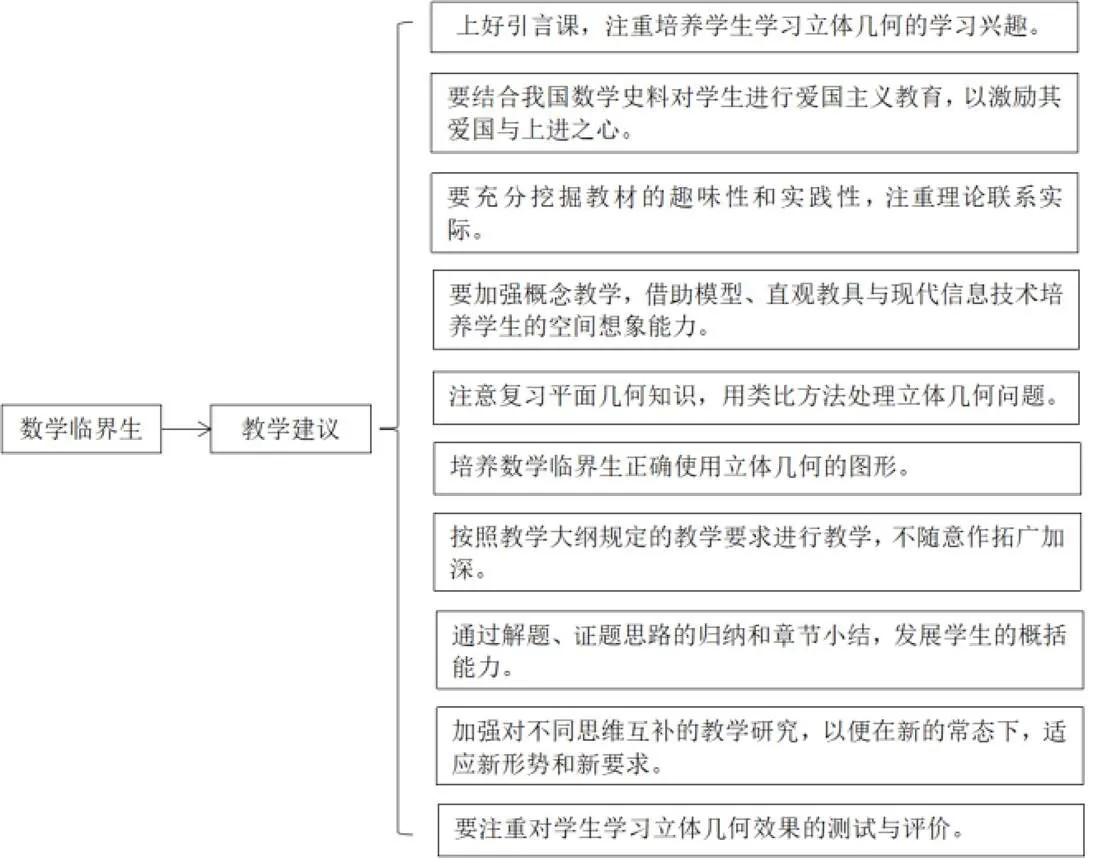
图10　数学临界生立体几何的教学建议

五、教学案例

（一）利用教学直观法培养学生的空间想象能力在立体几何教学中可以通过四种直观教学培养学生的空间想象能力，尤其是对女生，如图11所示。

在平面上画出空间图形的直观图，是培养空间想象能力与掌握几何概念的必经途径，是学习立体几何的一大难关。因此教师必须重视借助模型、实物、直观教具与现代信息技术逐步形成学生的空间观念，发展学生的想象能力，从有模型画图到减少以至不需模型直接按画法规则画出空间图形，逐步提高学生的能力。

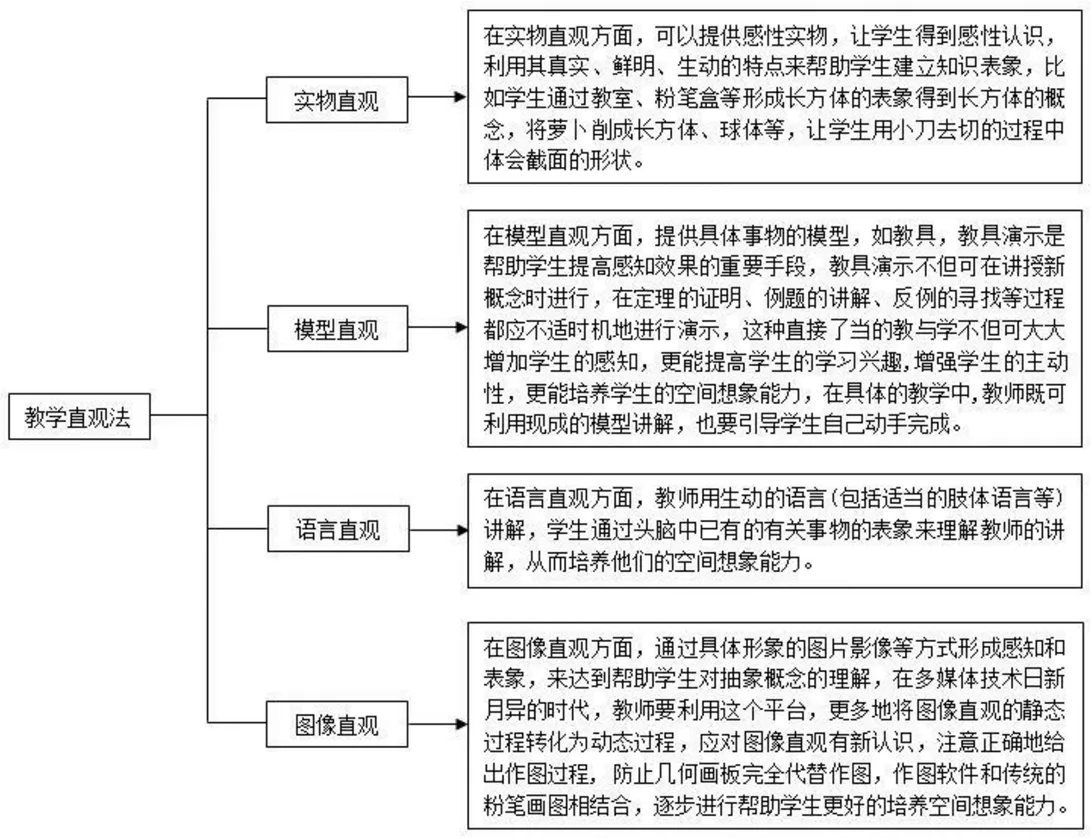
图11　教学直观法

（二）在立体几何中，不同的画法可以应用于同一个立体图形。至于采取什么样的画法，必须要根据具体情况，使所画的图形能突出具体问题中要重点观察的那部分内容，并且具有一定的真实立体感。

例：两个平面α、β相交于AB，交角为120˚，点P到平面α、β的距离分别为PC＝3cm，PD＝2cm，求点P到AB的距离。

分析：此题可以画成图12中（1）、（2）、（3）三种图形，显然画成图（3），就更直观一些。事实上，从图中即可看出，作出P到AB的垂线PE，及PC⊥α，PD⊥β，据三垂线定理得CE⊥AB，所以P、C、E、D共面且共圆。于是问题归结为求平面上四边形PCED的外接圆的直径，显然，不难求出PE的值。

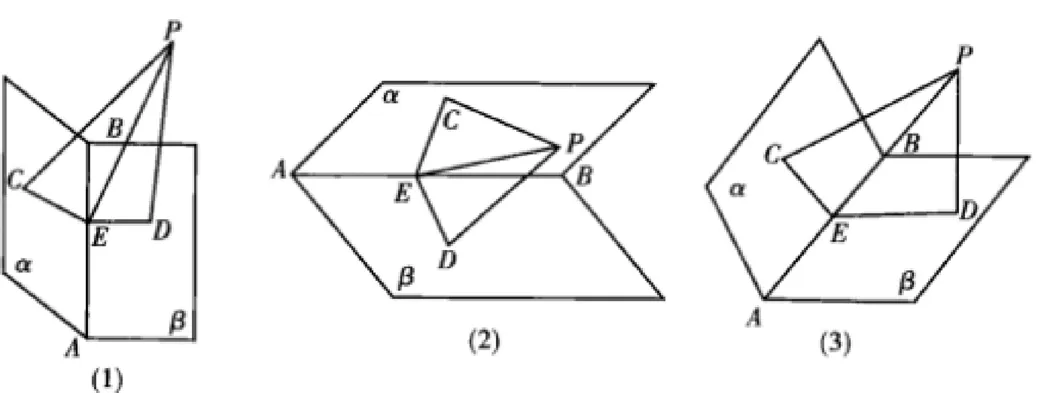
图12　图例

立体几何教学过程不仅在图形的观察上有它的特殊性，而且在作图上更有其特点。

教师要正确地画出立体图形（直观图），不仅要掌握并能熟练地运用平行投影和中心投影的一些基本知识，而且还需要特别注意在作图过程中不断分析有关的线、面和角之间的关系，不然将难以准确、合理地画出需要的图形。

（三）在知识系统化的过程中提高学生的概况能力

例如，立体几何中求各种各样的角，两异面直线所成的角、直线与平面所成的角、平面与平面所成的角（二面角），可概括为各种不同形式的角，最后总是转化为相交直线的角来度量。

再如立体几何中位置关系的判断和证明：可概括为如图13所示。

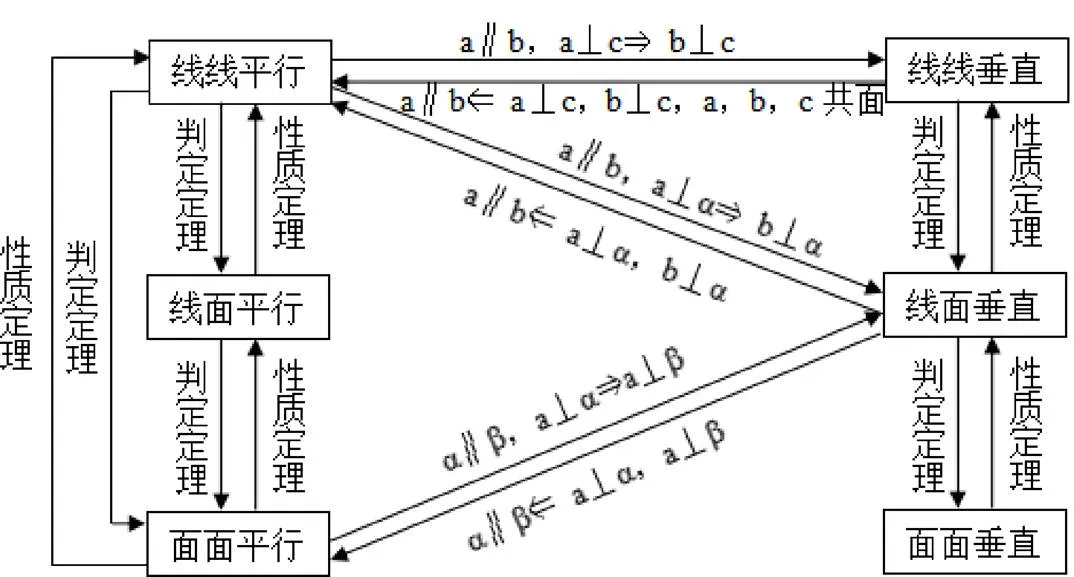
图13　立体几何中位置关系的判断和证明

（四）理论联系实际

要充分挖掘教材的趣味性和实践性，注重理论联系实际。例如，可以组织学生汇集一些实例验证平面的三个基本性质，让学生看到生产或生活中找不到一个实例能否定这三个基本性质，从而加深对平面基本性质的理解。又如，在黑板上寥寥数笔，勾画出菜刀、斧头等图形，引进二面角概念，学生跃跃欲试，兴趣油然而生。

（五）教学内容不随意作拓广加深

按照教学大纲规定的教学要求进行教学，不随意拓广加深。例如，在讨论用斜二测画法画水平放置的平面图形时，所画图形主要是正三角形、正方形、正六边形，不宜搞得复杂。在位置要求上主要是水平放置状态，不要扩大到垂直位置状态及任意位置状态，更不要补充画法理论。

（六）结合我国数学史料对学生进行爱国主义教育

我国古代对几何体体积的计算就有过比较系统的研究，如《九章算术》中的长方体、方锥和圆锥、方亭和圆亭（即正棱台和圆台）、刍甍与刍童（即楔体和长方形底面的拟柱体）、立圆（即球）的计算公式；刘徽的“损广补狭”“棋验法”“截面法”；祖暅的“缘幂势既同，则积不容异”及“体积之比等于对应截面积之比”的论述等等成果卓著。教师可结合教学内容，使学生对这些历史有所了解，以激励其爱国与上进之心。

六、不足与启示

（一）不足的地方

1.在本课题的调查研究中，由于受到了各方面的条件限制，目前只是采用了问卷调查、访谈调查以及测试（前测与后测）调查等方式方法，而未采用全面调查法对高中数学临界生学习立体几何的现状做调查研究，研究面可能不够广。

2.这次研究，笔者是在紧张繁忙的高中教学工作以及要承担沉重家务劳动的时间之余，抽空进行相关的研究工作，时间精力都非常有限。另外，研究过程当中要用到的数据统计分析、现代教学设计原理与方法等方面的知识，而数据统计分析等方面的知识并不是笔者专业所擅长，所以有关方面的知识储备并不充分，可能导致研究的方法不够全面。

3.在研究的过程中，笔者选取调查的学生时，只对高中数学临界生学习立体几何的学习思维等方面的差异性进行了调查研究分析，但是并没有考虑学生性别方面、父母亲的文化程度方面、家庭背景方面、住宿方面等影响因素，以致分析出来的差异性结果可能并不完整。

4.由于受到各方面条件的限制，只选择了笔者所教年级的学生进行调查研究分析，可能会导致研究人数不多的情况出现，以致影响研究结果。在以后的研究中，有待扩展到对整个学校所有年级的学生进行研究，提高研究结果的准确性。

（二）启示

本学校正在推行“适性扬才，多元发展”的教学模式，并取得了一定成效。如何在具体的教学模式下归纳分析造成高中数学临界生立体几何学习困难的原因，提出立体几何课堂教学活动中面向全体数学临界生和因材施教相结合的教学策略，提高学生的数学成绩，最终养成良好的数学思维习惯和能力，是重点需要解决的问题。

[1] 王小燕.高中生立体几何必修二的学习现状调查研究[D].兰州:西北师范大学,2015.

[2] 池国升.《课标》背景下立体几何学习障碍的调查研究[D].福州:福建师范大学,2014.

[3] 杨娟.高中生立体几何解题策略差异性的调查研究[D].重庆:西南大学,2016.

[4] 涂荣豹.数学教学设计原理的构建——教学生学会思考[M].北京:科学出版社,2018.

[5] 徐福荫,袁锐锷.现代教育技术基础[M].北京:人民教育出版社,2005.

O123.2,C45

A

1002-7661(2022)05-0162-06

本文系广东省肇庆市高要区中小学教育科研课题“基于数学核心素养的高中数学临界生立体几何教学策略应用研究”（编号：2020GYJYKYKT015）研究成果。