走出复数问题的几个误区
赵久果
(山东省邹平市第一中学)
数系扩充后,有关数的一些难以解决的问题得到了解决,如负数可以开方,任何一元二次方程在复数域上有解.但我们也要看到新概念的完善过程并非一帆风顺,实数内的一些运算规则有些仍可执行,有些却已被打破.因此,我们在求解复数问题时必须“提高警惕”,才能“走出误区”.
1 混淆复数的有关概念
复数是实数的扩充,虚数和实数都是复数的组成部分,纯虚数隶属虚数,它的虚部不可为零.
例1若复数z=lg(m2-2m-2)+(m2+3m+2)i是纯虚数,则m的值为________.
错解由lg(m2-2m-2)=0,得m2-2m-2=1,则m=3或-1.

综上,m=3.

复数是数的大家庭,其成员有实数与虚数,而虚数又含有纯虚数,纯虚数的实部一定是零,实部为零的数不一定是纯虚数,如实数0.
2 忽视两个复数相等的条件
由复数相等,可以得到方程组,进而将复数问题实数化,但解题时必须注意自变量或参数的属性.
例2若x∈C,则满足(x2-4x+3)+(x2-6x+5)i=0的x的值为_________.


综上,x=1.
剖析在两个复数a+bi,c+di相等的充要条件中,前提条件是a,b,c,d∈R,即当a,b,c,d∈R 时,a+bi与c+di相等的充要条件是a=c且b=d.这里的x2-4x+3和x2-6x+5不一定是复数的实部和虚部,因为这里的x∈C,故本题应采用类似于一元二次方程的因式分解法来处理.
正解由(x2-4x+3)+(x2-6x+5)i=0,可得(x-1)[(x-3)+(x-5)i]=0,所以x=1 或(x-3)+(x-5)i=0,由(x-3)+(x-5)i=0,可得(1+i)x=3+5i,所以x==4+i.
综上,x=1或4+i.

在明确题目中的未知数是实数时,可采用复数相等的充要条件建立方程组来解未知数;当未知数的范围不明确时,将未知数设为复数的代数形式,再根据复数相等的充要条件解之.
3 忽视“xt=(xm)n⇒m·n=t”成立的条件
实数范围内的运算法则有时可以移植到复数的计算中,有时却不行,必须注意相关条件.

剖析在实数集中,对任意x∈R(m,n∈R),有xmn=(xm)n;而在复数集中,仅对m,n∈N*有xmn=(xm)n.此错解盲目地将实数集中的指数运算法则直接推广到了复数集.


复数的运算法则与实数的运算法则有区别,不可盲目套用.
4 忽视“x2=|x|2”的适用范围
当x∈R时,x2=|x|2成立,当x∈C时,它就不一定成立了.所以在实数范围内成立的结论不可盲目地搬到复数范围内运算.
例4方程x2-5|x|+6=0在复数范围内的解的个数为_________.
错解由x2-5|x|+6=0,得(|x|-2)(|x|-3)=0,故|x|=2或|x|=3,从而x=±2或x=±3,故解的个数为4.
剖析本题中的未知数并不是实数,但上述解答把它当成实数来解.把实数的绝对值与复数的模混为一谈,事实上,在复数范围内x2=|x|2是不成立的.因为该式左侧依然是复数,而右侧一定是实数.
正解设x=a+bi(a,b∈R),那么原方程即为(a+bi)2-6=0,得
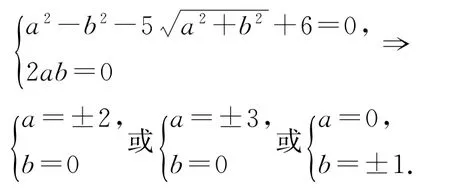
综上,所求方程的解的个数为6.

当x为虚数时,x2=|x|2不成立,因为这时x2仍可能是虚数,而|x|2是实数.
5 忽视两个复数能比较大小的条件
当复数的虚部不为0时无法比较大小,只有当它是实数时才可以比较大小.所以复数可以比较大小的前提条件是它们必须是实数.
例5求使x+2+(x+y)i>y-5+(x+2y-3)i成立的实数x,y的取值.
错解1复数无法比较大小,所以这是一道无法解答的错题.
错解2由得y<3,且x+7>y.
剖析本题的隐含条件是不等式的左、右两侧都是实数.错解1没有发现这个隐含条件,而错解2更荒唐地认为“实部与虚部都分别大的复数较大”.
正解由题意知x+2+(x+y)i与y-5+(x+2y-3)i 均为实数,故可得解得

复数固然无法比较大小,但实数可以比较大小,复数的模可以比较大小.对于这类问题必须认真审题,发现隐含条件.
6 忽略判别式法判断根的前提
在处理一元二次方程根的问题时,判别式法只适用于实数范围.当方程中出现虚数时,这个方法失效.
例6求实数k,使方程x2+(k+2i)x+2+ki=0至少有一个实根.

剖析如果一个一元二次方程的系数是实数,那么可以采用判别式法来判定它的根的情形,可本题是一个复系数的一元二次方程,这时判别式法就“失灵”了,我们必须严格遵循复数的“游戏规则”.


对于复数集上的一元二次方程ax2+bx+c=0是否存在实数根,Δ=b2-4ac≥0,既不是充分条件,也不是必要条件,判别式法仅在实数集内有效,对于复系数一元二次方程问题,一般可将未知数设为复数的代数形式,然后利用复数相等的充要条件转化为方程组来解.
从以上错解可以看出,求解复数问题的最大误区就是把它当成实数问题来处理.因此,我们解复数问题时一定要注意它与实数的区别与联系,解有关复数问题时一定要严格遵循复数的运算法则,有时还可以结合复数的几何意义来分析问题,从而达到解决问题的目的.
(完)

