材料拉压弹性模量差异对路面倒装结构力学性能的影响

牛敏强，邓明超，蔡 良，苑苗苗

(1.广东省南粤交通仁博高速管理中心新博管理处，广东 惠州 516899；2.广东省南粤交通大丰华高速公路管理中心，广东 梅州 514329；3.华南理工大学广州学院，广东 广州 501800)

1 前 言

目前，我国现行的公路沥青路面设计规范对路面结构进行力学分析时采用弹性层状体系理论，该理论将路面材料假定为各向同性体，即在不同的应力状态下材料的拉伸和压缩性能是一致的，在材料参数方面表现为拉压模量以及泊松比均相同。然而，道路材料拉伸和压缩力学性能明显不同，若仅采用单一的压缩模量表征材料的力学性能将导致路面材料的力学性能被高估，使得路面结构计算结果与实际工作状态严重不符，极大影响路面在服役中力学响应及长期性能[1-4]。实际上，工程上较多的材料存在拉伸和压缩性能各异的特征，这常常导致采用该材料修筑的工程结构拉压力学行为明显不同[5-8]。

而对于筑路材料，几乎绝大部分的路用材料也具有类似的性质。吕松涛等[9-11]对沥青混合料和水泥稳定碎石的拉压模量进行测定，研究发现这两种材料的拉伸和压缩模量差别较大，其中压缩模量约为拉伸模量的1.5～2倍。因此，将道路材料看作拉压模量不同的材料，在路面结构计算过程中，根据路面结构中各个积分点的拉压应力状态相应赋予材料不同的拉压模量及泊松比，建立符合材料实际服役性能的材料参数模型，对设计出合理的路面结构具有重要意义。

基于此，以拉压不同模量理论为基础，通过ABAQUS有限元软件的UMAT用户子程序功能，将拉压模量不同的材料本构进行二次开发，通过对比以常规压缩模量为材料参数模型的数值模拟结果进行对比，研究拉压模量不同对路面结构力学响应分析结果的影响。

2 理论基础

2.1 不同拉压模量理论基本概念

目前，对于材料拉压模量不同的研究主要分为两大类：一种是以复合材料为代表的正交各向异性固体和连续体；另外一种是对各向同性材料，但拉伸和压缩式的力学行为存在明显差异。对于第二种材料本构模型，Ambartsumyan[12]进行了系统的研究，并发展形成了拉压不同模量的弹性理论。该理论可以采用分段的直线函数对不同拉压模量材料的应力-应变关系曲线进行近似表达(如图1所示，其中E+为受拉弹性模量，E-为受压弹性模量)，该简化模型具有足够的精度，完全满足工程应用的要求[13]。本研究也采用该模型进行沥青路面结构层拉压模量差异对路面结构力学性能进行研究。

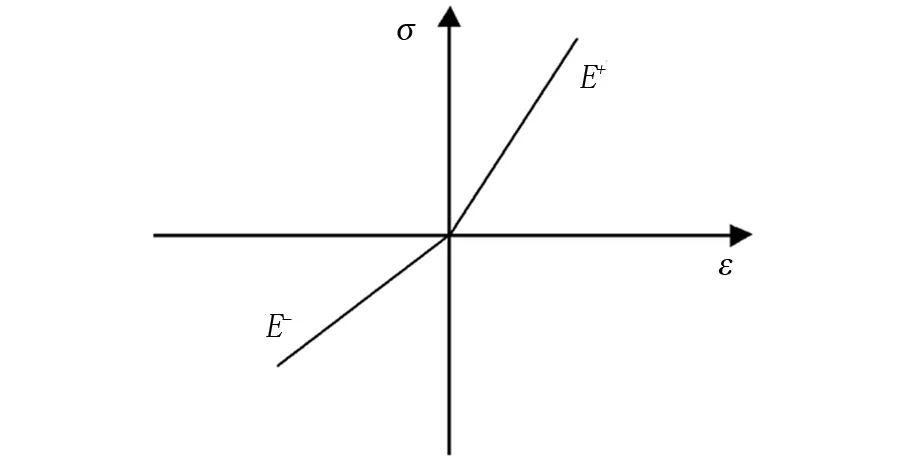
图1 拉压不同模量材料的双直线应力-应变模型

2.2 基本假设

(1)研究的对象是连续的、均匀的弹性体；

(2)在任意应力状态下只发生弹性小变形；

(3)各点的计算弹性参数根据主应力符号的不同，分别赋予不同的弹性模量与泊松比；

(4)假设μ+/E+=μ-/E-。

3 本构关系与有限元模型的建立

3.1 不同拉压模量本构关系

分段的直线函数中，材料的本构关系根据主应力的拉压不同，弹性模量及泊松比分别取值：当主应力为正时(受拉)，弹性模量及泊松比分别为E+及μ+；当主应力为负时(受压)，弹性模量及泊松比分别为E-及μ-。因此，根据经典弹性理论建立以下基于主应力方向的二维本构方程

(1)

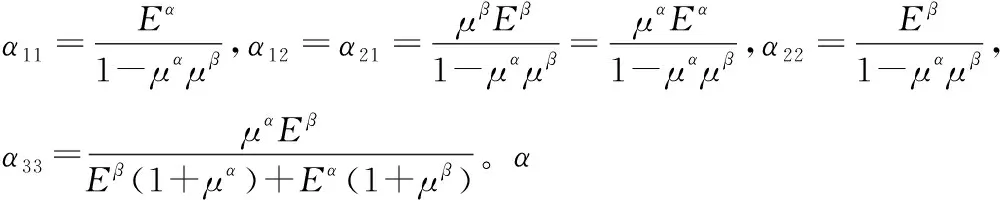
ABAQUS在数值计算过程中，主程序和用户子程序UMAT相互之间存在数据传递的协同工作过程。其主要工作原理如下：在每个增量步开始时，主程序给节点施加一个外力增量，然后主程序通过UMAT子程序接口进入UMAT，单元当前高斯积分点相关的变量的初始值随之传递给UAMT子程序相应的变量，ABAQUS会根据上一增量步提供的切线刚度矩阵计算出节点位移变量，然后形成新的刚度矩阵并进行迭代计算，直至收敛为止，获得收敛后的应变增量和应力增量，最后通过子程序接口将这些变量的更新值返回给主程序，进入下一个增量步进行求解计算。ABAQUS调用UAMT子程序的详细过程如图2所示。

图2 ABAQUS主程序调用UMAT流程

以上面层沥青混合料为例，其二维拉压不同模量本构UMAT的子程序采用Fortran语言编写主要步骤如下。

(1)定义初始变量。

1DDSDDT(NTENS)，DRPLDE(NTENS)，

STRAN(NTENS)，DSTRAN(NTENS)，

2TIME(2)，PREDEF(1)，DPRED(1)，PROPS(NPROPS)，COORDS(3)，DROT(3，3)，

3DFGRD0(3，3)，DFGRD1(3，3)

REAL(KIND=8)：：ESHE(NTENS)，DESHE(NTENS)，RESHE(NTENS)，VSHE(NTENS)

REAL(KIND=8)：：DSSHE(NTENS)，DSTRES(NTENS)，D(NDI，NDI)

REAL(KIND=8)：：Q11，Q12，Q13，Q21，Q22，Q23，Q31，Q32，Q33，EMOD，ENU，EBULK3，EG2，EG，EG3，ELAM，K1，K2

REAL(KIND=8)：：DDSDDE(3，3)，DSTRESS(3)，EMODcompression，ENUcompression，EMODtension，ENUtension

EMODcompression=PROPS(1)

ENUcompression=PROPS(2)

EMODtension=PROPS(3)

ENUtension=PROPS(4)

(2)定义初始弹性刚度，以层状弹性体系计算值为初始值

IF(ABS(KINC-1.0).LE.1.0E-3)THEN

EMOD=1500000000.0

ENU=0.3

EBULK3=EMOD/(1-2*ENU)

EG2=EMOD/(1+ENU)

EG=EG2/2

EG3=3*EG

ELAM=(EBULK3-EG2)/3

DO K1=1，NDI

DO K2=1，NDI

DDSDDE(K2，K1)=ELAM

END DO

DDSDDE(K1，K1)=EG2+ELAM

END DO

DO K1=NDI+1，NTENS

DDSDDE(K1，K1)=EG

END DO

ELSE

(3)以X方向主应力受压，Y方向主应力受拉为例，求解材料本构关系的雅可比矩阵(DDSDDE矩阵)。

IF(STRESS(1).LT.0..AND.STRESS(2).LT.0.)THEN Q11=EMODcompression/(1.0-ENUcompression*ENUcompression) Q12=EMODcompression*ENUcompression/(1.0-ENUcompression*ENUcompression)

Q13=0.0

Q21=Q12

Q22=EMODcompression/(1.0-ENUcompression*ENUcompression)

Q23=0.0

Q31=0.0

Q32=0.0

Q33=EMODcompression/(1.0+ENUcompression)/2.0

C更新DDSDDE的值

DDSDDE(1，1)=Q11

DDSDDE(1，2)=Q12

DDSDDE(1，3)=Q13

DDSDDE(2，1)=Q21

DDSDDE(2，2)=Q22

DDSDDE(2，3)=Q23

DDSDDE(3，1)=Q31

DDSDDE(3，2)=Q32

DDSDDE(3，3)=Q33

(4)计算应力增量DSTRESS，并更新应力STRESS。

DSTRESS(1)=DDSDDE(1，1)*DSTRAN(1)+DDSDDE(1，2)*DSTRAN(2)+DDSDDE(1，3)*DSTRAN(3)

DSTRESS(2)=DDSDDE(2，1)*DSTRAN(1)+DDSDDE(2，2)*DSTRAN(2)+DDSDDE(2，3)*DSTRAN(3)

DSTRESS(3)=DDSDDE(3，1)*DSTRAN(1)+DDSDDE(3，2)*DSTRAN(2)+DDSDDE(3，3)*DSTRAN(3)

DO t=1，3

STRESS(t)=STRESS(t)+DSTRESS(t)

END DO

RETURN

END

3.2 有限元计算模型

路面模型在水平方向和深度方向取其有限尺寸，模型的尺寸为5 m(横向)×5 m(纵向)，各结构层厚度及材料参数取值见表1。本研究采用拉压不同模量的模型以及基于压缩模量的模型进行对比分析。沥青层、基层、路基应用四节点双线性平面应力四边形单元(CPS4)进行离散处理，划分有限元网格。网格划分的密度选择自由划分，模型单元数量为4 544，节点数量为4 680。边界条件为：对垂直于路线方向两侧x方向(垂直于路线方向)进行约束；模型底面完全约束。层间接触条件为完全连续。为了便于模型计算，轮胎与路面接触面理想化双轮垂直均布荷载模型，轮胎半径为10.65 cm，双轮中心距31.95 cm，荷载大小为0.7 MPa。

表1 材料参数及模型尺寸

4 典型沥青路面结构力学分析

根据《公路沥青路面设计规范》(JTGD50—2017)，选用如图3所示的计算点位置进行计算分析。其中A点为车轮中心，B点为车轮迹边缘，C点为两个轮胎中心，D点为B点与C点的中点(称为车轮隙r/4处)。

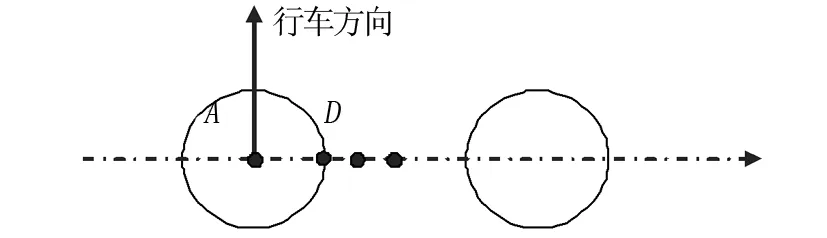
图3 力学响应计算点位置示意图

4.1 横向应力分析

选取A、B、C以及D点，分析两种材料参数模型下沿道路深度方向的横向应力的变化规律。4个分析点的横向应力分析结果如图4所示。由图可知，横向拉应力出现在ATB上基层和水泥稳定碎石底基层。最大横向拉应力出现在水泥稳定碎石底基层层底，且压缩模量模型的两个轮胎中心处以下的水泥稳定碎石底基层层底最大，其中最大层底拉应力为2.757 MPa，拉压不同模量模型最大层底拉应力为2.033 MPa，采用拉压不同模量模型的最大拉应力降低了26.3%。由此可见，基于压缩模量模型的计算结果进行路面设计偏保守。

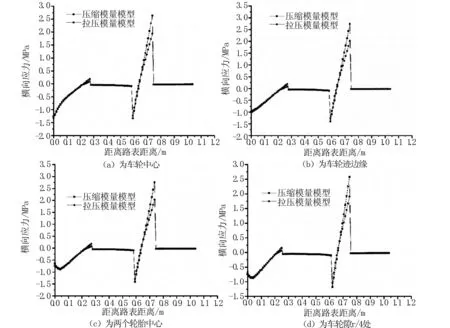
图4 横向应力分析

4.2 横向应变分析

选取A、B、C以及D点，分析两种材料参数模型下沿道路深度方向的横向应变的变化规律。4个分析点的横向应变分析结果如图5所示。由图可知， 横向拉应变出现在ATB上基层、 级配碎石下基层、 水泥稳定碎石底基层以及土基。最大横向拉应变出现在水泥稳定碎石底基层层底，且拉压不同模量模型的两个轮胎中心处以下的水泥稳定碎石底基层层底最大，其中最大层底拉应变为208 με，压缩模量模型最大层底拉应变为184 με，采用拉压不同模量模型的最大拉应变增加了13%。

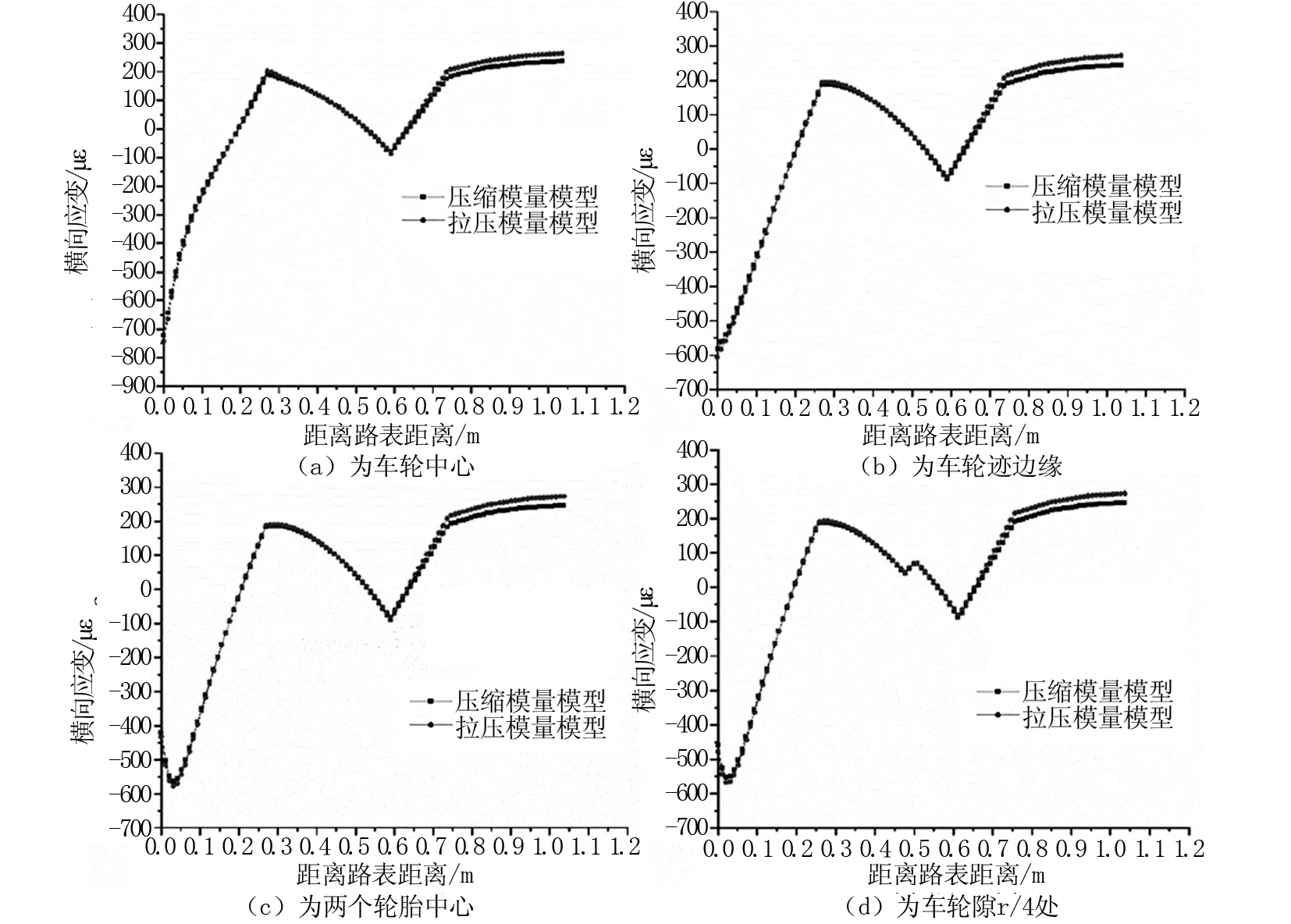
图5 横向应变分析

4.3 剪应力分析

选取A、B、C以及D点，分析两种材料参数模型下沿道路深度方向的剪应力的变化规律。4个分析点的剪应力分析结果如图6所示。由图可知，两个轮胎中心以下的剪应力非常小，最大剪应力出现在车轮迹边缘以下的上面层底，为0.167 8 MPa，此处两种模型的剪应力变化非常小，可忽略不计。

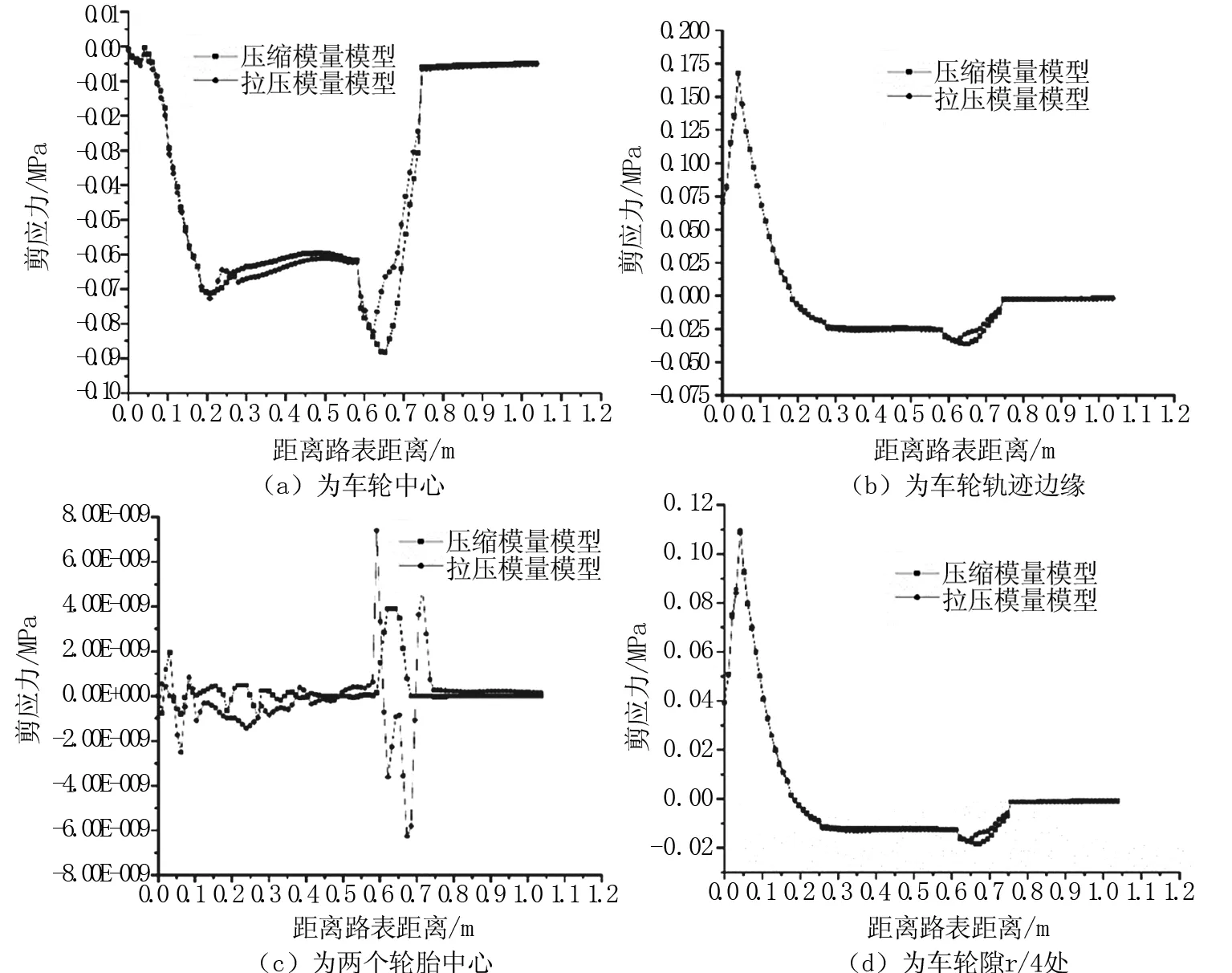
图6 剪应力分析

5 结 论

采用材料拉压不同模量理论，结合ABAQUS有限元UMAT子程序，进行了材料拉压不同模量模型以及基于压缩模量模型的沥青路面结构分析，通过分析路面结构层不同计算点位置的横向应力、横向应变以及剪应力，得到以下结论。

(1)最大横向拉应力出现在水泥稳定碎石底基层层底，且压缩模量模型的两个轮胎中心处以下的水泥稳定碎石底基层层底最大，采用拉压不同模量模型计算得到的最大横向拉应力降低了26.3%。

(2)最大横向拉应变出现在水泥稳定碎石底基层层底，且拉压不同模量模型的两个轮胎中心处以下的水泥稳定碎石底基层层底最大，采用拉压不同模量模型计算得到的最大拉应变增加了13%。

(3)两种模型计算得到的不同计算点位置最大剪应力变化非常小，分析结果可忽略不计。