基于数据结构对共享单车动态调度中的应用分析——以动态调度问题为例

文/王宇（中国地质大学（北京）经济管理学院）

一、选题背景

在最大化满足城市共享单车用户的用车需求以及提高共享单车使用效率等方面，共享单车的动态调度发挥着格外重要的作用，但城市热门用车区域、用车频次与行程结束后的热门停车区域及其停车频次等因素均会直接影响对调度策略的制定，因此共享单车的动态调度问题存在一定的复杂性，为了让共享单车调度策略具有更好的有效性，能将复杂问题简单化的算法将必不可少，所以，本小组对数据结构中的特定算法原理以及其在本市场调度问题中的应用进行展开研究。

二、算法原理

（一）迪杰斯特拉算法

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

（二）哈夫曼树

哈夫曼树（Huffman）又称最优树，是一类带权路径长度最短的树，在实际中有广泛的用途。比如，给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，即哈夫曼树。哈夫曼树中权值较大的结点离根较近。（如：图1）

图1 哈夫曼树

（三）算法拓展

1.遗传算法

遗 传 算 法（Genetic Algorithm，GA）最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换为类似生物进化中的染色体基因的交叉、变异等过程，并被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。

2.启发式算法

启发式算法（heuristic algorithm)是相对于最优化算法提出的。一个问题的最优算法求得该问题每个实例的最优解。启发式算法可以这样定义：一个基于直观或经验构造的算法，在可接受的花费（指计算时间和空间）下给出待解决组合优化问题每一个实例的一个可行解，该可行解与最优解的偏离程度一般不能被预计。

三、基于算法求解实际问题

（一）问题的提出

共享单车动态调度中一个较为重要的环节为单车搬迁路径的选择，即调度车将某个单车过剩的调度点（用车区域）的共享单车运往另一个单车缺少的调度点（放车区域）时，需要择优选择前往路径以确保所花费的调度车使用费用最低。

（二）问题的抽象和说明

调度车每公里的费用固定，因此通过对比从固定位置P的用车区域到K个近邻放车区域的路径长度，选择路径长度最短的近邻放车区域作为终点进行调度。

（三）Dijkstra算法的应用

以一个带有权值的无向图为例，如图2，采用Dijkstra算法作为寻路策略完成对基于起点A到停车区域G的最短路线：

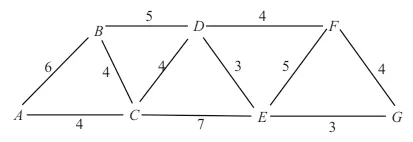
图2 无向图

步骤一： 以带有权值的一个矩阵z表示含有各结点的带权无向图，如图2，矩阵相应位置的数值代表对应线段的权值，如果从一个结点到另一个结点不连通，那么其矩阵中的值为 ∞。

步 骤 二： 选 择 vj，使 S(j)=min{ S(i)| vi∈ {B, C, D, E, F}}，vj是从结点A出发找出一条最短线路的终止结点，令 Q ←Q∪{vj}。

步骤三： 修改起始结点A，再次到集合 {B, C, D, E, F}中任一结点vn之间的最短线路的长度值, 若S(j) + z(j, n) ＜ S(n)，那么S(n) = S(j) + z(j, n)；

基于以上最短距离线路的计算方法, 同时采用欧氏距离计算方法获取基于用车区域当前位置Pcurrent到各停车区域Ci的最短路径path（pathi=Pcurrent→P1→P2→···→Pn→Ci），通过比较两区域之间的线路长度Scost的大小完成路线推荐。对应的公式为：

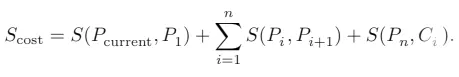
公式中Scost表示用车区域到停车区域的线路长度，S(Pcurrent,P1)表示当前位置Pcurrent到道路交叉口P1的距离，S(Pi,Pi+1)代表边e(Pi,Pi+1)的长度，S(Pn,Ci)代表交叉口Pn到单车分布区域Ci的距离。

（四）哈夫曼树的应用

现构造一个带有权值哈夫曼树，步骤如下：

（1）首先分别赋予四个地铁站（调度点）权值{w1,w2,w3,w4}，每一个权值相当于到达该调度点的时间或距离，构造出4棵只有根节点的二叉树，这4棵二叉树构成一个森林。

（2）在森林当中选取两棵根节点的权值最小的树作为左右子树构造一棵新的二叉树，并置新的二叉树的根节点的权值为其左、右树上的根节点的权值之和，即新的总路径权值等于其分路径权值的加和。

（3）在森林当中删除这两棵树，同时将新得到的二叉树加入森林当中，即将新得到的路径加入路径群中。

（4）迭代，直到森林当中只含有一棵树为止。

四、算法拓展

（一）遗传算法定义

遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程，目前已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。

（二）流程图（见图3）

图3 流程图

（三）在共享单车调度上的运用思路

共享单车的调度受其运营方式的影响，使得其调度过程是一个复杂的动态过程。通常，在对共享单车进行调度分析时，我们把它的调度过程简化成静态过程。本文在建立优化调度模型时，考虑调度的目标函数为如下两个部分：

（1）考虑调度过程中由于调度运输产生的费用。

（2）某个待调度区域共享单车过少或者过剩时由于未被使用带来相应的损失费用。

（四）算法分析

1.初始化调度信息

首先在某区域中的二维坐标随机生成共享单车用户的位置信息以及对应的需求数量，并将该区域均衡地分为25个调度区域，根据用户的需求信息以及调度区域的位置信息，并运用重心法求出每个调度区域的调度站点内，保障每次调度车辆将共享单车调度在该位置可以满足调度需求。最后，初始化各个调度站点的需求数量。

2.调度参数设置

（1）调度站点的距离

在已知各个调度站点坐标的前提下,为了简化问题,本文选取两个调度站点的欧式距离作为两个站点之间的调度距离。

（2）共享单车的调度和损失费用

本文对调度费用做如下假设:针对该区域,共享单车的调度运输费用为12元/公里,而当共享单车不满足用户需求或者是超过用户需求,所带来的损失费用为8元/辆天。

（3）调度车辆信息

本文假定上述划分的25个调度站点(分别命名为1-26号) ,均由该区域的调度中心负责调度,该调度中心包含三辆调度车,每辆车最大装载量为40辆共享单车。

3.调度方案计算

目前,运用遗传算法求解物流配送车辆路径(VRP)问题的研究具有较多成果,运用遗传算法对该优化的调度模型进行求解,求解步骤如下:

（1）参数初始化

初始化样本个数N,最大迭代次数n,交叉概率p和变异概率Pme

（2）种群初始化及编码

本文将调度站点随机连接遍历的路径作为初始化种群,并通过自然编码的方式对该初始化种群进去编码为E(1,2,3,米)

（3）适应度函数

计算本次迭代种群的最优适应值。

（4）迭代

判断是否到达最大迭代次数n,如果到达则退出循环并输出最优的适应值,否则进入(5)。

（5）交叉和变异

选择(4)中个体适应度值小的作为优良的染色体,并按照设置的交叉变异概率进行交叉变异操作,产生新的种群并转入(3)继续计算适应值。

（6）选代终止

到达最大迭代次数,选择最小的适应值作为最优的调度费用,并输出对应的调度路线。

设定遗传算法迭代的参数如下:以模型的目标函数作为迭代的适应度函数,初始化样本为2000个,交叉概率设为0.9，变异概率设为0.12,终止选代次数为600代。

1辆车调度时,站点7、12、19、22、 24未被调度,而其他站点被调度且满足站点的车辆需求,最优的调度费用约为551.19元;当我们使用2辆调度时,其费用为477.14元,其中4、7、10、12、19、21、26这7个站点未被调度,当使用3辆车进行调度且保证都有调度任务时,其调度费用反而增加,最优调度费用为600.78元。分析发现,相比于1辆车和3辆车,派出2辆车时其服务的站点较少,但是节省了调度运输费用,保证了综合成本最小。