基于小波变换和各向异性扩散的红外和可见光图像融合算法

2022-03-14 06:15安倍逸付周兴马瑞泽赵新生

西安科技大学学报 2022年1期

郝帅，安倍逸，付周兴，马瑞泽，赵新生，马旭，刘彬

(1.西安科技大学电气与控制工程学院，陕西西安 710054；2.西安卫星测控中心，陕西西安 710043)

0 引言

图像融合一直是计算机视觉领域中的研究热点，主要是将同一场景中的异源/同源图像按照一定的融合策略生成融合图像，从而增强图像中目标细节表达能力，以便后续处理。目前，图像融合技术已在测绘遥感[1]、人脸识别[2]、医学成像[3]、军事侦察[4]、输电线路故障检测[5]等领域广泛应用。红外图像和可见光图像是图像融合中研究最为广泛的2类图像[6]，红外图像主要是利用目标与背景的热辐射差异来区分目标和背景，它受光照变化以及天气条件影响较小[7]。然而，相比可见光图像，红外图像对目标的细节表达能力往往不足。可见光图像具有较强的细节分辨力，但是它受光照变化影响严重。为此，将红外与可见光图像进行融合，综合二者优点，可以使融合图像能够更加符合人类视觉感知标准，便于后续任务处理。

根据图像表征层次的不同，图像融合可以分为像素级、特征级和决策级融合[8]。决策级融合主要是依据一定的融合准则对每种传感器采集的数据进行可信度综合判断。该方法计算量小，但是由于每种传感器的决策结果都会传递到最终的决策层，所以该方法的融合精度严重依赖于所选取决策函数的容错能力。特征级融合是对各原图像所提取的特征(如形状、边缘、纹理等)进行融合。该方法可以有效降低处理的数据量，计算速度快，但是往往会损失部分细节特征。像素级融合方法是直接在像素点基础上进行融合，该方法可以保留图像中丰富的细节信息，但是处理时存在数据量大且易受噪声干扰等问题。李海宾等在研究中证明了像素级图像融合方法具有较好的融合效果，而且计算复杂度低[9]。为此，本方法研究重点是基于像素级的融合方法。

像素级图像融合方法大致可分为基于空域和基于变换域的融合方法[10]。在基于变换域的图像融合方法中，由于基于多尺度的融合方法模拟了人类视觉系统感知方式，是目前最常用的像素级融合方法之一。刘先红等提出了基于多尺度方向引导滤波和卷积稀疏表示的图像融合方法[11]，陈勇等提出了基于小波变换的融合方法[12]，ZHANG等提出了基于非采样Contourlet变换的融合算法[13]，吴延海等提出了基于NSCT变换和压缩感知的融合算法[14]，他们通过融合实验证明了基于多尺度融合的方法能够获取较好视觉效果。但是叶明等在研究中指出，基于小波变换的融合图像算法会随小波分解尺度的增大出现较为明显的非均匀效应，而且融合结果中会存在细节信息保留不完整问题[15]。

为了使融合结果具有较好的细节表达能力，大量学者利用滤波的方法来增强图像融合效果。如朱浩然等提出了基于迭代导向滤波的图像融合算法[16]，KUMAR采用交叉双边滤波算法进行图像融合[17]，赵程等提出了基于滚动导向滤波和混合多尺度分解的红外与可见光图像融合方法[18]，涂超平等提出了基于各向异性热扩散方程的多聚焦图像融合算法[19]。上述方法的思想都是先将源图像分解为基础层和细节层，然后利用不同的融合策略生成融合图像。封子军等在研究中指出，相比于滤波融合方法，基于各向异性扩散的方法能够更好的保留图像边缘信息，而且图像具有较好的去噪能力[20]。但目前针对各向异性扩散模型提出的改进方式大多都是针对扩散方程本身提出的，忽略了图像的自身特征信息，可能造成图像细节部分(纹理、弱边缘等)的丢失或模糊。

综上所述，为了使融合图像具有较好的细节分辨能力的同时，更加符合人类视觉感知特性，提出一种基于小波变换和各向异性扩散的红外和可见光图像融合算法。

1 小波分解与重构

小波变换作为一种有效的多尺度分析工具，可以将图像分解为低频分量和高频分量[21]。文中利用2个一维滤波器实现对二维图像的快速小波分解，然后通过2个一维重构滤波器实现图像的重构。j-1尺度下的分解公式可以表示为

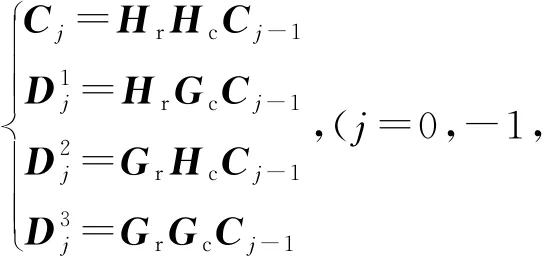
(1)

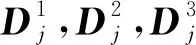
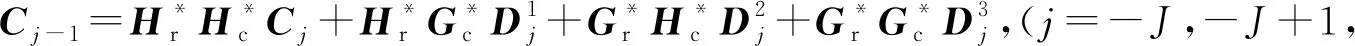
(2)

式中H*和G*为H和G的共轭转置矩阵。

2 各向异性扩散

通过各向异性扩散可将给定的图像保留常规比例下的特性，并借助偏微分方程可以保存边缘轮廓信息，获取区域边界清晰的图像。为此，选择通过各向异性扩散来增强图像的细节表达能力。

各向异性扩散方程可以表示为

It=c(x,y,t)ΔI+c·I

(3)

式中c(x,y,t)为扩散速率；Δ为拉普拉斯算符；为空间变量的梯度算子；t为时间；It为一个随时间t变化的图像。将式(3)利用拉普拉斯算子进行离散化可得到迭代方程

(4)

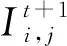
(5)

同理，沿北、南、西、东4个方向上的传导系数可以定义为

(6)

式中 g(·)为使细节平滑与边缘保持之间的一个边缘停止函数。为了使图像具有丰富的细节以及边缘信息，选择函数如下

(7)

式中K为边缘导热系数。

3 融合算法

3.1 融合流程

整个算法的流程如图1所示。

图1 文中算法结构框

1)对源图像分别进行小波变换，提取高频部分和低频部分，在各自尺度进行叠加后形成最终高频层和最终低频层。

2)对上一步叠加生成的低频层和高频层分别进行各向异性扩散从而生成相应的基础层和细节层。

3)细节层融合利用KL变换进行融合，基础层利用加权平均的方法进行融合。

4)将细节层和基础层通过线性融合重构出最终融合图像。

3.2 融合策略

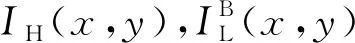
(8)

式中 AD(·)为各项异性扩散运算子。

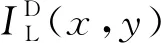
(9)

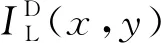
(10)

求取特征值σ1和σ2，并找出其最大特征值σmax，记作

σmax=max(σ1,σ2)

(11)

假定σmax相对应的特征向量为ξmax，由此可计算出融合权重系数KL1，KL2，见式(12)

(12)

(13)

(14)

式中ωn为加权平均系数，且ωn满足条件

(15)

实验中，取ω1=ω2=0.5。

3.3 线性融合重构

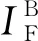
(16)

部分融合结果如图2所示。

图2 融合结果图像

4 仿真结果及分析

为了验证所提出融合算法(WDK)的优势，选取多尺度奇异值分解(MSVD)算法、小波变换(WT)、双尺度融合(TS)算法进行比较，从主观和客观2个方面来对算法的性能进行评估。本算法的运行环境为戴尔笔记本电脑(型号为灵越7380)，软件平台为MATLAB R2019a，所用的异源图像来自于数据库https：//figshare.com/articles/TN_Image_Fusion_Dataset/1008029。

4.1 主观评价

为了验证本算法的主观评价效果，从上述数据库中随机选取5组经过配准的红外与可见光图像进行融合实验，各算法的融合结果如图3所示。

从图3第1组图像可以看出，图3(d)(f)背景细节和房屋边缘对比度不高，融合结果较为模糊，图3(e)图像对比度较高，但房屋边缘及背景信息保留不完整，而本算法图3(c)可以明显看出房屋边缘纹理较为清晰，如图中红色矩形框区域所示。从图3第2组图像可以看出，图3(d)(e)(f)背景信息较为模糊，本算法图3(c)具有较高的图像对比度，在红色矩形框标注的部分可以清晰的看到人的边缘轮廓信息，融合效果较好。从图3第3组图像可以看出，本算法相比于其它算法更好地保留了树木细节信息。从第4组图像可以看出，图3(d)(e)图像清晰度较低，图3(c)和(f)的图像清晰度较高，但是图3(c)中红色矩形框中所示的树木细节信息相比于图3(f)更加丰富。而在第5组中，4种方法的融合图像都能将烟雾中的人物较为清楚的表示出来，但本算法能够更好地保留源图像的人物边缘轮廓，融合效果较好。通过以上5组对比实验可以看出，相比于其他3种融合算法，本算法能够更好的保留融合图像中目标的细节信息。

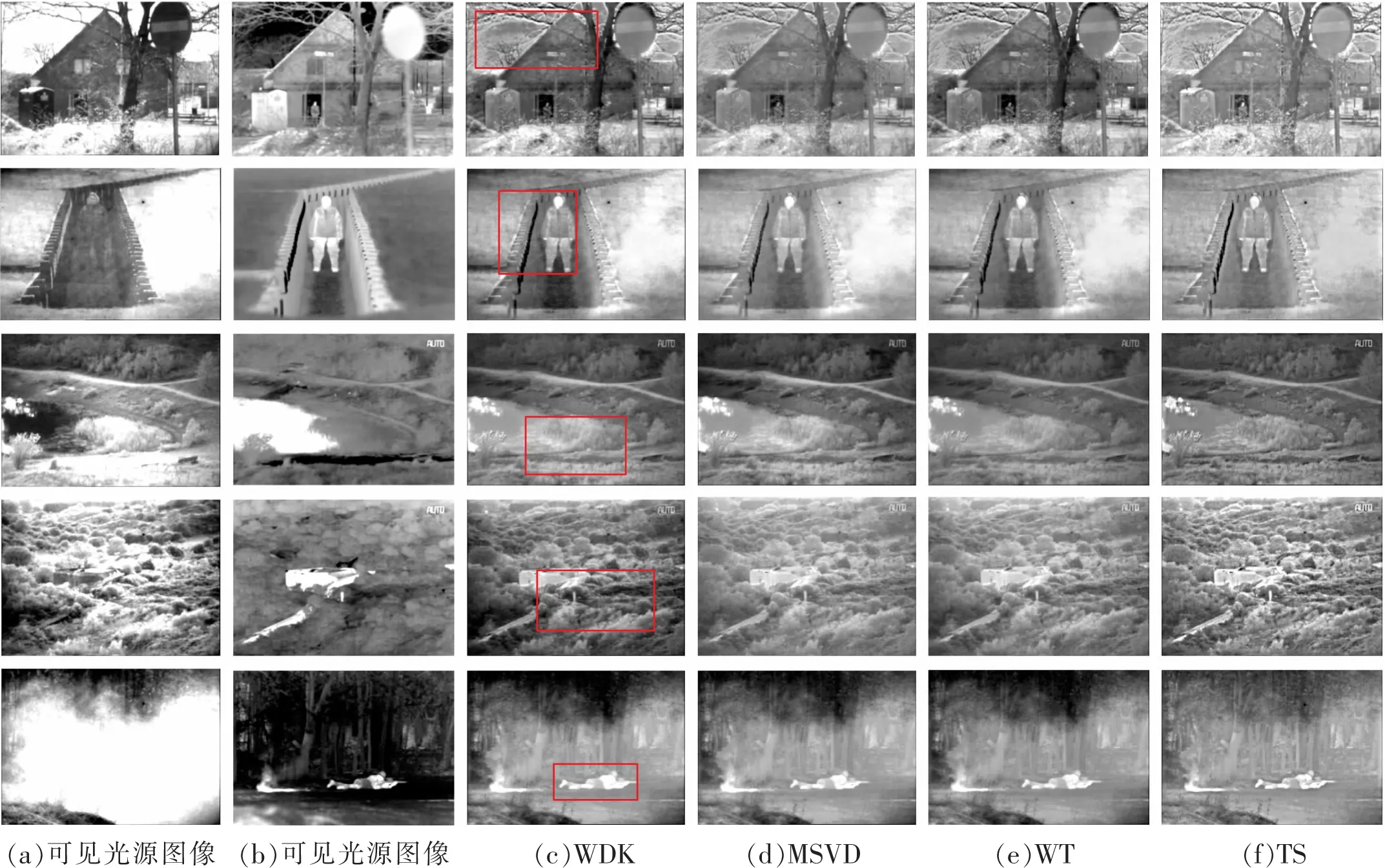
图3 图像融合结果比较

4.2 客观评价

为了客观评价本算法的优越性，实验中选取香农熵(shannon entropy，EN)、图像交叉熵(cross entropy，CE)、特征相似度(feature SIMilarity，FSIM)、图像互信息(mutual information，MI)、相对标准偏差(relative standard deviation，RSD)以及运行时间作为评价指标[23]。其中，EN反映图像所含信息量的丰富程度，数值越大表明获得的融合图像所包含的信息量越大；CE表示融合后2幅图像与原始图像的交叉熵。交叉熵越小，图像间的差异越小，融合效果越好；FSIM用于评价图像间相似度，数值越大说明融合图像与源图像在某些特征方面更相似；RSD表示原始图像与融合图像的相对标准偏差，反映了与真实值的偏差程度，相对标准偏差越小，融合精度越高，图像融合效果越好；MI表示融合后的图像与原始图像之间的相互信息，MI越大，2幅图像的相似度越高。

利用4.1节主观评价中的5组图像进行测试验证，其客观评价指标结果分别见表1～表5。从表1～表5可以看出，所提出算法的EN值在4组实验中效果最好，FSIM值在2组实验中保持数值最优，其余3组均为次优值，说明所提出的算法可以较好的保留源图像的信息，而且融合后的图像与原始图像特征具有较高的相似度。通过5组对比实验的CE数值可以看出，所提出算法生成的融合图像与源图像差异较小。通过5组实验的RSD指标可以看出，本算法在其中4组对比实验中效果最好。通过5组对比实验的MI指标可以看出，本算法均为最优数值，表明本算法相较于其他算法，融合图像的特征相似度与原始图像最为接近。从各算法的运行时间可以看出，所提出算法和TS算法的实时较好，其运行时间远小于其他算法，可以用于对实时性要求较高的场合。通过各客观评价指标可以看出，所提出的算法综合性能最好。