毛竹管桩基坑支护可靠性研究

邓友生，付云博，叶建军，彭程谱，李令涛

(1.西安科技大学 桩承结构研究中心，陕西 西安 710054；2.湖北工业大学 土木建筑与环境学院，湖北 武汉 430068)

0 引 言

支护桩以良好的抵抗变形能力广泛用于基坑建设中，完善的技术与高适应性保证工程支护的稳定性[1-2]。传统混凝土桩用于支护有施工周期长、成本较大等缺点，倘若不满足工程需要，容易产生工程事故[3-4]。尤在土质条件复杂时，基坑事故发生频率最高，支护桩使用功能直接影响基坑稳定性[5]。

可靠度是评价支护桩使用功能的重要指标[6]。桩基工程中对可靠度的研究已取得了一些成果，JIANG等采用响应面法对倾斜场地横向受荷桩可靠度分析桩顶位移变异性与荷载的关系[7]。MANISH等以最小二乘法和高斯回归建立群桩支护可靠度指标公式对比一次二阶矩法，新方法有更强的适应性[8]。边晓亚等以桩基长径比、容许沉降和沉降控制条件为影响因素，利用均值一次二阶矩法计算群桩可靠度指标[9]。陈飞等针对离子型稀土矿山滑坡问题，以竹桩为主进行生态护坡，有效提高了边坡稳定性[10]。基于Copula理论，唐小松等考虑参数不确定性提出基桩荷载—位移双曲线概率分布方法[11]；辛军霞等针对土体参数离散型过大问题，改进了CFG桩复合地基的可靠性评估[12]。邓友生等使用竹桩对基坑进行支护试验，利用有限差分法对比分析，基坑支护中使用毛竹管桩具有较好效果，表明环保支护体系的可行性[13-14]。戴自航等针对毛竹复合土钉墙支护变形预测与控制方面，建立有限元模型，分析认为竹桩长度对坡体水平位移影响较明显[15]。JANUSZ等采用近似响应面法建立加载桩极限状态函数，对嵌入垂直裂缝的非饱和基底单桩进行可靠性评价，结果与饱和度最相关[16]。郝腾结合JC法与一般分离法研究螺旋桩复合地基可靠度，结果表明桩端阻力变异系数和地基承载力折减系数对可靠指标影响较大[17]。JIANG等考虑土体参数的分布状态，分析各参数对边坡可靠指标的影响[18]。

目前多以极限状态下最大荷载为失效准则，对承载桩进行可靠性评估。但在桩基受荷未达到极限承载力却已经不满足工程安全性需求时，计算的可靠度指标无法体现正常使用状态下支护桩使用功能，导致工程事故频发。毛竹管桩具有较好的承载能力，属绿色建材，可有效降低能耗，绿色无污染符合可持续发展战略，对毛竹管桩应用于基坑支护进行可靠性分析，为推进工程化提供理论基础。针对此问题，引入中心点法分别以桩顶容许位移、计算位移和极限与容许位移比为基本影响因素，分析毛竹管支护桩正常使用极限状态和承载能力极限状态下各参数对可靠度指标的影响规律。

1 模型因子及变量

不确定因素对不同组桩顶位移数据的影响使无法直接进行可靠性对比，同种因素下难以收集足够的数量进行统计，为增大样本容量，消除不同组桩顶位移差异性，引入竹桩桩顶位移试计比λ

(1)

式中dm和dp分别为支护桩桩顶实测位移和计算位移。

防止基坑变形失控状态发生，应在支护承载接近极限变形处设置警戒值。变形触动警戒值应及时补强支护体系。警戒值设定应接近极限变形，并保证在基坑发生失稳前留足够的反应时间[19]。受土质条件、施工方法等因素的影响，差异性无法定量分析，故设桩顶位移容许值为警戒值，表示为dtol，采用极限状态方程建立功能函数Z

Z(dm)=dtol-dm

(2)

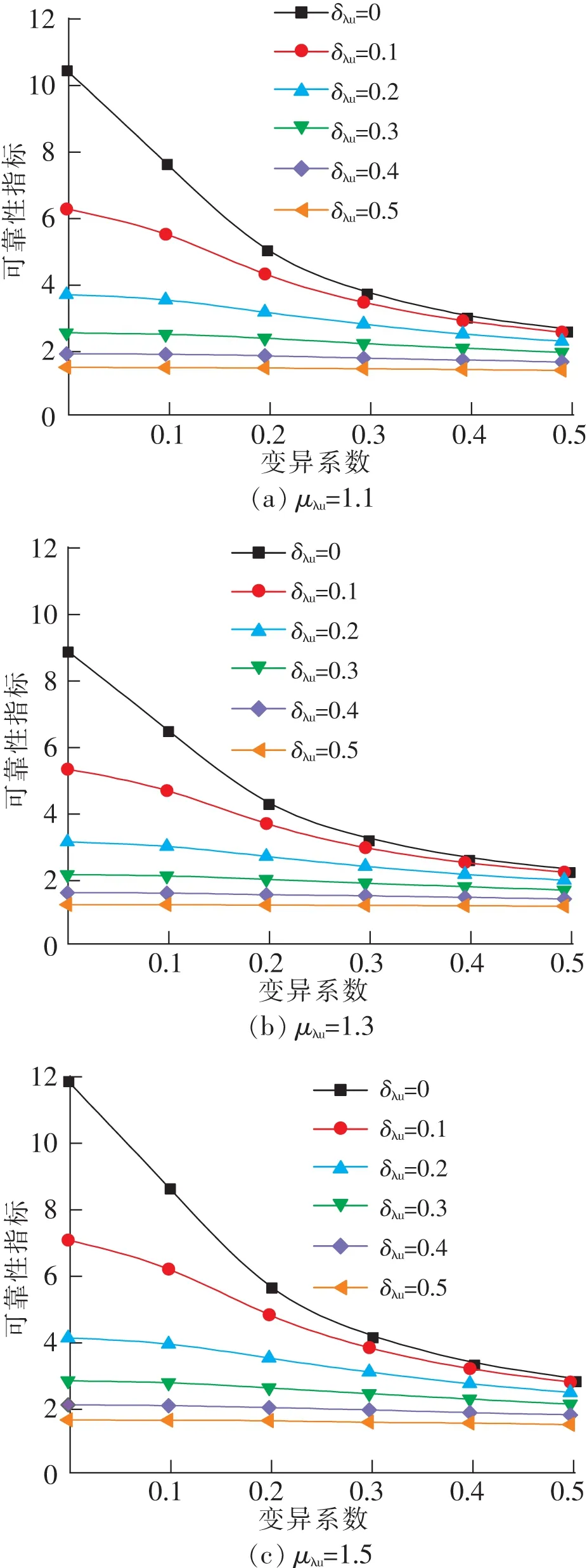
当Z=0时，表示竹桩支护能力在临界状态；当Z<0，即dtol

P=Pr(dtol

(3)

支护桩可靠度设计常引用安全系数K，定义为容许位移与计算位移的比值

(4)

式中μdtol为容许位移平均值；μdp为计算位移的平均值。

文献[20]中桩基理论分析时，安全系数K取3.5，试验设计时，K取值2.0。竹桩为天然毛竹制作而成，强度较混凝土略显不足。设安全系数取2.0，2.5，3.0，3.5，利用中心点法分别计算得可靠性指标为2.16，3.00，3.69，4.28。当可靠度在2.5～3.5之间时，安全级别属于中等。因此，为满足正常使用极限状态与承载能力极限状态下可靠性及经济性要求，安全系数取2.5。

在对支护桩进行可靠度分析时，应检验相关变量的分布特性，桩顶位移是重要的基本统计参数。程志和进行了分步开挖、加载过程下直排与齿状毛竹管桩对基坑支护作用的足尺模型试验[21]，支护结构体系如图1所示。利用上述计算方法和收集的实测数据，计算支护桩的位移和试计比(表1)。

图1 基坑支护结构体系

表1 桩顶位移偏差统计

在同为黏性土、毛竹管桩和静压加载条件下，2种布桩方式的λ差别不大，但λ的变异系数有较大差异，两者相差0.06，齿状排桩λ的变异系数较小，是直排桩支护体系的46%。试验中直排桩桩顶前缘出现略微土块脱落，齿状排桩支护下基坑侧壁未出现明显变形，桩顶位移整体小于直排桩。表明齿状排桩较直排桩能更好地支护基坑变形，减小桩顶位移的变异性。

采用Kolmogorov-Smirnov(简称K-S)检验法和Anderson-Darling(简称A-D)检验法，显著性水平取0.05，分析在正态分布、对数正态分布和极值Ⅰ型分布下，桩顶位移偏差统计量的统计特性。由K-S检验和A-D检验结果(表2)得到试计比的统计值均小于临界值，表明2种检验法对假定的3种分布均接受。对数正态分布统计值为0.15和0.23，3种分布中为最小值，样本更收敛。

表2 试计比统计检验结果

2 正常使用极限状态

根据中心点法，依据对数正态分布对基本变量进行设计计算，可靠度指标β

(5)

式中μZ为功能函数Z的均值；σZ为功能函数Z标准差。

BIAN等对受荷桩两种极限状态下的可靠指标进行了线性分析[22]。借鉴此线性关系，在正常使用状态下，λ，dtol和dm服从对数正态分布。结合中心点法，竹桩支护失效概率及可靠度指标βsls

pfs=P(dtol

(6)

为考虑成桩方式在支护桩可靠度分析中的影响，以计算位移变异系数(δdp)与容许位移变异系数(δdtol)为基本变量，取值范围0～0.5，对毛竹管支护桩进行可靠度计算。由图2(a)，βsls随着δdp从0递增到0.5呈现明显的下降趋势，曲线则表现得愈加平缓，表明βsls值随δdp的增大而减小，即计算位移变异系数的增大使得支护桩可靠性降低，但影响幅度逐渐减弱；δdtol从0至0.5所对应图2(a)中的6条曲线整体依次降低，δdtol为0时βsls曲线整体最大且最为陡峭，最大值为11.07，最小值为1.46，陡峭程度随δdtol的增大而降低，表明dtol的不确定性愈大，支护桩的可靠性越低。

依据小概率事件，失效概率5%，可靠指标大于1.65，判定支护能力满足安全要求[23]。图2(a)中，当δdtol=0.5时全部不符合安全要求，δdtol=0则全部满足。δdtol=0.4时，δdp=0.2的可靠指标βsls为1.72虽然满足要求，但其仅高于判别值0.07，风险较大。因此对支护桩进行可靠性分析时，相较于计算位移更要充分考虑容许位移的不确定性。

图2 正常使用极限状态下变异系数与可靠性指标关系

齿状排桩与直排桩支护下βsls的变化情况类似，表明齿状与直排两种布桩方式在δdp与δdtol影响因素下支护桩可靠性趋势并无明显区别。两种布桩方式下βsls的差值较小，且齿状排桩支护下βsls略大。但在忽略计算位移与容许位移的影响时，即δdp与δdtol都为0，直排桩支护下βsls=6.54，是齿状布桩方式下的60%。

齿状布桩方式提高了可靠度评价结果。其原因在于齿状排桩支护设计对桩顶位移有一定的抑制作用，对基坑的支护更加稳定，致使λ的变异系数较低，有效减少了桩顶位移试计比的变异性，提高了可靠性。

3 承载能力极限状态

以桩顶容许位移与计算位移为基本变量的可靠度计算方程，属正常使用极限状态下稳定性设计。实际桩顶位移触及警戒值时，整体支护结构未失效但未达到预期效果，在进行补强加固同时，相对于βsls，更需可靠度设计计算此极限状态下的指标βuls。

支护体系稳定性分析中，极限状态下的容许位移并不能完整映像基坑支护可靠度。依据不稳定因素影响，引入极限位移与容许位移的无量纲试计比(λu)，较传统承载能力极限状态可靠度设计，具有更高安全性、准确性。以下可靠指标设计时取λu作为主要变量，分析极限与容许位移比均值μλu及其变异系数δλu(0～0.5)、δdp(0～0.5)与βuls的关系。将收集的两组试验数据综合处理，正常使用极限状态试计比均值μλ为1.095，变异系数δλ为0.11(表3)。

表3 极限与容许位移比的变异系数对可靠性指标的计算结果

δλu和δdp以相同值变化，δλu随βuls呈变化增大趋势，因此δλu对βuls的影响高于δdp，变化率随变异系数递变而增大：将δλu=0,δdp=0，βuls=10.45设为定值组，当δλu和δdp分别取值0.5时，极限与容许位移比的βuls结果为1.29，计算位移变异系数的βuls为2.49，较定值组，二者的可靠指标变化值相差1.20。承载能力极限状态下的可靠性设计中，极限位移与容许位移比的判定尤为关键。

随着δλu和δdp递变，βuls变化趋势在0.2处转变。变量小于0.2时，βuls值随变异系数的增大而加速减少，曲线较大于0.2时更加陡峭。表明可靠性指标随变量的增加呈先加速下降，经0.2后下降衰减趋势。变量δλu和δdp对可靠度指标影响整体趋势呈持续减弱。

考虑λu的变化，在研究极限承载能力对竹桩支护能力可靠度指标的作用时，将其分为三类讨论(μλu取1.1，1.3，1.5)，分别计算可靠度指标，以探讨在承载能力极限状态下对支护竹桩可靠度指标的作用。

比较图3不同极限与容许位移比下可靠性指标，随着μλu的增大βuls逐渐增大。当δdp和δλu不断增加时，不同极限位移与容许位移比的均值之间βuls差值开始缩小，且βuls的减少速率快于μλu增大速率。表明δdp对βuls的影响较为显著，且影响程度大于μλu。因此，有效抑制干扰设计位移，降低变异性是提高支护体系可靠性的主要因素。

图3 承载能力极限状态下变异系数与可靠性指标关系

以安全级别不低于中等，即βuls≥2.5为目标可靠度[24-25]。当δλu=0.3时，μλu=1.1条件下的βuls全部不满足目标可靠度，而μλu=1.5时，δdp=0.1下βuls=2.63满足目标可靠度。在设计时先确定目标可靠度，然后根据现场土质情况等来设计并计算出极限与容许位移比。而土质参数和施工条件往往具有较大误差，难以精确控制，此时需要提高极限预估量，即增大极限位移与容许位移比来满足工程稳定性。

4 结 论

1)毛竹管桩桩顶位移承载能力极限状态可靠度指标可由正常使用极限状态可靠度指标线性表达。

2)桩顶容许位移与计算位移的变异系数对支护桩βuls呈负相关，在低变异性下影响较为显著，转折点为0.2；对支护桩进行可靠性分析时，相较于计算位移更要充分考虑容许位移的不确定性。

3)在正常使用极限状态下，齿状排桩较直排桩有更优的可靠度，随着桩顶计算位移与容许位移的变异性增加，二者可靠度指标差异性逐渐减小。

4)毛竹管桩βuls随μλu不确定性的增大而减少，随μλu的增加而变大。桩顶设计位移定量时，为满足目标可靠度，可适当提高极限位移与容许位移比或降低其变异性来满足需要。