煤矿输煤栈桥抗振性能及动力响应

谷拴成，姚博语，任 翔，王 劲

(1.西安科技大学 建筑与土木工程学院，陕西 西安 710054；2.长庆油田西安长庆科技工程有限责任公司，陕西 西安 710018)

0 引 言

钢桁架输煤栈桥是带式输送机的重要承重构件，是煤炭、电力、冶金等产业中十分关键的连接通道，在生产流程中扮演着十分重要的角色[1-3]。结构有跨度大、刚度小及倾斜角大的不利因素，存在结构的质量和刚度沿竖向分布不均匀，薄弱点多，安全、稳定问题突出[4-5]。近年来，钢桁架输煤栈桥事故频出，如果钢桁架输煤栈桥结构发生破坏，将导致煤矿生产链陷入瘫痪，带来很大的经济损失，因此确保输煤栈桥的安全和稳定是十分重要且具有研究价值的[6-8]。

国内外学者对桥梁的研究主要集中于结构动力的方面，SIMON等提出通过优化腹杆体系及钢桁架布置方式可以提高输煤栈桥整体刚度的研究方法。[9-11]。张月强等主要研究大跨度钢结构桥梁以及大跨度斜拉桥，提出了等效荷载瞬时卸载法以及三个阶段控制的理论[12-13]。CASADO、张建伟等针对大跨度斜拉桥的抗振性能进行了详细的分析，并描述了在多方向激励下，斜拉桥的振动响应，分析了其抗振性能的研究方法[14-15]。沈星等对机械振动下超大跨度桥梁的抗振性能与振动控制进行研究，提出了具体的抗振方式[16-18]。倪永军等对比国内外大跨度桥梁的抗振设计规范，为大跨度桥梁的抗振设计提供参考依据[19-21]。李强等对钢桁架桥梁结构的动力特性进行了有效识别，用有限元软件建立了该桥梁结构的数值模型，分析整体结构在荷载激励条件下的动力响应，对现场数据和数值结果进行对比[22-23]。以上文献仅限于桥梁结构的抗震分析，考虑的相关因素不多，且输煤栈桥结构相对于一般桥梁结构有其独有的特点，针对这一特殊结构的研究相对较少。

结合输煤栈桥，建立有限元分析模型，计算分析栈桥动力特性，并将有限元计算结果与现场实测值进行对比分析，验证有限元计算正确性，揭示输煤栈桥动力特性，为今后煤矿输煤栈桥的设计提供了理论依据。

1 皮带输煤栈桥动力特性

1.1 输煤栈桥动态响应机理

栈桥振动主要是由两种不同的激励方式引起的，分别为：①物料在皮带上的不规则运动所产生的冲击荷载；②皮带下的托辊在高速转动过程中产生的间歇激励。这两种荷载确定的难度非常大[24]，动荷载和动荷载产生的动力响应之间存在着线性关系，简支梁桥在外荷载f(x，t)作用下的运动方程可表示为

(1)

式中EI为简支梁抗弯刚度；m为单位长度质量；c为阻尼系数；u(x，t)为简支梁竖向位移。

若外荷载为长度为Lt的匀速移动均布荷载p，则f(x，t)可表示为

f(x,t)=-p·[H(x-vt+Lt)-H(x-vt)·

(2)

式中v为荷载速度；Lb为简支梁跨度；H为Heaviside函数。公式(2)等号右边的前半部分反映作用于简支梁上荷载的空间属性；后半部分则反映了作用于简支梁上荷载的时间性质，移动荷载从到达简支梁时由H(t)开始，离开简支梁时引入H(t-(Lt+Lb)/v)。

1.2 钢桁架输煤栈桥动力分析有限元方程

采用有限元软件分析模块的动力算法模拟，表达式为

(3)

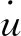
(4)

式中 [M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；[P]为节点荷载向量[25]。

2 输煤栈桥

2.1 栈桥结构

钢桁架输煤栈桥内部结构采用工字型钢或双角钢作为上部结构主要受力杆件；两个侧面由上、下弦、竖向和斜向腹杆组成。为确保钢桁架栈桥有充足的操作空间和人行通道，用桁架的端竖杆与檩条在结构上部组成门型刚架，角部设置隅撑进一步提高刚度。栈桥顶部及两侧则采用压型钢板封闭，形成封闭的空间体系。

图1 移动均布荷载通过简支梁桥

图2 输煤栈桥内外部结构

2.2 栈桥监测

2.2.1 选择监测桥跨结构原则

钢桁架输煤栈桥结构下部的桥墩对整体结构起着关键作用，桥墩越高，整体结构就更柔，当输煤栈桥在正常工作时所产生的振动就越大，由此产生的响应相较于桥墩较低的结构均比较大；输煤栈桥结构所处的地形对结构振动也有很大影响，当地形坡度较大时，桁架结构除自身振动以外，竖向振动也会随之增大；作为输煤栈桥的连接处，当输煤栈桥运送的物料到达转载点处时，物料产生的冲击荷载相比于距离转载点较远位置的荷载大很多。

2.2.2 监测桥跨结构的选择

考虑到现场实际及长期监测的可行性，除四段外其余三段均由段中展开布置监测点，全桥共计19跨作为安全监测的对象。

2.2.3 监测点布置

基于主要结构的动力测试，监测桥跨仅给出动力特性监测测点布置，结构应力监测不给出。动力监测测点布置在跨中位置，可监测三向振动情况(图3)。

图3 传感器布置图

3 栈桥动力特性

3.1 有限元模型

输煤栈桥采用钢桁架体系，桁架跨度为30 m，桁架高度为3.5 m，主桁架采用斜腹杆进行支撑，桁架两侧设置斜腹杆，桁架的上下弦杆与两侧桁架刚接，框架柱与框架梁的混凝土等级为C35，钢筋为HRB335，钢材为Q345B，结构安全等级为二级，设计使用年限为50 a，场地类别为Ⅱ，抗震设防烈度为6度。

栈桥钢桁架主要使用双角钢及工字钢，由于其结构特殊性，上弦杆和下弦杆的钢结构杆件布置形式相同，但由于荷载主要由下弦杆支撑，杆件横截面尺寸大于上弦杆(表2、图4～图6)。

表1 材料属性

图4 目标栈桥截面及杆件布置

图5 上弦支撑截面及杆件布置

图6 下弦支撑截面及杆件布置

表2 构件截面特性表

3.2 模型化简原则

为了满足结构受力的实际情况，对结构的计算模型进行简化。

目标结构分析的主要结构成分包括结构体系、节点、荷载、主要杆件。将杆件视为轴线，并以节点间距计算，荷载直接作用于轴线之上，不考虑偏心影响；建立模型时忽略对整体结构影响较小的屋面、输煤皮带等构件，荷载以恒荷载及活荷载的形式传递至计算模型。

3.3 荷载条件

除去结构自重荷载，其他的恒载及活载等均等效为均布荷载施加在桁架结构的上弦杆及下弦杆上。施加在桁架结构上部的均布恒载为0.5 kN/m，均布活载1.9 kN/m，桁架结构下部施加的均布恒载为4.9 kN/m，均布活载5 kN/m。施加移动荷载为60kN/m，运行速度2.5 m/s。

根据上述化简原则与荷载条件，建立单跨有限元计算模型(图7)。

图7 栈桥有限元计算模型

3.4 模态分析

3.4.1 模态提取方法

为达到结构规范[26]要求，对所得所有数据进行了质量参与系数及累计值的判定方法。若考虑结构所有振型，则各方向质量参与系数之和为100%。通过检查所有振型中横、纵、竖向各阶质量参与系数之和，由此判断是否满足规范要求。由横、纵、竖3个方向的质量参与系数，能够判断出目标结构每一阶振型的形式。

3.4.2 结构动力特性

采取特征向量法对目标模型进行分析，得出前30阶振型与频率。在提取模型前10阶振型信息后，得到以下结果(表3)。

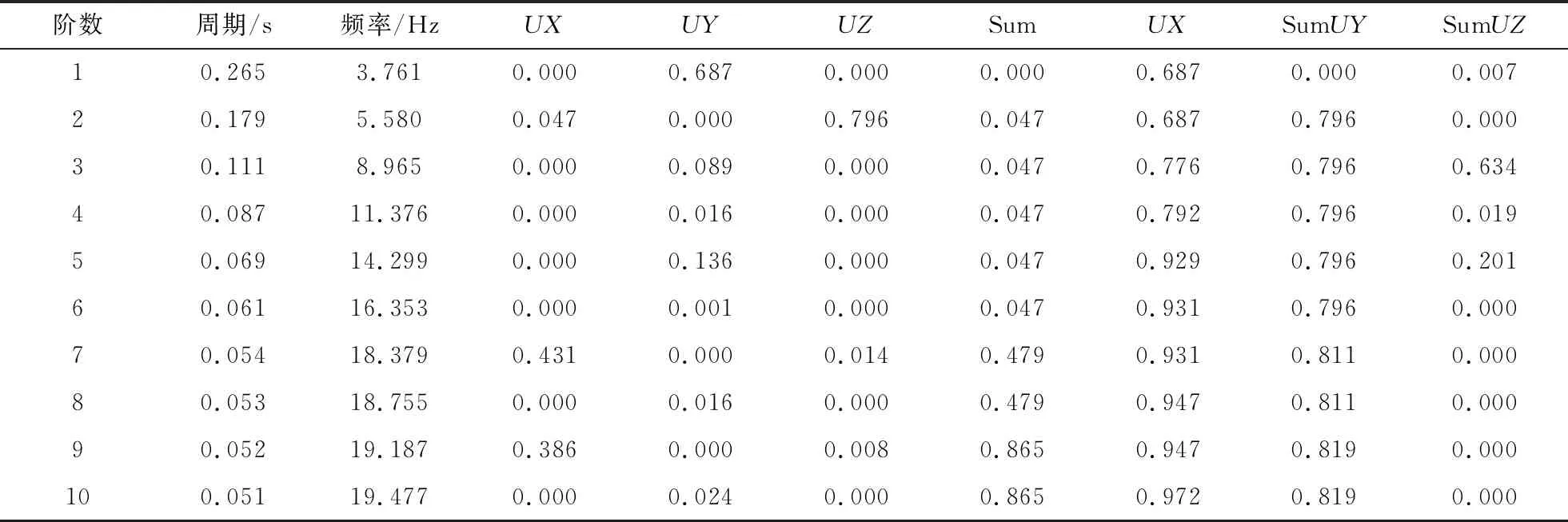
表3 栈桥钢桁架前10阶模态参数

由表3可得，目标栈桥前3阶振动频率分别为3.76，5.58和8.97 Hz，根据参数判定规则，一阶振型为横向平动，三阶振型为竖向弯曲，五阶振型为不规则扭转(图8)。

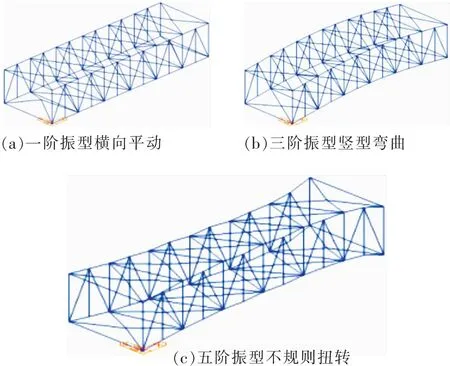
图8 钢桁架振型图

目标栈桥结构节点编号如图8、图9所示。考虑结构最不利荷载位置，选取具有代表性的跨中(35)及四分点(29、41)作为控制点，分别分析栈桥结构在负载工况下及空载工况下的位移与加速度响应(图10、图11)。

图9 各节点编号

图10 负载工况竖向振动位移曲线

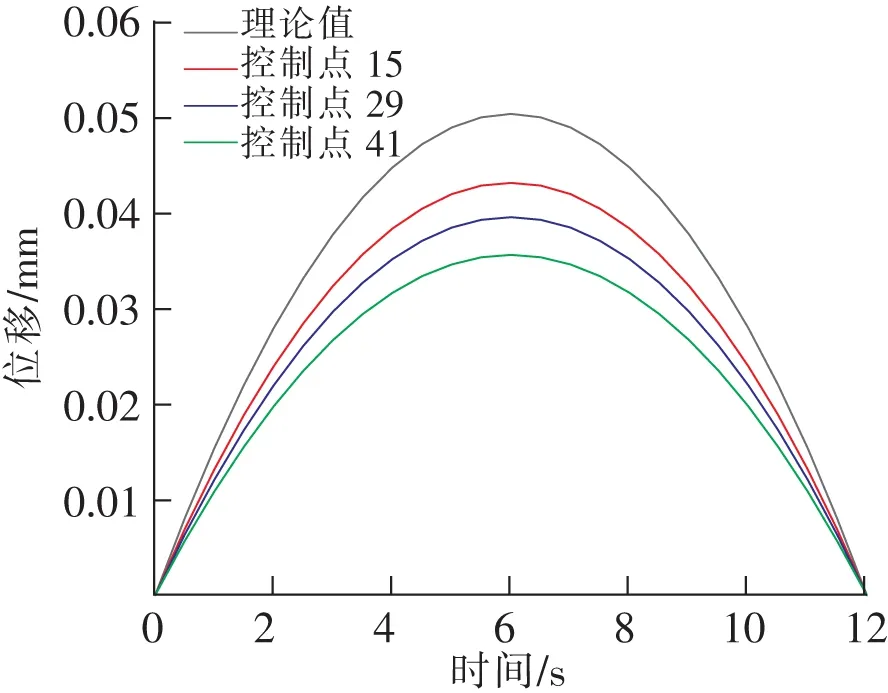
图11 空载工况竖向振动位移曲线

在动荷载作用下，3个分析控制点的动力响应变化趋势基本一致；在空载及负载工况下，跨中节点的位移响应及加速度响应最大。负载工况下，跨中竖向位移最大为0.368 mm；空载工况下跨中节点竖向位移最大为0.049 mm。负载工况下竖向位移是空载下的7.8倍。说明负载运行时输煤栈桥的动力放大效应要比普通梁桥大很多，如果按照传统公路桥梁的设计方法进行设计，不能满足输煤栈桥安全生产的要求。

3.5 频域分析

目标栈桥皮带在正常运行时激振频率为7.16 Hz，但在实际工况中机器振动频率难免有所波动。由于上述情况，将本模型求解频率范围设为0～15 Hz(图12)。

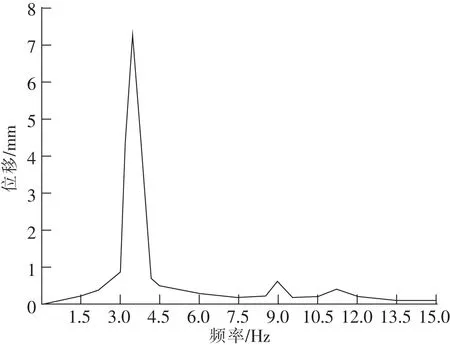
图12 控制点位移响应曲线

通过分析图12所示曲线可知结构动力响应有3个明显区域。结构在振动频率为2.5～4.3 Hz时位移与加速度响应比较大，应为第1共振区，当振动频率为3.4 Hz时响应达到最大值；结构在频率段为8.5～9.9 Hz范围内，结构同样有较大响应，为第2共振区；结构在频率段为11.1～12.3 Hz时为第3个共振区，相较前2个共振区，结构位移及加速度相应相对较小。由上述分析可以看出第2共振区相较第1共振区相应较小，且第2共振区的振动频率范围处于正常工作振动频率范围之外。当输煤栈桥处于加速至正常工作状态或减速至静止状态的过程中，尽量避免振动频率处于第1共振区范围内，特别是3.4 Hz左右。

3.6 结果对比

为验证数值计算结果，将实测数据与数值模拟数据进行对比，对比数据均取其最不利位置的最大数据，基于现场实测的最大竖向位移为0.354 mm，通过数值计算的最大竖向位移为0.368 mm，两者比值为0.96，数值解接近实测值，表明数值模型基本正确，可以作为参考依据。

表4 实测值与计算值对比

4 结 论

1)目标输煤栈桥前3阶振动频率分别为3.76，5.58和8.97 Hz，结构一阶振型为横向平动变形，二阶振型为竖向弯曲变形，三阶振型为竖向弯曲变形。

2)时程分析中简化栈桥动力荷载，对目标栈桥结构动力响应进行分析，目标结构跨中竖向位移最大值为0.368 mm。

3)频域分析中，当输煤皮带处于加速或减速过程时，避免结构振动频率与第1共振区频率相同，防止结构振动响应过大而产生破坏。