固定单站测向交叉无源定位：从光波到微波的应用演进∗

石 荣 陈俊豪 马 达

（电子信息控制重点实验室 成都 610036）

1 引言

单站无源定位是电子对抗侦察的重要应用方向之一，在电磁目标情报获取中发挥着关键作用［1～2］。按照侦察站的运动状态分为运动单站定位与固定单站定位两大类。在侦察站能够主动控制自身运动方式与运动状态的情况下，运动单站无源定位能够获得更多更好的观测条件与测量数据，模型构建与定位解算相对清晰，而且还可以从多站定位的视角来进行理解，很早就有大量文献对其进行过比较全面的归纳总结［3～4］。而对于固定侦察站来讲，除了能够对电磁目标的信号来波方向进行实时测量之外，还面临着定位过程是否具备可观测性和求解奇异性等问题。为此，固定单站无源定位又细分为两种：附加运动目标观测条件的定位和非附加运动目标观测条件的定位。前一种要求被定位的辐射源目标一定是一个运动目标，并且目标在被定位期间不能连续做较大机动，最好是做匀速直线运动，而且与运动相关的某个物理量能够被间接推算或直接测量，例如：实时测量运动目标的径向速度，或是辐射源目标信号的多普勒频移变化等参数，在此基础上还要求目标的运动方向不能在与侦察站的连线方向上，所以应用条件相对受限。而后一种不需要预先强制附加目标的任何运动约束条件，只要目标对外辐射电磁信号，无论其是否运动，也无论其做何种快速机动，都能够立即对其实施定位，具有定位速度快、适应目标范围广等特点，这就是本文所关注的固定单站测向交叉无源定位。

目前还没有文献对此类无源定位体制进行过全面的归纳总结，所以本文分别针对单条测向线与位置约束面交叉定位、以及多条测向线相互交叉定位这两类固定单站测向交叉无源定位方法，从定位模型、解算条件、典型示例等角度阐述了其从光波到微波的应用演进过程，对比分析了不同频段不同方法之间的应用特点与紧密关联，揭示了高精度干涉仪测向在微波频段的固定单站测向交叉无源定位中所发挥的核心关键作用，并对其未来发展趋势进行了分析与展望。

2 测向线与约束面交叉的无源定位

侦察方所掌握的先验知识如果显示被定位的目标位于空间中某一确定曲面上，我们称之为约束面，那么只要能对目标信号的来波方向进行测向，则该测向线与约束面相交的交点处便是目标所在位置。

2.1 光波频段的应用

人眼本质上是一种光学系统，也具备粗略的光信号测向功能，但在光波频段更精密的对目标自身发射或反射的光信号进行测向的主要设备是各种光学仪器与望远镜。这类通过测向来实现固定单站定位的数学模型如下：记空间中固定侦察站的位置坐标为(x0,y0,z0)，侦察站测向所获得的目标来波方向线的单位方向矢量为(γx,γy,γz)，测向线用一个直线方程表示，目标所在的约束面用一个三维函数g(xT,yT,zT)=g0表示，于是通过如下联立方程组求解即可获得目标的位置坐标(xT,yT,zT)。

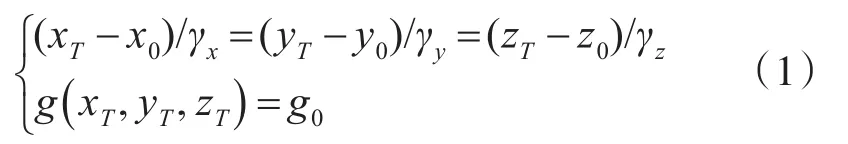
在现代高技术战争中世界各国均采用同步静止轨道的导弹预警侦察卫星对弹道导弹的点火发射点进行红外成像定位，例如美国的国防支援计划DSP（Defense Support Plan）卫星系统和天基红外预警卫星系统 SBIRS（Space-based Infrared System）［5］，俄罗斯的US-KS导弹预警卫星与新一代“统一太空系统”导弹预警卫星［6］。在这些应用中同步静止轨道的预警侦察卫星作为位置已知的固定侦察站通过光学望远镜对位于地球表面发射点处的导弹尾焰光信号进行成像，获取其来波方向，通过测向线与地球表面相交来解算导弹发射点的位置坐标，从而完成固定单站定位。

2.2 微波频段的应用

在光波频段的固定单站定位应用示范的牵引下，微波频段的这一定位体制也开始推广运用。例如：针对飞机上敌我识别器IFF（Identification Friend or Foe）的应答信号特点，从截获的IFF信号中解译出高度信息，从而形成一个瞬时的高度约束平面，地面固定单站对IFF信号进行测向，则来波方向线与上述高度约束平面的交点处便是IFF应答器所在的位置［7］。同样在航天电子侦察系统中也沿用了各种导弹预警侦察卫星中光波频段的单站无源定位方法。首先同步静止轨道电子侦察卫星采用干涉仪对地基和海基的各型雷达与通信终端等电磁辐射源信号的来波方向进行测向［8］，再加上这些辐射源均位于地球表面上，这一约束面在精度要求不高的情况下可近似为一个椭球面，在精度要求较高的情况下可采用三维数字地球数据来精细构建，总之这一约束面和电子侦察卫星的位置事先完全已知，于是测向线与地球表面相交的交点处便是电磁辐射源所在位置。这也反映了测向线与约束面交叉的固定单站无源定位体制从光波频段向微波频段的自然演进过程。

3 测向线相互交叉的无源定位

除了前一小节所述方法之外，测向线相互交叉是另一种非预先强制附加运动目标观测条件的固定单站无源定位方法。从本质上讲，该方法在一定程度上也可以看成是缩短了多个测向站之间距离的多站测向交叉无源定位的极限形式，不过所有测向站均位于同一个侦察站的站址范围内，所以从宏观应用上讲这也是一种单站定位应用形式。下面就分别从光波与微波频段的定位应用来进行分析。

3.1 光波频段的应用

早在20世纪第二次世界大战期间交战各方就普遍使用光学测距仪来对目标进行测向交叉的单站定位了。图1所示的是当时广泛使用的舰载光学测距仪，以此来引导火炮对海面或者空中目标实施准确射击。光学测距仪的基线有各种长度，例如：1m，1.5m，3m，5m等，二战时期日本的大和级战列舰大和号曾经装备过基线长15m的光学测距仪；网上公开展示的我国国产58式1m基线光学测距仪如图2所示，主要配发给单兵独立使用［9］。

图1 二战期间使用的典型舰载光学测距仪

图2 单兵使用的光学测距仪

不失一般性，在二维平面上来分析基于光学测距仪的单站无源定位原理。图1中的测距仪左右两端各有一个潜望镜A与B，两个潜望镜之间的距离固定且事先已知，记为基线长度dopb。两个潜望镜的光轴均能够绕着基线的垂线方向在很小的角度范围内转动，且转动角度θopA和θopB可实时精确测量。当人眼通过两个潜望镜合成的光路观察到同一个目标C时，就形成了如图3所示的平面几何关系［10］，为了表达清晰，图3仅示意性绘制。

图3 光学测距仪的测距与定位原理示意图

一般情况下由于目标距离远远大于光学测距仪的基线长度，即AC之间距离LAC≫dopb，BC之间的距离LBC≫dopb，并且θopA和θopB都非常小，几乎趋近于零。根据上述几何关系，在三角形ΔABC中由正弦定理可得：

由于θopA→0，θopB→0，所以由式（2）解得：

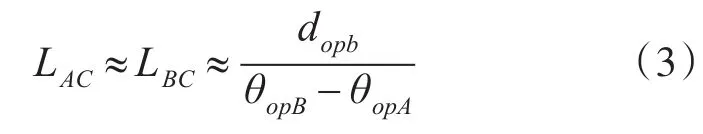
于是利用式（3）便可对目标与观察站之间的距离进行实时计算［11～12］。由于光学测距仪上的潜望镜绕其基线的垂线方向的转动角度很小，所以基于光学测距仪的单站定位需要将光学测距仪的基线中点M安装在一个转台上进行大角度范围转动来粗略对准目标，然后在此基础上，通过微调两个潜望镜的转动角度来精细对准目标。在图3中大角度转动的参考基线记为MO，大范围转动的角度是法线MF与参考基线MO之间的夹角∠FMO，记为θ∠FMO，并可被实时测量。如果以M为极坐标系的原点，MO为极坐标系的0°方向线，则被定位的目标C的极坐标(rob,θob)由下式表达：

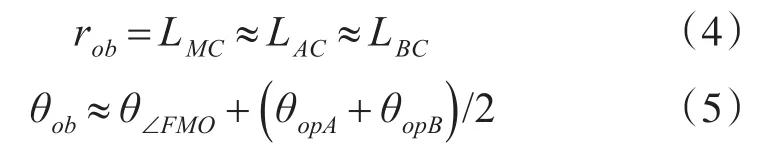
式（4）中LMC表示MC之间的距离。

除了基于光学测距仪的单站无源定位之外，使用同一艘舰艇上的激光无源侦察测向系统，通过两条测向线交叉也能够对反舰武器的激光照射源进行单站无源定位［13］，从而在实施舰载激光告警的同时，还能定位出反舰武器平台的位置，为舰艇自卫提供更多的防护信息。文献［14］还将这一定位体制应用于单站红外被动定位系统中，并研制了样机设备通过实验测试表明：此类单站红外被动定位方法不仅具有10%的定位精度，而且具有多目标定位能力。

3.2 微波频段的应用

图3所示的光学测距仪本质上是一个典型的两条测向线交叉的定位系统，目标C就是测向线AC与BC的交叉点，而C点的坐标位置也正是通过三角形ΔABC的几何关系而计算得到的，只不过这是一个非常奇异的被压扁拉长的三角形，两个长边AC与BC远远大于底边AB，即相当于超近距离的两点测向交叉定位。将这一单站定位体制从光波频段演进至微波频段，则有如图4所示的定位模型。

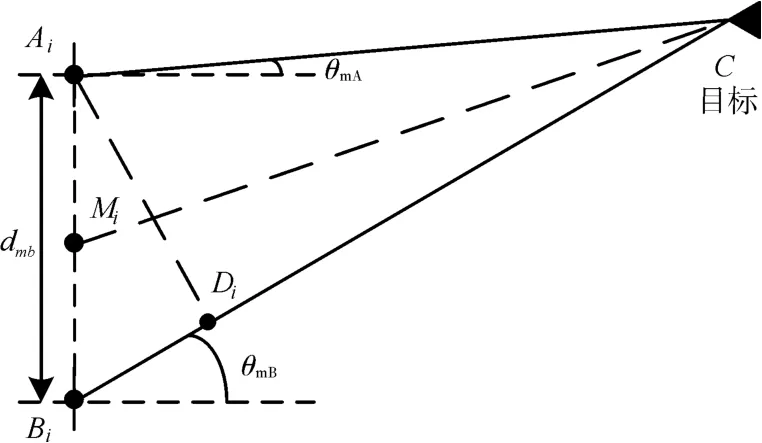
图4 微波频段的超近距离的双干涉仪测向交叉定位

由于微波频段的侦察接收天线通常具有较宽的接收波束，能够在较大的角度范围内直接接收目标辐射的电磁信号，所以将光波频段的潜望镜替换成具有测向功能的干涉仪，于是微波频段的部署距离很近的两个干涉仪Ai和Bi对目标C进行测向如图4所示，这与文献［15］中长基线对干涉仪无源测距思想是类似的。记图4中干涉仪Ai和Bi之间的距离为dmb，中点为Mi，且干涉仪基线位于同一条直线上，二者测量得到目标C的来波方向角度与干涉仪基线的法线之间的夹角分别为θmA和θmB。同样在图4所示应用场景中目标距离远远大于干涉仪Ai和Bi之间的距离，即AiC之间距离LAiC≫dmb，BiC之间的距离LBiC≫dmb，但是夹角θmA和θmB的取值范围较大，例如在[ ]-π/4,π/4 范围，所以虽然同样可由正弦定理列出类似于式（2）的关系式如下，但却不能得到类似于式（3）的近似过程。

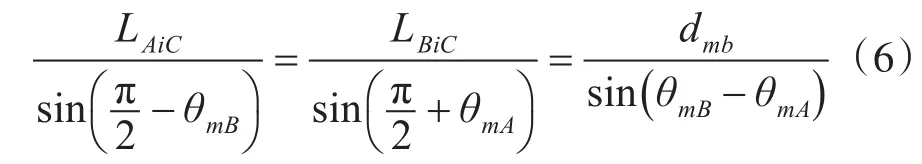
为求解该问题，在图4中过Ai点向直线段BiC做垂线，垂足为Di，由平面几何关系可得直角三角形ΔAiDiC中的两个锐角∠DiAiC和∠AiCDi，分别记为θ∠DiAiC和θ∠AiCDi，由下式所表达：

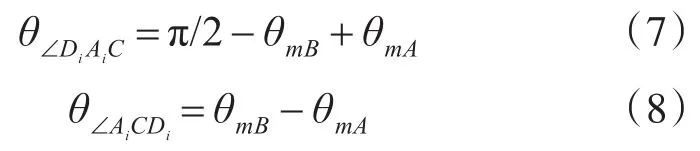
由于在直角三角形ΔAiDiC中LAiC≫LAiDi，所以θ∠AiCDi→0，于是可得：

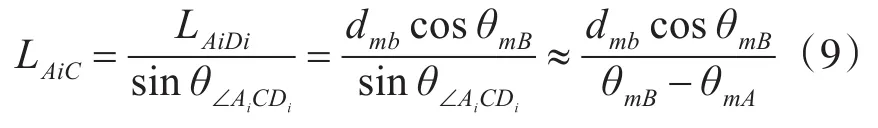
对比式（10）与式（3）可知，由于微波频段的两条测向线交叉的单站定位没有光学测距仪的整体旋转，所以在大角度范围内瞄准目标时，式（10）中分子所示的测距基线长度是随不同的测向角变化的。除此之外，二者的测距原理都是基于超近距离的两点测向交叉来实现的。如果同样以基线中点Mi为极坐标系的原点，MiBi为极坐标系的0°方向线，则目标C所在位置的极坐标(rib,θib)如下：

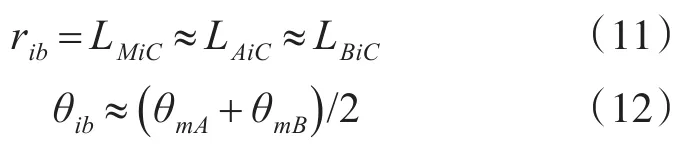
对比式（11）、式（12）与式（4）、式（5）可知，微波频段的超近距离两点测向后进行交叉的定位与基于光学测距仪的固定单站定位在数学模型上二者的测距功能是完全一样的。由于两点之间的距离dmb特别小，全部定位设备都能部署在同一个侦察站的站址范围内，所以在实际应用中也就将其简称为固定单站无源定位了。不过，不同文献对上述模型有不同角度的解释，例如文献［16］通过比相测距与测角来实现单站定位；文献［17］提出基于正交基线的球面波测量模型下的相位差解模糊方法来实现单站单脉冲定位；文献［18］提出基于等长基线相位干涉仪的单脉冲定位方法，利用等长基线干涉仪接收到辐射源信号球面波的波前相位2π模糊数相同的原理，通过等长基线相位差的差值和来波方向，确定辐射源与观测站之间的距离；而文献［19］通过设置多组相邻等长的干涉仪测向基线，模拟运动观测平台模型，并且将站间基线的长度缩短至百米量级，从而实现固定单站无源定位。实际上这些方法只是前述定位模型在形式上的变换，都可归入固定单站测向交叉定位这一大类之中，从本质上讲原理都是一样的。

4 定位精度与高精度测向的关系

由式（1）可知，在第一种测向线与约束面交叉的固定单站无源定位中测向精度越高定位误差越小。从定位解算的角度看，第二种多条测向线相互交叉的固定单站无源定位实际上由测角与测距两部分组成，首先对定位模型中的相对测距精度与作用范围分析如下。

1）相对测距精度

将图4中两个干涉仪的测向线所形成的夹角∠AiCBi记为θD，由几何关系可得：

在两个干涉仪之间的距离dmb固定，且测向角度θmA和θmB已测量得到的情况下，对固定单站测距式（10）等号两端求微分可得：

记测距相对误差为γL，单个干涉仪测角的绝对误差为θΔi，由式（10）和式（14）可得：

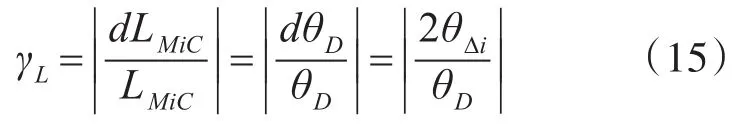
由式（15）可见，单个干涉仪的测角误差θΔi越小，单站测距的相对误差也越小，测距精度越高。

2）作用范围

对于多条测向线相互交叉的固定单站无源定位来讲，其作用范围主要由最大测距距离来描述。在实际应用所能接受的最大测距相对误差γL,max确定的情况，由式（10）与式（15）可计算得到最大测距距离LMiC,max如下：

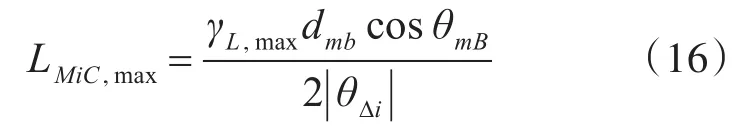
由此可知：在给定测距精度指标要求之后，固定单站的最大测距范围主要取决于单个干涉仪的测角误差θΔi，|θΔi|越小，单站测距的作用范围也越大。由于式（16）中含有cosθmB因子，所以被定位的目标位于干涉仪法向方向上的测距距离最大，随着目标方向偏离干涉仪法向，最大测距距离也会随偏离角度的余弦而减小。

综上所述，无论是基于光学测距仪的单站定位，还是微波频段的固定单站测向交叉定位，其中的关键点都是超高精度的测向。在光学测距仪中两个潜望镜转动角度的精确测量由精密机械结构来保证，而微波频段的固定单站定位通常采用相位干涉仪来完成高精度测向，其测向计算公式如下：

式（17）中φ为干涉仪两个通道之间的相位差测量值，θi为来波方向线与干涉仪基线法向之间的夹角。在干涉仪基线长度di和被测目标信号波长λ保持一定的情况下，通过对式（17）进行微分运算，可得干涉仪测向误差θΔi与通道间相位差测量误差φΔ之间的关系如下式所表达：

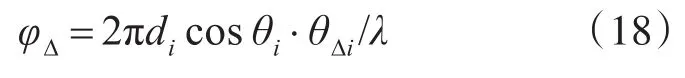
由式（18）可知，干涉仪高精度测向的关键环节在于尽可能地降低干涉仪通道间相位差测量误差φΔ，关于这一点在各类文献中有大量分析，不再重复展开阐述。在此根据前述理论分析结果，以图4所示原理给出一个应用示例进行具体说明。

本例中固定单站定位所使用的两个干涉仪中-π/4,π/4 ，测角误差θΔi=0.001°≈1.745×10-5rad ，即在干涉仪基线法向的±45°范围内均能实现信号来波方向测量，需要达到的相对测距精度γL=5%，被定位的辐射源目标的工作频率为10GHz，对应的信号波长λ=0.03m。由式（16）可计算出在干涉仪法向方向能够达到的最大测距距离LMiC,max=215km。由式（15）可计算出在最大作用距离上两个干涉仪的测向线之间的夹角θD=0.04°≈6.981×10-4rad。由式（18）可计算出在法向方向上干涉仪通道间信号的相位差测量误差φΔ=0.0731rad≈4.2°。在工程上通过各种误差校正算法与数据处理手段，以及多次测量累积等方式，完全能够实现干涉仪通道间信号的相位差测量误差控制在这一精度范围内［20］。所以采用长基线干涉仪高精度测向技术，此类固定单站测向交叉无源定位在工程上完全能够达到实用状态。点之间距离dmb=150m，每个干涉仪的测向基线长度di=20m，测角范围为[ ]

5 固定单站测向交叉无源定位的发展趋势

前面从定位模型、解算条件、典型示例等方面阐述了各种固定单站测向交叉无源定位方法从光波到微波的应用演进过程，这一定位体制在光波频段已经获得了极其广泛的应用，而在微波频段的应用中后续还需在如下几方面继续发展。

1）高精度微波干涉仪测向的工程实现

光波频段的固定单站测向交叉定位设备通常工作于可见光与近红外波段，波长范围大约在380nm～3000nm之间，这使得光学望远镜的测向精度非常高，测角误差很容易控制在1角秒以下。而微波频段的信号波长在10mm～1000mm的范围，与光波长相比有4个～6个数量级的差异，这就使得要实现微波频段的高精度测向工程难度较大。当前在微波频段一般都采用长基线干涉仪来完成高精度测向功能，按照前一节的分析，如进一步提升定位精度，甚至需要采用超长基线干涉仪，但为了在一个侦察站范围内实现全套设备的部署和单站操作，并考虑到各种工程因素，微波频段干涉仪基线最长也就在一两百米的量级。为了适应不同的作用距离，采用分布式连续超长基线干涉测量是较好的方法，在此类设计中自适应选取同一条直线段上的不同天线单元，根据任务来构建不同基线长度的干涉仪，通过灵活的相位差处理对不同距离上的电磁目标进行高精度测向与相位差解模糊计算。另一方面，影响干涉仪测向精度的工程因素较多，除了采用高效的误差标校、增强各个通道的一致性之外，通过各种信号处理方法来提升通道间信号的相位差测量精度，这都是提升测向精度的重要途径，虽然在此方面的理论研究工作已经开展得比较充分，但在工程设备的研制方面还需要进一步完善精细化的工艺流程，采取各种有效的技术手段来逼近理论极限。

2）在具备可观察性条件下，附加利用运动目标辐射信号中所包含的信息，综合提升定位精度。

如前所述，固定单站测向交叉无源定位不需要预先强制附加目标的任何运动约束条件，这是该方法的一大优点。但在实际应用中，如果面对的被定位电磁目标的确处于运动状态，并且也满足一定的观测条件，例如：该目标有较大的切向运动速度，运动状态比较稳定，几乎没有机动。在如此情况下，进一步从电磁目标所辐射的信号中挖掘信息，即通过截获的电磁目标信号对目标的运动速度分量进行直接测量或间接推算，采用各种跟踪滤波手段进行连续的平滑滤波，则能够从目标的运动模型中提取出与距离相关的信息，关于这一点在目前的固定单站对运动目标的无源定位技术方向上发表了大量的文献，报道了各种推算方法［21～22］，在此不再展开阐述。但需要指出的是，将上述这些方法结合起来应用，则能够获得更加精确的固定单站无源定位结果。在目标运动状态的可观测性降低时，例如：对着侦察站径向运动、连续地大型机动等，此时就要充分发挥固定单站测向交叉无源定位的作用；而在可观测性较好时，例如沿切向做匀速直线运动，此时就要充分利用目标的运动状态信息，借助电子侦察中辐射源信号参数的高精度测量手段，实现目标运动状态的精确估计与跟踪，并将测量结果作为附加信息，增加定位方程进行联合求解，则可达到进一步提升固定单站无源定位精度的目的。

6 结语

固定单站测向交叉无源定位主要分为两种：单条测向线与目标所在约束面交叉的无源定位；多条测向线相互交叉的无源定位。本文从定位模型、解算条件、典型示例等角度对上述方法从光波到微波的应用演进过程和交融关联关系进行了综合性分析，揭示了高精度测向在其中所发挥的核心关键作用，并对其未来发展趋势进行了展望。这有助于更加深刻地理解与认识固定单站测向交叉无源定位的本质，进一步推进工程应用实践，从而为固定单站无源定位的应用研究提供了另一个视角的参考。