航母编队航渡中舰载预警机兵力行动分析∗

孙秀文 吴 刚 唐 晨

（海军指挥学院 南京 210016）

1 引言

航母编队具有综合作战能力强、遂行任务多样、威慑力大等优势，但由于机动能力弱、目标庞大，也极易受到来自空中的打击，因此防空作战至关重要，是航母编队的主要作战样式之一［1～2］。

航母编队航渡中对空防御通常建立起远、中、近三层防御体系，其中远程拦截区距离航母约180km～400km（舰载预警直升机配置为200km，固定翼预警机为400km），由于我国航母暂不具备搭载固定翼预警机的能力，因此远程对空警戒兵力主要由舰载预警直升机、掩护歼击机、哨舰等兵力组成［3～4］。当实施远程对空警戒时，通常以航母与主要威胁方向（如敌机场、敌航母编队方向等）的连线为威胁轴，预警直升机在该威胁轴方位上前出至一定距离垂直于威胁轴往返机动实施警戒，歼击机、哨舰在其附近实施掩护［5］。

在无明显敌情征候的情况下，通常选取航母编队的正前方或侧前方作为威胁轴方向，预警直升机在该方位与航母保持相对阵位不变实施警戒［6］；但当有明显敌情征候时，如经过固定的敌机场，那么航母与敌机场连线所形成的威胁轴将随着航母的航行而随之变化，同时舰载预警直升机的配置和行动也要随之改变。在现有有关航母编队预警机配置的研究中，多是基于第一种情况进行的建模分析，如文献［7～9］中，作者基于某一威胁轴方位不变，从预警机前出配置需考虑的因素着手，分析了预警机前出距离、巡逻空域和行动方法；文献［10］通过分析对空防御作战过程，提出了前出距离的确定方法；文献［11］对预警直升机阵位配置后的警戒能力进行了数理分析，给出了影响其警戒能力的因素。这些研究成果虽对航母编队舰载预警直升机的优化配置起到了借鉴作用，但都没有考虑威胁轴随航母编队运动而改变的情况，而这恰是实际作战中经常遇到的场景，因此研究航渡中警戒直升机随威胁轴变化的机动方法，对航母防空作战至关重要。

2 问题重塑

假设航母位于某海域向北航行，路经敌某一机场，根据文献［5］那么航母与敌机场的连线即为威胁轴方向，为及早获取敌空中目标信息，航母舰载预警直升机应始终配置在该方位一定距离上。由于威胁轴方位不断随航母运动而偏转，因而舰载预警机也将随之偏转，总体看舰载预警机的飞行轨迹将一边随着航母编队向北运动，一边向左发生偏转（以便始终垂直与威胁轴往返机动）。为便于舰载预警机与航母协同行动，确保舰载预警机始终垂直于敌机来袭方向对空警戒，需要给出直升机每次往返飞行的时间、偏转航向。

3 模型构建

如图1所示，假设t0时航母位于H0点，向北航渡，航速为V航母，敌机场（基地）位于左正横O点，舰载预警机位于威胁轴上的Z0点，距离O点距离为d1，距离H0点为d2，南北往返运动时，航速为V直升机，向北或向南的巡逻线长度为d3。t1时刻，航母航渡至H1位置，此时舰载预警机位于Z1点，现分析预警直升机沿或飞行的时间和飞行的航向。

以O点为中心，建立直角坐标系，OH0为X轴的正方向，H0H1为Y轴的正方向，则t0时航母位置点坐标为H0（d1+d2，0）；舰载预警机的位置点坐标为Z0（d1，0），巡逻线北端点Z0上坐标为（d1，d3），南端点Z0下坐标为（d1，-d3）。由于航渡过程中，舰载预警机巡逻线中心点要始终保持在威胁轴方位、距离航母d2的距离上，因此在航母不断向北运动过程中，等效于舰载预警机巡逻线的中心点在围绕航母为圆心，d2为半径逆时针做圆周运动，且巡逻线相切于圆周。设t1时刻航母相对于原位置产生的偏转角为γ，即∠H0OH1=γ，容易证明γ；过Z1点作Z0′H1的垂线，交 Z0′H1于Z1′点，根据直角△Z1′Z1H1性质可得，任意时刻巡逻线中心位置点坐标为

图1 舰载预警直升机巡逻线中心点运动轨迹图

过 Z1上作 Z1′Z1的垂线交 Z1′Z1于 Z1上′，容易证明∠Z1上Z1Z1上′=γ，根据直角△Z1上Z1Z1上′性质可得，任意时刻巡逻线北端点坐标为

同理根据直角△Z1下Z1Z1下′性质可得，任意时刻巡逻线南端点坐标为

任意时刻舰载预警机向北飞行时的坐标为

其中ti表示第i次向北单次巡逻飞行的时间，Zix、Ziy表示ti时刻舰载预警机的横、纵坐标。

同理，任意时刻舰载预警机向南飞行时的坐标为

航渡中巡逻线中心点以及南北端点的运动轨迹如图2所示。

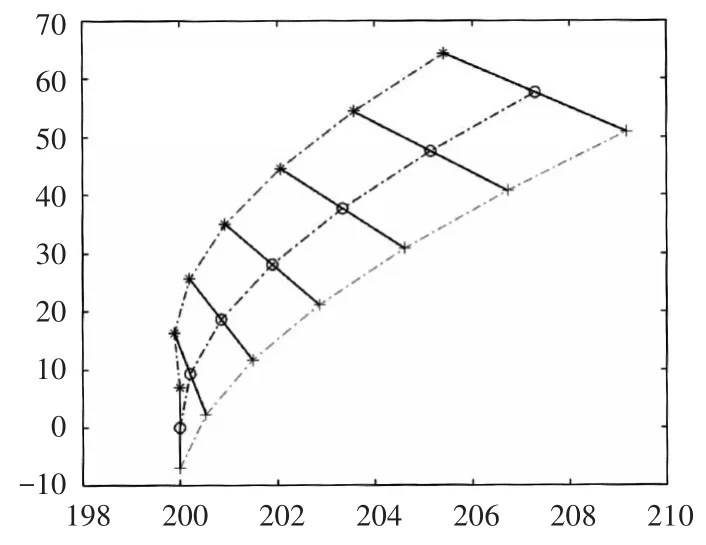
图2 舰载预警直升机巡逻路径变化图

图中“*”表示巡逻线北端点的运动轨迹，“○”表示中心点的运动轨迹，“+”表示南端点的运动轨迹。从图中可以看到在舰载预警机沿着南北端点往返运动时，由于威胁轴方位在时刻变化，故巡逻线也在时刻发生变化和偏转，理想情况是舰载预警机在往返运动时一边运动一边进行偏转，任意时刻都在理想的南北端点连线上巡逻，但事实上这样很难操作。简便可行的方法是直升机一定时间内沿着图中某条巡逻线航行，待与北（南）端点接近到最小距离时，返回修正至下一航线。

由式（1）～（5）可得，舰载预警机沿着某个航向向北航行时，其位置点Zi距北端点Zi上距离为

舰载预警机沿着某个航向向南航行时，其位置点 Zi距南端点 Zi下距离为

4 仿真分析

为验证分析上述公式的可行性，根据现行装备的战技性能，设基础数据如表1［12］。

表1 仿真参数表

利用Matlab进行仿真计算，范围0≤γ≤45°，步长1s，可得舰载预警机的机动轨迹如图3（a）所示，图中“○”表示舰载预警机的转向点；“+”表示南北端点；蓝色“-”表示向北巡逻，红色“-”表示向南巡逻，黑色“-”表示直升机转向修正，相关数据如表2。

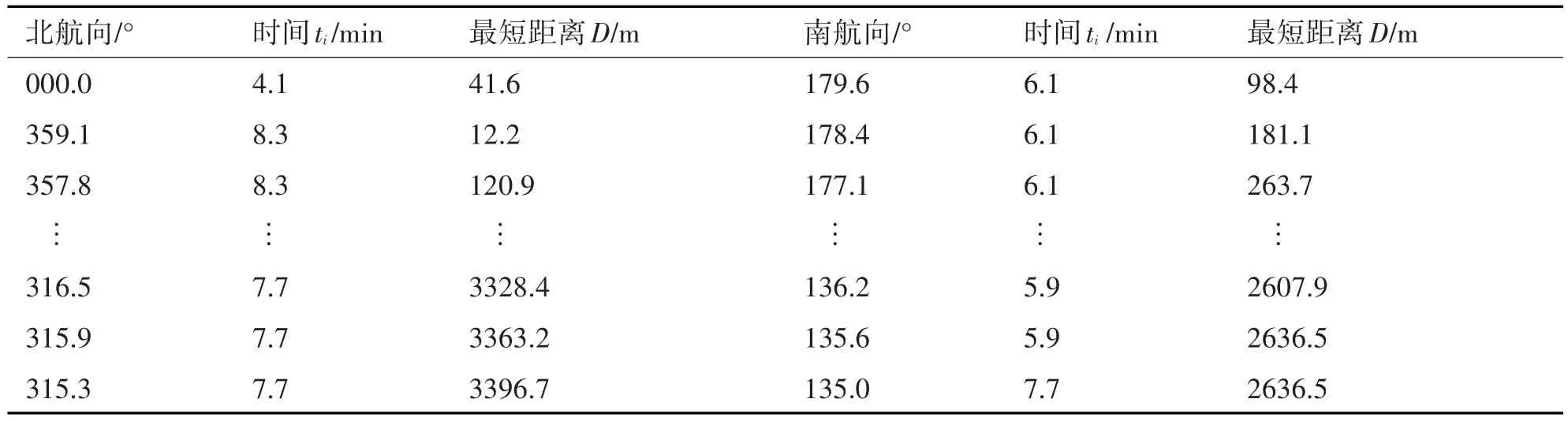
表2 修正前直升机飞行轨迹参数表

由表2结合图3（a）可以看到，随着γ的增大，舰载预警机转向时与南北端点的最短距离不断增大，即误差不断增大，为抵消误差，当舰载预警机向南北运动时需要修正一个角度，且修正角的大小要随着γ的增大不断增大，下面进一步分析修正角大小的问题。

由于舰载预警机转向时与南北端点是最短距离，因此舰载预警机转向点与巡逻线端点的连线近似垂直于舰载预警机的飞行轨迹（巡逻线），因此修正角：

图3 舰载预警机修正前后飞行轨迹图

表3 修正后直升机飞行轨迹参数表

由图3（b）和表3可以看出，修正之后的偏差距离得到了明显改善，误差基本控制在50m误差范围之内，有利于舰载预警机的精确规划飞行。

5 结语

论文以航母编队航渡中舰载预警机警戒巡逻机动方式为问题，采用建模仿真的方法，探索了航母向北航行时偏转角在0～45°范围内的直升机飞行轨迹和相关飞行参数，为航渡中航母编队舰载预警机的飞行提供了一定参考依据。下步，可以以此为基础，继续探究航母编队在不同航向、不同速度时的飞行轨迹和参数，以设计出适应航母任意航向和速度航行时，舰载预警机的飞行参数。