基于弹性网的两阶段模型平均方法及应用研究*

魏 巍,王星惠,陈晓星

(安徽大学)

0 引言

在大数据时代背景下，随着计算机收集、储存数据的技术不断发展，数据规模越来越大，数据维度也越来越高.经研究发现这类高维数据中只有极少数被认为与预测真正相关，如何从繁杂的数据中寻找出有效的信息也成为国内外研究的热点.

针对维数祸根问题，目前流行的高维变量选择方法是由Tibsniran提出的Lasso方法，该方法在一般线性最小二乘的前提下通过惩罚将无影响和弱影响的变量的参数压缩为零，以实现降维功能[1].刘睿智和杜溦将基于变量选择观点的Lasso选择方法运用到资产选择和预测中，取得了很好的效果[3].Wu等在指数追踪时使用Lasso方法，并在实证分析中取得较好效果[4].在Lasso方法的基础上，Zou提出的自适应 Lasso方法，不仅克服了Lasso方法对重要变量的系数估计有偏且不具有 Oracle 性质的问题，而且还具备良好的实用性[5].秦晔玲和朱建平利用自适应Lasso方法对深沪300指数的指数追踪进行分析，研究发现该方法在股票选择和有很好的效果[6].但高维数据通常存在多重共线性问题，Lasso方法处理这类数据效果不佳，为克服这一问题， Zou 和Hastie提出了一种改进的Lasso算法——弹性网方法，可以克服原始数据中的共线性与群组效应，能有效地处理高维数据[7].Wu和Yang将弹性网方法运用到沪深300指数和上证180指数跟踪上，研究表明弹性网方法比Lasso方法具有更好的表现[8].

模型选择(Model Selection, MS)因其简单性和可解释性在统计建模中一直占据重要地位[9-14].但模型选择过程或多或少存在一些缺陷[15-16]，会带来不确定性，可能使估计或预测的误差偏大，导致模型预测效果变差.为了弥补这些缺陷，越来越多的学者开始关注模型平均方法(Model Averaging, MA).模型平均通过给一组相互竞争的候选模型赋权，获得一个加权平均的预测值.该预测值充分利用了各候选模型的信息，因而具有更高的模型预测精度，模型更加稳健.模型平均方法主要有两个发展方向：Bayes模型平均方法(BMA)和频率模型平均方法(FMA).该文考虑的是频率模型平均方法[17]，它的最优权重选取是至关重要的，当下常见的权重选择方法包括Smoothed AIC(S-AIC)、Smoothed BIC(S-BIC)方法[18]、基于Mallows准则的MMA(Mallows Model Averaging)[19]和基于Jackknife准则的JMA(Jackknife Model Averaging)[20]等.

Hu等研究发现，在大多数情况下，模型平均比单个模型的预测精度高，但是在单个模型中存在许多变量时，模型平均与模型选择相比没有什么改善[21].针对这种情况，Ando和Li提出了一种应用于高维数据的两步交叉验证方法(MCV)，先通过预测变量与响应变量间的边际相关性构建候选模型，再通过Jackknife准则来估计模型权重，这是高维频率模型平均发展的重要一步[22].根据类似的思想，Ando和Li进一步将模型平均扩展到高维广义线性模型[23].Pan在Ando和Li研究的基础上加以思考，提出了一个改进的两阶段模型平均方法(IMA)，先通过高维变量选择方法筛选变量并构建候选模型，再运用Jackknife准则来优化模型权重进行模型平均，最后将该方法应用于叶黄素数据中[24].研究发现与MCV相比，IMA具有更优秀的预测性能，更适合高维数据.

受上述文献的启发，该文试图将弹性网与Jackknife模型平均方法相结合，提出了一种基于弹性网的两阶段模型平均方法(弹性网-JMA)，以上证180指数及其所有成分股的30分钟线收盘价为研究对象.通过基于弹性网的变量选择方法对上证180指数的所有成分股进行具体的股票选择以实现降维的目标，并构建稀疏的候选模型，再通过Jackknife模型平均方法对上证180指数的30分钟线收盘价进行预测.为了比较弹性网-JMA的预测效果，该文考虑了多种基准模型用于对比分析，分别是Lasso回归、弹性网回归、基于Lasso的两阶段模型平均方法(Lasso-MMA 和Lasso-JMA)以及基于弹性网的两阶段Mallows模型平均方法(弹性网-MMA).实验结果表明：该文提出的弹性网-JMA的预测性能优于其他基准模型，实证结果表明该方法的优越性.

1 理论模型

1.1 模型建立

(1)

其中，yt是第t次观测的被解释变量，xt=(xt1,xt2,…,xtp)T是第t次观测的全部解释变量，xtj是第t次观测的第j个解释变量，βj是第j个解释变量的回归系数，独立随机误差εt是零均值且有限方差σ2.该文研究过程中，假设只有一部分解释变量在预测被解释变量是有贡献，表示真实解释变量(即具有非零回归系数的解释变量)的数量为s，s和真实解释变量是未知的.

为了后续书写方便，将模型(1)表示为矩阵形式：

y=Xβ+ε

(2)

其中，

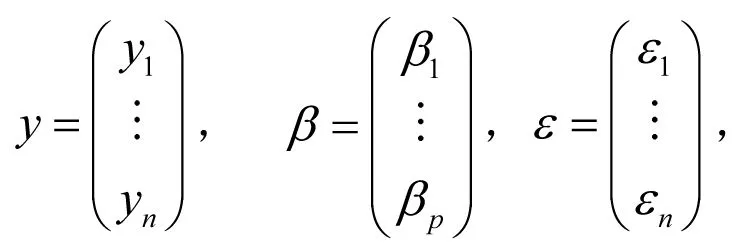
1.2 模型原理与研究框架

1.2.1 Lasso方法

Tibshirani提出Lasso方法[1].不失一般性，假定对被解释变量y进行中心化，对解释变量X进行标准化，即

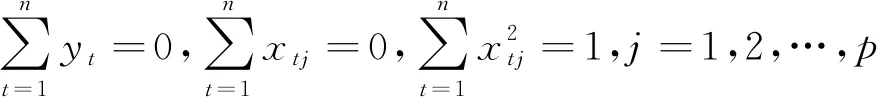
(3)

Lasso估计定义为：

(4)

Lasso方法是在最小二乘的基础上加入约束，使得非零回归系数βj向0收缩，选择出更具有价值的解释变量.Lasso方法能降低预测方差，实现变量选择，但是也存在一定的局限性.对于n×p的解释变量，最多只能选出min(n,p)个变量.当p≫n时，最多只能选择n个解释变量，会影响到模型的预测精度，对建模带来误导.

1.2.2 弹性网

针对Lasso回归的局限性，Zou 和Hastie在Lasso回归方法的基础上提出了弹性网回归方法[7].弹性网估计定义为：

(5)

(6)

1.2.3 模型平均方法

模型平均方法是把候选模型通过一定的权重进行加权平均形成一个新的组合预测模型，各个候选模型权重的确定尤为重要，确定模型平均权重的准则诸多，该文考虑MMA和JMA方法.

MMA方法是由Hansen提出的一种常数权重模型平均方法，他首次将Mallows准则引入到模型平均方法当中，通过极小化Mallows准则来得到各个候选模型的权重[19].

(7)

权重选择的Mallows准则是：

(8)

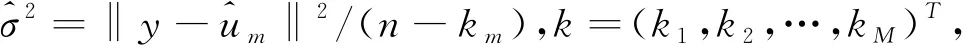
(9)

综上所述，可得到MMA方法估计值为：

(10)

第t*个被解释变量yt*的预测表达式为：

(11)

Hansen 和 Racine提出了JMA方法，它是常数权重模型平均方法中比较有代表性的一个方法.JMA方法适用于随机误差为同方差和异方差的情形，弥补了MMA方法只能用于同方差的不足，适用性更优[20].

(12)

则条件均值u的Jackknife模型平均估计值为：

(13)

接下来，基于Jackknife准则来选择权重向量.Jackknife准则为：

(14)

通过极小化Jackknife准则得到权重向量：

(15)

综上所述，可得到Jackknife模型平均估计值为：

(16)

第t*个被解释变量yt*的预测表达式为：

(17)

1.2.4 两阶段模型平均方法

该文提出基于弹性网的两阶段模型平均方法，具体步骤如下.

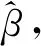
第二步：模型平均.通过极小化Jackknife准则来估计各个候选模型的权重，再在测试集T2上，对各个稀疏的候选模型进行赋权获得被解释变量yt*的预测值.具体的过程如1.2.3所述.

2 实证研究

2.1 数据描述

考虑数据的可得性以及上证180指数的成分股每半年更新一次的事实，该文选取2021年6月12日至2021年12月10日的上证180指数及其所有成分股的30分钟线收盘价为研究对象，对由于股票停牌无法交易而导致的缺失值，用该股票停牌前一日的收盘价填充.该文研究的数据集共976条观测值，180个指标.按照时间顺序，将数据集按7∶3的比例分为训练集和测试集，用训练集来估计变量筛选后的候选模型的权重，用测试集来评估各模型的预测表现.

2.2 模型与分析

该文考虑一个多元线性模型，表示如下：

(18)

研究过程中，令yt表示上证180指数的第t次观测值，xtj表示第j只上证成分股30分钟线收盘价的第t次观测值.

为了让股指追踪的成本更低，期望可以通过成分股中一个较小的子集就能追踪指数的表现.为实现这一目的，考虑对上证180指数的180个成分股进行变量筛选，在惩罚回归中，通过程序自动选择使交叉验证预测误差最小的调整参数，由此选出合适的成分股子集，在训练集上构建候选模型，再估计候选模型的权重，在测试集上运用加权后的模型计算R2，均方根误差(RMSE)和平均绝对百分误差(MAPE)，以此作为模型的评价指标，R2越大，RMSE和MAPE越小，表示预测精度越高，三者的定义如下：

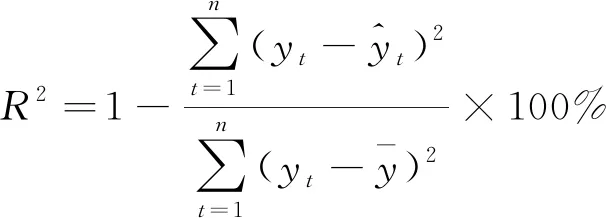
(19)

(20)

(21)

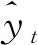
在该节中，为了评估两阶段模型平均方法进行上证180指数30分钟收盘价预测的表现，选择了6个预测模型进行对比，分别是Lasso回归、弹性网回归、Lasso-MMA、Lasso-JMA、弹性网-MMA和弹性网-JMA方法.Lasso回归和弹性网回归都是直接用全部成分股的30分钟线收盘价来预测，旨在与两阶段模型平均方法进行对比.两阶段模型平均方法使用不同的降维方法，旨在探究用不同的惩罚函数进行变量筛选是否会显著影响模型的预测表现；使用不同的权重选择方法，旨在探究基于不同的渐近最优的模型平均方法是否会显著影响模型的预测表现.

2.3 实证结果分析

图1展示了各模型预测上证180指数30分钟线收盘价的情况，可直观地显示了各模型在各期地预测表现.

从图1中可以发现：相比与两阶段模型平均方法，Lasso回归和弹性网回归的预测波动较大，预测模型不稳定，尤其是Lasso回归，而四种两阶段模型平均方法的预测结果较为一致，折线图基本重合，更贴近实际值.

图1 各模型的预测表现

接下来，将从R2、均方根误差(RMSE)和平均绝对百分误差(MAPE)三个方面来定量分析各模型的整体预测效果，具体数值见表1.由于各模型在不同的评价指标下有不同的预测表现，该文提供了一个综合排名来评价预测表现.要确定综合排名，首先要分别在同一指标下对各模型进行排名，再对同一模型的不同指标进行简单平均，综合排名越靠前则模型预测性能越好.

表1 各模型的整体预测表现的对比

(1)从综合排名来看，两阶段模型平均的预测效果一致优于Lasso回归和弹性网回归，两阶段模型平均方法的预测精度有了明显的提高.在四种两阶段模型平均中，基于弹性网降维的两阶段模型平均一致优于基于Lasso降维的两阶段模型平均，说明使用组合惩罚函数进行变量筛选会显著提高模型的预测精度；使用JMA方法的两阶段方法的预测表现也优于MMA方法，说明基于不同的渐近最优的模型平均方法也会显著影响模型的预测精度.

(2)在R2评价准则下，Lasso-JMA表现最优，弹性网-JMA表现次之，但两者的指标差值低于0.05，说明就该指标来看，两者预测性能相当.

(3)在RMSE和MAPE两种评价准则下，弹性网-JMA表现最优，其次是弹性网-MMA，说明弹性网降维在预测中优势明显，这一发现是令人振奋的，因为弹性网降维会使更多的非零回归系数向0收缩以获得更低维度的解释变量，实现降低股指追踪的成本的同时提高了预测精度.

3 研究结论

准确的上证180指数的预测为股指追踪提供便利.该文运用两阶段模型平均方法预测上证180指数30分钟线收盘价，利用部分成分股来估计目标指数，降低股指追踪的成本.研究结果显示，弹性网-JMA方法在预测上证180指数30分钟收盘价时表现出了突出、稳定的预测性能.两阶段模型平均方法优于Lasso回归和弹性网回归，而弹性网-JMA方法又优于另外三种两阶段模型平均方法.这说明弹性网-JMA方法可以有效降低预测误差，是一种有效的股指预测模型.

该文在研究两阶段模型平均方法时发现，不同的降维手段对模型预测性能有很大的影响，关于两阶段模型平均方法中降维部分还可继续进行深入研究.