基于OCSVM的压力钢管健康监测数据的异常检测

尚 鑫，方超群，武东辉

（1.国网新源控股有限公司北京十三陵蓄能电厂，北京市 102200；2.水利部水工金属结构质量检验测试中心，河南省郑州市 450044；3.郑州轻工业大学，河南省郑州市 450001）

0 引言

北京十三陵抽水蓄能电站位于北京市昌平区蟒山，是我国北方地区建成的第一座大型抽水蓄能电站。该电站利用已经建成的十三陵水库为下库，左岸蟒山的上寺沟为上库，由引水系统和尾水系统连接上库和下库。发电厂房位于蟒山岩体内，电站装机容量为4×200MW，采用“一管两机”布置方式，由两个相互独立的水道系统组成，包括上库进/出水口、引水事故闸门、引水隧洞、引水调压井、压力管道、尾水支管、尾水事故闸门室、尾水调压井、尾水隧洞、下库进/出水口等建筑物[1]。

本文的数据来源是布置在电站引水系统压力管道明管段处安装的在线监测系统所采集压力钢管主管、1号支管和2号支管明管段在设备运行时的应力、振动、温度、噪声、地震[2]等参数。通过对该在线监测系统45天的历史数据调取，实现本次数据分析所使用的基础数据集。再通过对数据集进行计算机人工智能分析，实现对设备健康状态的监测判断[3]。

1 数据集的选取

水电站引水压力钢管在运行过程中，其在线监测所产生的设备健康监测数据对设备的异常检测和安全评估具有现实意义[4]。通过对压力钢管进行健康监测，可获得压力钢管在运行过程中的振动、应力、温度、位移、地震等参数信息，这些信息经过数据保存，可形成完备的压力钢管安全运行历史数据，监测传感器安装区域如图1所示。

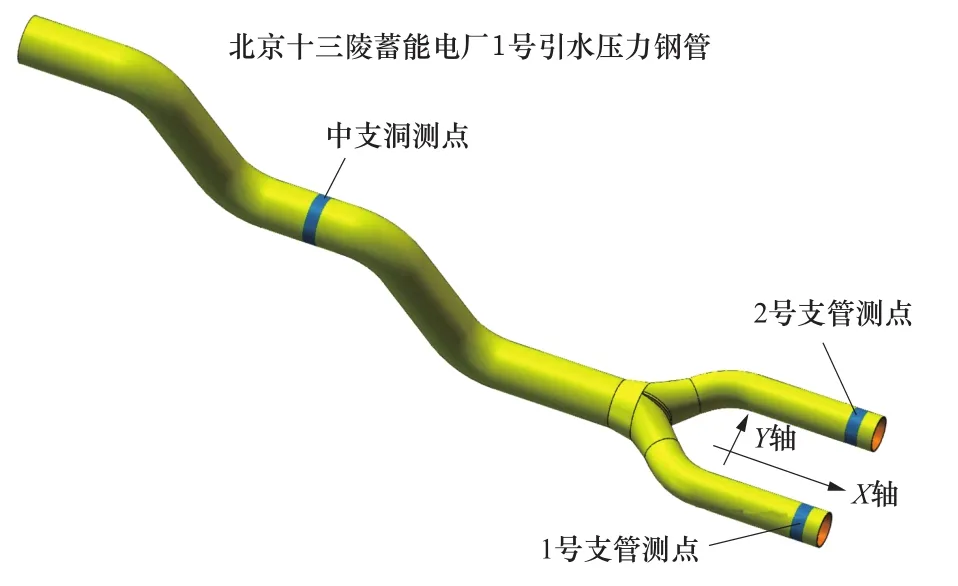
图1 1号压力钢管传感器监测区域示意图Figure 1 Schematic diagram of No.1 steel penstock sensor monitoring area

本次采用的数据为北京十三陵蓄能电站1号引水系统压力钢管的1号支管和2号支管在45天时间内所产生的历史数据，由于压力钢管健康状况监测所用的传感器较多，且每个传感器监测的数据较大，本文仅提取对设备安全运行相关性较大的振动、应力两个参数进行运算分析。运算使用的数据采样周期为5min，该采样周期既保证了设备运行的数据特征不被漏采，也最大可能地包含了压力钢管在机组发电、抽水以及停机状态下的参数信息[5]。

经过数据整理，采用4个监测点位的数据进行数据集的建立，每个监测点位均包含振动加速度监测参数和应力监测参数。4组通道的振动加速度原始变化曲线和应力原始值变化曲线如图2和图3所示。

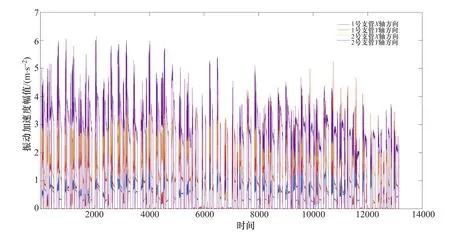
图2 4组通道振动加速度原始值变化曲线Figure 2 4 groups of channel vibration acceleration original value change curve

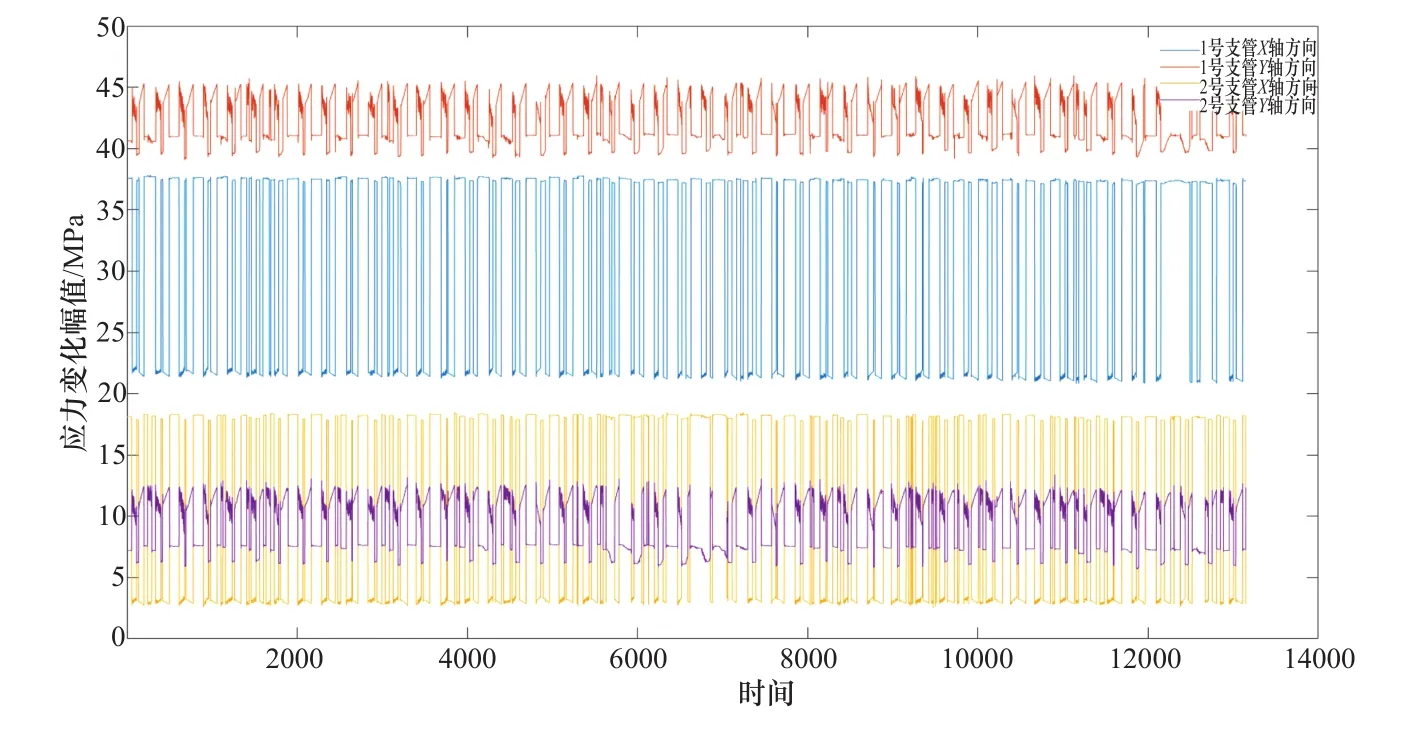
图3 4组通道应力原始值变化曲线Figure 3 4 groups of channel stress original value change curve

经过分析并经过数据整理，将每组数据集限定为13000个样本。4个监测点的数据集即可分为：1号支管X轴方向的“振动-应力”数据集、1号支管Y轴方向的“振动-应力”数据集、2号支管X轴方向的“振动-应力”数据集和2号支管Y轴方向的“振动-应力”数据集。

2 基于无监督学习的异常值检测

2.1 异常值检测

异常检测（anomaly detection）是对不匹配预期模式或数据集中其他项目的项目、事件或观测值的识别，异常也被称为离群值、噪声、偏差等[6-7]。异常检测是机器学习算法的一种，它通过大量的测试值以检测是否有异常值的存在，可应用于各个行业，例如设备故障的检测以及大型设备设施中的实时监测和发现。

算法是从数据集中学习数据特征，并为其设定“参考基准值”，当新进入的数据超过预定义为正常范围的阈值时，则将新数据与“参考基准值”偏离的程度作为概率输出。异常监测大致可分为监督学习、半监督学习和无监督学习3种方法。如果没有足够的历史数据或数据集中的数据没有标签，则使用“无监督学习”将是较为理想的方法。

2.2 样本特征

机器学习均属于分类算法，如果将分类算法进行划分，根据类别个数的不同可以分为单分类、二分类、多分类。常见的分类算法主要解决二分类和多分类问题，如图片分类、手写体识别、人脸识别等，这些算法并不能很好地应用在单分类上[8]。但是，在工业实时在线监测或工业应用方面，单分类问题占据了绝大多数。

工业应用中，很多样本无法找到负样本，即使有负样本，该样本个数也非常少，会造成训练集的不平衡。如果人为制造一些负样本或通过数据筛查整理出一些负样本，也会因为负样本的污染而无法达到预期的目标。所以，在只有正样本而没有负样本的场景中，使用单分类算法则会更加合适。本文采用的压力钢管健康检测数据均为正样本，该数据也为单样本数据集。

人工智能的大部分算法对数据集的要求相对较高，数据集的质量也是影响其算法准确率的保障，所以，一般用于训练的数据集均需要有标签[9]。但压力钢管健康状态的监测数据集没有标签，也不可能对在线的数据进行一一标注。对于没有标签且为单样本的数据集，只能采用单样本分类算法，而单样本分类算法只关注与样本的相似或者匹配程度，对于偏离的未知数据则不下结论。

2.3 算法选择

对于单样本数据的异常检测，目前常用的算法有单分类算法（one class learning）[10-11]、神经网络算法（artificial neural network）和孤立森林算法（isolation forest）[12]等。

单分类算法比较经典的是单类支持向量机（one class SVM，OCSVM），该算法是通过拟合一个超平面将样本中的正面特征分隔，并用该超平面为预测结果做出决策，在正面特征集中的样本系统就认为是正样本，不在正面特征集中的样本系统则认为是异常值。但该算法中一般采用高斯核，由于在核函数计算时相对比较耗时，所以在海量数据的场景下会耗费大量的计算资源。

异常检测还可以使用神经网络算法来实现，该算法在深度学习中被广泛使用，其自编码算法可以应用在单分类的问题上，自编码是一个BP神经网络，网络输入层和输出层一样，但中间层的层数比较灵活，可以为单层也可以为多层，若中间层的节点数比输出层少，则中间层就相当于对数据进行了抽象和压缩，借此实现无监督的方式来学习数据的特征。如果仅有正样本数据，就可以利用正样本训练出一个自编码器，而自编码器就是一个单分类的一个模型，当对全量数据进行预测时，通过比较输入层和输出层的相似程度就可以判断输入是否属于正样本。由于采用了神经网络，就可以用GPU来加速运算，因此该方法比较适合海量数据的场景。

孤立森林是一个相对高效的异常点检测算法。当进行检测时，系统会随机选取一个特征，并在特征的最大值和最小值之间选择一个分切面，然后再进行其他特征的分切，通过不断的“递归-划分”，最终就像一棵树，称为决策树。算法对数据划分的次数则等于根节点到叶子节点的路径距离。为增强鲁棒性，该系统会随机生成很多树并形成森林，在“森林”中只需要关注最容易被“孤立”出来的那些点，即可判断该点是否为异常值。孤立森林运算量小且算法特性也决定了它可以应用在分布式训练场景，所以适合海量数据。但如果训练数据为高维度数据，则该算法没有优势。

对于本文采用的小样本参数的设备健康数据集，采用单分类支持向量机算法有其相应的优势：

（1）可以解决小样本下机器学习的问题，这是神经网络算法和孤立森林算法所不及的。

（2）解决了非线性问题，该问题一直是机器学习中无法绕开的话题。

（3）无局部极小值问题，而采用神经网络算法则有可能陷入局部极小值。

（4）可以很好地处理高维度数据集。

（5）泛化能力比较强，而孤立森林采用决策树的算法则容易过拟合，导致泛化能力不强。

单分类支持向量机算法也有核函数在高维映射解释力不强、对缺失数据敏感的缺点，但本文在应用该算法过程中，已通过数据前期处理解决了缺失数据的问题。所以，本文将通过单类支持向量机的计算方法对设备的历史运行数据进行运算分析。

2.4 单类支持向量机（OCSVM）

单类支持向量机属于支持向量机的范畴，但其与基于监督学习的分类回归支持向量机不同，它是无监督学习，不需要对训练集进行标注。单类支持向量机采用支持向量域（support vector domain description）的解放思想，对于支持向量域，需将不是异常的样本均划归为正类别，该算法采用一个超球体对数据进行划分，在特征空间中计算数据周围的球形边界，并最小化这个超球体体积，同时也最小化了异常点对整个数据的影响。

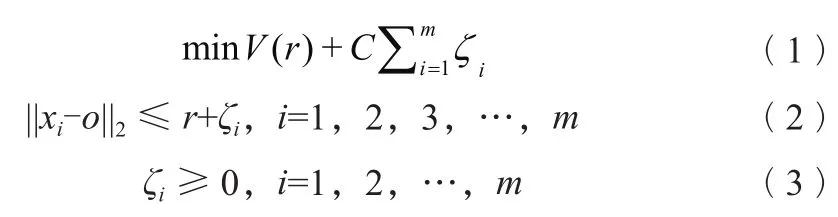
式中：o——超球体中心；

r——超球体半径；

V(r)——超球体体积；

C——惩罚系数；

ζi——松弛变量；

xi——训练点。

采用拉格朗日对偶求解之后，首先判断新计算的数据是否在内，如果新计算的数据点到球心的距离小于球体的半径，可判断该数据不是异常点，如果到球心的距离大于球体半径，即判断该数据为异常点。

因为数据本没有标签，所以算法不对数据进行分类判别，而是通过回答“是”或“不是”的方法根据支持向量域将样本数据训练出一个最小的大于三维特征的超球面，其中，在二维中则是一个曲线，曲线会将数据包起来，曲线之外的数据即为异常点。

3 算例分析

3.1 数据分析环境

本文采用Python+Numpy+Sklearn+Matplotlib的组合进行数据处理并绘图。首先通过Python连接数据库，并对数据库相对应的数据通道进行二次数据采集，采集的间隔为每5min一个采样点，并将采样点以多维矩阵的形式保存在Numpy数组中。由于数据库每条通道的原始数据时间戳不完全相同，所以在对数据库的读取过程中，增加了时间校验程序，当该通道的数据满足二次采样间隔并处于±6s的时间范围内时，该数据才为有效数据，否则按无效采样点处理。

3.2 数据预处理

完成数据二次采样后，需要对数据进行预处理。首先对数据进行清洗，剔除无效采样点。当剔除无效采样点后会出现数据空缺，对于数据空缺目前有多种处理方法，使用较多的有两种：一种是通过条件均值进行数据集的填补，另外一种是直接丢弃带有丢失值的特征向量。本文在数据处理时，采用第二种方式。

由于“振动-应力”数据为不同的量纲和量纲单位，这样的情况会影响数据分析的结果，为了消除指标之间的量纲影响，需要进行数据标准化处理，以解决数据指标之间的可比性。本文采用离差标准化的方法，对清洗后的数据进行线性变换，使结果值映射到 [0，1]之间。其转换函数如式（4）所示。

对待学习数据进行归一化后，就形成了训练所需要的数据集，其数据结构如图4所示，部分数据可视化后如图5所示。

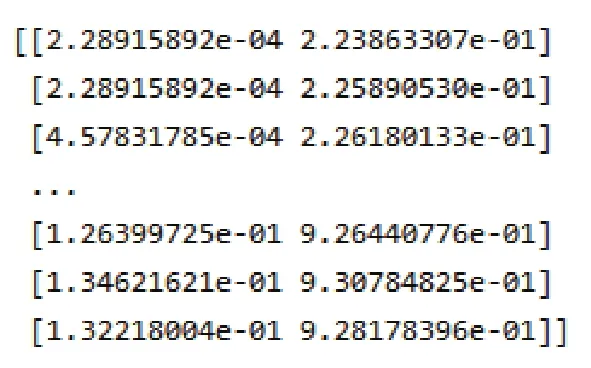
图4 归一化处理后的数据集Figure 4 Normalized data set

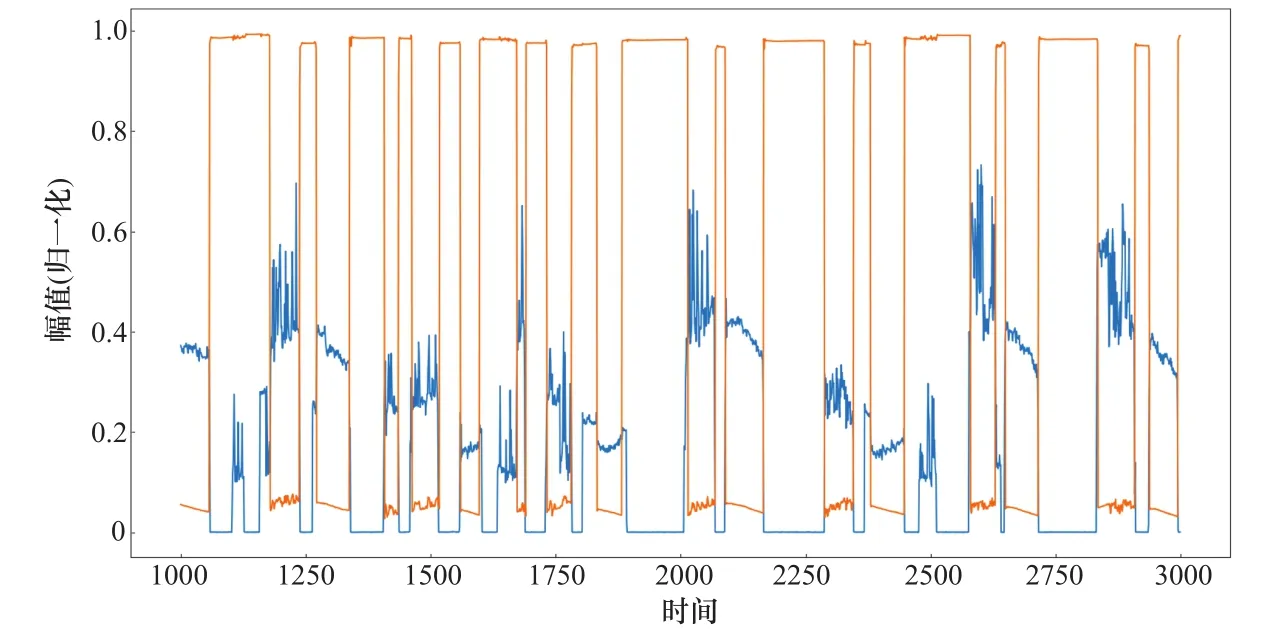
图5 对部分数据集进行可视化Figure 5 Visualization of partial datase

3.3 数据集运算

在获取数据集的基础上调用Sklearn中SVM包里面的OneClassSVM函数来做异常点的检测。该算法支持核函数修改，可以通过调整参数的形式进行选择。

在采用Sklearn对4组数据集进行数据初步分析后，可以获知在不同的运算参数下会有着不一样的误差，通过参数调整，确定使用的运算参数如下：

（1）核函数（kernel）：高斯核。

（2）训练误差（nu）：0.001。

（3）内核系数（kernel coefficient）：0.35。

通过对4组数据集的运算，结果可视化后如图6～图9所示。其中，蓝色曲面围合的点代表正常值，蓝色曲面以外的点为异常点。

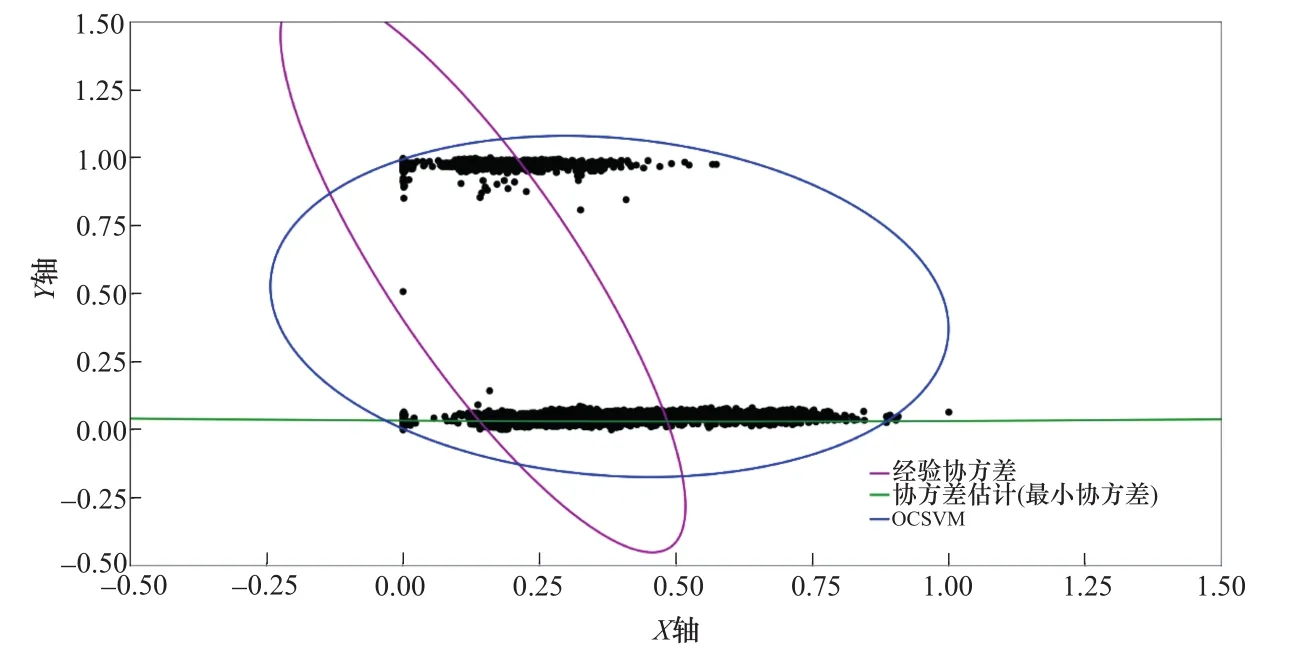
图6 1号支管X轴方向“振动-应力”数据集异常检测Figure 6 Abnormal detection of“vibration-stress”data set in X-axis direction of No.1 branch pipe

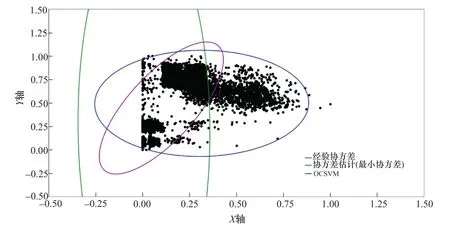
图7 1号支管Y轴方向“振动-应力”数据集异常检测Figure 7 Abnormal detection of“vibration-stress”data set in Y-axis direction of No.1 branch pipe

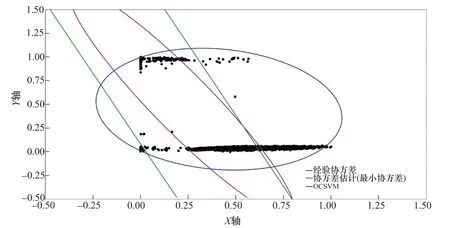
图8 2号支管X轴方向“振动-应力”数据集异常检测Figure 8 Abnormal detection of“vibration-stress”data set in X-axis direction of No.2 branch pipe

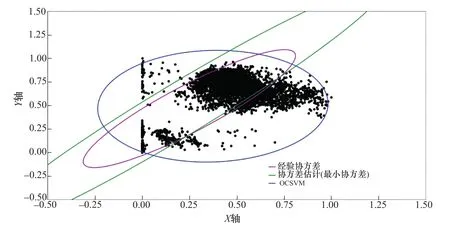
图9 2号支管Y轴方向“振动-应力”数据集异常检测Figure 9 Abnormal detection of“vibration-stress”data set in Y-axis direction of No.2 branch pipe

3.4 异常值分析

从上述可视化结果来看，几乎所有的点均包含在了二维的蓝色曲线以内，但每个数据集的运算结果中也包含一部分离群的点，这是我们设定的0.001系数的训练误差所决定的，将上述四个数据集偏离最大的点进行数据定位后，分析如下：

1号支管X方向“振动-应力”异常坐标点编号为6239，该异常点所处的数据位置如图10所示；1号支管Y方向“振动-应力”异常坐标点编号为9881，该异常点所处的数据位置如图11所示；2号支管X方向“振动-应力”异常坐标点编号为2327，该异常点所处的数据位置如图12所示；2号支管Y方向“振动-应力”异常坐标点编号为2025，该异常点所处的数据位置如图13所示。

图10 1号支管X方向异常点坐标Figure 10 Coordinates of abnormal points in X-axis direction of No.1

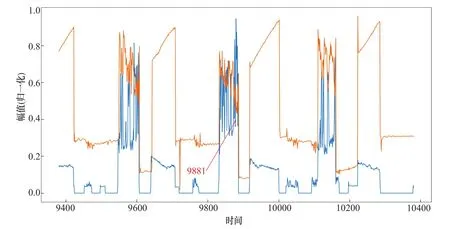
图11 1号支管Y方向异常点坐标Figure 11 Coordinates of abnormal points in Y-axis direction of No.1

图12 2号支管X方向异常点坐标Figure 12 Coordinates of abnormal points in X-axis direction of No.2

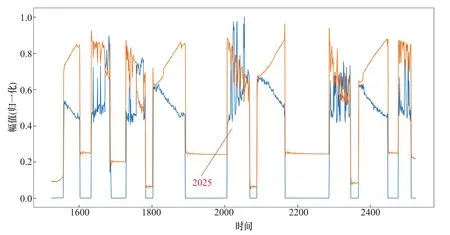
图13 2号支管Y方向异常点坐标Figure 13 Coordinates of abnormal points in Y-axis direction of No.2

上述4个异常点的位置确定后，与压力钢管运行的历史数据时间标签进行对比查看，确定该异常点所指向传感器信息获取的具体时间如下：9月5日20时31分58秒（发电状态）、9月21日20时49分39秒（发电状态）、8月22日19时36分10秒（发电状态）、8月21日20时20分01秒（发电状态）。

4组异常值所处的时间范围集中在晚上20时左右，且设备均处于发电状态。由此可以判断，通过该算法进行计算后，系统具有发现设备异常状态的能力。需要说明的是，本次发现的异常点只是从设备正常运行数据中抽取的，该异常点仅说明了设备此时的工况发生了细微的变化，并不说明设备出现了故障。

4 结语

（1）对于设备的异常检测，可以在考虑数据特征和系统开销的情况下，选择合适的机器学习算法，以达到准确找出异常数据的目的。

（2）聚类问题只是在单一样本数据中发现离群值的一种方法，该方法可以实现离群值的快速检测，但并未标注出离群值所处的风险因子，因此，该方法可以作为小数据集和设备健康监测初期进行的尝试性预测。

（3）正、反两类样本的不平衡造成机器学习算法的分类困难的，当随着设备自身健康数据的积累越来越多，其分类的优化也更加容易。但由于聚类问题随着数据量的增加也会增加系统开销，所以在数据量在不断增大时，可以考虑使用聚类再使用分类器学习归纳其模型，从而达到集群扩展并应用于新增数据的目的。