机械式激光窗口结构设计与防尘罩抗风载能力研究

刘旭堂，黄梦婕，王 伟

(1.中国石油大学（华东）机电工程学院，山东 青岛 266580；2.西交利物浦大学设计学院，江苏 苏州 215123）

引 言

激光发射装置常常在野外恶劣环境中工作［1-2］。窗口是保障激光发射装置正常工作的关键部件，它可以隔绝激光发射系统内外环境，保护内部仪器不受外界风沙的袭击和破坏。目前国内外激光发射窗口主要有晶体窗口和气动正压密封窗口两种［1-3］，晶体窗口成本过于昂贵，气动窗长时间工作会消耗设备大量能源，且容易暴露设备所在位置。设备工作时间通常只有几十秒，而间歇时间从几分钟到几个小时不等，其间气动窗口必须持续工作，以保持警戒状态。为此设计了一套大口径快门式机械密闭窗口，激光发射期间机械窗口打开，气动窗口启动提供正压密封，激光发射间歇时间机械窗口关闭代替气动窗口保护激光发射装置内部设备。防尘罩抗风载能力是窗口的主要设计指标，能否准确计算窗口抗风载能力直接影响到激光发射装置的使用环境和维护标准。目前评估薄板抗风载能力的方式是经验评估和小挠度薄板变形计算［4-5］。经验评估计算偏差较高且缺少稳定性［6］，小挠度薄板计算公式要求薄板变形量不超过自身厚度［7-9］，当风速超过5 m/s时，窗口防尘罩最大变形量就超过自身厚度，模型的计算误差达到20%以上，此时薄板径向薄膜力的影响不能忽略［10-13］。

为准确评估窗口抗风载能力，依据薄板挠曲变形方程建立防尘罩抗风载能力的线性评估模型［14-15］。在板壳变形方程中加入径向薄膜力，建立含有径向拉应力的非线性微分方程［16-18］。利用中心挠度作为摄动参数求解，将非线性边界问题中各待定函数展开为载荷的幂级数（相应系数为未知函数），通过代入原方程、比较载荷的同次幂系数，得到一系列的确定未知函数的线性边界问题［19-20］。进一步求解线性方程组得到挠度与正压载荷、挠度与径向应力间的解析关系。最后获得防尘罩挠曲变形量与正压风载和密封压力的评估模型，该模型可以依据电机参数准确计算防尘罩的最大抗风载能力。

1 窗口的基本结构

窗口基本结构如图1所示。

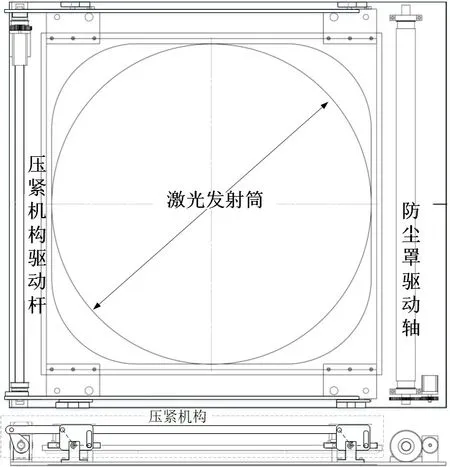
图1 机构整体装配图

窗口主要是由压紧装置和防尘罩收放装置两部分组成。压紧装置主要是由步进电机驱动一个三连杆机构组成，3 个连杆长度一致，倾角相同，运动同步，密封圈通过连接轴与连杆机构相连，连杆机构设有一个滑道，连接轴可以在滑道内移动。该机构的优势是既可以驱动密封压圈向下压紧同时不产生水平移动，此外该机构不完全固定的连接方式可有效避免机构运行过程中的卡滞现象。防尘罩收放装置是通过驱动轴带动同步带完成的，防尘罩一端固定在防尘罩驱动轴上，另一端固定在从动杆上，随驱动轴同步运动。防尘罩材料采用PDFE薄板，表面喷涂一层硅胶，兼具防火、防水和耐环境腐蚀老化的功能。

2 防尘罩挠曲变形的计算分析

窗口抗风载能力是设备的主要设计指标，该指标主要由防尘罩的挠曲变形量、密封压力和防尘罩刚度3个参数决定。激光发射筒的直径即挠曲变形区域直径为600 mm，防尘罩最大变形量不能超过7 mm，否则会影响防尘罩密封效果。假设防尘罩挠曲变形区域外边界和密封压力内边界重合且均为圆形，则防尘罩变形过程可以等效为圆形薄板的挠曲变形，正压风载与风速力学模型如图2 所示，R为风载半径。

图2 防尘罩风载变形示意图

假设正压风载q为均布载荷，则满足以下关系［21］：

式中：CD为风阻系数，Vm为平均风速，ρ为空气密度，q为防尘罩承受正压风载，假设变形过程中薄板厚度不变，在薄板挠度方程中加入径向切应力σr，可以得到薄板大挠度变形方程：

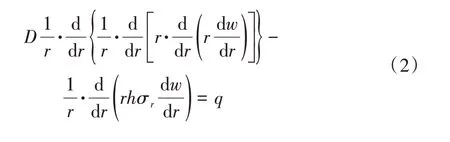
式中：h为薄板的厚度，E为薄板弹性模量，w为挠曲变形量，D为薄板弯曲刚度，r为径向坐标，q为薄板所承受的正压风载。其中式（2）左边第一项主要受到薄板弯曲刚度的影响，而第二项则主要受到薄膜应力影响。当薄板挠曲变形不超过自身厚度时，薄膜应力的影响可以忽略不计。薄板大挠度变形非线性微分方程可以简化为小挠度线性微分方程：

当防尘罩变形量超过自身厚度，薄膜力的影响较大，需利用薄板大挠度变形方程来获得挠曲变形量。薄板大挠度变形方程是非线性微分方程，本文选取摄动法来求解该方程，以中心挠度为摄动参数，假设风载部分为圆形，薄板变形的边界条件简化为：

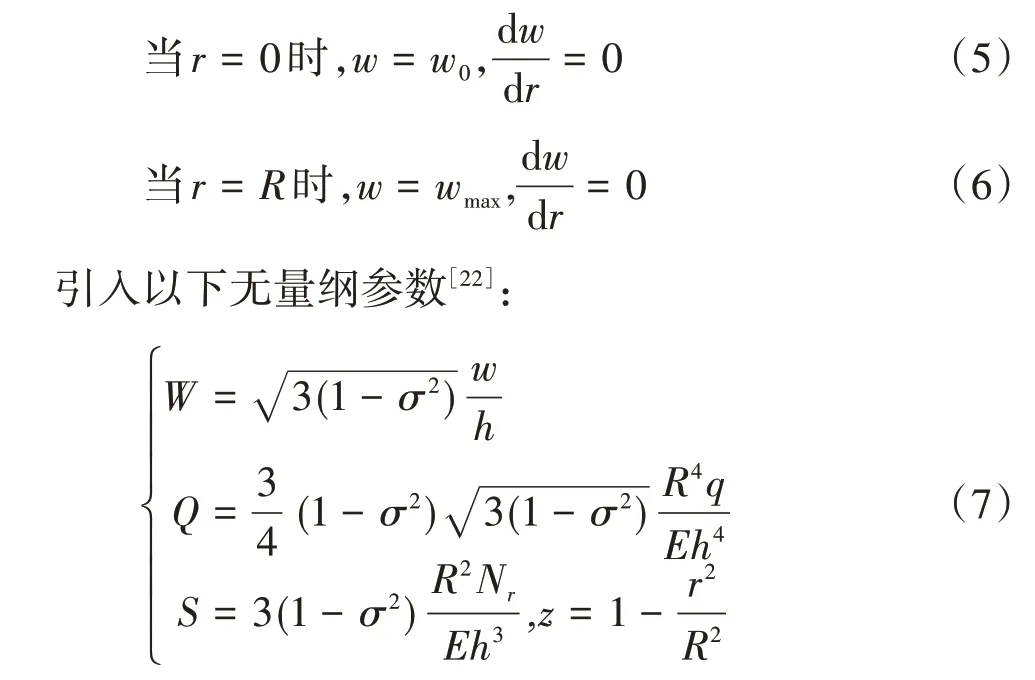
其中：Nr为径向拉应力，σ 为径向切应力，W、Q和S分别为等效挠曲变形量、等效压应力和等效拉应力，z为等效轴向坐标，主要用于评估薄板挠曲变形量、径向压力和径向拉力。薄板大挠度变形微分方程简化为：

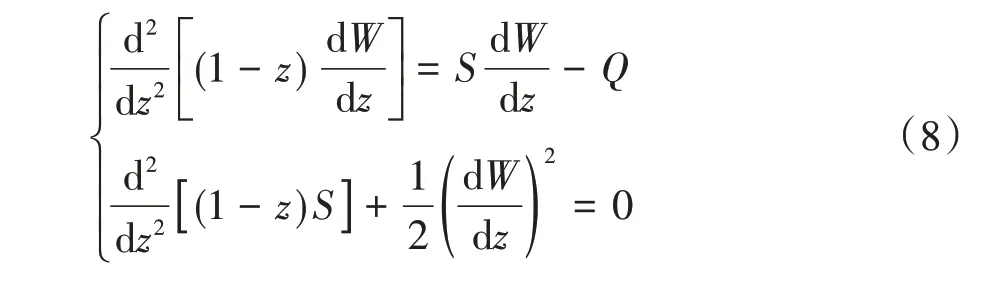
以防尘罩承受风压载荷区域中心的挠曲变形量为求解参数，薄板大挠度变形微分方程可以展开为中心挠度的幂级函数，防尘罩表面等效压应力可以简化为：

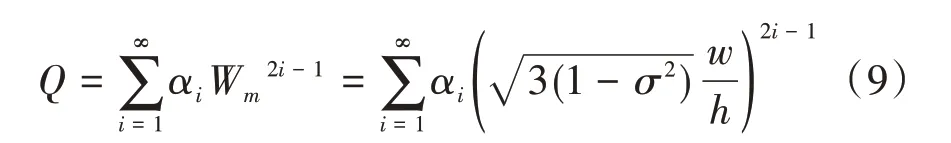
其中：αi为变形系数，i为展开系数，W2i-1m为无量纲参数W沿径向展开式。防尘罩周边区域的等效径向拉应力可以简化为：

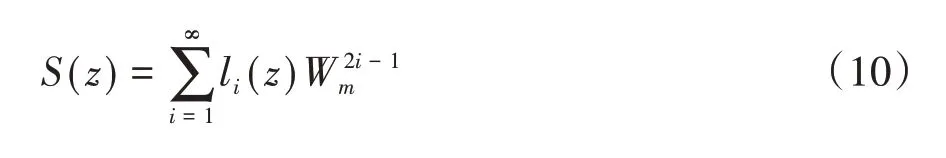
式中：li(z)为需要确定的系数函数，S(z)为无量纲参数S沿轴向展开式。将各系数函数代入式（8）中按照Wm的次数重新组合，可以得到关于系数函数li(z)和系数αi的微分式，代入边界条件可以得到对于不同z值，系数函数li(z)和系数αi的取值。当i≥3时，系数函数li(z)和系数αi小于首项五十分之一，其产生的计算误差较小可以忽略不计。由此可以得到防尘罩等效压应力和径向拉力关于Wm的表达式：

对于防尘罩的任意厚度h，根据式（11）可以确定W(h)与正压风载之间的对应关系，根据式（12）可以获得防尘罩径向载荷与S(h)之间的对应关系。

在窗口的设计使用过程中，防尘罩密封压力产生的径向拉力要远大于防尘罩挠曲变形所产生的径向拉力，对防尘罩径向拉应力积分可以得到径向拉力：

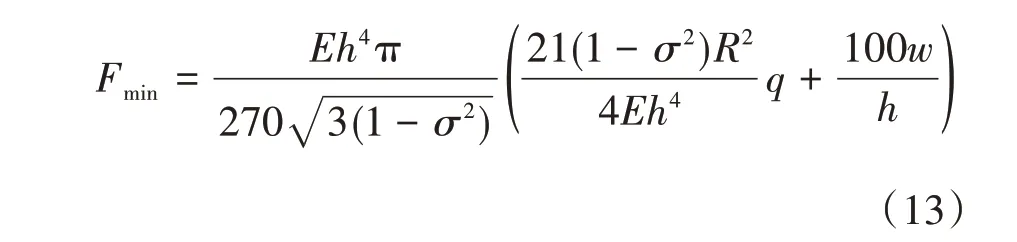
防尘罩径向拉力Fmin是由压紧机构密封压力Fy和防尘罩与密封圈间的摩擦系数μ决定的，即满足：

压紧机构压紧状态时的受力如图3 所示。其中，电机的有效输出扭矩为M，压紧机构的驱动扭矩为M'，受导向杆作用压紧机构只能沿垂直方向运动，压紧状态下夹角α和夹角β均为30°，密封压力忽略摩擦力的作用，可以得到：

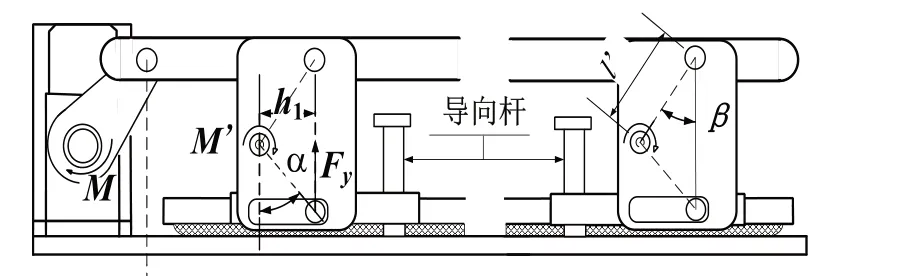
图3 压紧机构受力图

依据压紧机构受力结构可知，防尘罩压紧力Fy主要是由驱动电机输出扭矩决定的，受到密封圈弹性模量E1与压缩行程h2的影响，由式（14）和式（16）可以得到不同风压载荷作用下，电机输出扭矩和密封圈参数的设计要求：

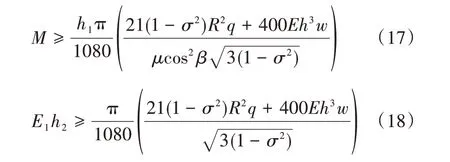
式中：h1为密封圈压缩量。

为准确评估式（17）和式（18）的计算误差，利用有限元软件建立窗口抗风载能力分析模型，假设电机输出扭矩3.5 N·m，当防尘罩厚度为0.8 mm，任意选择正压风速为15 m/s、12 m/s、11 m/s 和10 m/s，防尘罩的防尘罩挠曲变形云图如图4 所示。

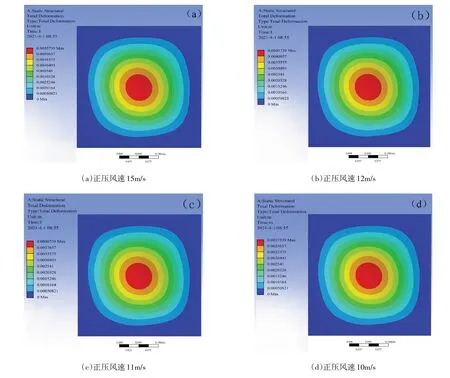
图4 防尘罩挠曲变形量分布

从图4 中可知，防尘罩变形分布规律与评估模型一致，且不随风速变化而发生明显改变，中心变形挠度最大，且变形云图呈圆形分布。边缘挠曲变形量约为0，变形云图分布规律与密封压圈边缘重合，有限元分析结果与评估模型计算结果对比见表1，其中变形计算结果均取小数点后两位。

表1 防尘罩挠曲变形量计算误差对比

从表1 中可见，数值模拟结果会略高于评估模型的计算结果，造成求解误差的主要原因在于：模型边界简化为圆形边界，而出于安装需要实际密封压圈并非完整圆形边界。当风速小于15 m/s 时，随风速增大，评估模型计算结果偏差与有限元分析结果偏差均逐渐增大。误差增大主要原因在于随正压风载的增加，密封压力对挠曲变形的影响逐渐加大，而防尘罩刚度对挠曲变形的影响逐渐降低，改变了防尘罩弯曲刚度和正压风载取值。模型计算偏差变化规律与表1 所示规律相同，当圆形薄板挠曲变形区域直径600 mm，变形量不超过7 mm 时，边界简化导致的计算误差不超过3%。

3 实验测试

建立了如图5 所示的测试方案，利用高速风机模拟正压风载，风机可以输出不超过20 m/s 均布正压气流和负压气流。选取直线测位计测量挠曲变形量，利用皮托管流量计反馈实际风速，防尘罩弯曲刚度变化主要是通过改变防尘罩厚度实现的。驱动电机最大输出扭矩为4.2 N·m，为设备安全考虑，实验统一设置电机输出扭矩为3.5 N·m，窗口开启和关闭时间小于3 s。

图5 窗口风载测试方案

当防尘罩厚度为0.8 mm，风速小于15 m/s 时，防尘罩挠曲变形量的检测结果与理论分析结果见表2。

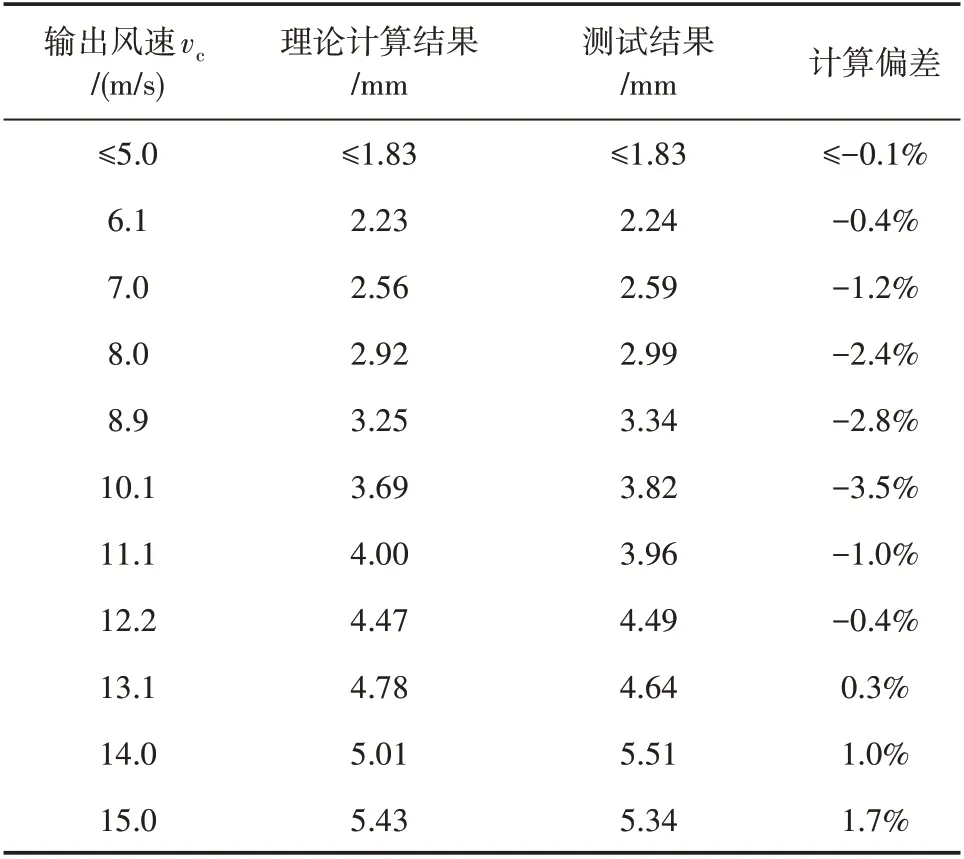
表2 防尘罩挠曲变形量检测结果

由表2 测试结果可知：当风速小于12 m/s 时，实际变形测试结果要略高于理论分析结果，造成计算偏差的主要原因在于建立模型过程中忽略了摩擦力影响。当风速低于10 m/s时，随风速增加，模型计算偏差会逐渐增大，主要由于：摩擦力的作用降低了密封压力，随风速增加密封压力对防尘罩挠曲变形量的影响会逐渐加大，因此计算偏差也随之增大。当风速超过10 m/s时，随风速增加，模型计算偏差绝对值反而会逐渐减少，主要由于：正压风载会作用在密封压圈以外的防尘罩上，风压载荷对防尘罩形成一定的密封压力，这部分密封压力抵消了部分由于摩擦力作用而导致密封压力减小的影响。当风速大于12 m/s 时，评估模型计算偏差由负转正并逐渐增大。

相关测试结果表明：当风速低于15 m/s时，评估模型计算偏差绝对值小于3.5%，评估模型的计算精度比现有评估方式高16%以上，最大挠曲变形量是5.34 mm，低于窗口设计要求的7 mm。本文所设计机械窗口的最大抗风载能力达到15 m/s，气动窗口最大抗风载能力只有10 m/s，因此本文所设计的机械窗口最大抗风载能力远高于目前所使用的气动窗口。

当窗口直径为600 mm，挠曲变形量不超过7 mm 时，选取不同风压载荷和防尘罩厚度，测试结果与式（18）分析结果最大偏差对比见表3。

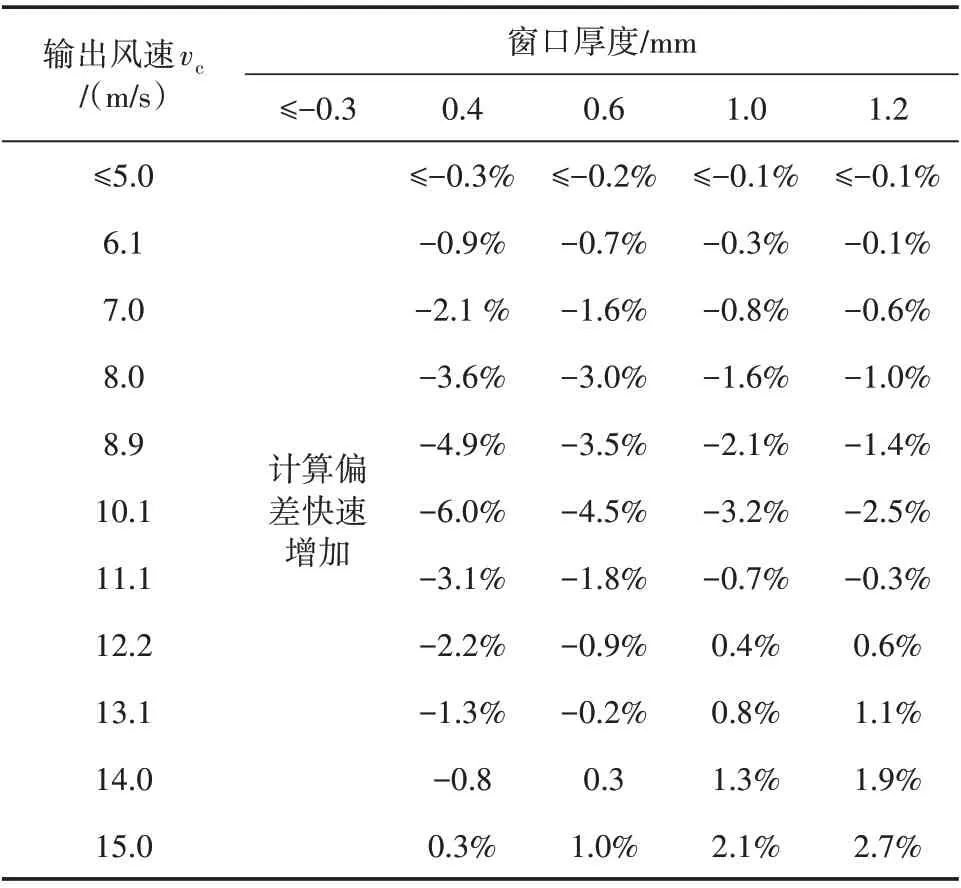
表3 不同窗口厚度下防尘罩挠曲变形量最大计算偏差

由表3可知，改变防尘罩厚度和正压风载以后，式（18）分析结果最大偏差会产生一定波动，但对于常用厚度的几类PDFE 薄板，评估模型最大计算偏差保持在6%以内。当防尘罩弯曲刚度不变，随风速增加，计算结果误差变化规律与表2相同；当风速一定，防尘罩弯曲刚度增大时，计算误差会小范围降低，当薄板厚度低于0.4 mm 时，评估模型计算偏差快速增加，主要是因为防尘罩厚度过低，造成式（18）中弯曲刚度对抗风载能力的影响比重过低，防尘罩表现出明显的薄膜力学特性［21］。

此外，当防尘罩厚度达到1.2 mm 时，最大抗风载能力超过20 m/s，此时挠曲变形量小于6 mm，满足了所有靶场和野外环境的设计要求，使激光发射系统的环境适应能力的得到了极大的提高，同时降低了气动窗口90%的能源消耗。综上可知：当窗口口径等于600 mm，风速低于15 m/s，防尘罩厚度不低于0.4 mm 时，窗口抗风载能力计算模型最大计算误差均小于6%，比现有评估模型高出14%以上，机械窗口最大抗风载能力比气动窗口高10 m/s，计算偏差的降低有效提高了激光发射系统内部洁净度的计算精度，挠曲变形量的减小可以有效降低设备内部灰尘含量，减轻因灰尘附着造成的激光烧蚀，提高了设备的使用寿命，降低了设备的维护难度。

4 结束语

所设计窗口可以极大地提高激光发射系统的抗风载能力、环境适应能力和使用寿命，降低设备的维护成本，但在实际计算窗口抗风载能力过程中，评估模型需要考虑两个方面的影响：

首先，评估模型外边界与实际边界不重合，使评估结果产生偏差，当激光发射筒直径是600 mm，挠曲变形量不超过7 mm时，计算偏差不超过3%；

其次，由于机构内部摩擦力的影响，评估模型与窗口实际抗风载能力存在偏差，当激光发射筒直径为600 mm，挠曲变形量不超过7 mm 时，窗口内部机构摩擦和边界不重合造成的耦合偏差不超过6%。