THE VALUE DISTRIBUTION OF GAUSS MAPS OF IMMERSED HARMONIC SURFACES WITH RAMIFICATION*

Zhixue LIU (刘志学) Yezhou LI (李叶舟)

School of Science，Beijing University of Posts and Telecommunications，Beijing 100876，China E-mail:zxliumath@bupt.edu.cn;yezhouli@bupt.edu.cn

Xingdi CHEN (陈行堤)

School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China E-mail:chxtt@hqu.edu.cn

Abstract Motivated by the result of Chen-Liu-Ru[1]，we investigate the value distribution properties for the generalized Gauss maps of weakly complete harmonic surfaces immersed in Rn with ramification，which can be seen as a generalization of the results in the case of the minimal surfaces.In addition，we give an estimate of the Gauss curvature for the K-quasiconfomal harmonic surfaces whose generalized Gauss map is ramified over a set of hyperplanes.

Key words value distribution;harmonic surfaces;quasiconformal mappings;conformal metric，Gauss map

1 Introduction

In this paper，we study the value distribution properties for a Gauss map of the immersed harmonic surfaces in Rn.This study was initiated by R.Osserman and S.S.Chern[2-4]，who gave attention to the case of complete minimal surfaces immersed in Rn.Over the last few decades，many important works have been carried out in this area (see[1，5-11])，including those by Chen-Liu-Ru[1]，Xavier[5]，Ru[7，8]，Fujimoto[9]and Osserman-Ru[10].Osserman[12]showed that the Gauss map of a complete non-fl at minimal surface in R3cannot omit a set of positive logarithmic capacity in Q1(C).Subsequently，Chern and Osserman[3]showed that the Gauss map of a non-fl at complete minimal surface in Rnintersects a dense set of hyperplanes.In 1981，Xavier[5]showed that the Gauss map of a non-fl at complete minimal surface in R3cannot omit seven points of the sphere.In 1988，Fujimoto[13]proved Nirenberg’s conjecture that the Gauss map of a complete non-fl at minimal surface in R3，can omit at most 4 points，and the bound is sharp.

Based on an earlier result of Fujimoto[14]，Ru proved the following result (see also[14，Theorem 1.1]):

Theorem 1.1([7，Corollary]) Let M be a complete minimal surface immersed in Rn.Then the generalized Gauss map Φ can omit at most n (n+1)/2 hyperplanes in Pn-1(C) located in general position.

Ros[15]gave a simple and unified proof of the curvature estimates for stable minimal surfaces and for minimal surfaces whose Gauss map image omits five points.Later，Osserman and Ru[10]obtained a version of the curvature estimates for minimal surfaces in a higher dimension.

Theorem 1.2([10，Theorem 1.1]) Let X:M→Rnbe a minimal surface immersed in Rn.Suppose that its generalized Gauss map Φ omits more thanhyperplanes in Pn-1(C)，located in general position.Then there exists a constant C，depending on the set of omitted hyperplanes，but not the surface，such that

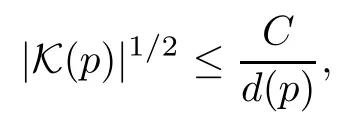
where K (p) is the Gauss curvature of the surface at p，and d (p) is the geodesic distance from p to the boundary of M.

As early as the late 60s，Milnor[16，17]started to consider whether this theory carries over in an interesting way to the larger class of harmonically immersed surfaces;some similar results to those above were obtained (see[1，18-20]).

Let X:M→Rn(n≥3) be a regular and an immersion map，where M is a smooth oriented two-manifold without a boundary.The surface X (M) is called an immersed harmonic surface if X is harmonic.We may consider M as a Riemann surface by associating a holomorphic local coordinate z=u+iv with each local coordinate (u，v) of M.It is well-known that X is harmonic if and only if

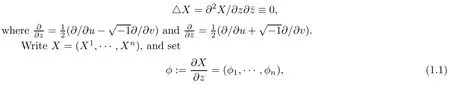
where φi=for i=1，···，n and φiare only locally defined.We know that X is harmonic if and only if φiare holomorphic for all i=1，···，n.Let Φi:=φidz be some holomorphic one-forms，obviously Φiare globally defined on M and so the holomorphic map Φ:=[Φ1:···:Φn]:M→Pn-1(C) is well-defined on M;here we call it the generalized Gauss map of the harmonic surface X (M).

Milnor[20]observed that the generalized Gauss map Φ，instead of the Gauss map n，carries value distribution properties similar to the Gauss map n in the minimal surface case.We recall the following result，due to T.K.Milnor[20](see also Theorem 2.1 in[21]):

Theorem 1.3([20，Theorem 3]) Let X=(X1，···，Xn):M→Rnbe a complete immersed harmonic surface with the induced metric，where M is a Riemann surface.Let Φ=[Φ1:···:Φn]:M→Pn-1(C)，where Φi:=dz for i=1，···，n，be the generalized Gauss map.Then either X (M) is a 2-plane or else Φ(M) comes arbitrarily close to every hyperplane=0 in Pn-1(C).

Chen et al.[1]investigated the value distribution properties for the generalized Gauss map Φ of an immersed harmonic surface;this obtained a result similar to that of Fujimoto and Ru in the minimal surfaces case.

Theorem 1.4([1]) Let M be an open Riemann surface and X=(X1，···，Xn):M→Rnbe a harmonic immersion.Let Φ:M→Pn-1(C) be the generalized Gauss map.Assume that X is weakly complete with respect to the reduced metric.If Φ omits more thanhyperplanes in Pn-1(C) in general position，then X (M) lies in a 2-plane.

Not all of these properties will have resonable counterparts;minimal surfaces are enormously special.In this paper we obtain some value distribution properties for the generalized Gauss map of the immersed harmonic surfaces in Rnwith ramification.

Here，we use some notations and results of the geometric orbifold as shown in[22].An orbifold consists of a compact irreducible complex space together with a Weil Q-divisor.Let (X，D) be an orbifold with D:=，where mj∈N∪{∞}are multiplicities and Hjare distinct hyperplanes.One also says that D is an orbifold structure on X.An orbifold can be regarded as a complex space endowed with an additional structure in the form of a certain Weil Q-divisor.A holomorphic map f from the unit disk Δ={z∈C:|z|＜1}to an orbifold (X，D) is an orbifold morphism if f (Δ)/⊂supp (D) and multz(f*Hj)≥mjfor all j and z∈Δ with f (z)∈supp (Hj).

2 Main Results

Let ds2be the metric on M induced through X from the standard inner product on Rn.In terms of local coordinate (u，v)，let z=u+，ds2be given in the following form:

where

In particular，if h≡0，then ds2=2||φ||2|dz|2.Here we say that (u，v) is an isothermal coordinate of the surface M.It is well-known that X is minimal if

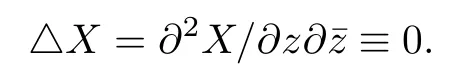
Let Γ:=2‖φ‖2|dz|2be the associated conformal metric of ds2defined in (2.1).Since|h|≤‖φ‖2，it follows from (2.1) that the associated conformal metric Γ is complete if ds2is complete (see also Lemma 1 in[23]).The metric ds2is said to be weakly complete if the associated conformal metric Γ is complete.If ds2is (weakly) complete，then we also say the surface M is (weakly) complete.

Let Φ=[φ0:···:φn-1]:Δ→Pn-1(C) be a holomorphic map and let H:={[z0:···:zn-1]|a0z0+···+an-1zn-1=0}be a hyperplane in Pn-1(C).We say that Φ is ramified over H with multiplicities of at least m if all zeros of the holomorphic functionhave orders of at least m，whereis a reduced representation of Φ.Note that we always say that Φ is ramified over Hjwith multiplicity∞if Φ omits Hj.

One of our main results is as follows:

Theorem 2.1Let M be an open Riemann surface and X=(X1，···，Xn):M→Rnbe a harmonic immersion.Let Φ:M→Pn-1(C) be the generalized Gauss map.Assume that X (M) is weakly complete with respect to the reduced metric.If there are q hyperplanes H1，H2，···，Hq⊂Pn-1(C) located in general position such that the generalized Gauss map Φ of M is ramified over Hjwith a multiplicity of at least mjfor each j∈{1，2，···，q}，and if

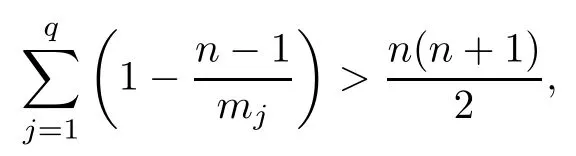
then X (M) lies in a 2-plane.

Remark 2.2Under the same assumptions as in Theorem 2.1，and as discussed in the proof of Theorem 2.1，one knows that the generalized Gauss map Φ is a constant map.Thus，Theorem 2.1 implies Theorem 1.1.

In particular，we study the value distribution theory for quasiconformal harmonic surfaces immersed in R3，and an estimate of the Gauss curvature is established.We briefly introduce the definition of a K-quasiconformal harmonic surface given by Kalaj[24](see also[1，18]).

Let M be an open Riemann surface and let X=(X1，X2，X3):M→R3be a harmonic immersion.Write

‖∇X‖2=4‖φ‖2，

where‖∇X‖2is the Hilbert-Schmidt norm defined by‖∇X‖2:=‖∂X/∂u‖2+‖∂X/∂v‖2.Also，the Jacobian of X is given by

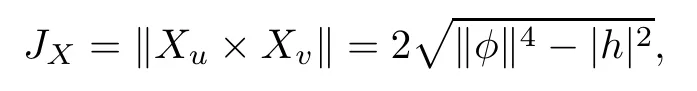
where φ is given by (1.1)，and h and‖φ‖are defined by (2.2).

An immersion X=(X1，X2，X3):M→R3is called K-quasiconformal if it satisfies the inequality

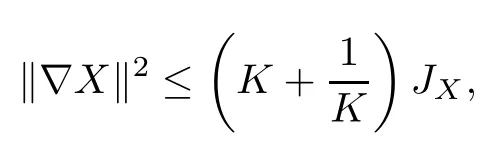
which is equivalent to

If K=1，then the above inequality yields the following results:

|Xu|=|Xv|and Xu·Xv=0.

Here we say that X is an isothermal parametrization (isothermal coordinate) of the surface M.If a Riemann surface M admits a K-quasiconformal harmonic immersion X into R3，X is a K-quasiconformal harmonic immersion，and we call such a surface a K-quasiconformal harmonic surface.

By building a relation between Gauss curvature (intrinsic curvature) and curvature with respect to the associated conformal metric Γ，we prove the following result:

Theorem 2.3Let M be an open Riemann surface and take a K-quasiconformal harmonic immersion X=(X1，X2，X3):M→R3satisfying that there exists a constant η(0≤η＜1) such that

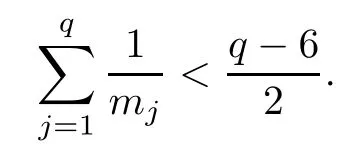
Then there exists a constant C depending on the set of hyperplanes，but not the surface，such that

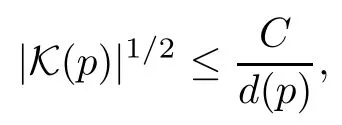
where K (p) is the Gauss curvature of the surface at p，and d (p) is the geodesic distance from p to the boundary of M with respect to the induced metric.

3 Basic Notions and Auxiliary Results

In order to prove our main theorems，we need to introduce some basic notations and some auxiliary results (see also[1]).

Let H={[z0:z1:···:zk]|a0z0+···+akzk=0}be a hyperplane in Pk(C);here a=(a0，···，ak)∈Ck+1{0}is called the normal vector associated to H.Hyperplanes H1，···，Hqare said to be in n-subgeneral position (with n≥k) if and only if，for every injective map μ:{0，1，···，n}→{1，···，q}，the linear span of those corresponding normal vectors aμ(0)，···，aμ(n)is Ck+1.When n=k，then we just say that H1，···，Hqare in general position in Pk(C).It is clear that if hyperplanes H1，···，Hqin Pn(C) are in general position，then，for k≤n，and regarding Pk(C)⊂Pn(C)，the restricted hyperplanes H1∩Pk(C)，···，Hq∩Pk(C) are in n-subgeneral position.

For holomorphic functions f0，f1，···，fk，we say that

is the Wronskian of f0，f1，···，fk.

For a hyperplane Hjin Pk(C) with the normal vector aj=(aj0，···，ajk)，we define，for 0≤s≤k，1≤j≤q，

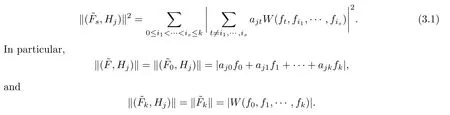
If F is linearly non-degenerate，then0 for all 0≤s≤k and 1≤j≤q.Indeed，if0 for some s and j，then

for all i1，···，is.This implies thatare linearly dependent，which contradicts the linear non-degeneracy of F.

We need the following lemmas:

Lemma 3.1([25，26]) If a k-nondegenerate holomorphic map from C to Pn(C) is ramified over hyperplanes Hj(1≤j≤q) with a multiplicity of at least mj，where Hjare in general position，then

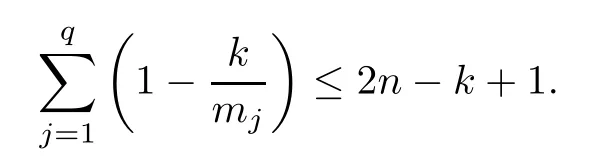
Lemma 3.2([1，Lemma 3.1]) Let X=(X1，···，Xn):M→Rnbe an immersed harmonic surface with the induced metric，where M is a Riemann surface.Let Φ=[Φ1:···:Φn]:M→Pn-1(C)，where Φi:=is the generalized Gauss map.If Φ is constant，then X (M) lies in a 2-plane.

Lemma 3.3([27，Proposition 10]) Let ω be a Hermitian metric on X compact.Assuming that the orbifold (X，D) is hyperbolic and hyperbolically imbedded in X，then the set of all orbifold morphisms f:Δ→(X，D) is relatively compact in Hol (Δ，X)，where Hol (Δ，X) denotes the set of all holomorphic maps of Δ into X.

Lemma 3.4([22，Proposition 7]) Let fn:(X，Δ)→(X′，Δ′) be a sequence of orbifold morphisms.Assume that{fn}，regarded as a sequence of holomorphic maps from X to X′，converges locally uniformly to a holomorphic map f:X→X′.Then either f (X)⊂Supp (Δ′)，or f is an orbifold morphism from (X，Δ) to (X′，Δ′).

Lemma 3.5([10，Lemma 2.2]) Letbe a sequence of conformal metrics on the unit disc Δ whose curvatures satisfy-1≤Kl≤0.Suppose that Δ is a geodesic disk of radius Rlwith respect to the metric，where Rl→∞，and that the metricconverges，uniformly on compact sets，to a metric ds2.Then all distances to the origin with respect to ds2are greater than or equal to the corresponding hyperbolic distances in Δ.In particular，ds2is complete.

Lemma 3.6([28，29]) Letbe a set of hyperplanes in Pk(C) in n-subgeneral position.Then there exist some functions ϖ(j) and a number θ＞0 such that

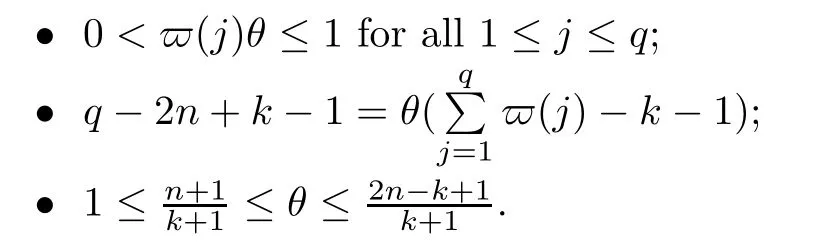
Here ϖ(j) are called the Nochka weights associated to the hyperplanes Hj(1≤j≤q).

Lemma 3.7([9，Lemma 1.6.7]) Let dσ2be a conformal flat metric on an open Riemann surface M.Then for each point p∈M，there exists a local diffeomorphism Ψ of a disk ΔR={w∈C||w|＜R}(0＜R≤∞) onto an open neighborhood of p with Ψ(0)=p such that Ψ is local isometry (i.e.，the pullback Ψ*(dσ2) is equal to the standard Euclidean metricon ΔR)，and there exists a point a0with|a0|=1 and the Ψ-imageof the line={w=a0t:0＜t＜R}is divergent in M.

The following result，obtained by Ru，plays a important role in the proof of Theorem 2.1:

Lemma 3.8([8，Main Lemma]) Let F=[f0:···:fk]:ΔR→Pk(C) be a non-degenerate holomorphic map，let H1，H2，···，Hqbe hyperplanes in Pk(C) in n-subgeneral position，and let ϖ(j) be their Nochka weights.Take a reduced representation=(f0，f1，···，fk) of F.If F is ramified over Hjwith a multiplicity of at least mjfor each j∈{1，2，···，q}and

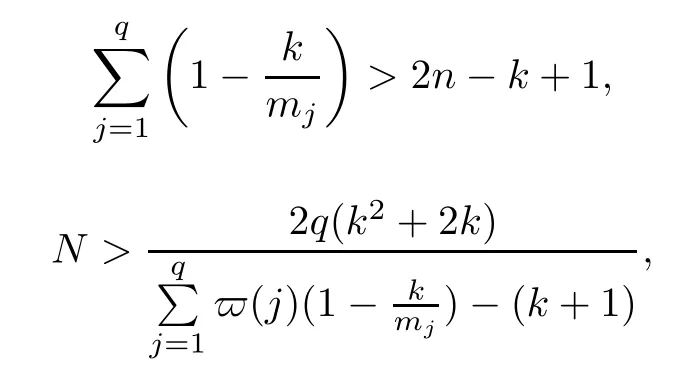
then there exists a positive constant C such that

4 Proofs of the Main Results

4.1 The proof of Theorem 2.1

Based on a similar argument as to that in[1，8]，we start to prove Theorem 2.1.Here，the details for the proof will be shown for the convenience of the reader.

By taking the universal cover of M if necessary，one can assume that M is simply connected.It follows from the uniformization theorem that M is conformally equivalent to the unit disc Δ or C.We claim that Φ is constant map.If not，a contradiction will be derived.

For the case where M is the complex plane C，one can conclude from Lemma 3.1 that Φ is a constant map.For the other case where M is the unit disc Δ，if Φ is not a constant，then there exists k (1≤k≤n-1) such that the image of Φ is contained in Pk(C)⊂Pn-1(C)，but not in any subspace whose dimension is lower than k.In other words，Φ can be regarded as a linearly nondegenerate map from Δ into Pk(C).Letting=(φ0，φ1，···，φk) be a reduced representation of Φ，by the assumption，the metricis complete.Let:=Hj∩Pk(C)，1≤j≤q.Obviously，hyperplanesare in (n-1)-subgeneral position in Pk(C).Furthermore，one may assume thatare given by

always holds for any 1≤k≤n-1，we get that

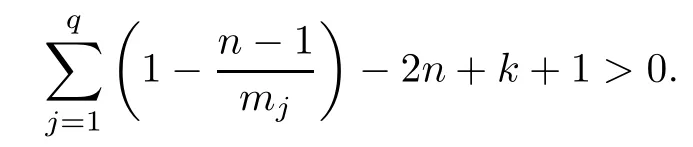
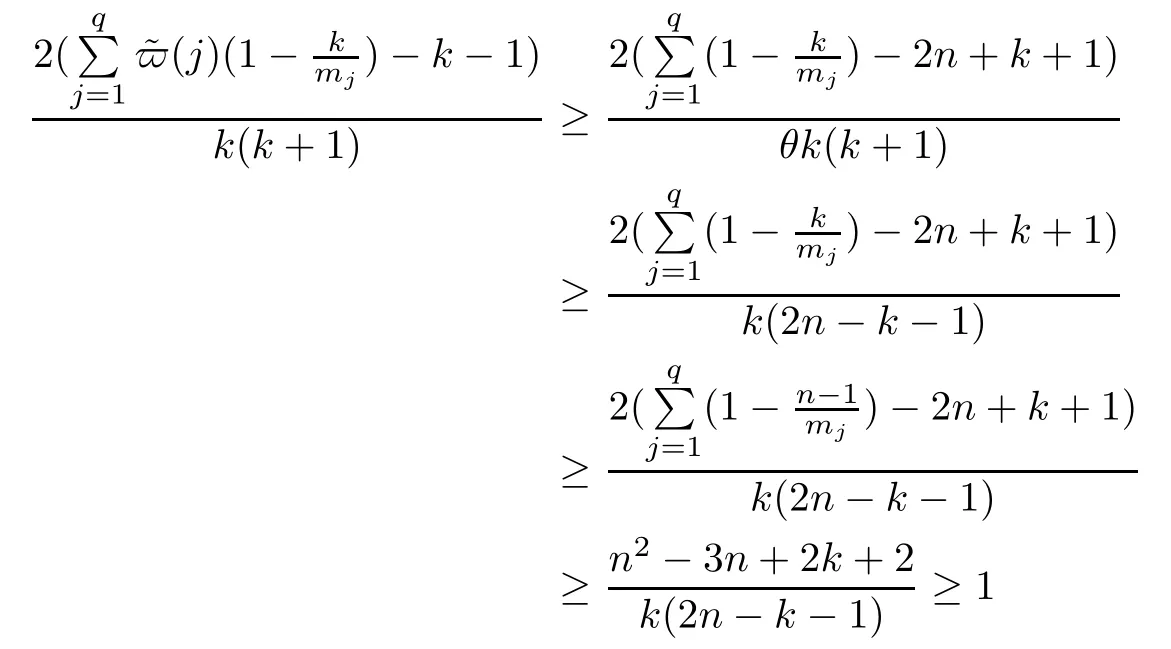
holds for all 1≤k≤n-1.

Choose some N such that

which，together，imply that

0＜τ＜1，0＜NA (1-τ)＜4.

Since Φ:Δ→Pk(C) is linearly non-degenerate，none of the，0≤s≤k，1≤j≤q vanishes identically.Thus，by (3.1)，for eachthere exist i1，i2，···，issuch that

does not vanish identically.Here，let ξj0=.Note that every ξjsis a holomorphic function and has only isolated zeros.

We define a new metric

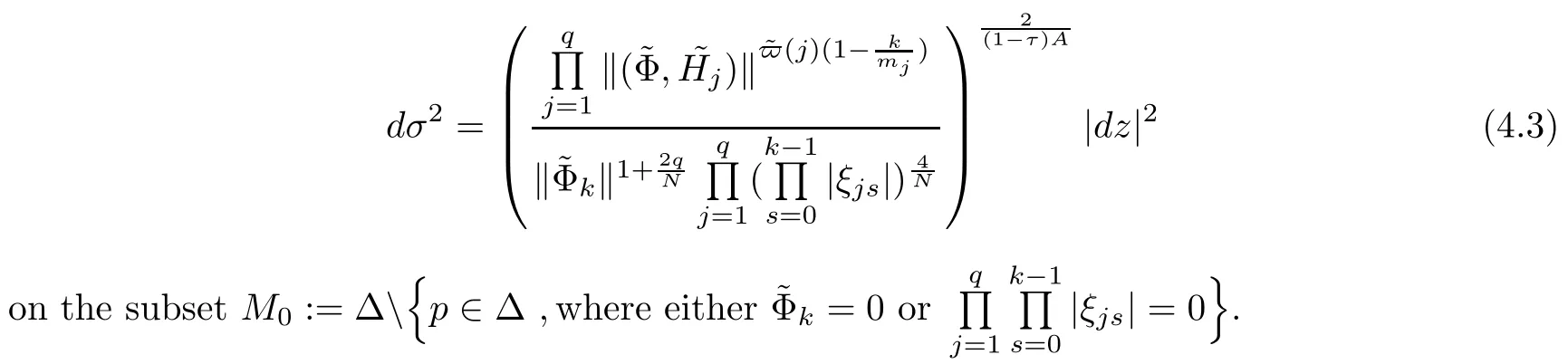
Notice that dσ2is a flat metric on M0.Fixing a point p0∈M0，by Lemma 3.7，there exists a local diffeomorphism Ψ of a disk ΔR={w∈C:|w|＜R}(0＜R≤∞) onto an open neighborhood of p0with Ψ(0)=p0such that Ψ is a local isometry.Furthermore，there exists a point a0with|a0|=1，such that the Ψ-imageof the line={w=a0t:0＜t＜R}is divergent in M0.

By Lemma 3.1，one has that Φ is a constant for the case of R=∞，which is a contradiction.Hence，we know that R＜∞.

Define some functions on{w||w|＜R}as

fs(w):=φs(Ψ(w))(0≤s≤k)，

and F (w):=(f0(w)，f1(w)，···，fk(w)).For 1≤j≤q，0≤s≤k，we define

(F，Hj):=aj0f0+···+ajkfk，Fk:=W (f0，f1，···，fk)

and

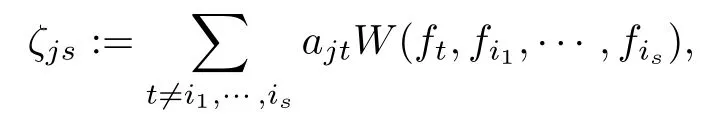
where (i1，···，is) is the index in the definition of ξjsin (4.2).Noticing the fact that，for 0≤s≤k，

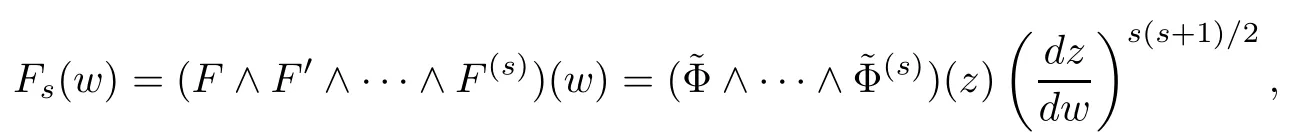
we have，from (4.3)，that

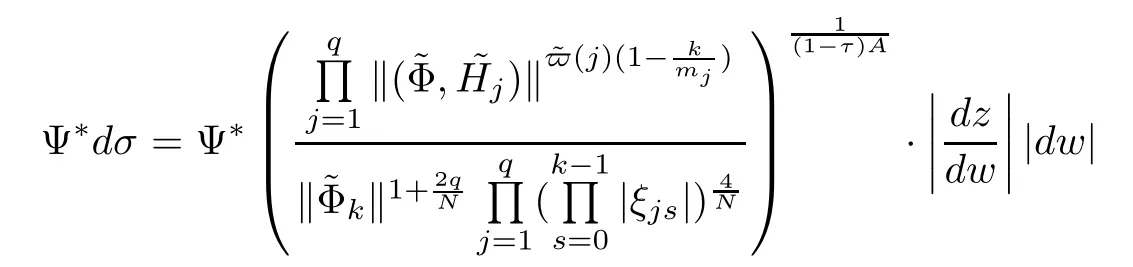
Using the isometry property of Ψ，i.e.，|dw|=Ψ*dσ，we get that

In the above inequality，we use the fact that|ζjs|≤for all 0≤s≤k，1≤j≤q.Noticing that 0＜λ＜1，we conclude from Lemma 3.8 that

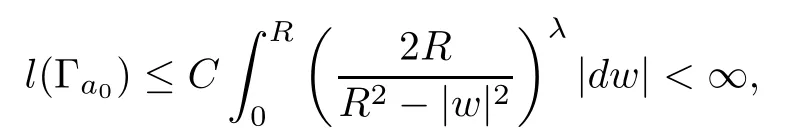
which contradicts the completeness of the metric.Thus，Φ is a constant map.

To prove that X (M) lies in a 2-plane，we denote by K (Γ) the Gauss curvature with respect to the associated conformal metric Γ:=.Then

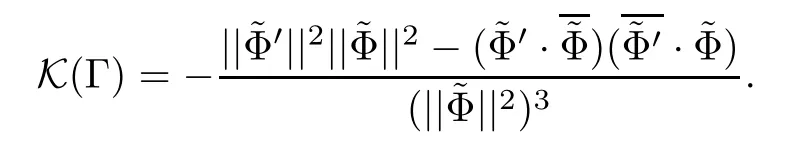
Since Φ is constant，a reduced representationof Φ can be assumed as=(φ0，b1φ0···，bkφ0)，where bj(1≤j≤k) are some complex numbers.Thus，K (Γ)≡0 can be verified.By Lemma 3.2，X (M) lies in a 2-plane.We have thus completed the proof of Theorem 2.1.

4.2 The proof of Theorem 2.3

Inspired by Lemma 3.2 in[10]，the following Proposition can be verified directly by the same argument as to that in[30]，which plays a central role in the proof of Theorem 2.3(here we omit the details for the proof):

Proposition 4.1Let M be an open simply connected Riemann surface and let Φ(l):M→P2(C) be a sequence of holomorphic maps.Fix a globally reduced representation=of Φ(l)(such a representation exists because M is simply connected) and let.Define a sequence of the conformal metricson M as follows:

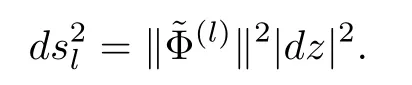
Denote by Klthe Gauss curvature of M with respect to the above metric.Assume that{Φ(l)}converges to a nonconstant holomorphic map φ uniformly on every compact subset of M and that{|Kl|}is uniformly bounded.Then

(i) either there is a subsequenceof{Kl}which converges to zero or

(ii) for each 0≤j≤2，there exists a subsequencewhich converges to a holomorphic function hjon M.Furthermore，h0，h1，h2have no common zeros.

We start by proving Theorem 2.3.

Let ds2be the metric on M induced through X from the standard inner product on R3.In terms of local coordinate (u，v)，ds2is given by

ds2=Edu2+2Fdudv+Gdv2，

with

E=Xu·Xu，F=Xu·Xv，G=Xv·Xv.

The second fundamental form can be shown as

II (n)=Ldu2+2Mdudv+Ndv2，

with

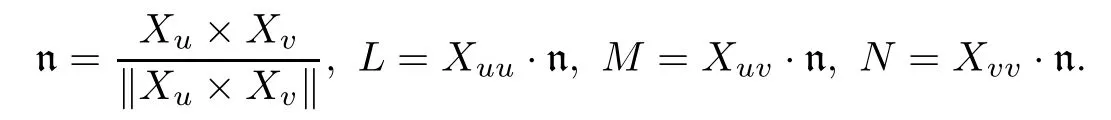
Furthermore，we have

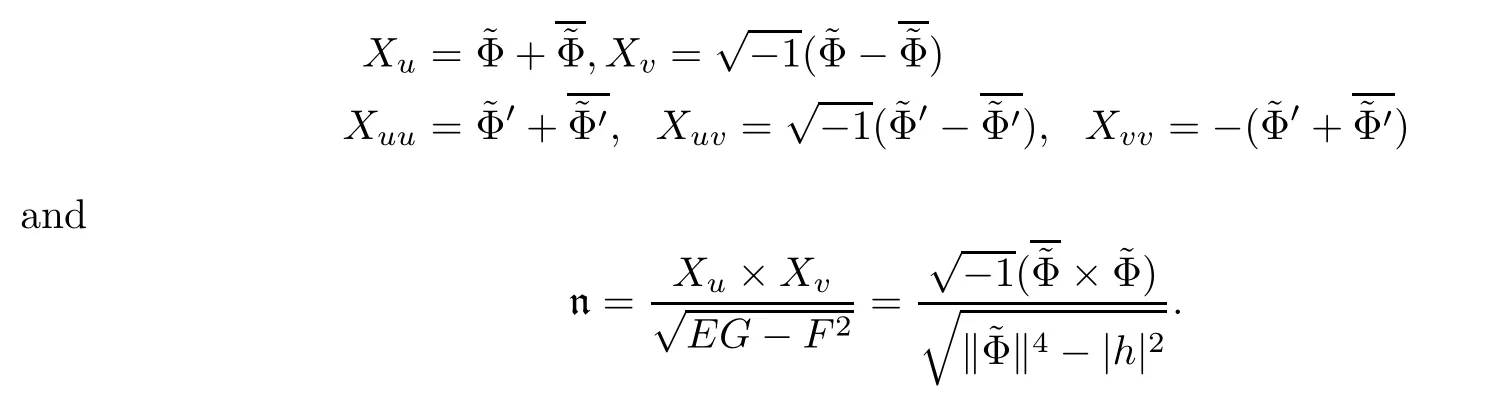
Denoting by K (p) the Gauss curvature of the surface at p with respect to the induced metric ds2above，one has the following expression for K (p):

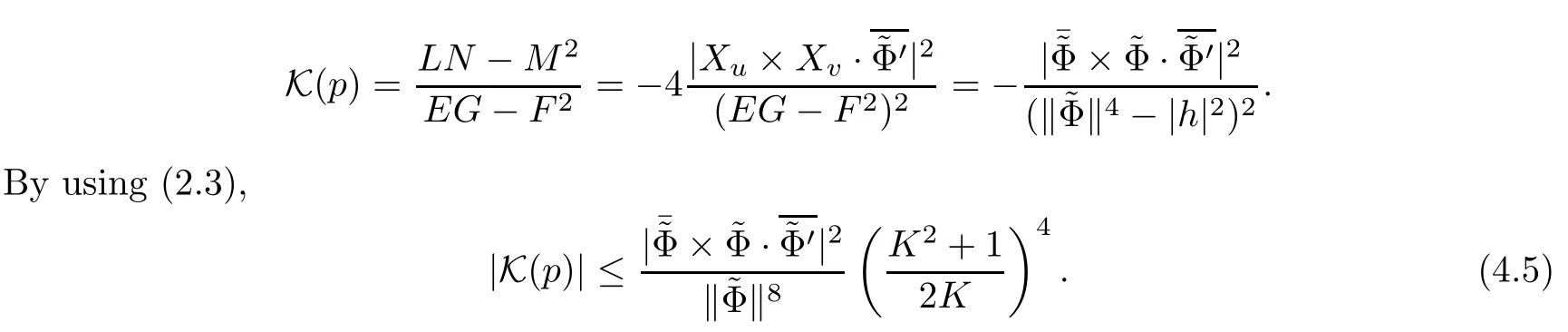
On the other hand，we denote by K (Γ) the Gauss curvature with respect to the associated conformal metric Γ:=and

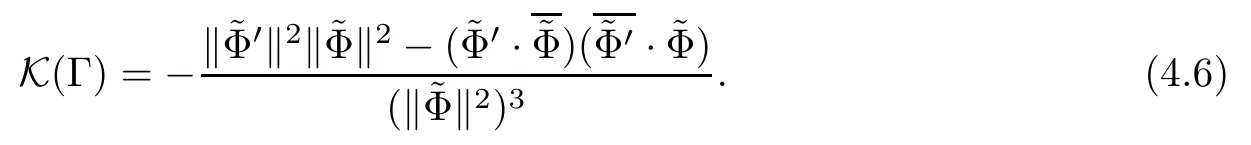
Combining (4.5) and (4.6)，one has the estimation

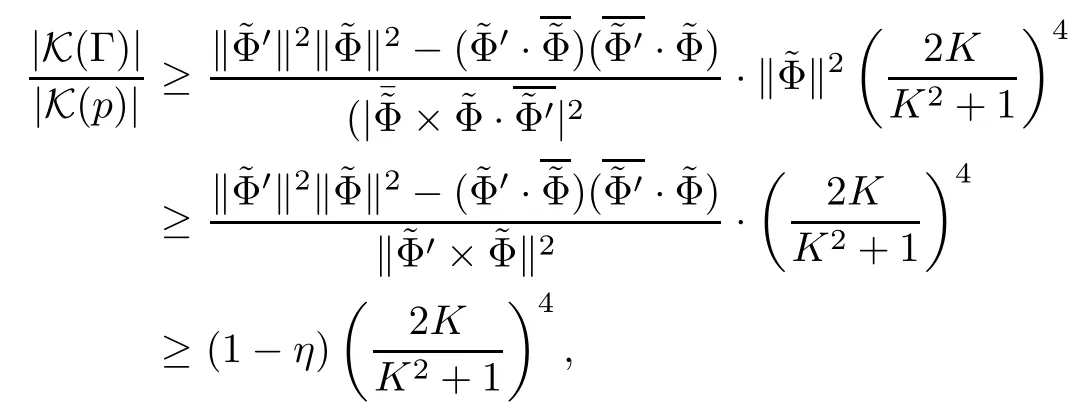
which is equivalent to

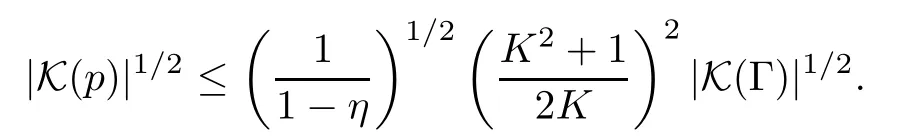
Moreover，one has，by (2.2)，that ds2≤;namely，d (p)≤.It thus remains to prove that there exists a positive number C0such that

For the case that X (M) is weakly complete with respect to the induced metric，i.e.，dΓ(p)=∞holds for all p∈M，by Theorem 2.1 we know that the generalized Gauss map Φ is a constant and that|K (Γ)|1/2=0.Hence (4.2) is a trivial result.We may assume that the associate conformal metric Γ is not complete on M.

To prove (4.2)，we consider an open Riemann surface M endowed with a conformal metric Γ=.If (4.2) does not hold，one can construct a sequence of open Riemann surfaces Ml，points pl∈Ml，and a sequence of the holomorphic map Φ(l):Ml→P2(C) such that→∞，where Kldenotes the Gauss curvature of the surface Mlwith respect to the metricis a reduced representation of Φ(l)，andis the geodesic distance from plto the boundary of Mlwith respect to the conformal metric Γl.Let H1，H2，···，Hq⊂P2(C) be hyperplanes given in Theorem 2.3.Assume that Φ(l)is ramified over Hjwith a multiplicity of at least mjfor each j∈{1，2，···，q}.Moreover，by using a method similar to that of[10，Main Theorem](see also[30])，one may assume that the surfaces Mland points plcan be chosen such that Kl(pl)=，-1≤Kl≤0 on Mlfor all l，and→∞when l→∞.

For a conformal metric Γ on M，we have that

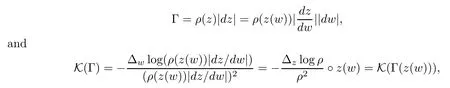
which implies that the Gauss curvature for a conformal metric is independent of the universal cover of M.Thus，we may assume that Mlis simply connected by taking the universal cover of Mlif necessary.Furthermore，by the uniformization theorem，Mlis either conformally equivalent to C or to the unit disc Δ.

For the case where M is the complex plane C，it follows from Lemma 3.1 that Φ(l)is constant map.Thus，Kl≡0 which is a contradiction to the fact that Kl(pl)=.

For another case where M is conformally equivalent to the unit disc Δ，the holomorphic map Φ(l):Δ→P2(C) is ramified over Hjwith a multiplicity of at least mjfor each j.One further knows that if (Pn(C)，D) is hyperbolically imbedded in Pn(C)，then Lemma 3.3 implies that{Φ(l)}is normal;i.e.，there exists a subsequence of holomorphic mapsof{Φ(l)}，still denoted by{Φ(l)}，that converges to a holomorphic map φ uniformly on every compact subset of the unit disc Δ.

If φ is a constant map，then φ maps Δ into a single point Q.Take a hyperplane H not containing the point Q，and let U and V be two disjoint neighborhoods of H and Q，respectively.Then，φ omits a neighborhood of H in P2(C).Since{Φ(l)}converges uniformly on every compact subset of the unit disc Δ，{Φ(l)}omits a neighborhood of H in P2(C) for l large enough.Without loss of generality，we may assume that H:={z2=0}⊂P2(C)，and there exists a positive number ε＞0，such that for all l，≥ε.As discussed in[4，Theorem 1.2]，one gets the following result:

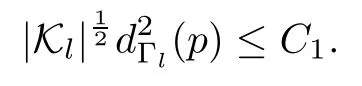
Here C1is a constant，Klis the Gauss curvature of the surface at p，andis the geodesic distance from p to the boundary of M.By using again a method similar to that of[10，Main Theorem]，one gets a contradiction.Thus，φ is not a constant.Since Kl(pl)=for all l，then by Proposition 4.1，there is a subsequence of，say itself，which converges to hjuniformly on every compact subset of the unit disc Δ for each j with 0≤j≤2.Furthermore，h0，h1，h2have no common zeros，so we get a holomorphic map[h0:h1:h2]:M→P2(C).Obviously，φ=[h0:h1:h2].Note that→∞when l→∞，and by Lemma 3.5，the conformal metric ds2:=is complete on the unit disc Δ.Note that Φ(l)are some orbifold morphisms of Δ into (P2(C)，D)，so by Lemma 3.4，φ is also an orbifold morphism of Δ into (P2(C)，D) or φ(Δ)⊂Supp (D).

If φ is ramified over hyperplanes Hjwith multiplicities of at least mjfor all j=1，2，···，q，then Remark 2.2 shows that φ is a constant，a contradiction.Therefore，there exist hyperplanes Hj，j∈J⊂{1，···，q}such that φ(Δ)⊆∩j∈IHj.Furthermore，φ is ramified over hyperplanes Hjwith multiplicities of at least mjfor all j∈{1，2，···，q}J.Assume that φ is k-nondegenerate，obviously，k≤1.Since φ is not a constant，k=1，and there exists only one hyperplane，so we may assume that j0=1 such that φ(Δ)⊆H1.We note that φ can be regarded as an orbifold morphism of Δ into.Furthermore，H2∩H1，···，Hq∩H1are still in general position in H1，since H1，···，Hqare in general position in P2(C).By the assumption that，Lemma 3.1 implies that φ is a constant，which is a contradiction.

In conclusion，(4.2) holds.Thus，there exists a constant C，depending on the set of hyperplanes，but not the surface，such that|K (p)|1/2≤.We have thus completed the proof of Theorem 2.3.

AcknowledgementsWe are grateful to Professor Min Ru for his useful advice and conversation.