CONVERGENCE RESULTS FOR NON-OVERLAPSCHWARZ WAVEFORM RELAXATION ALGORITHMWITH CHANGING TRANSMISSION CONDITIONS*
Minh-Phuong TRAN
Applied Analysis Research Group,Faculty of Mathematics and Statistics,Ton Duc Thang University,Ho Chi Minh city,Vietnam E-mail:tranminhphuong@tdtu.edu.vn
Thanh-Nhan NGUYEN Phuoc-Toan HUYNH
Department of Mathematics,Ho Chi Minh City University of Education,Ho Chi Minh City,Vietnam E-mail:nhannt@hcmue.edu.vn;huynhphuoctoanhcmup@gmail.com
Nhu-Binh LY Minh-Dang NGUYEN Quoc-Anh HO
Faculty of Mathematics and Statistics,Ton Duc Thang University,Ho Chi Minh city,Vietnam E-mail:lynhubinh2211@gmail.com;dang.nm1311@gmail.com;hoquocanh119@gmail.com
Abstract In this paper,we establish a new algorithm to the non-overlapping Schwarz domain decomposition methods with changing transmission conditions for solving one dimensional advection reaction diffusion problem.More precisely,we first describe the new algorithm and prove the convergence results under several natural assumptions on the sequences of parameters which determine the transmission conditions.Then we give a simple method to estimate the new value of parameters in each iteration.The interesting advantage of our method is that one may update the better parameters in each iteration to save the computational cost for optimizing the parameters after many steps.Finally some numerical experiments are performed to show the behavior of the convergence rate for the new method.
Key words domain decomposition method;Schwarz waveform relaxation algorithm;advection reaction diffusion;changing transmission conditions
1 Introduction
Waveform relaxation method (WR) was developed by[17,21]for solving large-scale systems of ordinary differential equations (ODEs).This method has been successfully extended for many classes of problems arising in various practical applications,such as circuit simulations,for example in[28],population dynamics in[13],time-periodic differential algebraic equations in[18],fractional differential equations in[19]and especially for partial differential equations(PDEs) in[15,20].Schwarz waveform relaxation,regarded as a combination of the Schwarz methods (domain decomposition methods) and the waveform relaxation,also has been studied extensively in the last decade throughout their wide applications in physics and engineering (see[25]for the water shallow problem,[4]for the Maxwell’s equations and[29]for the timeperiodic parabolic equations,etc).So far,especial attention has been driven to optimized Schwarz waveform relaxation (OSWR),whose original idea was investigated by many authors in[5,11,14].There has been some outstanding convergence results of this algorithm for linear heat equations in[11,12],for linear wave equations and advection-reaction-diffusion equations in[1,6,8,14,24],for Maxwell’s equations in[3],porous medium models in[16]and so on.One refers to a selection of very recent results in solving boundary value problems of time-dependent problems,such as[10,12]for overlapping method,[1]for overlapping and non-overlapping optimized methods.
Among various parallel domain decomposition techniques,the optimized Schwarz waveform relaxation method is an efficient method,introduced by Gander in[5].This method is well adapted for different time dependent problems and employed to construct numerical schemes with or without overlapping of subdomains.Furthermore,it significantly converges faster than the classical Schwarz method and has the same cost per iteration.It is well known that the convergence rate of this method relies on the transmission condition on the interface between their adjacent subdomains.More precisely,the optimal convergence of this method is obtained by using an approximation of the Dirichlet-to-Neumann operators on subdomains corresponding to the estimated parameters (as this operator is non-local,it can be fairly expensive in the numerical procedure).The idea behind OSWR is finding the best parameter that minimize the convergence rate in the transmission conditions of the problem,with regard to solving the min-max optimization problem.We refer the interested reader to[5,6]for further reading.
Although the optimal transmission parameters found by Gander in[5]enhance the convergence of iterative domain decomposition algorithm and this method is well-posed for advectionreaction-diffusion equations,it was considered very hard to tackle such the optimization problem for some other more complicated problems,especially elliptic problems with highly varying coefficients.To overcome this challenge in case of other types of equations and oversimplify the model,authors in[27]presented a new optimized method to optimize the transmission parameters.More precisely,they introduced a simple algorithm with the minimal problem only instead of solving the min-max problem analytically to obtain the optimal choice of parameter.Experimentally,this scheme of domain decomposition method is efficient,convenient,flexible and robust and also gives good convergence results.Needless to say,this new optimized approach does not give better convergence results than Gander’s method,but it is much simpler,computationally cheap to implement and guarantee the convergence for many other different types of PDEs.
Let us summarize the idea from previous work[27]for computing numerically efficient transmission conditions.Instead of determining parameters pj,qj>0 in each subdomain analytically,ones proposed the technique to approximate these parameters numerically.It is a two-step approach.The first step estimates the initial parameters by minimizing quadrature functions,that are obtained from simplicity of the min-max problem presented in[5].In the second step,one optimized the parameters using the backtracking-Armijo-line search method,which improves the convergence of algorithm.The algorithm yields the good convergence results and confirms the efficiency of this practical approach.We invite the reader to[27,Figures 1 and 2]for more details about these results and experimental comparisons with Gander’s approach.Inspired by this promising approach,the purpose of this paper is to design a new effective algorithm and extend experimental results by approximating optimized parameters for transmission conditions via appropriate sequences.
Before formulating the main result of this paper,let us briefly describe the model problem.We herein focus on a class of one-dimensional advection-reaction-diffusion equations of the type

with the initial data
u (0,·)=u0(·),inΩ,
where the domain Ω=R,the operator L=∂t-+b∂x+c with constants a>0,b,c∈R.This type of advection-reaction-diffusion equation is one of the most famous equations that used to describe models in physics,chemical kinetics,biology and a large class of issues in science and engineering.For the model problem of time dependent equations in one spatial dimension,we study the non-overlapping Schwarz waveform relaxation algorithm,where the domain R is decomposed into two non-overlapping sub-domains Ω1=(-∞,0) and Ω2=(0,+∞).The optimized non-overlapping Schwarz waveform relaxation method consists of solving iteratively two sub-problems on (0,T)×Ω1and (0,T)×Ω2using some coupling transmission conditions at the interface Γ={0}.More precisely,we define bysolution of the following equations

that corresponds to transmission conditions at Γ as

where A1and A2are linear operators,possibly pseudo-differential.We remark that the initial guessesin (1.3) need to be provided later.It is well known that if A1=-∂x+and A2=∂x+,where the operators,for j=1,2,coincide to the Dirichletto-Neumann operators defined as in 2.21,then the Schwarz waveform relaxation algorithm converges in two iterations.However,to our knowledge,due to the non-local operators in time,it may be very expensive to approximate the Dirichlet-to-Neumann operatorsdirectly in sub-problems.To overcome this difficulty,Gander et al.in[1,6]proposed and presented an optimized Schwarz waveform relaxation algorithm.Later,there has been a great deal of work concerning this method developed and attracted attention by many authors via a wide literature,for instance[1,6-9,21,24,25]and references therein.The main idea of the optimized Schwarz waveform relaxation algorithm is to approximate the Dirichlet-to-Neumann operatorsby Sjwhose forms are Sj:=pjIdor Sj:=pjId+qj∂tfor some optimized parameters pj,qj,respectively.The key technique of this method bases on an optimal determination the parameters pj,qjby optimizing the analytic convergence rate of algorithm (1.2)-(1.3) for the advection reaction diffusion equation (1.1).This method is very efficient and accuracte for the class of advection-reaction-diffusion equations.However,for other types of partial differential equations that aside from elliptic and parabolic problems,it can be difficult to solve the corresponding min-max optimization problem.On the other hand,following the numerical approximation scheme presented by Tran&Nguyen in[27],it enables to find the approximation of optimized parameters in transmission conditions.
Our new idea in the present paper is to construct a Schwarz waveform relaxation algorithm with changing transmission conditions corresponding to sequences of parameters in iterative process.Roughly speaking,we solve the numerical problem (1.2)-(1.3) with

The remaining part of this paper is organized as follows.The next Section 2 is devoted to the main results in this paper,in which the mathematical framework of the novel algorithm for OSWR will be presented.In particular,we first state the existence,uniqueness and regularity of the new method and the rest of this section attempts to prove the convergence results for the new algorithm.Moreover,we provide a numerical method to obtain an optimal transmission condition after each iteration.We end up with Section 3 that devoted to present some experimental results to show the convergence results and con firm the robustness and efficiency of our approach.Next,to verify the convergence theory,in this section we also include some numerical experiments and compare the accuracy of various numerical schemes.Finally,some conclusions about the performance of the method and perspectives for further development will be drawn in the last section.
2 A Novel Algorithm:General Results of Well-Posedness and Convergence
This section is devoted to the understanding of well-posedness and the convergence of our main approach throughout the paper.In particular,it enables us to prove the simpler convergence by constructing a sequence of improved parameters in the approximation of Dirichlet-to-Neumann operators on each subdomain.
For studying solutions to our problem,let us now briefly review the function spaces that can be served in theoretical framework:the anisotropic Sobolev spaces.We address the reader to[6,22]for the earlier developments of these function spaces and their properties.
2.1 Function spaces
We first present the standard definition of isotropic Sobolev spaces.Without loss of generality,we use the abbreviation ΩTfor the domain (0,T)×Ω throughout this paper.For a given nonnegative integer s,the Sobolev space Hs(ΩT) is defined by

It can be seen clearly that H0(ΩT)=L2(ΩT) and Hs(ΩT) is the Hilbert space with the following inner product

where〈·,·〉is the usual inner product in L2(ΩT).Moreover,the isotropic Sobolev space Hs(ΩT) is endowed with the norm

where‖·‖denotes the usual norm on the space L2(ΩT).The spaces Hs(ΩT) are said to be isotropic in the sense that they require equal orders of differentiability in each direction.The trace spaces Hs(ΓT) are defined corresponding to the functions on the boundary.
The anisotropic Sobolev spaces are more general than the isotropic ones with two-parameter scale.They were introduced in[22,26]in the requirement of anisotropic Sobolev embedding theorems.For nonnegative integers r,s,one defines
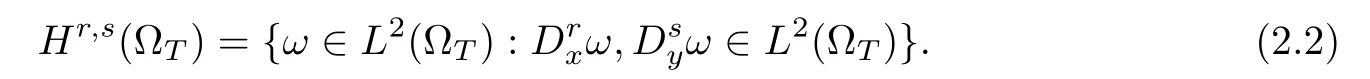
Again,this function space is also a Hilbert space equipped to the following inner product

The norm associated with these anisotropic spaces is given by

One can see that isotropic Sobolev spaces are a special case of the anisotropic ones,when r=s.For further properties of the isotropic and anisotropic Sobolev spaces,we refer the readers to[22,26].
2.2 The algorithm and well-posedness result
For simplicity,in the whole paper we will assume that c≥0,if not we may change variable with=u-βtfor some β+c>0.A function u∈C (0,T;L2(Ω))∩L2(0,T;H1(Ω)) is said to be a weak solution to (1.1) if

for every φ∈H1(Ω).The existence and uniqueness of the weak solution to (2.3) with the initial condition u0∈L2(Ω) and the trace theorem in Hr,scan be found in[22,23].
Let us now describe the numerical algorithm to approximate the weak solution (2.3).For the given initial guess,we study the numerical solutionsto the following equations for each iteration index n∈N as
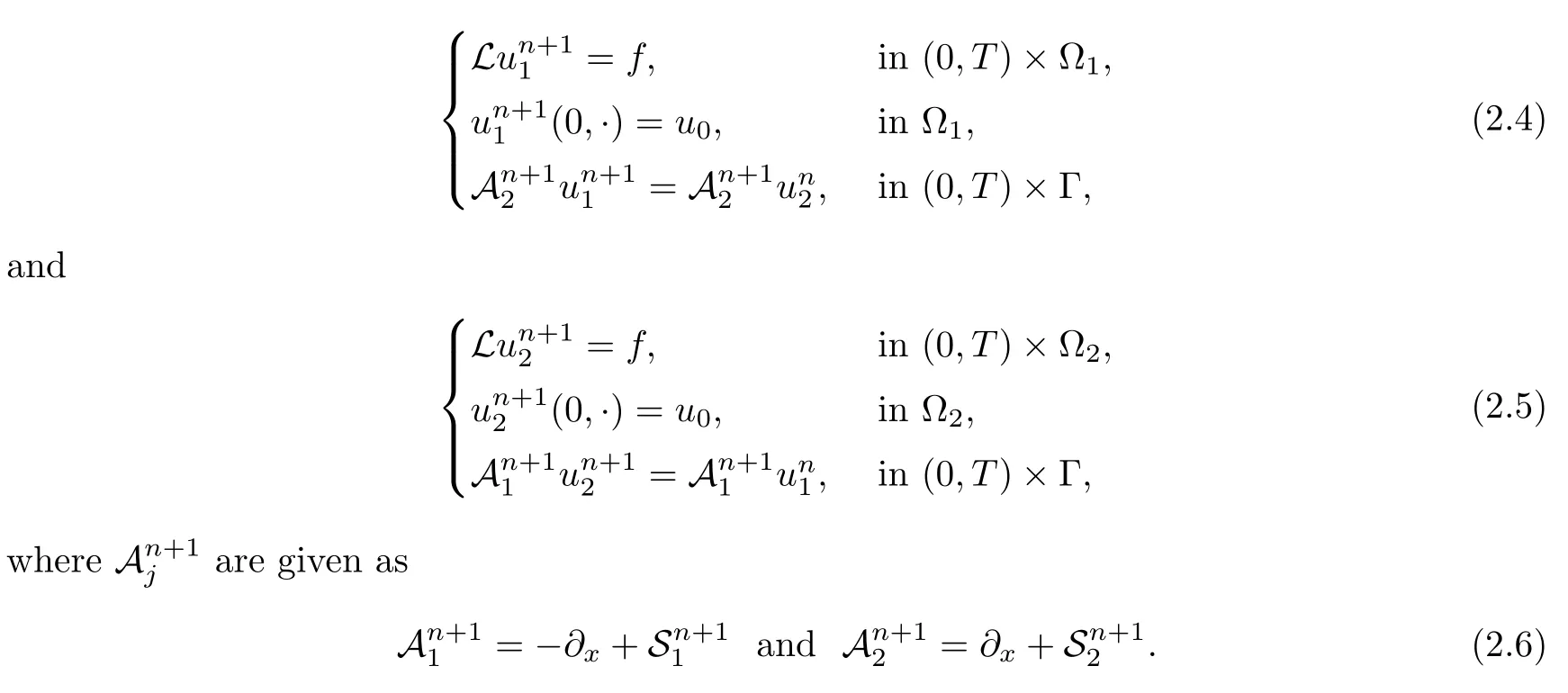
Moreover,we consider the transmission condition in two following cases

The next theorem presents the well-posedness of the new algorithm.The proof of this theorem can be proved by the same method as the proof of[6,Theorem 5.4].
Theorem 2.1Letsuch that

2.3 Convergence results
In the following Theorems 2.2 and 2.3,we establish the convergence theorems for the numerical solutions for the new algorithm defined as in (2.4)-(2.5).Here the transmission conditions (2.6),(2.7) correspond to the sequences of parameterswhich are analyzed instead of one single value of parameters pjor (pj,qj) in each iteration,respectively.
Theorem 2.2Letbe the convergent sequence of real numbers satisfying

ProofLet us define bythe differences between the weak solution u and the numerical solutions of the sub-domain problems (2.4)-(2.5) as follows
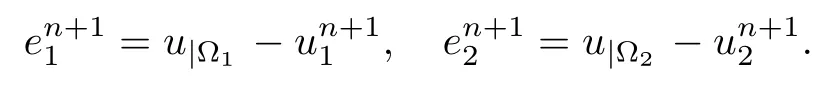
By the linearity of the problems,the errorssatisfy two following homogeneous problems,respectively

Taking the Fourier transform of both sides of the first equation of (2.10) and (2.11),one obtains the corresponding Fourier coefficients ofthat are given by
where θ1,θ2are respectively the roots of characteristic equation
The Fourier transform on the transmission conditions in (2.10) and (2.11) yields that

for all n≥1.Therefore,it deduces from (2.12) that

Our key point of this proof is to show that
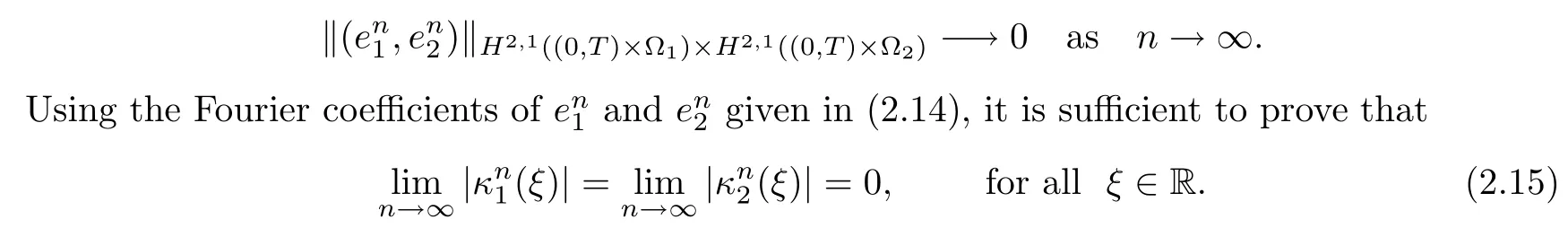
Let us first denote δ=b2+4a (c+iξ),by simple computation one obtains that


which guarantees (2.15) after passing n to infinity.The proof is complete. □

For every ξ∈R,let us present δ as follows

2.4 Methods for parameter determination
In this section,an approach in the determining of the sequence of parameters is proposed.In[5,6],the authors showed that the algorithm (1.2)-(1.3) converges after two steps when the Dirichlet-to-Neumann operators Sjis chosen byfor j=1,2 as

where vjsolves the following problem

for each j=1,2.However,the Dirichlet-to-Neumann operators are non-local in time,so from the computational point of view,it is very expensive to approximate these maps even though many numerical techniques are used.To overcome this difficulty,the authors approximated the optimal transmission operatorsby the new operators corresponding to one parameter p>0 as

or two parameters p,q>0 as
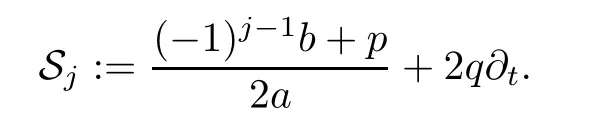
The idea of the optimized Schwarz method is to minimize the convergence rate by choosing the optimized parameters.In other words,one has to solve the following min-max problem:

However,one can see that it is still not easy to solve this optimization problem (2.23).To oversimplify the problem,in this paper,we establish a new algorithm,in which the min-max problem is transformed into a minimization problem only and an additional assumption is required.To be more precise,it means that there exists ψ∈L2(0,T) such that=1 and

For this reason,it enables us to find the parameter by minimizing the following function
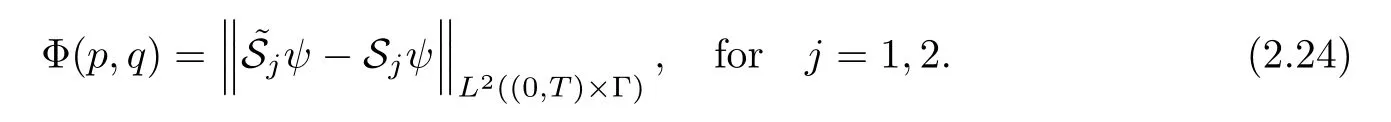
The emphasis of this paper is the changing transmission conditions at every step of the smaller boundary value problems on subdomains instead of studying the problem with a fixed transmission condition as in[5,6,27].In particular,this new approach allows us to approximate(sequences of one single value of parameters) or(sequences of two corresponding parameters) for each iteration step n of the algorithm (2.4)-(2.5).
In Theorems 2.4 and 2.6 below,the sufficient conditions of these sequences will be established which ensure the convergence of our proposed method.


Similar to the above argument from Theorem 2.4,after taking the Fourier transform both sides,one also obtains

where δ=b2+4a (c+iξ).Otherwise,it is easy to compute the partial derivatives ofwith respect to p and q as follows>0 and in a completely similar way as in the proof of Theorem 2.3,we can prove that>0.Therefore,one gets


Thus,we are able to conclude that


The proof is essentially the same as that of Theorem 2.4,it is easy to check thatgiven in (2.34) converges and satisfies (2.9) for some α0>0.Thanks to the assumption (2.25) for some s>,there holds

Hence,the right hand side of (2.36) is integrable andconverges pointwise to.Applying Lebesgue’s dominated convergence theorem once again,one gets that

Analogously,together with the following elementary estimate

one also proves that
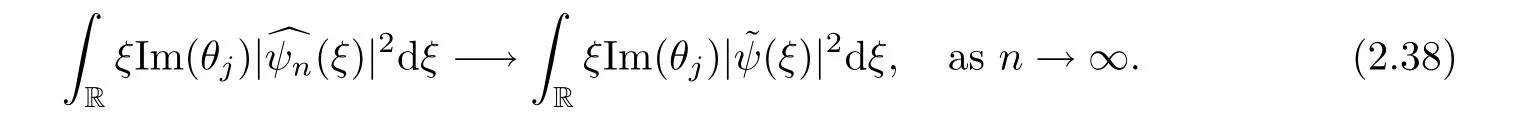
Finally,combining all estimates in (2.35),(2.37) and (2.38),it follows that the sequenceconverges to a positive number.Theorem 2.6 is completely proved. □
Let us end up this section with two algorithms devoted to present the ideas proposed in this paper,that leading to one and two sequences of parameters satisfying conditions in Theorems 2.2,2.3,2.4 and 2.6,respectively.One can say that these algorithms take advantages from OSWR method and the changing transmission conditions through iterations in our method.

3 Experimental Results
With algorithms presented in the preceding section in hand,we are in position to illustrate the convergence results with numerical experiments.This section includes numerical technique for the solutions of two examples in one dimension:on advection-reaction-diffusion with constant coefficients (ARD) and convection-dominated diffusion (CDD) equations.We also present here some comparisons between implementations based on our algorithms and the OSWR method.
3.1 Advection-reaction-diffusion problems
In this section,in order to observe the robustness of our proposed algorithms,and to verify whether it converges well or not,we first perform several numerical tests for an example of advection-reaction-diffusion equations (ARDs) in one-dimension as follows

with Dirichlet boundary condition
u (t,-3)=u (t,3)=0,in (0,T),
and the initial condition

where the domain Ω=(-3,3) and our results are performed in the time interval (0,1).
To solve the problem (3.1) by Schwarz waveform relaxation method without overlapping,one divides the domain Ω into two subdomains of equal size Ω1=(-3,0) and Ω2=(0,3).And for the discretization of each sub-problem,we employ the P1finite element method with spatial step Δx=0.01 and the implicit Euler scheme in time with the time step is chosen small enough Δt=0.01.
Here,we are interested in specifying the relative error (in L2norm) between the solution obtained with our above described algorithm and the approximate solution obtained after the P1finite element method,so-called the reference solution and denoted by ur.Such the relative error will be defined by err=.It is worth mentioning that the reference solution here is obtained by finite element method with very small spatial step Δx=10-4and time step Δt=10-4.
3.1.1 The first case:
This section is concerned with algorithm with one sequence of parameters as described in previous section.We first consider some numerical results when the operator Sjin transmission conditions are characterized by a sequence of one-single value of parameterat every iteration step n.Herein,we will study the influence of the sequences of parametersin the transmission condition to the convergence results.To verify theoretical convergence results proved in Theorems 2.2 and 2.4 when,we analyze the algorithms for several test cases.
For the first test,when the chosen sequence of parameters is not convergent but satisfies (2.9)(as stated in Theorem 2.2),we address the reader to Figures 1 and 2.More precisely,in this figure,for each j=1,2,two randomly non-convergent sequences ofare tested to illustrate the assertion of Theorem 2.2.And as we will see,Figures 1(b) and 2(b) show that the algorithm fails in the randomly non-convergent case,leading to the oscillation of relative errors.
For the second test case,when the sequence of parameters is convergent,but chosen randomly and satisfies (2.9)(as stated in Theorem 2.2),results shown in Figure 3.It can be seen that the convergent condition of sequenceis important to assure the error convergence to zero in our results.
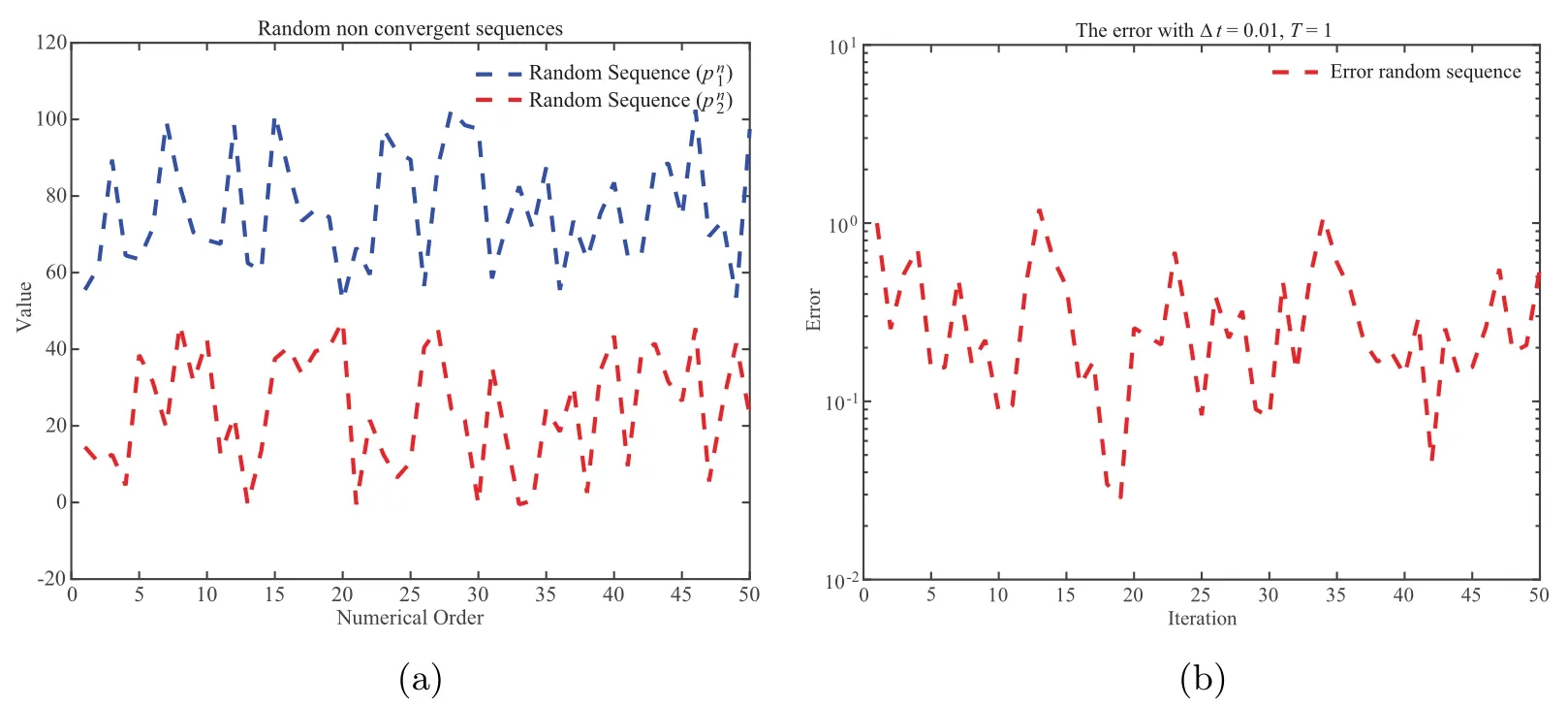
Figure 1 Results with randomly non-convergent sequences of .
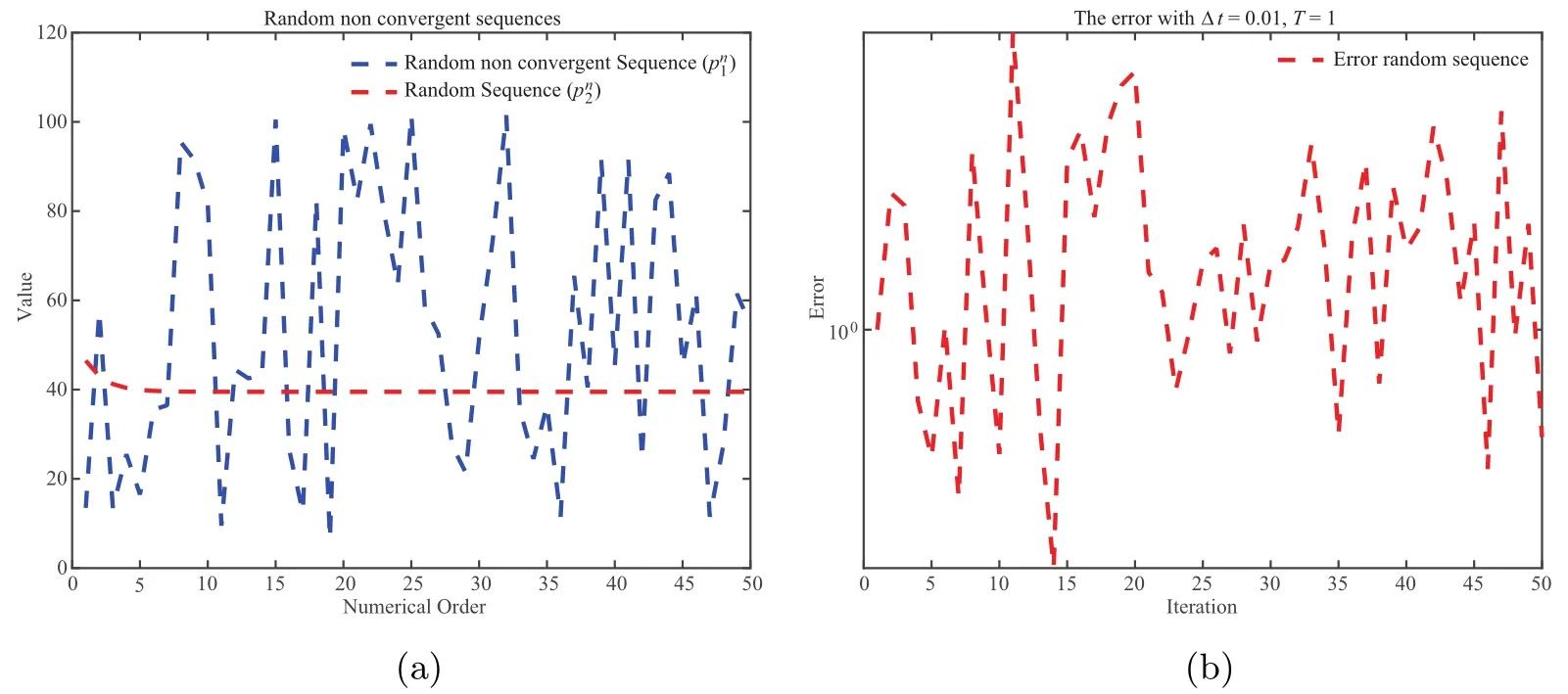
Figure 2 Results with randomly sequences of .

Figure 3 Results with the convergent random sequence of parameters .
In Figure 4,we perform the test with choosing three convergent random sequences or parameters.This test shows that the convergence rate depends on the sequences of parameters.It is worth mentioning that Theorems 2.4 and 2.6 play a key role to choose sequences of parameters to obtain a good behavior of convergence rate.Hence we turn to the last test case when the chosen sequence of parameters follows conditions in Theorem 2.4,it is clear that Figure 5(b) possibly resulting in a convergence pattern.Figures 3,4 and 5 show how the choice of corresponding sequences (presented in Theorem 2.4) affects the convergence of our method.Figure 5 illustrates the efficiency and the performance of our algorithm as stated and proved in Theorems 2.2 and 2.4,respectively.As a consequence,it yields better results than that of the second test case.It can be seen that with the new framework,we can get the rigorous and simple convergence proofs.

Figure 4 Errors when choosing three convergent random sequences of parameters

Figure 5 Results with the choice of convergent determined sequence of parameters ,follows Theorem 2.4.
3.1.2 The second case:
The second one aims to test convergence rate for the case when operator Sjin transmission conditions are replaced by a sequencechanging corresponds to iteration number via index.And it is characterized by the indicated sequence of two valuessuch that.We illustrate our results in Figure 6 firstly for the randomly non-convergent sequences similar to the previous section,respectively.Figure 6 allows us to conclude that the convergence result will be fail without convergent assumption on the sequence of parameters.
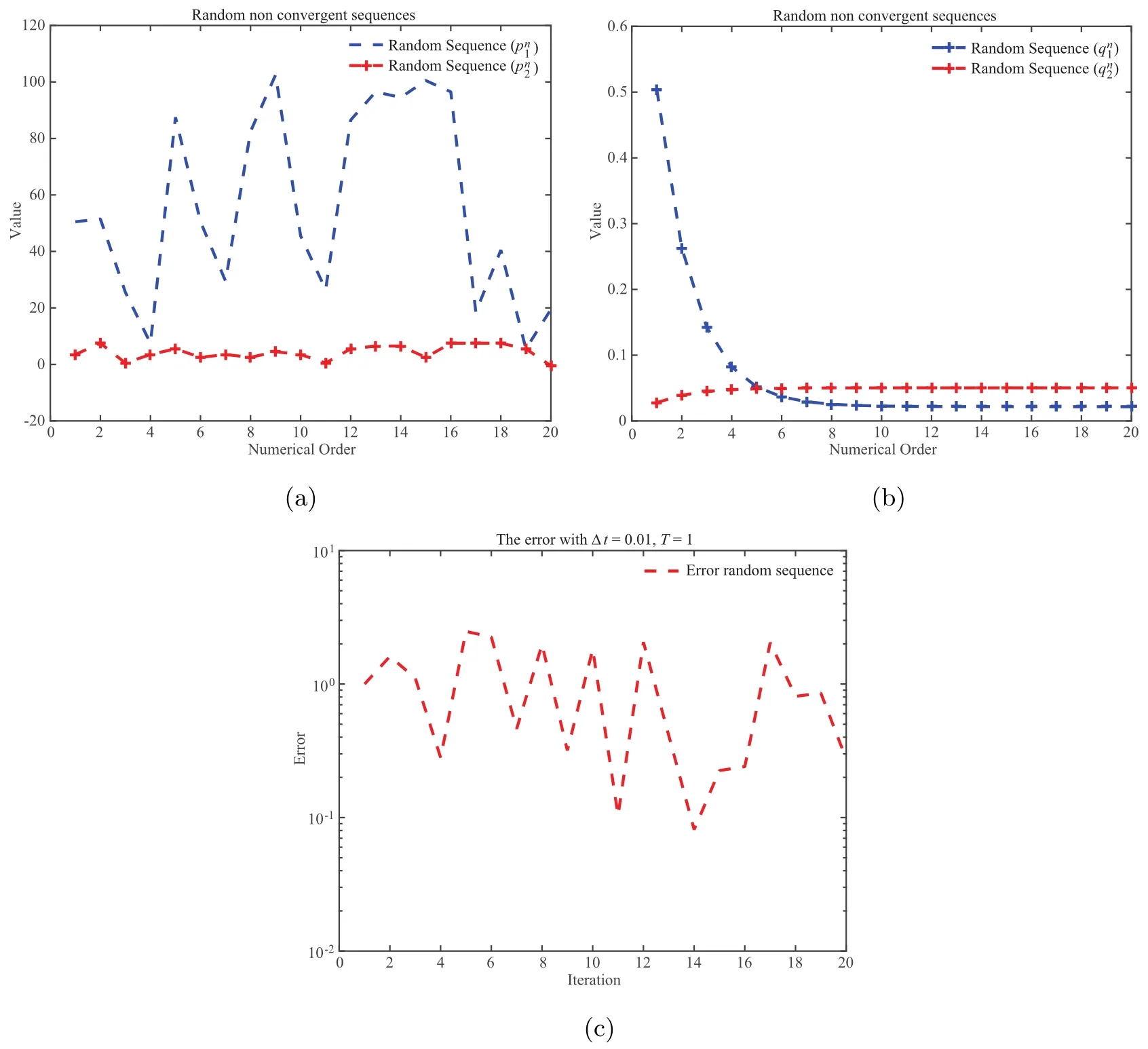
Figure 6 Results with randomly non-convergent sequences of .
In the next test,we present the errors with several randomly convergent sequences of parameters which have not been shown for simplicity.It is clear from Figure 7 that with our technique,it exhibits a good rate of convergence,even when choosing three randomly convergent sequences of parameters.Finally,results obtained are shown in Figure 8 gives us a better determination of parameters provided as in Theorem 2.6.

Figure 7 Errors when choosing three randomly convergent sequences of parameters
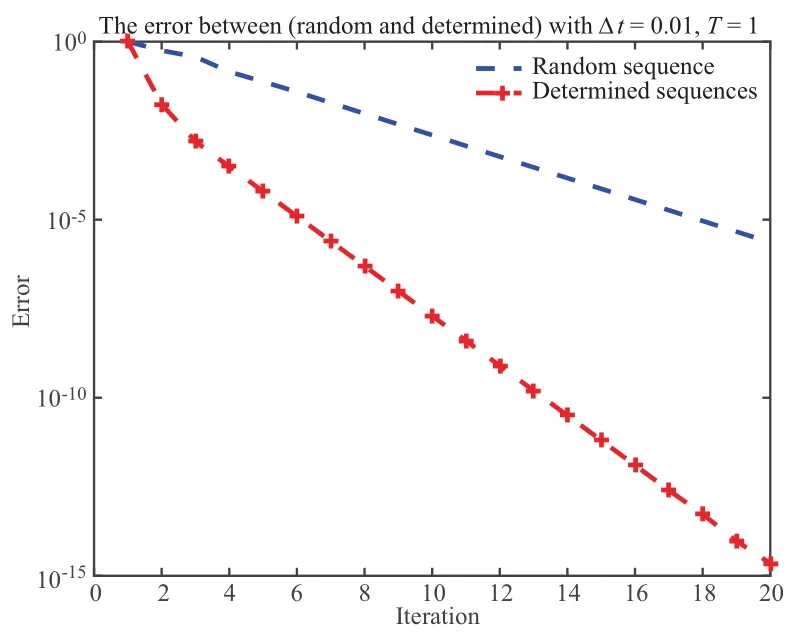
Figure 8 Errors when choosing a convergent determined sequence of parameters ,follows Theorem 2.6
3.1.3 Convergence comparisons with OSWR method
This section is devoted to investigating some comparisons with the OSWR method,that was developed in a series of remarkable papers by M.Gander and his collaborators[5-8],etc.
For the sake of comparison,the solution of (ARD) equation obtained by applying OSWR method in[5]together with the proposed algorithms of one/two sequences of parameters are also carried out,respectively.We have tested the methods for a number of iterations N=20 to compare the relative errors,and convergence results are graphically summarized in Figure 9.With our technique,the sequences of parametersandare accordingly adjusted following Theorems 2.2,2.4 and Theorems 2.3,2.6.
In Figures 9,one observes that the rate of convergence of our method is comparable to OSWR method.Numerical results reveal that the present method converges within a few iterations.In general,our method enjoys good rates of convergence.However,compare to OSWR algorithm when using the same input arguments in (3.1),the convergence rate is slower than OSWR algorithm.Actually,we could not expect our algorithm to have a better convergence then OSWR algorithm,as aforementioned,simply because in our algorithms,there is no presence of the min-max optimization problem (2.23).The issue of solving this optimized problem can be quite a challenge,especially with other types of partial differential equations that commonly arise in mathematical physics.Due to the difficulty related to optimization problems,it emphasizes that our algorithms are less complicated,more efficient than the OSWR technique,and well-suited for a large class of PDEs.

Figure 9 Comparison to OSWR method.
3.2 Convection-dominated diffusion problems
In this part,our approach will be considered to test with the convection-dominated diffusion problems (CDD) of the type
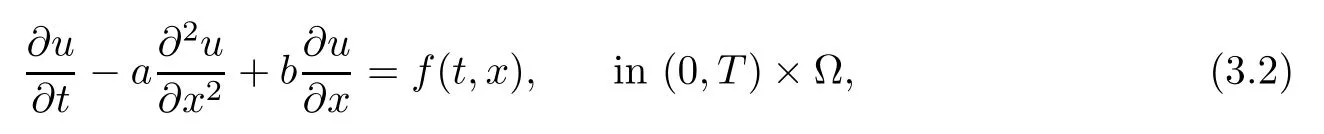
where b≫a>0.Here,we work on the domain Ω=(-3,3),f (t,x)=exp (-t) sin (πx) and the time interval length T=1.The given boundary and initial conditions are the same as problem (3.1).It is worth convincing the readers that the efficient numerical convergence is also needed in practice.Regarding to the example in (3.1),we choose a=0.2 and b=10;20;30,respectively to demonstrate the applicability of our approach.
In Figure 10,numerical experiments indicate that the convergencerate is also fast.However,compare to what obtained with ARD problem in Section 3.1,it can be seen that results on ARD problem achieving higher convergence rates than the CDD one.Moreover,as seen in Figure 10,the rate of convergence depends on the value of b.Different values of b give us different rates of convergence,the smaller values of b leads to the faster convergence.

Figure 10 Convection-dominated problems with determined sequence of parameters ,follows Theorem 2.6.
4 Conclusion
In this paper,the new algorithm for OSWR method in the problem of advection-reactiondiffusion is considered,in which we proposed the construction of sequence of parameters to approximate Dirichlet-to-Neumann operators in transmission conditions changing through each iteration.Using a sequence instead of specifying an optimal parameter as in[5]or parameter estimation via two steps as in[27],we provide a simple approach to perform numerical results for Schwarz waveform relaxation method and is guaranteed to be convergent.Here,the theoretical study of such approach has been carried out,including the study of the well-posedness and the general sufficient conditions for the convergence.
To illustrate the theoretical results,some examples are investigated to verify convergence results and to illustrate the efficiency of our proposed method.In particular,some numerical experiments has been formulated that showed the convergence with the sequence of parameters described in our main theorems.There are two types of transmission conditions in this survey,the sequence of one-single value of parametersand another is characterized by two parameters.Experiments show that the proposed algorithm is convergent.
Furthermore,we also include some convergence comparisons between ours and the effective OSWR method presented by M.Gander et al.Although we cannot hope to obtain a better convergence rate than OSWR method,our approach is cheap,easy and generally applicable to a large class of PDEs.It is worth to be noted that in this paper,we prefer to emphasize the two important advantages of the algorithm:the first one is the is computational efficiency,easier and cheaper to implement via the elimination of min-max problem;the second advantage is that it can be applied not only for advection-reaction-diffusion problems but also for different classes of partial differential equations,especially for the elliptic problems with highly varying coefficients.
Although in the present paper,the algorithm and convergenceresults are only presented and illustrated in the two-subdomain case for one-dimensional problems,we believe that this simple technique can be extensively applied to any linear/nonlinear problems of partial differential equations,in multi-dimensional cases,or with non-smooth domains,etc and our algorithms can be performed numerically into any number of sub-domains for the purpose of parallel computation.For further research,we are going to improve the results by determining the optimal the sequences of parameters numerically (where the min-max optimized problem is still eliminated).This work will be detailed in our forthcoming paper,and furthermore,inspired by the recent work[2],the two-dimensional problems are also presented.
 Acta Mathematica Scientia(English Series)2022年1期
Acta Mathematica Scientia(English Series)2022年1期
- Acta Mathematica Scientia(English Series)的其它文章
- UNDERSTANDING SCHUBERT’S BOOK (II)*
- MOMENTS AND LARGE DEVIATIONS FOR SUPERCRITICAL BRANCHING PROCESSES WITH IMMIGRATION IN RANDOM ENVIRONMENTS*
- FURTHER EXTENSIONS OF SOME TRUNCATED HECKE TYPE IDENTITIES*
- ASYMPTOTIC GROWTH BOUNDS FOR THE VLASOV-POISSON SYSTEM WITH RADIATION DAMPING*
- RIEMANN-HILBERT PROBLEMS AND SOLITONSOLUTIONS OF NONLOCAL REVERSE-TIME NLS HIERARCHIES*
- THEORETICAL AND NUMERICAL STUDY OF THE BLOW UP IN A NONLINEAR VISCOELASTIC PROBLEM WITH VARIABLE-EXPONENT AND ARBITRARY POSITIVE ENERGY*
