THEORETICAL AND NUMERICAL STUDY OF THE BLOW UP IN A NONLINEAR VISCOELASTIC PROBLEM WITH VARIABLE-EXPONENT AND ARBITRARY POSITIVE ENERGY*

Ala A.TALAHMEH

Department of Mathematics，Birzeit University，West Bank，Palestine E-mail:atalahmeh@birzeit.edu

Salim A.MESSAOUDI†

Department of Mathematics，University of Sharjah，P.O.Box 27272，Sharjah，UAE E-mail:smessaoudi@sharjah.ac.ae

Mohamed ALAHYANE

Department of Mathematics，RISE，University of Sharjah，P.O.Box 27272，Sharjah，UAE E-mail:malahyane@sharjah.ac.ae

Abstract In this paper，we consider the following nonlinear viscoelastic wave equation with variable exponents: where μ is a nonnegative constant and the exponent of nonlinearity p (·) and g are given functions.Under arbitrary positive initial energy and specific conditions on the relaxation function g，we prove a finite-time blow-up result.We also give some numerical applications to illustrate our theoretical results.

Key words nonlinear damping，blow up，fi nite time，variable nonlinearity，arbitrary positive energy

1 Introduction

In this work，we consider the following nonlinear viscoelastic problem with variable exponents:

where Ω is a bounded domain，T＞0，μ≥0，p (·) is a variable exponent and g is a C1nonnegative and nonincreasing function satisfying some additional conditions to be specified later.These problems appear in many modern physical and engineering models such as electrorheological fluids (smart fluids)，fl uids with temperature-dependent viscosity，nonlinear viscoelasticity，filtration processes through a porous media and image processing.More applications and details on the subject can be found in[3，4，13].

In the absence of the viscoelastic term (g≡0)，problem (1.1) has been discussed by many authors and several results concerning existence，stability and blow up have been established.See in this case，[1-3，7，8，14-19].In the presence of the viscoelastic effect (g0)，Gao and Gao[6]considered the following nonlinear equation

and established the existence of weak solutions.Ferreira and Messaoudi[5]studied a nonlinear viscoelastic plate equation，with a nonstandard lower order perturbation，of the form

They proved a general decay result for appropriate conditions on g，f and the variable exponent operator.Recently，Park and Kang[22]considered the equation

and established a blow-up result for certain solutions with positive and non-positive initial energy.Their work generalized many others works in the literature，but with constant exponents.In this work，we prove a blow up result for certain solutions with arbitrary positive initial energy.Precisely，we intend to push the result of Kafini and Messaoudi[11]，which has been established for (1.1) but with p constant，to our present problem.

The equation in (1.1) can be considered as a model for the propagation of nonlinear waves in a viscoelastic material in the presence of a non-standard source term caused by the“smart”nature of the medium.To the best of our knowledge，there is no work that treated this problem.This work is organized as follows.In Section 2，we recall the definitions of the variable exponent Lebesgue spaces，Lp (·)(Ω)，the Sobolev spaces，W1，p (·)(Ω)，as well as some of their properties.We also state，without proof，an existence result and a proposition to be used in the proof of our main result.In Section 3，we state and prove our main result and show how to construct initial data satisfying our conditions of blow up.In Section 4，we present two numerical examples to illustrate our theoretical findings.

2 Preliminaries

In this section，we present some preliminaries about the Lebesgue and Sobolev spaces with variable exponents (see[3，13]).Let Ω be a domain of Rnwith n≥1 and p:Ω→[1，∞]be a measurable function.The Lebesgue space Lp (·)(Ω) with a variable exponent p (·) is defined by

Lp (·)(Ω)=｛v:Ω-→R;measurable in Ω and ρp (·)(v)＜+∞｝，

where ρp (.)(v)=RΩ|λv (x)|p (x)dx is a modular.Equipped with the following Luxembourg-type norm

Lp (·)(Ω) is a Banach space (see[13]).The variable-exponent Lebesgue Sobolev space W1，p (·)(Ω) is defined as follows

This space is a Banach space with respect to the norm

Definition 2.1A variable exponent is said to satisfy the log-Hölder continuity condition，if for some A＞0 and for any 0＜δ＜1，we have

We also set

Lemma 2.2([13]) If p:Ω→[1，∞) is a measurable function with p2＜∞，thenis dense in Lp (·)(Ω).

Lemma 2.3([13]) If p:Ω→[1，∞) is a measurable function with p2＜∞，then，for any v∈Lp (·)(Ω)，

Corollary 2.4If 1≤p1≤p (x)≤p2＜+∞holds，then

Lemma 2.5(Poincaré’s inequality[13]) Let Ω be a bounded domain of Rnand p (·) satisfies (2.1) such that 1≤p1≤p (x)≤p2＜+∞，then there exists a positive constant C depending only on p1，p2and Ω such that

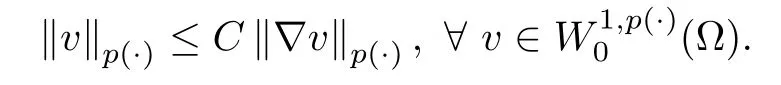
Lemma 2.6(Embedding[13]) Let Ω be a bounded domain of Rn，with a smooth boundary and p (·) be an exponent satisfying 1≤p1≤p (x)≤p2＜+∞.If p (·)，q (·)∈such that q (x)≤p*(x)，where

Then，the embedding W1，p (·)(Ω)Lq (·)is continuous.Moreover，if q (x)＜p*(x)，then the embedding is continuous and compact.

In particular，we have

Lemma 2.7([13]) If p:→[1，∞) is a continuous function and

Lemma 2.8(Hölder’s Inequality[13]) Let p，q≥1 be measurable functions defined on Ω such that

If f∈Lp (·)(Ω) and g∈Lq (·)(Ω)，then fg∈L1(Ω) and

‖fg‖1≤2‖f‖p (·)‖g‖q (·).

Proposition 2.9([12]) Assume that Φ∈C2([0，T)) satisfying

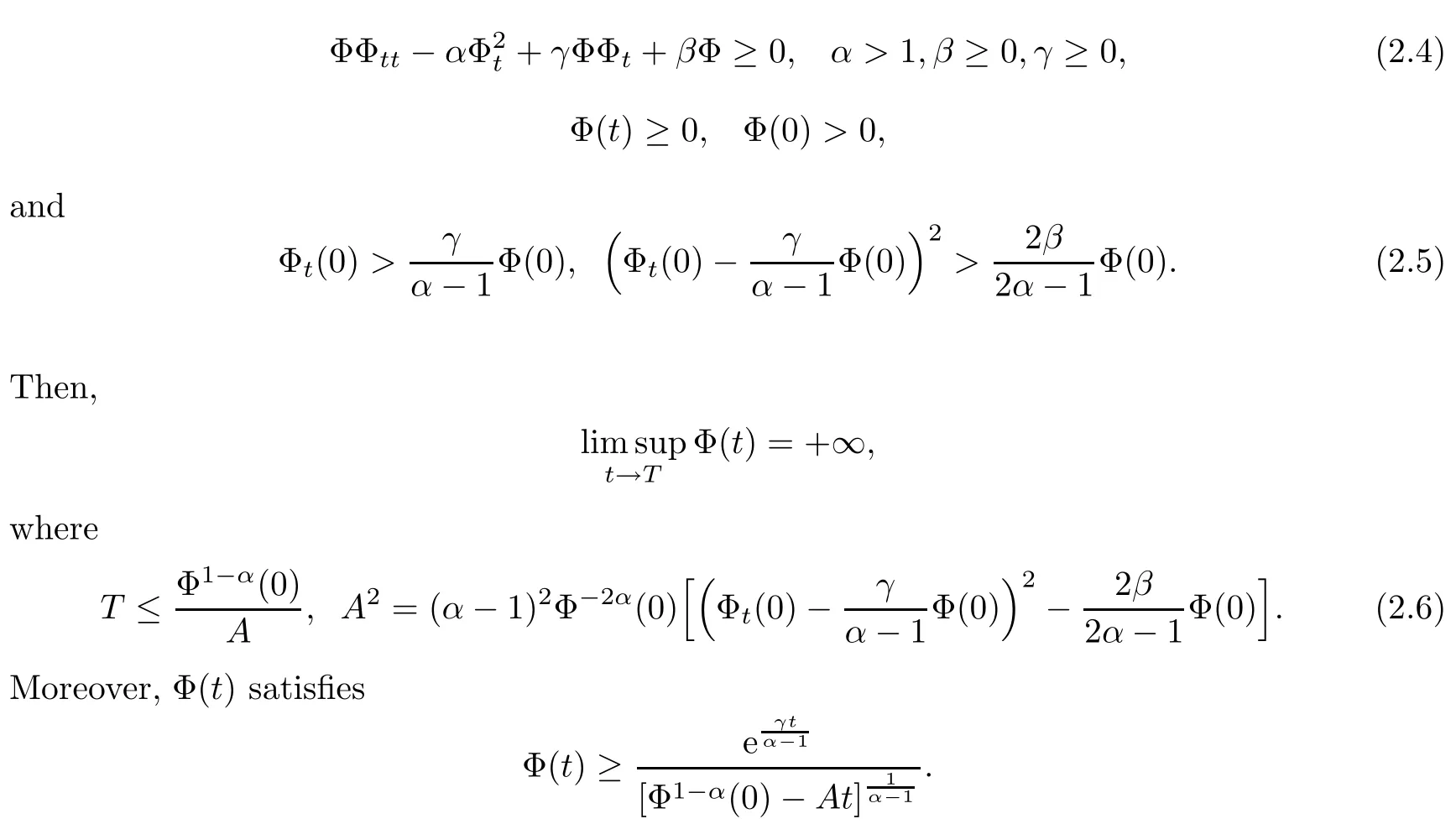
For the relaxation function g，we assume that

(H) g:[0，+∞)→(0，+∞) is a differentiable function such that

Theorem 2.10(Existence Theorem) Assume that (H) holds and p (·)∈satisfies (2.3).Then for any initial data

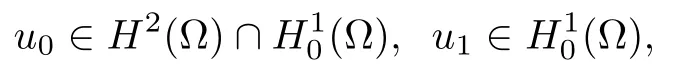
problem (1.1) has a strong solution

for some T＞0.

The proof of this theorem goes exactly like that of the existence result in[6，17].

3 Blow-up

In this section we state and prove our main blow-up result.For this purpose，we define the energy of the solution by

Theorem 3.1Assume that (H) holds and p (·)∈satisfies (2.3).Assume，further，that p1＞2 and

If the initial data are such that

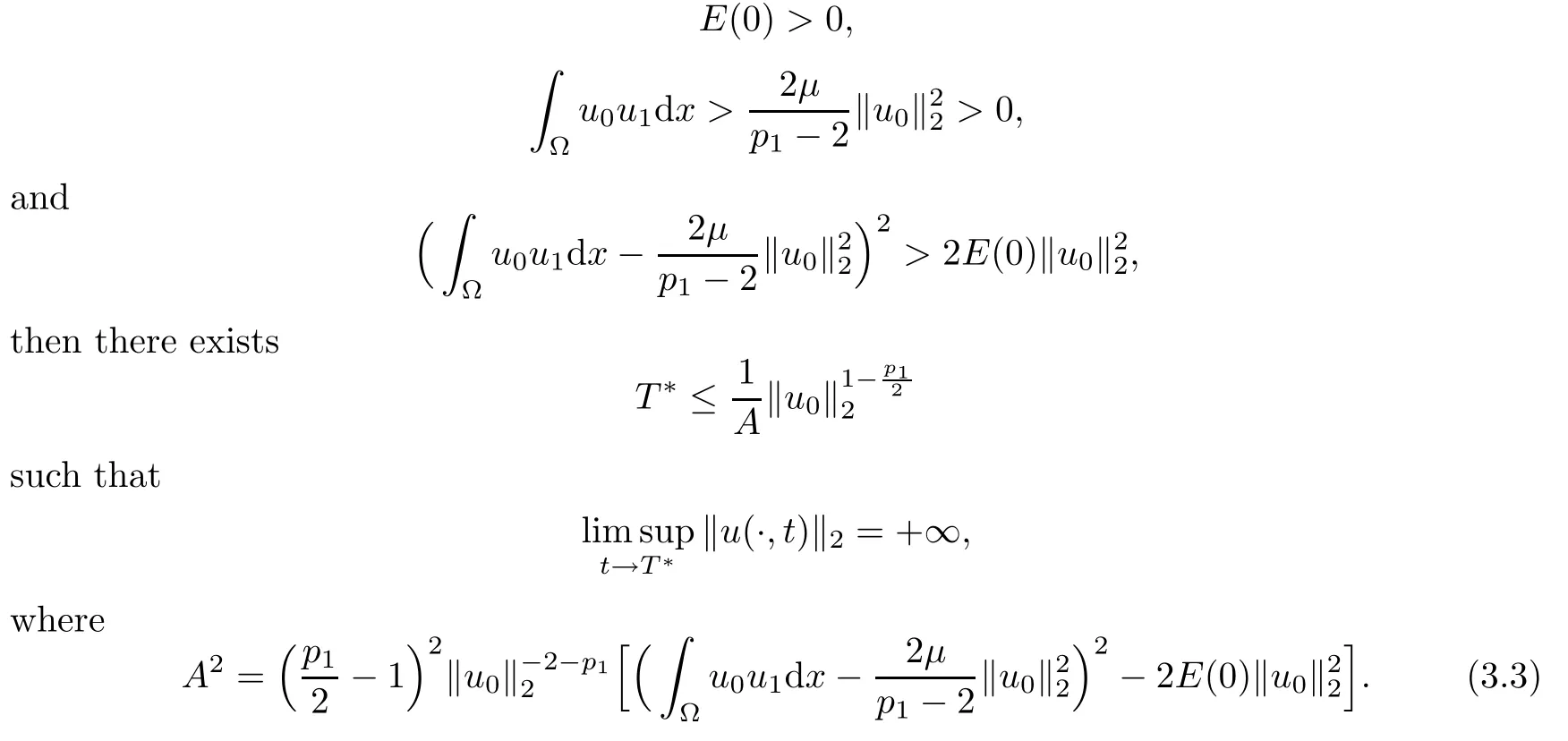
ProofWe multiply (1.1) by u and integrate over Ω to get

The third term in (3.4) is estimated as follows

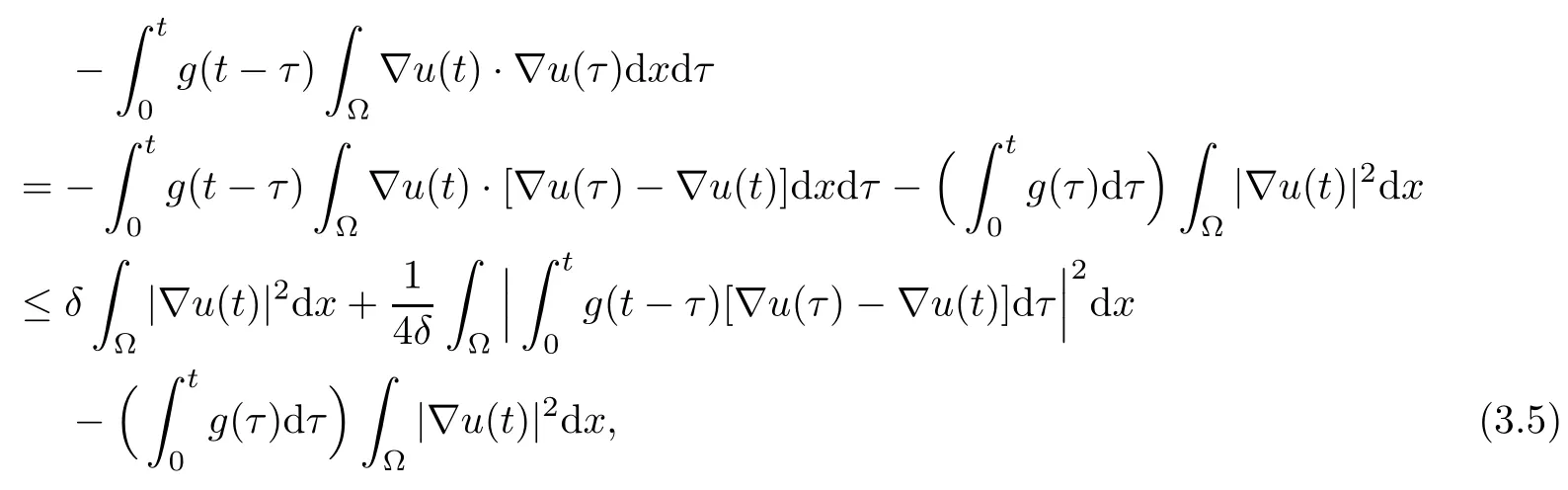
where δ＞0.

Using Cauchy-Schwartz’inequality，we have (see[11，22])

Thus，(3.5) becomes

and，consequently，(3.4) takes the form

Similarly，we multiply (1.1) by utand integrate over Ω to get

It is well known，see[20]，that

Therefore，(3.8) becomes

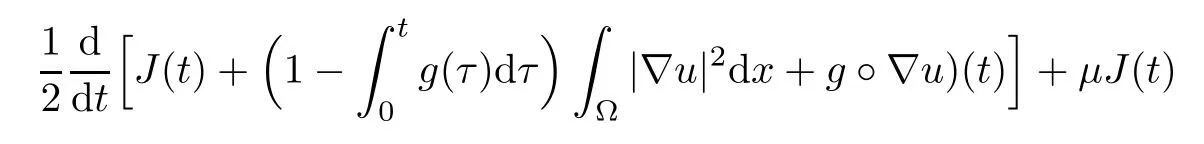
Integration of (3.9) over (0，t)，dropping

Combining (3.7) and (3.10)，we arrive at

At this point，we choose δ＞0 such that

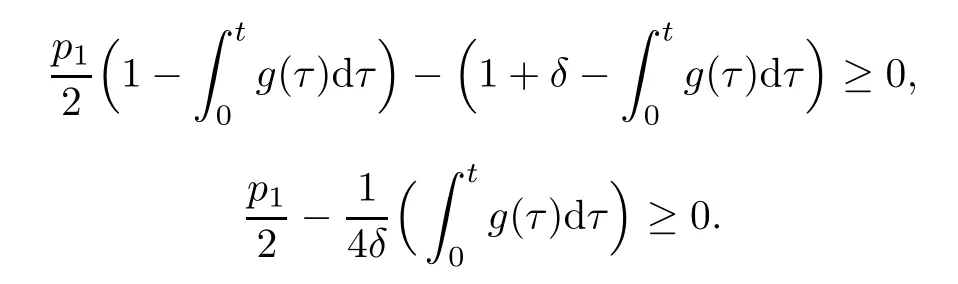
This is，of course，possible because of (3.2).Thus，(3.11) yields the following differential inequality

Again using Cauchy-Schwarz’inequality，we easily deduce

Combining the last two inequalities，we obtain

Now，comparing (3.12) with (2.4)，we easily see that

Thus，by Proposition 2.9，there exists

where A is given by (3.3).Moreover，we have

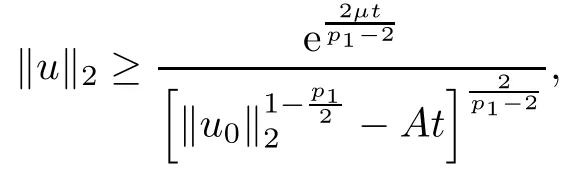
which is the desired result. □

Remark 3.2This result extends the one in[11]to problems with variable-exponent nonlinearities.

Remark 3.3Conditions assumed in Theorem 3.1 are compatible for μ≥0 small enough.To show this，we fix u0∈large enough so that

and λ large enough (if needed)，so that

Now，using (3.16)，we have

Comparing (3.17) and (3.18)，it remains to show that

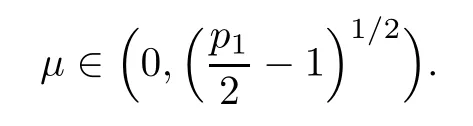
For μ=0，it enough to take λ large.It is clear that the smaller μ is the larger“positive”initial energy can be taken.Moreover，this gives an indication that larger dampings may prevent solutions with positive energy from blowing-up.

4 Numerical Results

In this section，we present an application to illustrate numerically the blowup result of Theorem 3.1.To do this，we exploit a numerical scheme based on finite element method in space to solve problem (1.1)，for n=1，2.Letting V=，multiplying (1.1)1for a given t by v∈V，integrating over Ω and using the Green’s formula，we get the variational formulation of (1.1)，such that

where f (t)=|u (t)|p (x)-2u (t) and a dot represents a time derivative.

For the discretization，we use a Galerkin finite element method to approximate the solution of the problem (4.1).Let

where each Ki=is an element of the triangulation，E is the reference simplex andis an invertible affine map.The associated finite element space given by

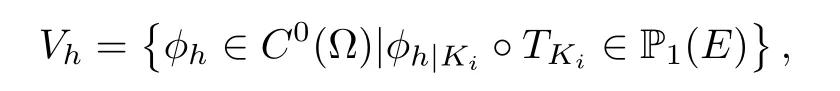
where P1(E) is the space of polynomials of degree at most one on E.Replacing V by the finite-dimensional subspace Vh，we get the following semi-discrete form of (4.1)，

where Πhdenotes the L2-projection from L2(0，1) onto Vh.By usingthe nodal basis of Vh，the approximate solution uh(t) takes the following form

with the time-dependent coefficients ξi(t)∈R.

Next，let tn=nΔt be a partition of the interval (0，T) where n=0，1，···，Ntand

Δt=T/Nt.

Using (4.3) and taking v=φj，j=1，···，Nhin (4.2)，the approximation solution

satisfies the following matrix form

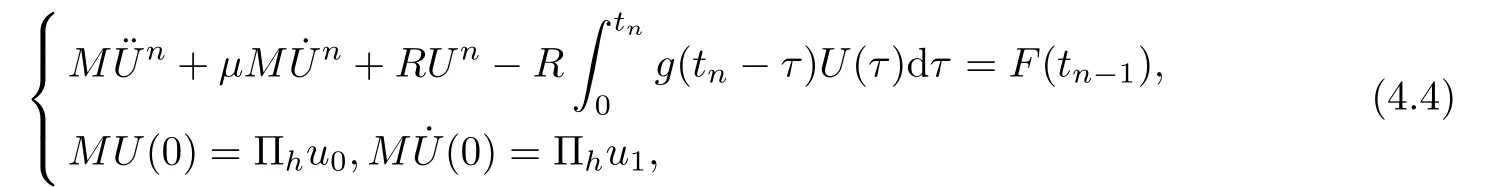
where M，R are the mass and the stiffness matrices，respectively，corresponding to the shape functions，see[9，10].Next，to solve the system (4.4)，we use a Newmark method[21，24].

4.1 One-dimensional problem

We consider the one-dimensional case of the problem (1.1) subject to the following choices Ω=(0，1)，p (x)=2+，g (t)=exp (-2t)，μ=1/40 and initial conditions:

Then using the previous scheme，the spatial interval (0，1) is subdivided into 500 subintervals，where the spatial step h=0.002 and the time step Δt=0.01.We run our Matlab code in time till our solution reaches the blow-up.

The obtained results are shown in Figure 1，where we present the approximate solution Unfrom iteration n=1(t=0) to the final iteration n=9(t=0.08) at which the blowup occurs.

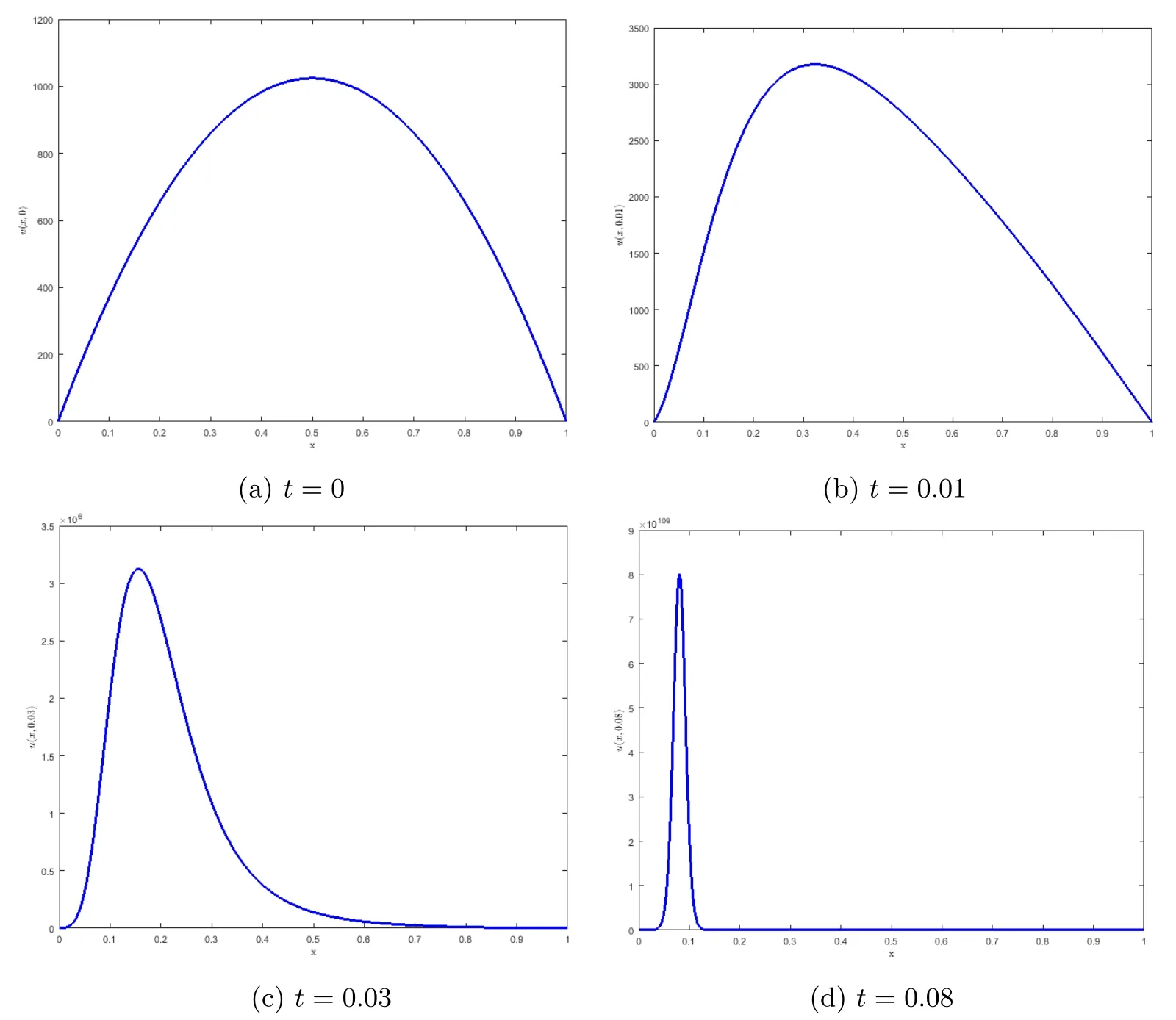
Figure 1 One-dimensional numerical results of Un at different times

In Figure 2，we plot the numerical values of‖Un‖2according to time iterations.We observed that the curve blows up from the time t=0.08，which is compatible with the results proved in Theorem 3.1 for T*＞0.08.

Figure 2 ‖Un(t)‖2

4.2 Two-dimensional problem

We consider the two-dimensional case of the problem (1.1)，subject to the following choices Ω=｛(x，y)/x2+y2＜1｝，p (x，y)=2+，g (t)=exp (-2t)，μ=1/40 and initial conditions:

Then using the previous scheme，where the triangulation Ωhconsists of 281 triangles with 162 degrees of freedoms，we construct a mesh generator in MATLAB[23]，see the mesh-grid in Figure 3.We run our 2D code with a time step Δt=0.01，which is small enough to catch the below up behavior.

Figure 3 Uniform mesh grid of Ω

In Figure 4，we show the approximate numerical results of the solution Unat different time iterations n=1(t=0)，n=2(t=0.01)，n=6(t=0.05) and n=9(t=0.08)，where the blowup is occurring at instant t=0.08.The left column of Figure 4 shows the approximate solutions in a 3D presentation and the right column shows their projections on 2D to have a view from above with a color barre indicating the values.

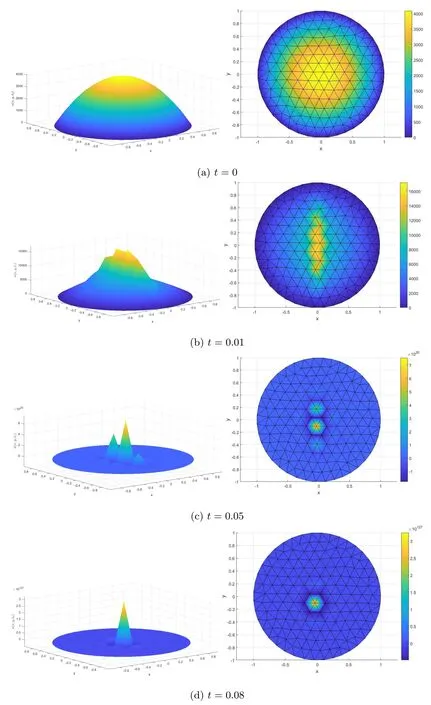
Figure 4 Two-dimensional numerical results of Un at different times

Figure 5 presents the numerical values of‖Un‖2during the time iterations.It shows that the blowup of the solution takes place at t=0.08 as their magnitude orders drastically jumped high.Again our numerical results for 2D case are compatible with the theoretical results proved above.

Figure 5 ‖Un(t)‖2

AcknowledgementsThe authors thank Birzeit University and Sharjah University for their support.The second and the third authors are sponsored by MASEP Research Group in the Research Institute of Sciences and Engineering at University of Sharjah.Grant No.2002144089，2019-2020.