RIEMANN-HILBERT PROBLEMS AND SOLITONSOLUTIONS OF NONLOCAL REVERSE-TIME NLS HIERARCHIES*

Wenxiu MA (马文秀)

Department of Mathematics，Zhejiang Normal University，Jinhua 321004，China

Department of Mathematics，King Abdulaziz University，Jeddah 21589，Saudi Arabia

Department of Mathematics and Statistics，University of South Florida，Tampa，FL 33620-5700，USA School of Mathematical and Statistical Sciences，North-West University，Mafikeng Campus，Private Bag X2046，Mmabatho 2735，South Africa E-mail:mawx@cas.usf.edu

Abstract The paper aims at establishing Riemann-Hilbert problems and presenting soliton solutions for nonlocal reverse-time nonlinear Schrödinger (NLS) hierarchies associated with higher-order matrix spectral problems.The Sokhotski-Plemelj formula is used to transform the Riemann-Hilbert problems into Gelfand-Levitan-Marchenko type integral equations.A new formulation of solutions to special Riemann-Hilbert problems with the identity jump matrix，corresponding to the reflectionless inverse scattering transforms，is proposed and applied to construction of soliton solutions to each system in the considered nonlocal reversetime NLS hierarchies.

Key words matrix spectral problem;nonlocal reverse-time integrable equation;integrable hierarchy;Riemann-Hilbert problem;inverse scattering transform;soliton solution

1 Introduction

Nonlocal integrable equations are presented and analyzed by nonlocal reductions[1]，and their inverse scattering transforms were established under zero or nonzero boundary conditions[2-4].There exist five nonlocal integrable nonlinear Schrödinger (NLS) equations and modified Korteweg-de Vries (mKdV) equations.Soliton solutions to nonlocal NLS equations were generated from special Riemann-Hilbert problems with the identity jump matrix，corresponding to the re flectionless inverse scattering transforms，[5，6].Moreover，the Hirota bilinear method[7]and Darboux transformations[8-10]were applied to construction of exact solutions to nonlocal NLS and higher-order NLS equations.A few other nonlocal integrable equations[11-13]and multicomponent generalizations[14-16]were also proposed.

It is known that for integrable equations，the Riemann-Hilbert problems are generated from the associated matrix spectral problems and they are powerful in establishing inverse scattering transforms and presenting soliton solutions[17，18].Many integrable equations have been investigated through analyzing the corresponding Riemann-Hilbert problems.In this paper，we would like to construct a class of general nonlocal reverse-time NLS hierarchies of multicomponent equations，analyze their Riemann-Hilbert problems，and present soliton solutions through a new formulation of solutions to special Riemann-Hilbert problems with the identity jump matrix.

We will focus on the multicomponent AKNS spectral problem and its soliton hierarchy.For ease of reference，let us recall the multicomponent AKNS hierarchy.Let n∈N be arbitrary，In，the identity matrix of size n，α1，α2∈R，arbitrary but different constants.The multicomponent AKNS matrix spectral problem reads (see，e.g.，[19]):

where λ is a spectral parameter and u is a potential of dimension 2n:

When pj=qj=0，2≤j≤n，(1.1) reduces to the standard AKNS spectral problem[20].We assume[19]that a solution W to Wx=i[U，W]is given by

where b[m]，c[m]and d[m]，denoted by

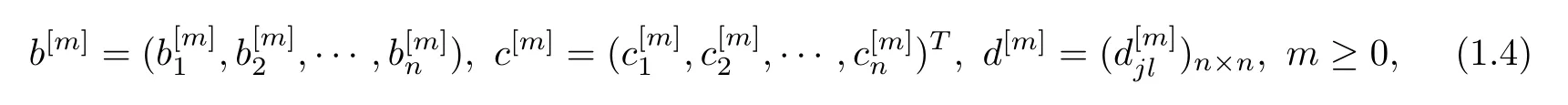
are defined recursively by

where α=α1-α2.Upon fixing the initial values:

β1，β2∈R being arbitrary but different constants，and by taking zero constants of integration in (1.5d)，i.e.，

the recursive relations in (1.5) determine a series of matrices Wm，m≥1，uniquely.In particular，we have

where β=β1-β2and 1≤j，l≤n.A recursion relation for b[m]and c[m]is found to be

where Ψ is a 2n×2n matrix operator

Upon introducing the following temporal matrix spectral problems

the compatibility conditions of (1.1) and (1.10)，

generate the so-called multicomponent AKNS soliton hierarchy:

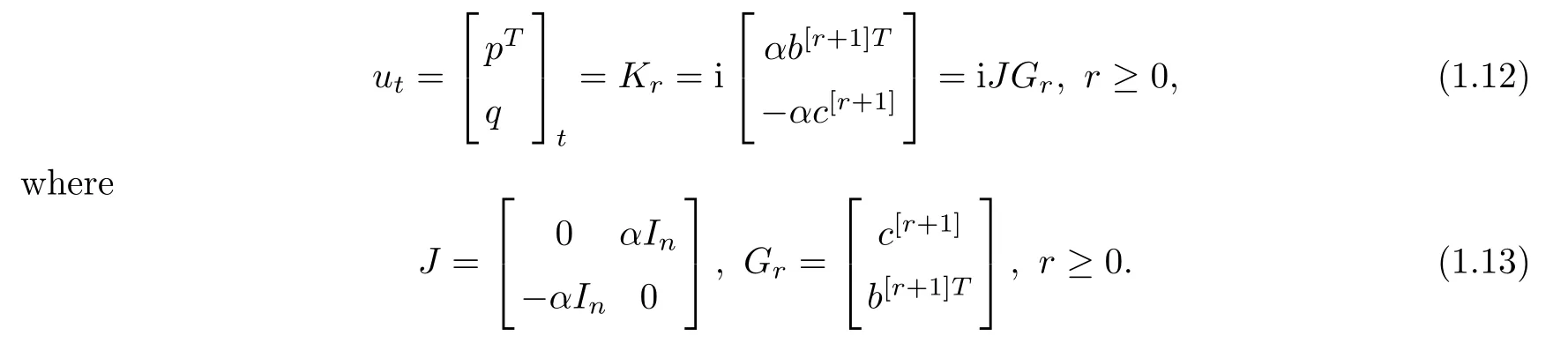
One of the nonlinear members (r=2) in the hierarchy (1.12) is the standard NLS equations:

The multicomponent AKNS soliton hierarchy (1.12) possesses a Hamiltonian structure，which can be established by applying the trace identity[21]，or more generally，the variational identity[22]:

where

The operator Φ=Ψ†provides a recursion operator for the whole hierarchy (1.12).For each r≥1，adjoint symmetry constraints (or a little bit loosely，symmetry constraints) transform the rth multicomponent AKNS equations into two commuting finite-dimensional Liouville integrable Hamiltonian systems，which generate involutive solutions[19，23].

The rest of the paper is structured as follows.In Section 2，we make a kind of nonlocal reductions to generate nonlocal reverse-time multicomponent NLS hierarchies.One of our examples of nonlocal coupled equations is as follows:

where c1and c2are arbitrary nonzero complex constants.In Section 3，we formulate Riemann-Hilbert problems from the associated matrix spectral problems.In Section 4，we analyze inverse scattering transforms via the presented Riemann-Hilbert problems.In Section 5，we construct soliton solutions through a new formulation of solutions to special Riemann-Hilbert problems with the identity jump matrix，namely，from the reflectionless inverse scattering transforms.In the final section，we give a conclusion and a few concluding remarks.

2 Nonlocal Reverse-time NLS Hierarchies

Motivated by the classical local reductions[24]，we consider a kind of nonlocal reductions for the spectral matrix U:

where

This means that

in which the potential matrix P is defined by

Here and in what follows，T stands for the matrix transpose，and Σ is an invertible constant symmetric matrix.For convenience，we also denote

for a matrix M depending on a function f.

Equivalently，(2.2) yields

Under such a kind of potential reductions，the vector function c in W can be taken as

and all those reduction relations guarantee that

where a and d are the other two entries of W.Therefore，we have

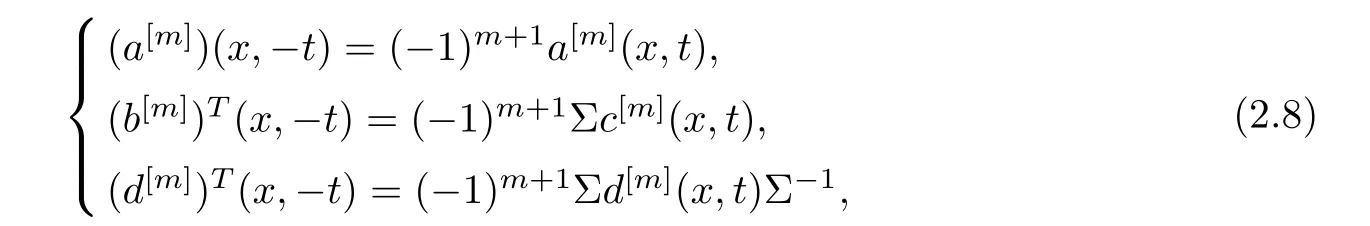
where m≥1.This implies that for all m≥1，we have

V[2m]being defined as in (1.10).

Now，based on (2.1) and (2.9)，it is direct to see that the nonlocal reductions in (2.2) do not raise any additional conditions on the compatibility of the previous spatial and temporal matrix spectral problems，when r=2m.Therefore，under the nonlocal reductions in (2.1)，the half hierarchy of the equations in the AKNS integrable hierarchy (1.12) with r=2m reduces to the following nonlocal reverse-time NLS hierarchies

in which the Lax pairs read

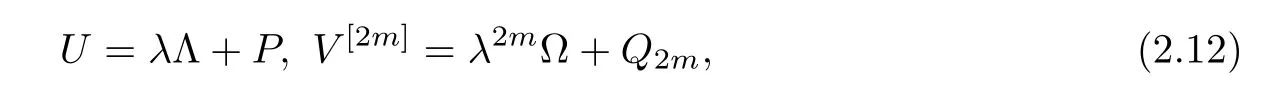
with Λ=diag (α1，α2In)，Ω=diag (β1，β2In)，and

Obviously，each system in (2.10) possesses an infinite hierarchy of commuting symmetriesand an infinite hierarchy of commuting conserved functionals

Moreover，if p (x，t) is a solution to any member in (2.10)，so are p*(x，-t) and p (-x，t).Hence，(2.10) is PT-symmetric.

When m=1，we obtain the multicomponent nonlocal reverse-time NLS equations[6]:

in which Σ is an arbitrary invertible constant symmetric matrix.Further，when n=1，we can obtain two well-known scalar examples:

where σ=±1，and when n=2，we can get a system consisting of two nonlocal reverse-time NLS equations:

where c1and c2are arbitrary nonzero complex constants.

3 Riemann-Hilbert Problems

Let q be determined by (2.5).In what follows，we formulate a class of Riemann-Hilbert problems associated with the matrix spectral problems of the nonlocal reverse-time NLS hierarchies，which will be the basis for inverse scattering transforms and soliton solutions.

3.1 Property of eigenfunctions

Let us assume that all the potentials sufficiently rapidly vanish when x→±∞or t→±∞.Upon setting=iP and=iQ2m，the equivalent pair of matrix spectral problems to (2.11) reads

Applying a generalized Liouville’s formula，we can obtain (detψ)x=0，due to=0.The adjoint equation of the x-part of (2.11) and the adjoint equation of (3.1) are determined by

There are links among the eigenfunctions φ，ψ and the adjoint eigenfunctions:

Let ψ(λ) be a matrix eigenfunction of the spatial spectral problem (3.1) associated with an eigenvalue λ.Then，Cψ-1(x，t，λ) is a matrix adjoint eigenfunction associated with the same eigenvalue λ.Moreover，under the nonlocal reductions in (2.2)，we can compute that

and so we find that

gives another matrix adjoint eigenfunction associated with the same original eigenvalue λ，i.e.，ψT(x，-t，-λ) C solves the adjoint spectral problem (3.4).

Therefore，upon noting the asymptotic behaviours for ψ，the uniqueness of solutions determines that

if ψ→In+1when x or t→∞or-∞.It then follows that if λ is an eigenvalue of (3.1)(or (3.4))，then-λ will be another eigenvalue of (3.1)(or (3.4))，and the property (3.7) holds.

3.2 Riemann-Hilbert problems

We now formulate a class of associated Riemann-Hilbert problems with the variable x.In order to express the computation below，let us also assume that

In the scattering problem，we first introduce the two matrix eigenfunctions ψ±(x，λ) of (3.1) with the asymptotic conditions

respectively.It follows from (detψ)x=0 that detψ±=1 for all x∈R.Since both

solve (2.11)，they must be linearly dependent，and as a consequence，we have

where S (λ) is traditionally called the scattering matrix.We point out that detS (λ)=1 because of detψ±=1.

Through the method of variation in parameters，we point out that we can turn the x-part of (2.11) into the following Volterra integral equations for ψ±[17]:

where the asymptotic conditions (3.9) have been imposed.Now，the theory of Volterra integral equations can show that the eigenfunctions ψ±could exist and allow analytical continuations offthe real line λ∈R provided that the integrals on the right hand sides converge.It can be seen that the first column of ψ-and the last n columns of ψ+are analytical in the upper half-plane C+and continuous in the closed upper half-plane，and that the last n columns of ψ-and the first column of ψ+are analytical in the lower half-plane C-and continuous in the closed lower half-plane.

Then，on one hand，to determine two generalized matrix Jost solutions (a kind of combinations of matrix Jost solutions)，T+and T-，which are analytic in C+and C-(the upper and lower half-planes) and continuous inand(the closed upper and lower half-planes)，respectively，we state

On the other hand，to determine the other generalized matrix Jost solution T-，we construct the analytic counterpart of T+in the lower half-plane C-from the adjoint matrix spectral problems.It is known that the inverse matrices=(φ±)-1and=(ψ±)-1solve those two adjoint equations，respectively.Therefore，similarly，upon statingas

which is analytic for λ∈C-and continuous for λ∈.

Let us now construct two unimodular generalized matrix Jost solutions from T+and T-.Based on detψ±=1 and the scattering relation (3.11) between ψ+and ψ-，we can derive

Therefore，two unimodular generalized matrix Jost solutions can be taken as

which formulate the associated matrix Riemann-Hilbert problems on the real line for the nonlocal reverse-space multicomponent NLS equations (2.14).Those required matrix Riemann-Hilbert problems read:

where by (3.11)，the jump matrix G0is given by

In the above jump matrix G0，the matrixhas the factorization:

which can be explicitly computed as follows:

Again from the Volterra integral equations (3.12) and (3.13)，we can obtain the canonical normalization conditions:

for the presented Riemann-Hilbert problems on the real line.

4 Inverse Scattering Transforms

We analyze inverse scattering transforms for the nonlocal reverse-time NLS hierarchies (2.10) through the associated Riemann-Hilbert problems established above.

4.1 Time evolution of the scattering data

To complete direct scattering transforms，we compute the derivative of (3.11) with time t to obtain

and take use of the temporal matrix problems that ψ±satisfy:

It then follows that the scattering matrix S needs to satisfy an evolution law:

This yields the time evolution of the time-dependent scattering coefficients:

but all other scattering coefficients do not depend on the time variable t.

4.2 Relations of the reflection coefficients

The jump matrix G0carries basic scattering data from the scattering matrix S (λ).By the property of eigenfunctions in (3.7)，one has

Therefore，the jump matrix G0satisfies the following involution property

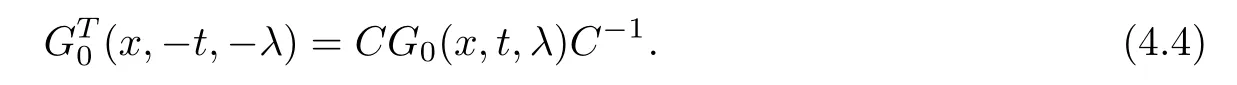
This exhibits relations between the reflection coefficients.

4.3 Gelfand-Levitan-Marchenko type equations

To obtain Gelfand-Levitan-Marchenko type integral equations for the generalized matrix Jost solutions，we transform the associated Riemann-Hilbert problems in (3.21) into

Let G (λ)=G±(λ) if λ∈C±.Suppose that G has simple poles offthe real line R:，and thus there is no spectral singularity，where R is an arbitrary natural number.Introduce

where Gjis the residue of G at λ=μj，i.e.，Gj=.Then，we obtain

By applying the Sokhotski-Plemelj formula[25]，we get the solutions

Then，taking the limit as λ→μlgenerates the required Gelfand-Levitan-Marchenko type integral equations:

These equations are used to determine solutions to the associated Riemann-Hilbert problems，and hence，the generalized matrix Jost solutions.The general theory of existence and uniqueness of solutions is yet to be developed.In the following section，we will present a formulation of solutions to specific Riemann-Hilbert problems with the identity jump matrix，which can be applied to nonlocal integrable equations.

4.4 Recovery of the potential

In order to recover the potential matrix P from the generalized matrix Jost solutions，we make an asymptotic expansion

Plugging this into the matrix spectral problem (3.1) and comparing O (1) terms engenders

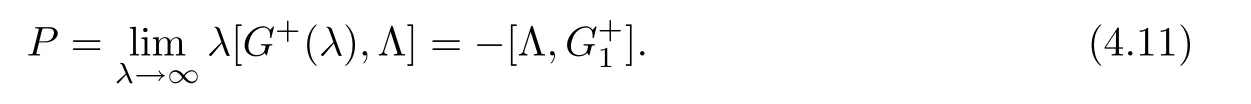
One needs to check an involution property for:

Then，solutions to the nonlocal reverse-time NLS hierarchies (2.10) will be determined by

Those constitute an inverse scattering procedure from the scattering matrix S (λ) through the jump matrix G0(λ) to the potential matrix P.The final resulting potential P determines solutions to the nonlocal reverse-time NLS hierarchies (2.10).

5 Soliton Solutions

Let N∈N be arbitrary.Suppose that detT+(x，λ)=s11has zeros{λk∈C，1≤k≤N}，and detT-(x，λ)=has zeros{∈C，1≤k≤N}.We also assume that all these zeros are geometrically simple.Thus，each kerT+(λk) contains only a single basis column vector，denoted by vk;and each ker，a single basis row vector，denoted by.This way，one has

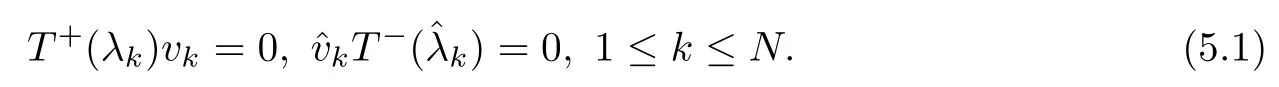
Soliton solutions are associated with G0=In+1in the Riemann-Hilbert problems，achieved under zero reflection coefficients:si1==0，2≤i≤n+1.Solutions to this kind of special Riemann-Hilbert problems can be formulated in the case of local integrable equations (see，e.g.，[17，26，27]).However，in the case of nonlocal integrable equations，we often do not have the condition

and thus we need a new formulation of solutions to the above special Riemann-Hilbert problems.A direct check shows that the solutions can be presented as follows:

where M=(mkl)N×Nis a square matrix whose entries are determined by

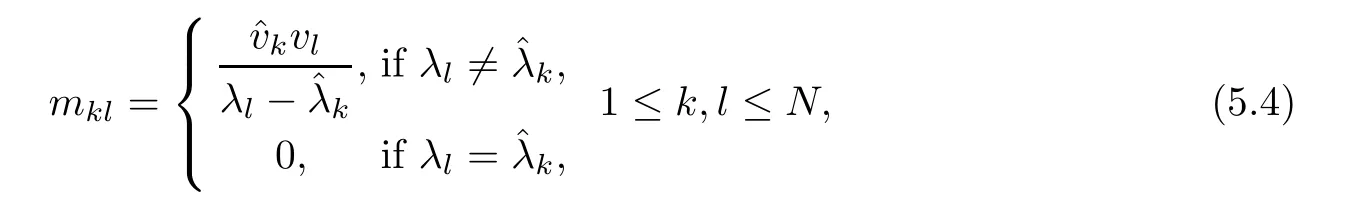
for which an additional orthogonal condition is required:

which ensures that

To satisfy the involution property (4.12)，we take zeros of detT+(λ) and detT-(λ) as follows:

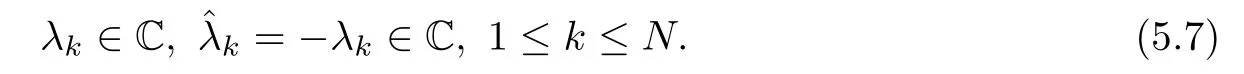
Then，kerT+(λk) and kerT-(λk)，1≤k≤N，are determined by

respectively.Here wk，1≤k≤N，are arbitrary constant column vectors but need to satisfy

which follows from the orthogonal condition (5.5).

Finally，we see under (5.7)，(5.8)，(5.9) and (5.10) that the solutions to the special Riemann-Hilbert problems，determined by (5.3) and (5.4)，satisfy (4.3)，which implies thatsatisfies (4.12).Therefore，N-soliton solutions to the nonlocal reverse-time NLS hierarchies (2.10) are given by

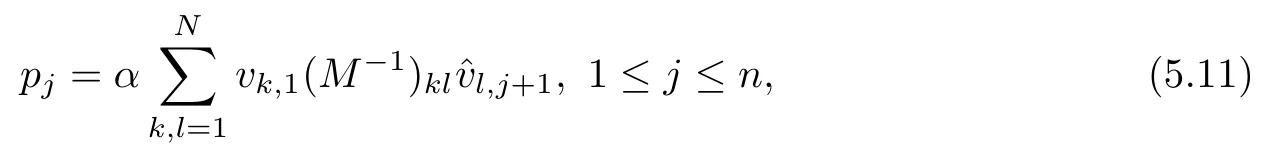
where M is determined by (5.4)，and

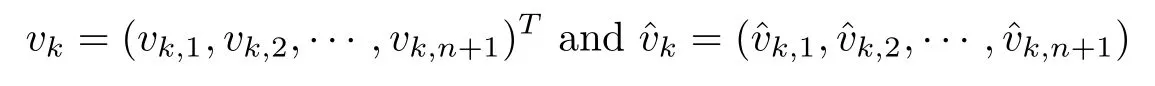
are defined by (5.8) and (5.9)，respectively.

When m=N=1，upon denoting Σ=diag (γ1，···，γn)，(5.11) presents the following one-soliton solution to the nonlocal reverse-time NLS equations (2.14):

where w1=(w1，1，w1，2，···，w1，n+1)T∈Cn+1and λ1∈C are arbitrary，and γ1，···，γn∈C are arbitrary but nonzero.This solution is analytic on the real line of x at any time when the factorof the denominator is either positive or negative，but it has time-independent singularity otherwise and so it has analytic solutions if the problem is restricted to an interval which excludes that singularity point.

6 Concluding Remarks

We considered a class of higher-order degenerate AKNS spatial matrix spectral problems，generated the corresponding nonlocal reverse-time multicomponent NLS hierarchies，and analyzed their inverse scattering transforms and soliton solutions.The analysis is based on Riemann-Hilbert problems generated from the associated matrix spectral problems.The Sokhotski-Plemelj formula was used to transform the Riemann-Hilbert problems into Gelfand-Levitan-Marchenko type integrable equations to determine unimodular generalized matrix Jost solutions，and soliton solutions of the multicomponent nonlocal reverse-time NLS hierarchies were constructed from the reflectionless inverse scattering transforms.

We remark that it would be interesting to see how to construct different kinds of exact solutions in nonlinear dispersive waves，for example，lump solutions[28-30]，Rossby wave solutions[31]，solitonless solutions[32-34]，algebro-geometric solutions[35，36]and dromions[37，38]，through the Riemann-Hilbert technique.Any connection from Darboux transformations to explicit solutions to special Riemann-Hilbert problems with the identity jump matrix should be important.It is also expected that we could have a clear picture about soliton solutions to local and nonlocal integrable counterparts，such as integrable couplings，super hierarchies and fractional analogous equations，from a perspective of the Riemann-Hilbert technique.