基于最小二乘曲线拟合提取基频分量

牛智锐，宋运忠

（河南理工大学 电气工程与自动化学院，焦作 454003)

0 引言

输电线路监测到的故障中80%是单相接地故障，而瞬时故障占其中的50%～90%[1]。瞬时故障是指在线路上仅持续几个周期的暂时性故障。虽然瞬时故障能够在一定延时后重合成功，产生的故障电弧熄灭后不会对电力系统和电气设备造成重大损坏，但是这些故障通常是同一位置发生永久性故障的前兆[2，3]。瞬时故障造成电流巨大变化，电路中的电感会阻碍电流的变化，产生随时间呈指数衰减的直流偏移分量。直流偏移分量对基频相量的提取造成影响，导致故障定位产生较大的误差。

如何快速消除直流偏移分量并准确地提取基频分量，一直是国内外学者研究的热点问题。采用全波和半波傅里叶算法提取故障信号的基频分量，存在计算时间长、响应速度慢、无法完全滤除直流偏移分量的缺点[4～6]。使用同步相量估计算法[7，8]修正离散傅里叶变换（Discrete Fourier Transform，DFT）可以较好的消除直流偏移分量提取基频分量，缺点是计算量较大。文献[9]将Hilbert变换与DFT相结合计算基频相量，该算法的计算过程非常复杂。文献[10]先对输入的电流信号进行积分，然后在每个采样瞬间减去衰减的直流偏移分量获得基频相量。该算法将故障持续一个周期后的采样数据用于计算，其难点在于必须能够准确地检测出故障的起始时间。文献[11]需要2.25个周期的波形数据，将经验模态分解与Hilbert变换相结合计算基频相量。算法易受波形周期的限制，不适合应用于继电保护。使用最小二乘算法[12]消除直流偏移分量提取基频相量，算法的性能会随着时间常数的减小而降低，难以满足电力系统对于稳定性的要求。

针对上述方法存在数学模型较为复杂、运算量较大的缺点，本文构建新的数学模型提取基频分量。利用均方根域-小波变换方法获取完整的故障时间段数据，使用非线性最小二乘曲线拟合提取基频分量。通过多个算例的仿真验证和分析，算法能够快速准确地提取基频分量。将其应用于继电保护装置开展故障定位研究工作，可以很好的与行波法[13～16]相互补充，更好地保障输电系统的安全、可靠运行。

1 构建故障信号数学模型

当输电系统发生单相接地故障时，电流产生衰减的直流偏移分量。将故障电流信号看作由一个含有谐波的交流分量iAC和一个随时间常数呈指数衰减的直流偏移分量iDC组成[17]：

式中，直流偏移分量初始时刻的大小取决于故障时刻的入射角θn，直流偏移分量的衰减时间常数取决于系统在故障点的比值X/R。

实际上，谐波成分比较复杂，系统发生单相接地故障，其幅值与基频分量相比很小，谐波只会造成数据的离散并不能改变基频信号的趋势。基于最小二乘曲线拟合方法构建拟合函数，将故障电流信号表示为一个对称的正弦基频交流分量和一个随时间常数呈指数衰减的直流偏移分量：

2 故障仿真实验与基频分量提取算法

本节在MATLAB/Simulink仿真环境下搭建如图1所示的双端电源系统输电线路单相接地故障仿真模型，仿真模型参数为：两端电源电压EG=220∠30°kV、EH=220∠0°kV，系统频率50Hz，输电线路总长度300km，设置单相接地故障点F距G端150km，两端电源内阻ZG=1.06+j44.92Ω、ZH=1.05+j43.18Ω，线路正序阻抗Z1=0.02083+j0.282Ω/km，线路零序阻抗Z0=0.1148+j0.7186Ω/km。仿真时间0.2s，采样频率为5kHz，即每个周波采样100点。

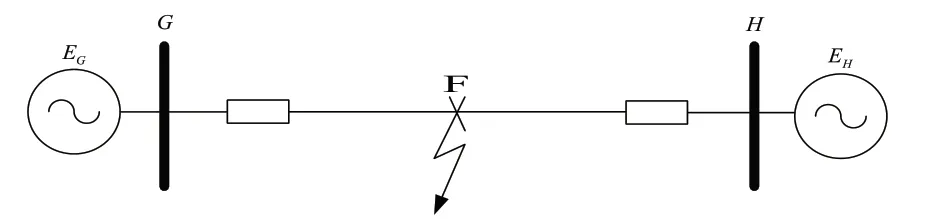
图1 输电线路故障模型

过渡电阻为零时，在监测位置G记录的三相电流和电压波形如图2所示。

图2 记录电压和电流波形

2.1 检测故障信号

系统发生单相接地故障，微机继电保护装置通过阻抗继电器的视在阻抗或过流继电器的均方根电流与预先设定好的阻抗域或继电器吸合电流作比较来检测故障。上述两种方法将窗口时域波形转换为阻抗复数平面[18]或均方根域，能够成功地检测故障发生和故障清除。

基于过流继电器的工作原理，设定两倍的均方根电流作为过流继电器预先设定的均方根域。如图3所示，故障电流信号首次超过均方根域时检测到故障发生，对应的故障起始时刻为0.0612s；故障电流信号末次高于均方根域后故障清除，对应的故障清除时刻为0.1404s。

图3 均方根域检测故障电流

2.2 获取完整的故障时间段数据

获取完整的故障时间段数据应用于提取基频分量有两个优点：1）当故障持续时间较短、特别是小于一个周期时，因为故障数据点较少，所以使用完整的故障时间段数据提取基频分量准确度更高。2）能够最大限度地减少非故障期间数据点。

本文以均方根域检测到的故障时刻为依据，将常见的时频域分析工具小波变换应用于暂态电能质量分析中，能够准确地检测与定位故障信号的起止时刻与持续时间。当小波变换应用于电能质量检测时，小波基的选取是一项重要的工作，文献[19]和文献[20]提出db小波是检测电能质量扰动的一个很好的选择。如图4所示，当故障电流信号首次超过均方根域，检测到故障发生。选择小波系数能量集中的db4为小波基进行小波变换，平方小波变换系数最大值对应的0.0608s为校正后的故障起始时刻。当故障电流信号末次高于均方根域后，故障清除，采用同样的方法得到校正后的故障清除时刻为0.1438s。

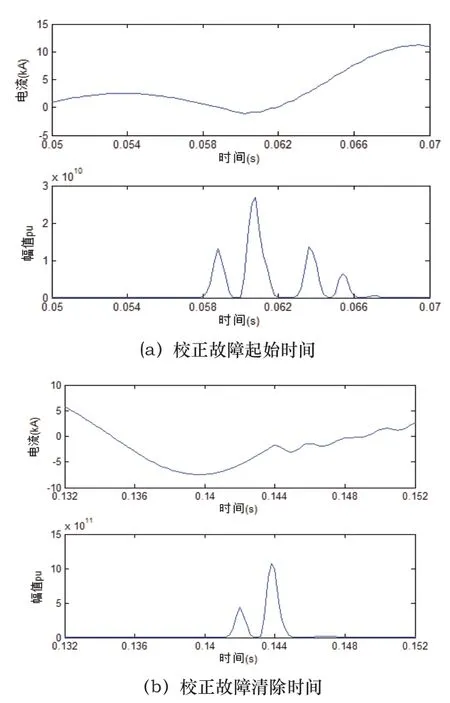
图4 使用db4小波变换校正故障时间

故障持续时间为0.0830s，提取完整的故障发生时段电流信号如图5所示。

图5 获取的故障电流信号

2.3 求解模型参数

根据计算机数值计算的需要，引出向量a=(β1，β2，β3，β4)表示模型参数，式(2)改写为：

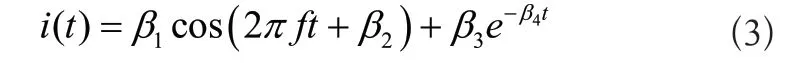
式中：β1=A1表示对称的基频交流分量幅值，单位A；β2=θ1表示对称的基频交流分量初相位，单位rad；β2=B表示指数衰减的直流偏移分量幅值，单位A；β4-1=-ω/(X/R)表示指数衰减的直流偏移衰减常数，单位s-1。

通过对故障信号电气量特点的分析，将故障时刻ti对应的单相接地故障电流vi进行曲线拟合求解模型参数。式(4)定义有约束的最小二乘目标函数：使用信赖域反射法[21～23]求解式(4)，得到基频分量β1cos(2πfti+β2)和直流偏移分量β3e-β4ti。

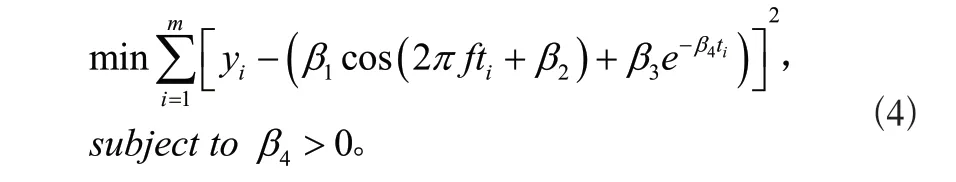
2.4 提取电气量

本文针对以下四种典型的故障情况按照上述步骤进行分析：理想情况下的单相接地短路故障、含有谐波分量的单相接地故障、持续时间小于一个周期的单相接地短路故障和存在过渡电阻的单相接地故障。

2.4.1 单相接地短路故障

理想情况下的单相接地短路故障曲线拟合结果如图6所示，基频分量提取结果如表1所示。

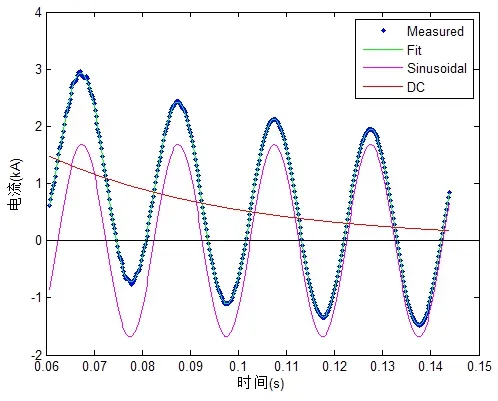
图6 分解故障电流

2.4.2 含有谐波分量的单相接地短路故障

电网中由于正弦电压加压于非线性负载，导致电流发生畸变产生谐波，一般以3，6n±1次谐波较为常见。其中，3次谐波是主要成分之一且幅值最大，对继电保护和设备的冲击最强，对电网的影响也最为严重。

在故障信号中分别添加不同类型的谐波分量，其幅值为基波幅值的10%，基频分量参数提取结果如表1所示。

表1 含有不同谐波分量的计算结果

将3，5，7，11，13，17，19次谐波同时添加至故障电流信号，改变谐波幅值，基频分量参数提取结果如表2所示。

表2 不同幅值时的计算结果

当谐波幅值为基波幅值的30%，曲线拟合结果如图7所示。

欧拉iQ高续航版也在车展现场上市，其综合续航里程达401公里，不同配置车型补贴后售价分别为9.28万元、9.98万元和10.88万元。与此同时，欧拉还对外发布了汽车新零售平台“欧拉ORA”超级APP。“欧拉ORA”超级APP可实现线上下单功能，资讯、话题和社区等线性连接功能，与欧拉粉丝建立起立体连接。

图7 分解含有谐波分量的故障电流

由表1可知，当故障信号只含有5次谐波时，基频分量幅值的误差最大；随着谐波次数增大，误差逐渐减小。当故障信号只含有3次谐波时，基频分量初相位的误差最大；随着谐波次数的增大，误差减小。由表2可知，当故障信号中含有多个谐波分量时，随着谐波幅值的逐渐增大，提取的基频分量幅值和初相位的误差也逐渐增大。

然而，即使使用含有多个谐波分量且谐波幅值为基波幅值30%的故障信号提取基频分量参数，基频分量幅值和初相位的误差也仅为-0.2521%、0.2088%。拟合出的基频分量参数与无谐波时相比误差很小，证明本文建立的最小二乘函数模型能够较好的抑制谐波分量，基频分量提取精度较高。

2.4.3 持续时间小于一个周期的单相接地短路故障

微机继电保护装置使用傅里叶滤波器提取基频相量需要一个周期的波形数据。如图8(a)所示，当故障持续时间小于一个周期，故障期间和故障结束后的数据点都将应用于傅里叶滤波器，导致提取的基频分量精度降低、故障定位误差增大。曲线拟合结果如图8(b)所示，电气量提取结果如表3所示。

图8 故障持续时间不足一个周期

2.4.4 存在过渡电阻的单相接地故障

当单相接地故障存在过渡电阻时，随着过渡电阻阻值增大，系统中出现直流偏移分量的可能性逐渐减小。由于阻值的增加降低了故障期间的X/R值，所以产生的直流偏移分量衰减速度快。

设定过渡电阻为50Ω时系统发生单相接地故障，故障仿真信号如图9(a)所示，曲线拟合结果如图9(b)所示，电气量提取结果如表3所示。

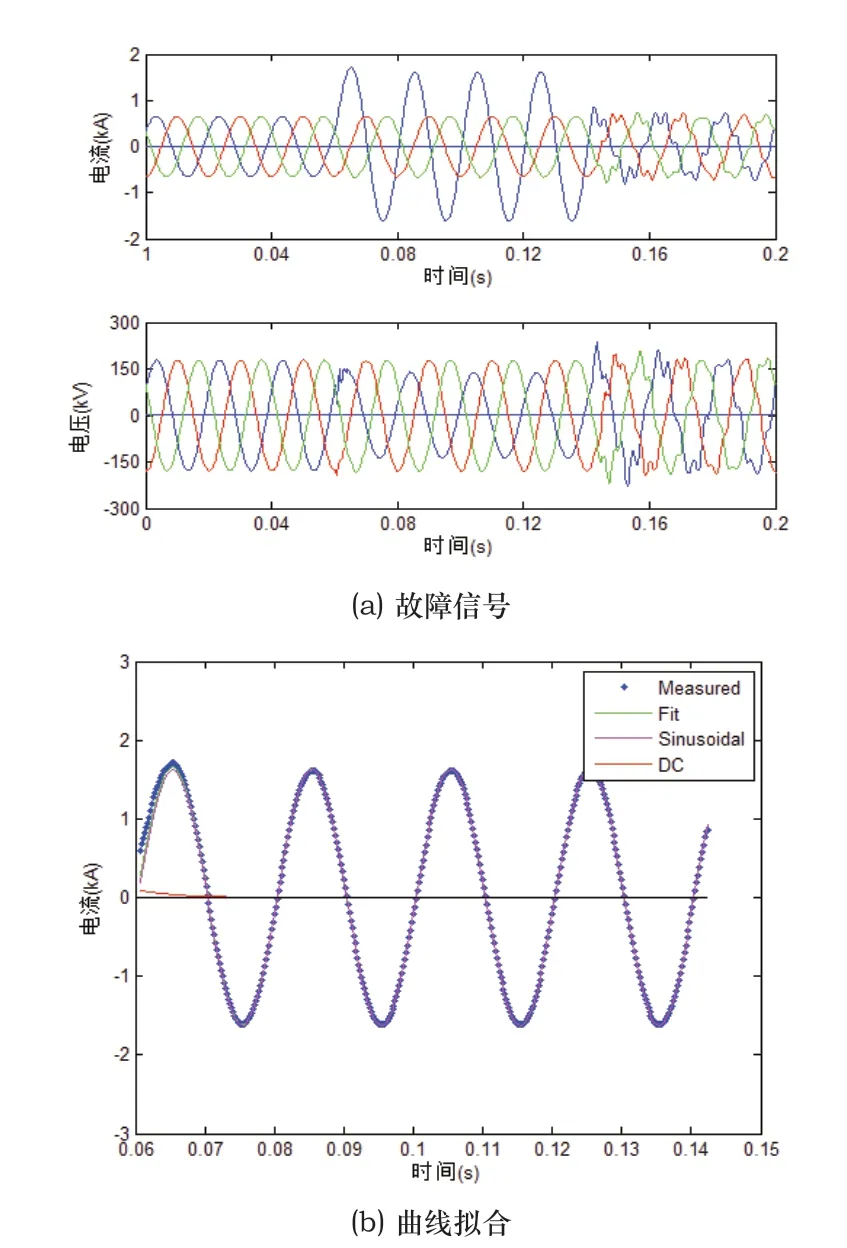
图9 存在过渡电阻的单相接地故障

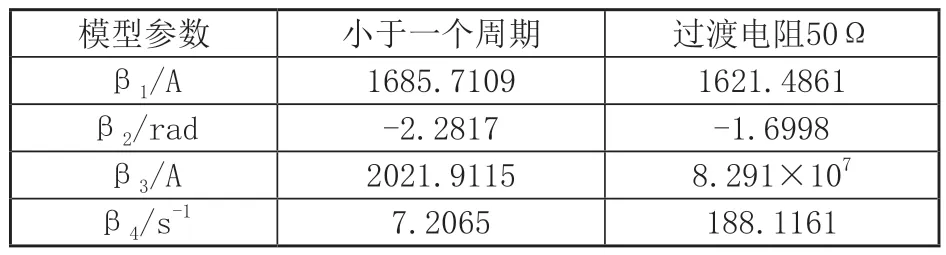
表3 不同情况的计算结果

3 算法验证分析

微机继电保护装置基于阻抗法的Takagi方法计算从监测点到故障位置的距离：

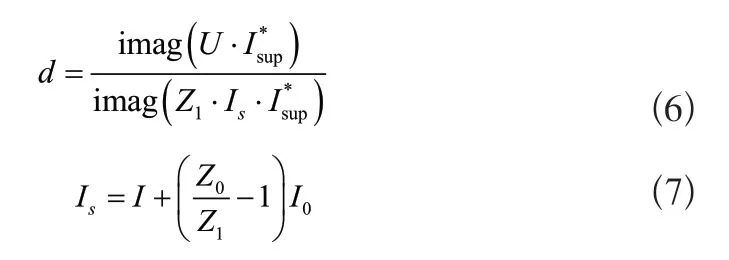
式中，U表示母线电压降，I表示故障电流，Iper表示故障前的电流，I0表示零序电流，Z1为线路正序阻抗，Z0为线路零序阻抗，*表示共轭复数。

同时，故障定位结果误差定义如下：

本节通过故障定位结果，验证在上述四种典型的故障情况下提取基频分量的准确性。

3.1 含有谐波分量的单相接地短路故障

由表4可知，含有谐波分量的单相接地短路故障的故障定位误差很小，说明提取的基频分量鲁棒性强、准确度高，能够很好的消除单相接地故障产生的直流偏移分量。

3.2 故障持续时间小于一个周期的单相接地短路

经计算，与单相接地短路故障相比误差增大。主要原因有两点：1）采样点数据较少会导致基频相量计算结果误差增大。2）故障数据中参杂了非故障期间的数据点。

3.3 存在过渡电阻的单相接地故障

由表4可知，单相接地故障存在过渡电阻时，与单相接地短路故障相比误差增大。此时，误差源自Takagi方法假设系统是均匀的，故障点两端的故障电流分量相位角一致[24]。然而，在仿真环境下系统是非均匀的，违反假设导致误差增大。但是算法可以避免提取基频相量时造成额外误差的情况，基频分量提取结果准确度较高。

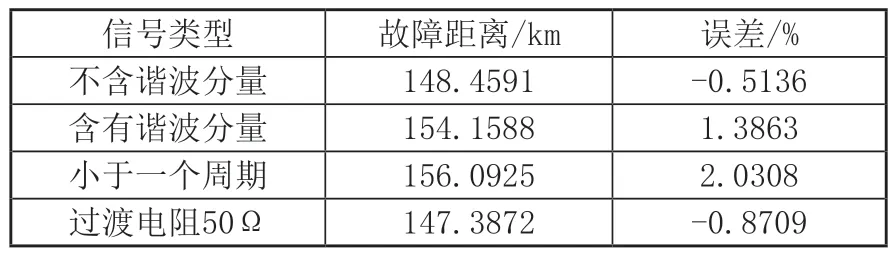
表4 故障距离和误差

4 结语

本文构建的故障信号数学模型能够快速消除单相接地故障产生的直流偏移分量、准确提取故障信号基频分量，故障定位结果精度较高。数学模型具有以下四个优点：

1）运用函数逼近原理，把故障信号看作基频交流分量和直流偏移分量相叠加，使用数学表达式直接消除直流偏移分量，提取基频分量更加简单。

2）数学模型通常在10～200次迭代后提取基频分量，算法拥有快速高效的计算效率。

3）谐波分量对现有数学模型拟合出的基频相量影响很小，对谐波分量有较好的抑制作用。

4）可以计算任意时长瞬时故障信号包含的基频相量，算法不受波形周期的限制，准确度较高。