半地下贮液池结构抗震分析方法的修正系数研究*

毕继红 段逸辰 霍琳颖 王照耀

1.天津大学建筑工程学院 300350

2.滨海土木工程结构与安全教育部重点实验室（天津大学） 300072

引言

在地震作用下，钢筋混凝土贮液池可能发生多种震害现象，包括池内辅助结构破坏、侵蚀破坏、局部失稳、材料破坏以及池壁破坏等震害［1］，目前，地下结构的抗震性能分析方法大体可分为两大类，即动力时程分析法和拟静力分析法［2］，时程分析法计算精度较高，可以准确反应结构随时间的变化，但动力时程分析法计算量较大、耗时多，且在地震输入、人工边界处理等方面增加问题的复杂度，计算结果也易受地震波选取的影响［3］。因此在一般工程问题中应用较少。拟静力法分析相对简单、计算量相对较小，但难以得到结构在地震动过程中的动态变化。

对于地下贮液池的抗震分析方法，国内外许多学者进行了大量的研究。Shukla等［4］应用弹性地基梁原理，采用拟静力法来考虑土体与结构的相互作用；Seeber、Fischer［5］通过建立三维有限元模型研究了地震波下的液-池-土的相互作用。自由场变形法是由Newmark在20世纪60年代提出［6］，后经C.M.St.John和T.F.Zahrah［7］发展起来的一种简单有效的抗震分析方法，该方法将地震作用下结构位置处的自由场变形作为结构的变形直接施加到地下结构上计算结构的地震响应。

我国研究人员刘杰平等［8］采用ANSYS有限元软件分析了固液耦合作用的钢筋混凝土矩形水池动力响应，得到了影响水池抗震性能的影响因素。张聪［9］在两阶段设计法、应答震度法、抗震计算和耐震检测方法的基础上，对某净水厂地下储液池的抗震计算进行了全过程分析整理，赵杰等［10］以反应位移法对核电厂工业水池抗震设计分析，通过ANSYS的二次开发并结合五点公式计算得到结构内力分布规律及其危险工况。

该贮液池结构复杂，进行时程分析法时工作量大，计算时间长，为了对比拟静力法与时程分析法两种抗震分析方法计算结果，本文建立了结构的有限元简化模型，以相同的边界条件与加载方式对模型采用拟静力法与时程分析法两种方法进行计算，得到两种分析方法的计算结果，提出了一个修正系数使两种抗震方法的计算结果可以转换，在此基础上对结构进行抗震分析。

1 工程概况

1.1 结构概况

本贮液池建于1979年，贮液池由流入室、沉沙池组成，贮液池上部存在附属结构。贮液池的地表面标高为4.00m，地下水位为-2.30m，贮液池底板标高为-21.38m。贮液池长30m，宽17m，流入室与沉沙池由1000mm厚的钢筋混凝土板分隔，流入室与沉沙池之间的分隔板存在两个4.4m×2.5m的矩形水口。沉沙池为地下四层结构，长19.5m，宽17m，底部一层为10.75m高的沉沙池，负一至负三层为设备及人员室共18.5m高。流入室为地下两层结构长17m，宽10.5m，底部一层为16.25m高的流入池，负一层为楼梯间及瞭望台。由于结构复杂，给出结构剖面图，如图1所示。

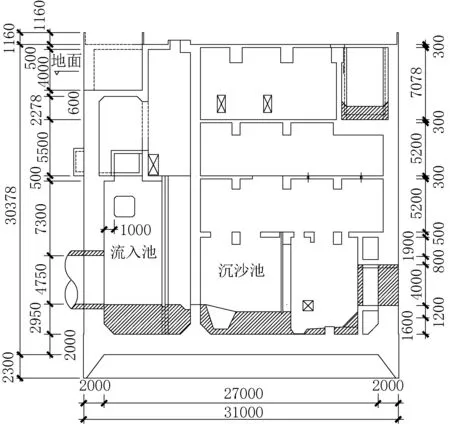
图1 半地下贮液池剖面图（单位：mm）Fig.1 Sectional view of semi-underground reservoir（unit：mm）

贮液池基础为群桩基础，由50根桩径1500mm，桩长为32.5m的单桩组成，群桩基础平面布置如图2所示。

图2 群桩基础平面布置图（单位：mm）Fig.2 Layout drawing of pile group foundation（unit：mm）

1.2 边界条件

贮液池周围土体由回填土、第一黏土层、第一砂土层、第二黏土层、第三黏土层组成。各层土体分别记作Bs、Ac1、As1、Ac2、Ac3参数见表1。

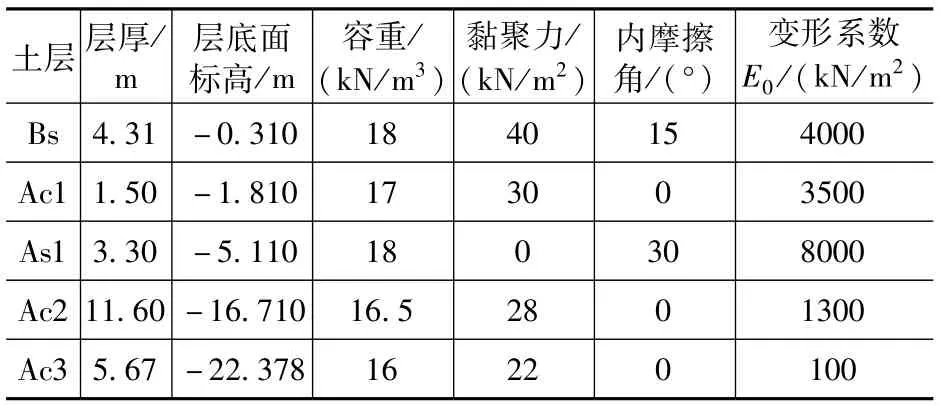
表1 各层土体参数Tab.1 Soil parameters of each layer

2 有限元模型的建立

用有限元分析软件FINAL对结构进行建模，结构采用四边形板单元，以弹簧单元代替侧板和底板周围的土体，结构受力以面力加载至板单元，由于实际有限元模型结构复杂，难以进行动力时程分析，故建立一个简化结构的有限元模型，对简化模型分别采用动力时程法与拟静力法进行计算，得到结构的最大响应，如图3、图4分别为实际结构的有限元模型与简化结构的有限元模型。

2.1 实际结构有限元模型

依据结构建立实际有限元模型如图3所示，模型详细还原了结构的全貌，模型共有21849个板单元，21607个节点。梁与柱使用加厚的板单元进行计算，结构各个板各方向的配筋，通过配筋率赋予板单元。

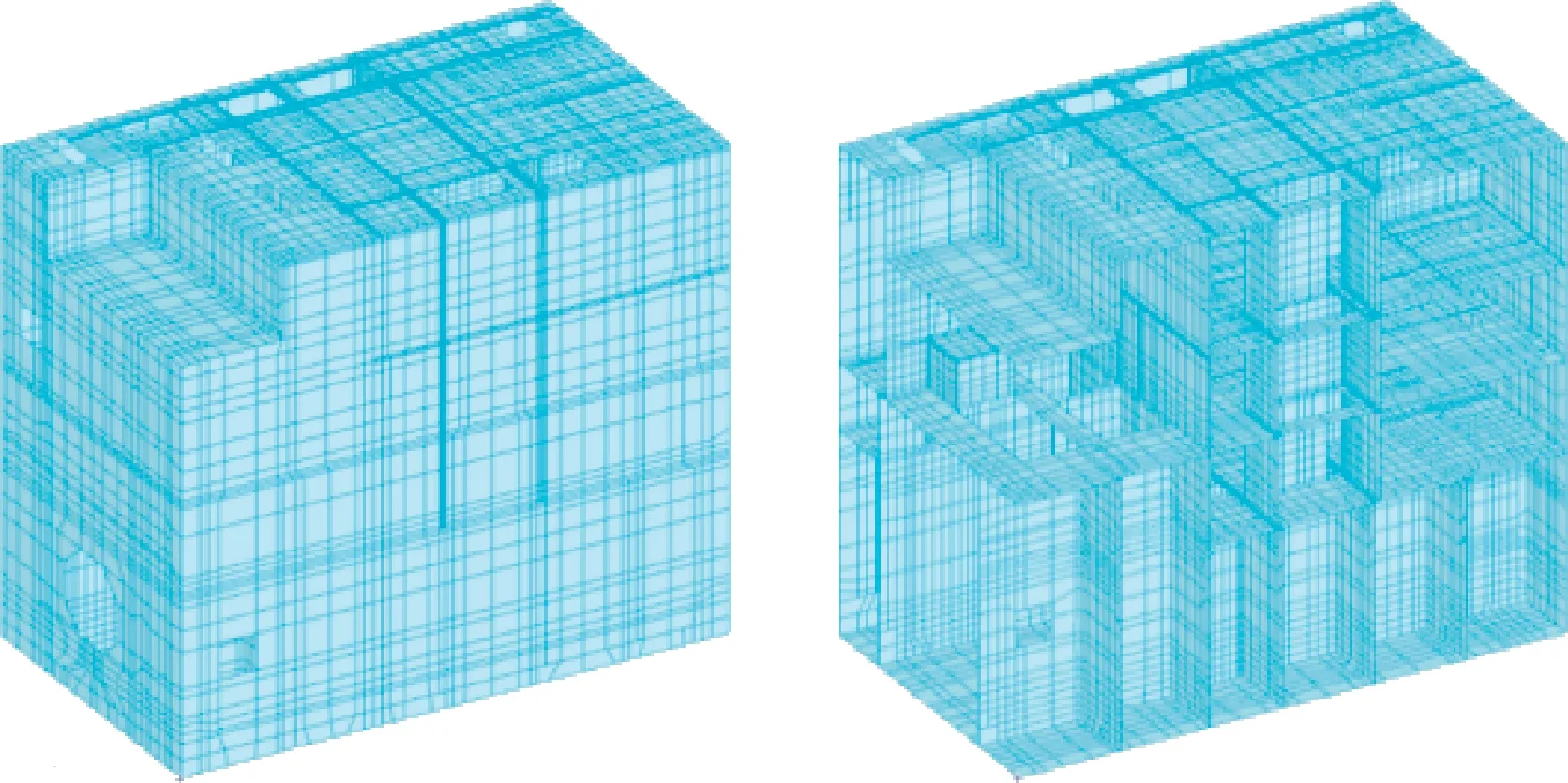
图3 实际结构有限元模型Fig.3 Finite element model of actual structure

2.2 简化结构有限元模型

由于结构单元节点数量多，对结构进行动力时程分析方法计算量大，耗时久，故建立结构的简化模型如图4所示。采用动力时程法与拟静力法进行抗震性能分析。

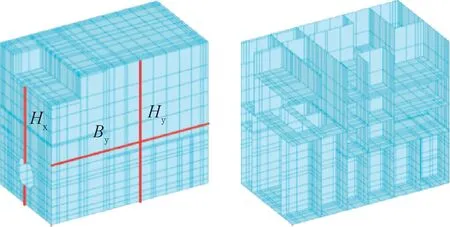
图4 简化结构有限元模型Fig.4 Simplified structural finite element model

简化结构依据实际结构忽略非关键部分减少单元数，对网格进行合理放粗减少计算量，为了保证简化结构的有限元模型具有足够的计算精度。简化结构有限元模型与实际结构有限元模型采用相同的边界条件、荷载组合与配筋，以相同的加载方式对简化结构有限元模型进行计算，使简化结构有限元模型与实际结构有限元模型最大相应出现的位置相同，最大响应值的误差也在合理范围内，以确保简化结构有限元模型的计算精度，网格放粗以后的有限元模型共有4735个板单元，4322个节点。

2.3 材料本构

1.混凝土本构

混凝土受压本构采用Saenz［11］模型，由式（1）表示：

式中：σc为混凝土压应力，ε1为应变；Ec为变形模量；Es为弹性模量；εc为峰值压应变。

混凝土受拉采用线弹性本构模型，开裂后应力为零［12］。

2.钢筋本构

钢筋本构采用理想弹塑性模型，由式（2）表示：

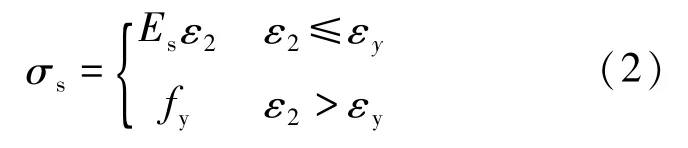
式中：σs为钢筋应力；ε2为钢筋应变；fy为钢筋屈服强度；εy为钢筋屈服应变；Es为弹性模量。

3 边界条件

3.1 侧板地基反力系数

贮液池地面以下的周围土体选用弹簧单元代替，赋予弹簧单元水平地基反力系数kH与切向地基反力系数kV，地基反力系数计算公式采用日本土木学［13］会给出的公式，侧壁水平地基反力系数见表2。

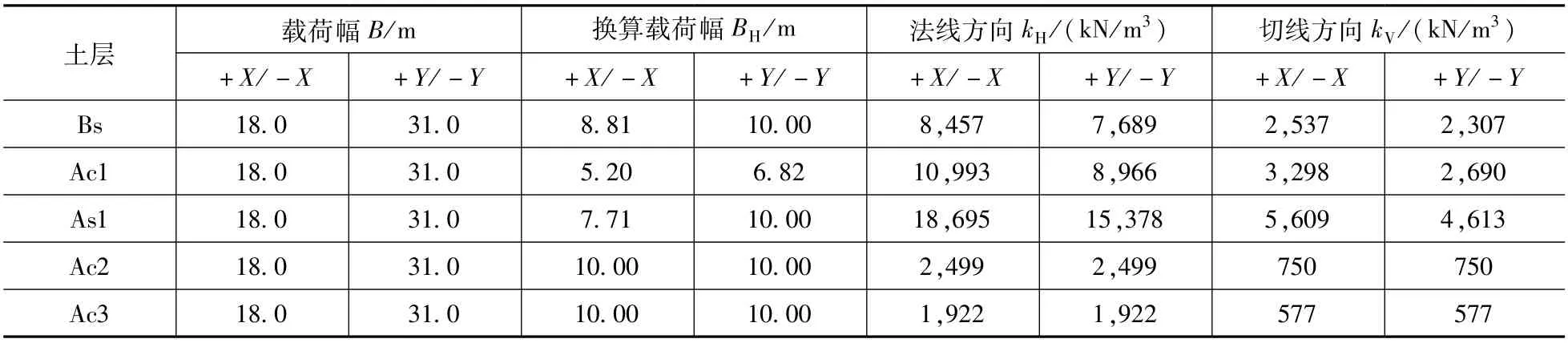
表2 地基侧板弹簧计算结果Tab.2 Calculation result of side leaf spring on foundation

水平地基反力系数kH：

切向地基反力系数kv：

式中：α为地基反力换算系数，通过孔内水平荷载试验测定，在地震时取常数8；E0为地基变形系数；BH为与荷载作用方向垂直的基础换算载荷幅，由计算，B为荷载作用面宽度，LH为该层土体厚度。

3.2 底板地基反力系数

贮液池底板以下的群桩基础同样以弹簧单元考虑，计算得到群桩基础的弹簧常数见表3，将群桩基础的弹簧常数除以底板面积得到底板弹簧的法线方向地基反力系数与切线方向地基反力系数

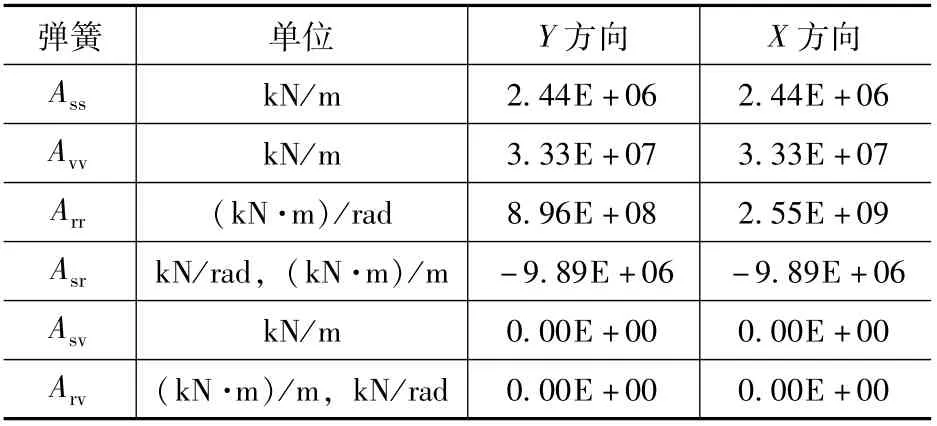
表3 群桩基础弹簧常数Tab.3 Spring constant of pile group foundation

群桩基础弹簧常数：

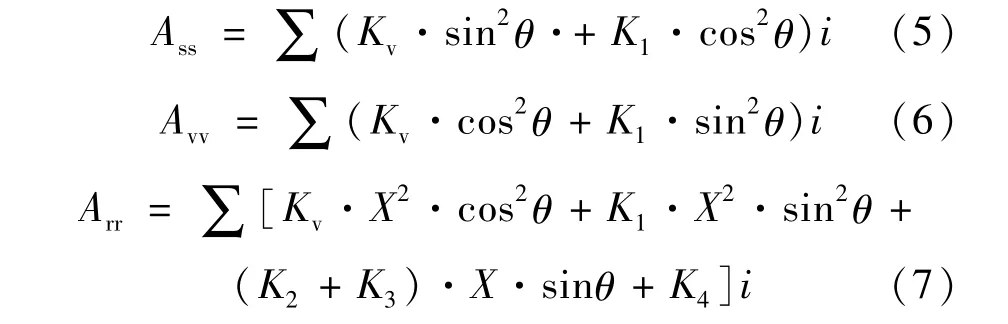
式中：i为单桩在x，y方向上第i根桩；Kvi为第i根桩的桩轴方向弹簧常数；K1i-K4i为柱轴直角方向弹簧常数；Xi为桩头的水平坐标；θi为桩轴垂直轴的角度；Ass为水平弹簧常数；Asr=Ars为水平与旋转连成弹簧常数；Arr为旋转弹簧常数；Asv=Avs为水平与垂直连成弹簧常数；Arv=Avr为垂直与旋转连成弹簧常数；Avv为垂直弹簧常数。

底板地基反力系数依据群桩基础的弹簧常数求得，将群桩法线与切线方向的弹簧常数除以矩形底板面积可得，法线方向地基反力系数kH为59731kN／m3，切线方向地基反力系数kV为4380kN／m3。

4 拟静力法

4.1 设计水平震度

本贮液池采用震度法［13］计算结构的地震响应。震度法是一种将对构筑物的地震作用力，根据构筑物的固有周期对应的响应加速度求出的设计水平震度，置换为静态荷载（惯性力、地震时土压、地震时动水压），求构筑物的地震时响应的抗震计算方法，设计水平震度计算公式如式（11）。

式中：a为结构在地震作用下的响应加速度，g为重力加速度。

本结构设计水平震度由式（12）、式（13）求出。

地上部设计水平震度Khf：

式中：Cz为地区修正系数，取1；SG为地基修正系数，取1.2；SI为重要度修正系数，取1.1；Kh0为标准设计水平震度，取0.2。

地下部设计水平震度Khb：

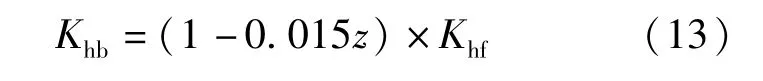
式中：z为埋深。

4.2 地下水动水压

贮液池处于地下水位以下的表面受到地下水压的作用，在地震时地下水动水压Pw的计算见式（14）。

式中：w0为水的单位体积质量，h为水深。

求出各单元受到的地下水动水压以面力施加在受力单元上，地下水动水压与基础各点标高的关系如图5所示。

4.3 内容水动水压

贮液池的内容水动压Pw1与地下水压以相同的方式施加在受力单元上，内容水动压Pw1的计算见式（15）。

式中：β为修正系数，当L／H=0.5时β取0.397，当L／H=4时，β取0.996，其余值由其线性内插求得，L为沿震动方向板的长度；H为总水深；h为单元重心距水面的距离。

4.4 动土压

动土压随深度变化如图6所示。

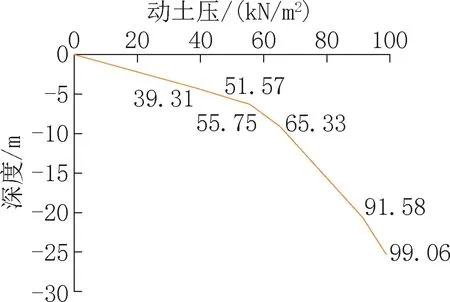
图6 动土压Fig.6 Dynamic earth pressure

地下水动水压、内容水动水压及静水压依照3.2节计算可得，地下土压计算公式如下：

静土压Ps：

动土压PEA：

式中：γ为土的单位体积质量；x为深度；Ks为静止土压系数，取0.5。

4.5 加载方式

将模型的四个外壁依照其法线方向分别将+X、-X、+Y、-Y四个外壁记作1、2、3、4号外壁。+X方向加震时，整个结构受到+X方向的惯性力；2号壁受到+X方向的力为：惯性力、地下水动水压、动土压、内容水动水压，-X方向受到的力为内容水静水压，+X与-X方向的力共同作用以面力施加于受力单元上；1号壁受到+X方向的力为惯性力、内容水静水压、内容水动水压，各个力相加后以面力施加于受力单元上。垂直于加震方向的内板受到内容水压时依照受力情况将内容水动水压、内容水静水压、惯性力组合以面力施加于受力单元上，铅垂方向施加结构自重；与地震动方向相同的单元受到静水压或静土压以相同的方式水平施加在各个单元上。

-X、+Y、-Y方向的最不利荷载组合同+X方向最不利荷载组合，这里不再赘述。

5 时程分析法

5.1 地震波的选取

进行时程分析时，地震波的合理选取是非常重要的一步，合理选择输入的地震加速度波是结构时程分析法实施的基础［14］。地震波的选取应满足地震动三要素的要求，包括：频谱特性、有效峰值和持续时间。频谱特性依照结构所处的场地类别和设计地震分组确定；有效峰值按照规范调整；有效持续时间一般不少于结构自振周期的5倍和15s，时间间隔按照需求设为0.01s或0.02s。

本文从地震波生成器SGSw中选取EL-Centro地震波，运用反应谱的概念来调整输入地震动加速度时程曲线，EL-Centro的时程曲线和加速度反应谱见图7，将EL-Centro波通过高速傅里叶变换使结构第一模态周期对应的反应谱加速度等于震度法下结构的设计水平地震度，使地震波可以合理地加载在本结构上，调整后的地震波及反应谱见图8。

图7 EL-Centro波地震加速度时程及反应谱Fig.7 EL-Centro wave seismic acceleration time history and response spectrum

图8 调整后的地震波加速度时程及反应谱Fig.8 Adjusted seismic wave acceleration time history and response spectrum

其中EL-Centro波的地震波加速度曲线峰值为0.2784g，对应的反应谱曲线峰值为2.4597g，调整后的地震波的加速度曲线峰值为0.0899g，对应的反应谱曲线峰值为0.7942g。结构设计水平震度最大值为0.264，由此对地震波进行调整，X方向的一阶模态周期为0.044s，Y方向的一阶模态周期0.051s，取结构第一模态周期为0.044s，由结构一阶模态周期调整后地震波反应谱对应的加速度为0.264g。

调整后地震波满足本结构在地震动三要素上的要求，可以施加在简化模型上进行时程分析。

5.2 时程分析法荷载组合

垂直于地震波方向并受到地下水压或内容水压的单元，其地下水动水压和内容水动水压按照以下公式计算作为附加质量与钢筋混凝土自重相加后以面力施加于受力单元的-Z方向，与施加地震波方向相同的单元不受动水压，但其垂直方向受到的静水压或静土压时以面力水平加载至受力单元上。

地下动水压作为附加质量：

内容动水压作为附加质量：

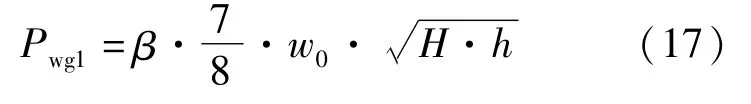
6 简化模型结果分析

分别对简化模型进行动力时程与震度法分析，以结构位移为例，+X方向加波时，在与+X方向垂直的外板沿高度Hx取6个节点；+Y方向加波时，在与+Y方向垂直的外板沿高度Hy取10个节点，沿宽度By取9个节点，Hx、Hy、By的位置见图3，得到震度法位移与时程分析法的节点最大位移，-X、-Y在Hx、Hy、By对称板的相同位置分别选取10个、9个、8个节点，这里不再赘述。

由图9所示，X方向加震时，两种方法节点位移的变化有着相似的趋势，+X方向加震时，高度未达到8900mm之前节点位移随着高度的增加而增大，高度达到8900mm之后节点位移随着高度的增加而减小；-X方向加震时，高度未达到12250mm之前节点位移随着高度的增加而增大，高度达到12250mm之后节点位移随着高度的增加而减小。

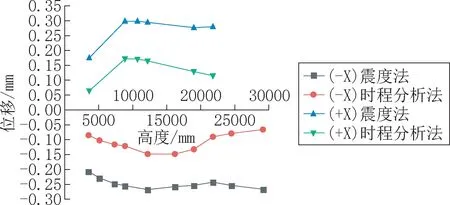
图9 X向加震外板节点沿Hx最大位移Fig.9 Maximum displacement of X-direction seismic external plate node along Hx

如图10所示，Y方向加波时两种方法计算得到的最大位移值在同一高度，+Y方向加震时，高度为7365mm时位移达到最大值，-Y方向加震时，位移最大处的高度同样为7365mm。

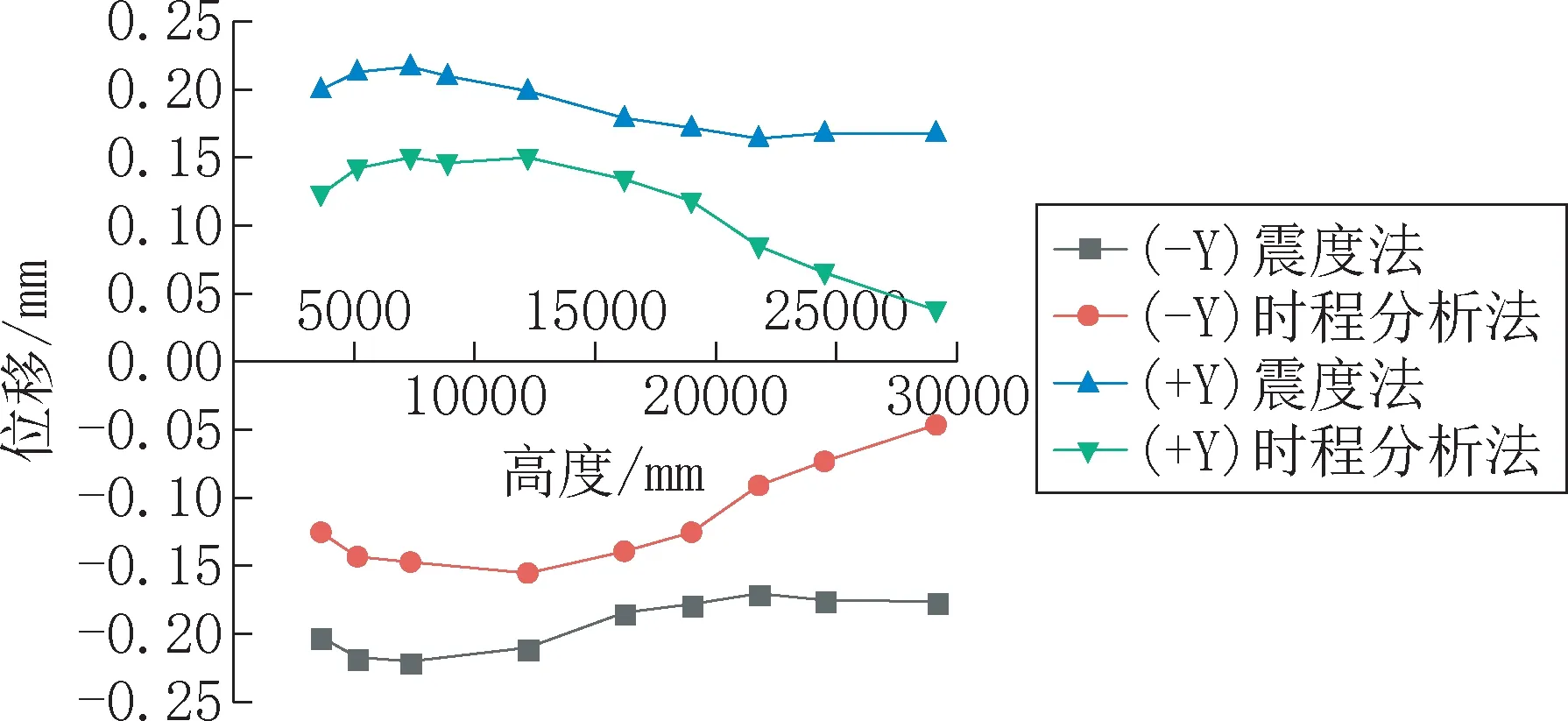
图10 Y向加震外板节点沿Hy最大位移Fig.10 Maximum displacement of joints of Y-direction seismic external plate along Hy

Y方向加震时，外板节点位移沿着By的变化如11图所示，+Y方向加震时，距原点距离小于14500mm时，两种方法的计算结果趋于平稳，此后随着距原点距离的增加而增大，位移最大值在距原点距离14500mm处，此后随着节点位移随着距原点距离的增加而减小；-Y方向加震时，节点位移在距原点距离17000mm时达到最大值，两种方法计算得到的节点位移的变化趋势相同。

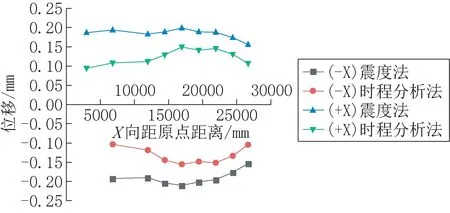
图11 Y向加震外板节点沿By宽度最大位移Fig.11 Maximum displacement along By the width of the outer plate under Y-direction vibration

由上述分析可得，震度法与时程分析法的位移最大值出现的位置相同，且震度法相对于时程分析法更为保守，结构需要进行时程分析时，利用静力法同样可以得到结构的最大变形或受力处。

由上述分析可以把结构的修正系数用结构拟静力法得到的最大应力或最大位移与时程分析法的到的最大应力或最大位移之比来表示，各项抗震指标的修正系数见表4。

表4 各项抗震指标的修正系数Tab.4 Safety factor of various seismic indexes

由表4可得：结构位移的修正系数较小，各项应力指标修正系数较大；各项修正系数中，-Y方向加震时结构的各项指标的修正系数相对于其余方向最小；取位移中-Y方向为结构的修正系数。拟静力法相对于动力时程分析法有着更安全的结果。出于安全性考虑，选取修正系数最小值1.37作为此结构的修正系数。

7 结构抗震分析

对本贮液池进行地震下的响应分析时，由于时程分析法计算复杂，工作量多，故采用拟静力震度法对结构进行抗震验算并用修正系数转换得到修正的拟静力法结果，该法得到的结构最大响应在数值上等于时程分析法最大响应值，采用此方法可以得到地震波下的结构最大响应。

分别对结构最小主应力、最大剪应力进行地震响应校核。钢筋混凝土结构最大剪应力出现在-X加波时的底板上，由5.1节修正系数取1.37，计算结果如表5所示。

表5 抗震验算结果Tab.5 Seismic verification results

由表5可得，拟静力震度法得到的结构最小主应力小于结构容许压应力，结构最大剪应力大于结构容许剪应力；由修正系数换算得到修正拟静力震度法的结构最小主应力与最大剪应力均小于结构允许值，因此鉴于拟静力法计算结果的保守性与经济性，以修正拟静力震度法的计算结果进行抗震性能验算，结构最大响应验算通过，不需要进行加固。

8 结论

本文对半地下贮液池结构的简化模型分别采用拟静力的震度法与时程分析法对原有结构进行抗震性能分析，提出针对该结构震度法相对于时程分析法的修正系数，由此对实际模型进行震度法的抗震性能验算并以修正系数辅助进行校核，得到如下结论：

（1）由拟静力法与时程分析法的计算结果得到的各项指标的修正系数易受结构与加震方向的影响，结构位移相对于压应力、剪切应力、Mises应力的修正系数更小；各方向的修正系数中，-Y方向加震时结构相对于其余方向最小，出于安全性考虑，以得到的修正系数最小值1.37作为此半地下水池结构的修正系数。

（2）本贮液池由拟静力法与时程分析法计算得到结构最大响应出现的位置相同，修正系数可以将拟静力法最大响应值转换为时程分析法的最大响应值，得到结构在地震波下的最大响应。