弯曲航道串列桥墩紊流宽度研究及应用
谭志荣 陈 彬 李青云 陈 维 林黎明
(武汉理工大学航运学院1) 武汉 430063) (内河航运技术湖北省重点实验室2) 武汉 430063)(交通运输部长江航务管理局3) 武汉 430010) (中国科学院力学研究所流固耦合系统力学重点实验室4) 北京 100190)
0 引 言
桥墩缩窄了航道宽度且产生阻水作用,改变了桥墩附近的水位、流速、水流挟沙力等[1].弯曲航道水流除纵向运动外,还会产生表流指向凹岸侧、底流指向凸岸侧的横向环流[2-4],严重影响船舶的航行安全.
在墩柱绕流紊动特性研究方面,Zdravkovich[5]对双圆柱体周围流场的研究表明:在(1.0 弯曲航道桥区水域作为船撞桥事故多发水域,由其带来的安全问题备受关注.如,桥墩周围流态复杂、船舶过桥操纵难度大和航行风险增加等.虽然文献[10]中规定建桥选址应该远离控制航道、弯道、分流口、汇流口,然而受限于当地经济、政策等限制,桥梁的选址规划不能完全按照有关标准,并且已建桥梁中存在个别桥梁通航净宽不足的问题,需要开展桥区水域水上交通安全隐患排查治理工作. 文中针对弯曲航道,参照桥区水流条件,采用SSTk-ω模型,借助流体计算软件Fluent进行二维数值模拟,通过比较不同工况下桥墩周围流向速度等值线图、速度流线图以及桥墩周围涡量场来分析得出桥墩紊流范围与墩柱直径,弯曲半径和来流速度的关系,拟合得出串列桥墩紊流宽度的计算公式,并以忠州长江大桥为例进行实证分析. 建立图1的经典圆柱(其直径为D)绕流计算模型,其中均匀自由来流(其速度为U∞)由左至右绕过柱体;并且建立图1的直角坐标系(x,y),其中x轴沿着流动方向,y轴则是与来流方向垂直,同时坐标原点放置于柱体对称中心. 图1 圆柱绕流及其计算区域示意图 流体的运动都符合质量、动量及能量守恒三大定律.在当前研究条件下,河水密度ρ保持不变,且重力仅作用于深度方向,假设温度保持常数;在桥区流场研究中,流场水平尺度一般远大于垂向尺度,研究圆柱形桥墩紊流范围问题可用二维数值模拟方法来研究[11-13];因此在当前二维流动条件下,建立如下的二维不可压缩连续性方程与N-S方程. 质量守恒方程: (1) 动量守恒方程: (2) 式中:▽为梯度算子;u为速度矢量,其包括两个速度分量u和v;p为压力;μ为流体动力黏度系数. 除了上述流速和压力之外,桥墩尾迹区中还特别关注的一个典型物理量是涡量,定义为速度矢量的旋度,即Ω=×u;特别地,在当前研究问题中,只有深度方向的涡量存在,即 采用DES(离散涡模拟)湍流模型中的剪切应力输运(shear-stress transport,SST)k-ω模型,其中:k为湍动能(turbulence kinetic energy),ω为比耗散率(specific dissipation rate);该模型与标准的k-ω模型相比较,考虑了剪切应力的波动传播,更加准确可靠. (3) (4) 式中:Gω为ω的产生项;Gk为由于平均速度梯度导致的湍动能产生项;Γk,Γω为k与ω的有效扩散项;Dω为正交发散项;Sk与Sω为自定义参数. 有效扩散项方程: (5) (6) 式中:σk与σω为k与ω的湍流普朗特数;μt为湍流粘度系数. 数值模拟的结果与湍流模型的选取、计算域的尺度,以及网格密度有关,然而目前针对流体的数值模拟研究中,没有一个固定的划分依据,因此需要开展无关性检验来验证数值模拟结果的准确性.为了验证模型计算结果与所选取计算域的尺度,以及网格的划分密度无关,以无界流动区域内单圆柱形桥墩绕流为例,选取若干尺度考察计算域及网格密度对数值模拟结果的影响,结果见图2和表1. 由表1可知,在本文所选取的的计算域尺度和网格密度对数值模拟的计算结果影响较小,可以用于弯曲航道桥区的流场分析. 为研究弯曲航道桥区流场分布状态,考虑到实际当中弯曲航道水域范围,同时由于L/D=2时相对紊流宽度最大[14],因此本文计算域边界为航道宽度400 m,桥墩放置在航道中心线处,通航孔间距设置为240 m.以航道宽度400 m、弯曲半径R为800 m、串列双墩的单个桥墩直径D为10 m、桥墩间距为L=2D、流速V为1 m/s的工况为基础算例,以此来研究在不同弯曲半径、不同流速、不同桥墩半径条件下,桥墩布设对流场的影响.设计R为850,900,950和1 000 m;V为1.5,2,2.5和3 m/s、D为5,15 m作为对比工况.工况设置见表2,计算域及边界条件示意图见图3,基础算例流向速度等值线图见图4. 表2 模拟工况设置表 图3 计算区域及边界条件 图4 基础算例速度等值线图 以R为单一变量,D为10 m,V为1 m/s,对R分别为850,900,950和1 000 m进行数值模拟,见图5. 图5 不同弯曲半径速度等值线图 由图5可知:随着航道弯曲半径增大,即曲率减小,中高速流动区域逐渐向凸岸扩展,这是由于水平面内的离心力逐渐削弱,导致具有向凹岸一侧流动趋势的流速逐渐减缓,从而增大了凸岸一侧的流速;即使如此,凹岸一侧桥墩的平均来流速度仍然总体高于凸岸一侧桥墩的平均来流速度;正是上述流速分布特征,导致高速凹岸一侧桥墩尾迹中流速脉动范围显著收窄;而低速凸岸一侧桥墩尾迹中流速脉动范围则相对扩大,且随着航道弯曲半径增大,而逐渐收窄. 以D为单一变量,V为1 m/s,R为800 m,对D分别为5,15 m时进行数值模拟,见图6. 图6 不同桥墩直径速度等值线图 由图6可知:高速流动区域与低速流动区域分布没有明显改变,但随着桥墩直径增大,桥墩的阻水宽度增大,从而同时增大了两侧桥墩的流速脉动范围;随着桥墩直径增大,两侧桥墩中间不受脉动的范围减小,对于水面航行船舶而言,适航水域范围减小;同样的凸岸一侧桥墩尾迹中的漩涡脱落及其波动显著较凹岸一侧桥墩尾迹中的强烈,并且向下游延伸的范围变大,表明随着桥墩直径的增大向下游影响范围也将更广,对船舶正常航行产生的影响也就越久. 设置V为单一变量,D为10 m,R为800 m,对V分别为1.5,2,2.5和3 m/s进行数值模拟,见图7. 图7 不同来流速度等值线图 由图7可知,随着来流速度增大,整体流动区域趋向于高速流动,增大了两侧桥墩的流速脉动范围;双桥墩中不受脉动影响的范围增加,但不如增加桥墩直径增加明显;增加来流速度,延伸下游区域明显增加,桥墩下游较远处流态依然比较复杂. 桥墩紊流是一种非常复杂的水流运动形式,桥墩两侧的流线较其他地方密集,流速更大,在桥墩尾部出现紊流[15],桥墩紊流区存在“墩吸流”,船舶在桥区航行时容易受到紊流区水流的影响,容易发生船桥碰撞事故.表3为不同工况紊流宽度汇总表. 表3 不同工况紊流宽度汇总表 通过拟合表3中的数据,得到弯曲航道圆形桥墩凸岸侧与凹岸侧最大紊流宽度表达式: (7) (8) 式中:Bq1,Bq2分别为凹岸侧和凸岸侧桥墩紊流宽度. 忠州长江大桥位于长江上游忠县水道的弯曲航道(长江上游航道里程约为428.8 km),跨径组合为205 m+460 m+205 m,桥面宽26.5 m.该航道位于三峡库区回水变动区,航路航法为上、下行船舶各自靠右航行,大桥上游右岸存在浅滩,汛期时流态复杂. 主航道布置在10#及11#桥墩之间,主桥墩宽度约为12 m,流速选为3.5 m/s,弯曲半径约为1 000 m,墩柱附近水深取25 m.利用本研究弯曲航道紊流宽度式(7)~式(8),计算得出凹岸与凸岸侧紊流宽度分别为32,45 m,大于文献[16]中的计算结果29.8 m,这是因为弯曲航道的紊流宽度相较于顺直航道紊流宽度有所增加. 1)文中采用SSTk-ω模型,借助流体计算软件Fluent进行二维模拟,对比分析航道弯曲半径、来流速度以及桥墩直径对桥墩紊流宽度的影响,进而总结出圆柱形桥墩紊流宽度计算公式. 2)弯曲航道凸岸侧桥墩紊流宽度大于凹岸侧桥墩紊流宽度,同时凸岸一侧流场相较于凹岸一侧长度更长,随着航道弯曲半径的增加,桥墩紊流宽度有所减小;相同条件下,随着来流速度以及桥墩直径的增大,紊流宽度有所增加. 3)依据数值模拟结果分别拟合得出串列圆形桥墩凸岸侧与凹岸侧的紊流宽度计算公式,选取长江上游典型弯曲河段的工程实例验证了改进后的紊流宽度的准确性,可为后续弯曲航道桥梁通航宽度确定提供理论支持. 4)实际上桥墩紊流应该是复杂的三维流场,但是受限于流场的复杂性和研究时间等因素的限制,仅选择圆形串列桥墩进行二维紊流计算研究.后续研究中为更全面地研究桥区三维紊流特性,可进行三维流场模拟仿真以及选择更多的墩形(如方形、水滴形等)做更进一步的研究.1 弯曲航道水流模拟
1.1 研究对象
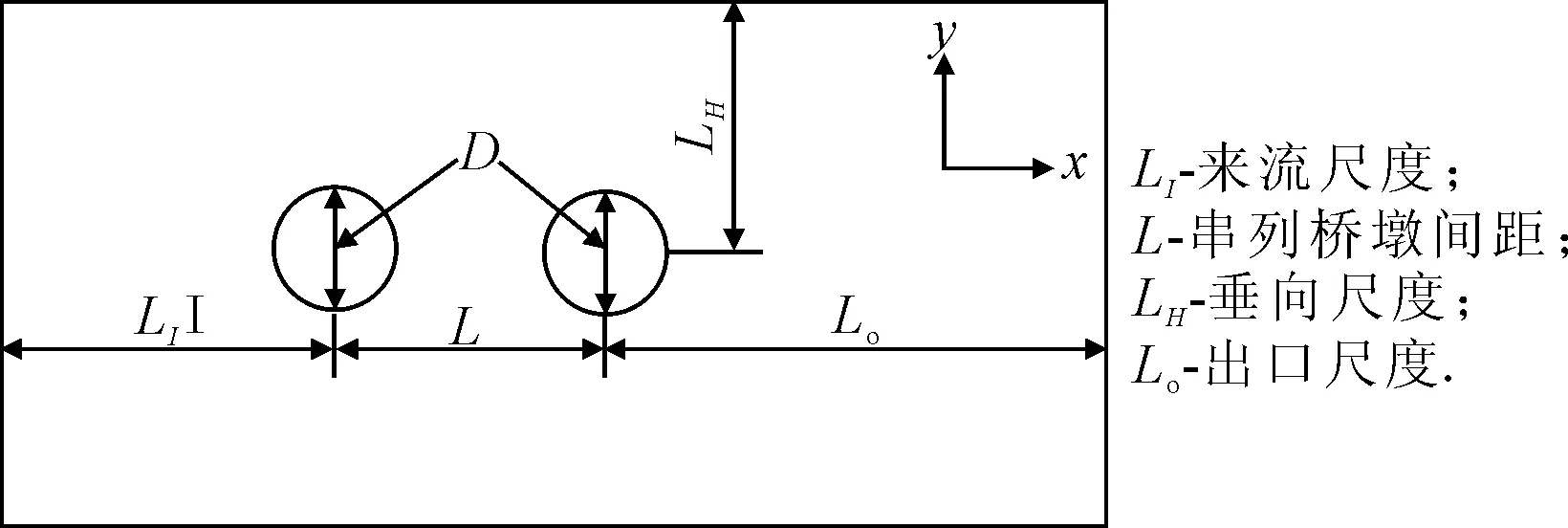
1.2 控制方程
1.3 湍流模型
1.4 无关性检验
2 模拟结果对比与分析

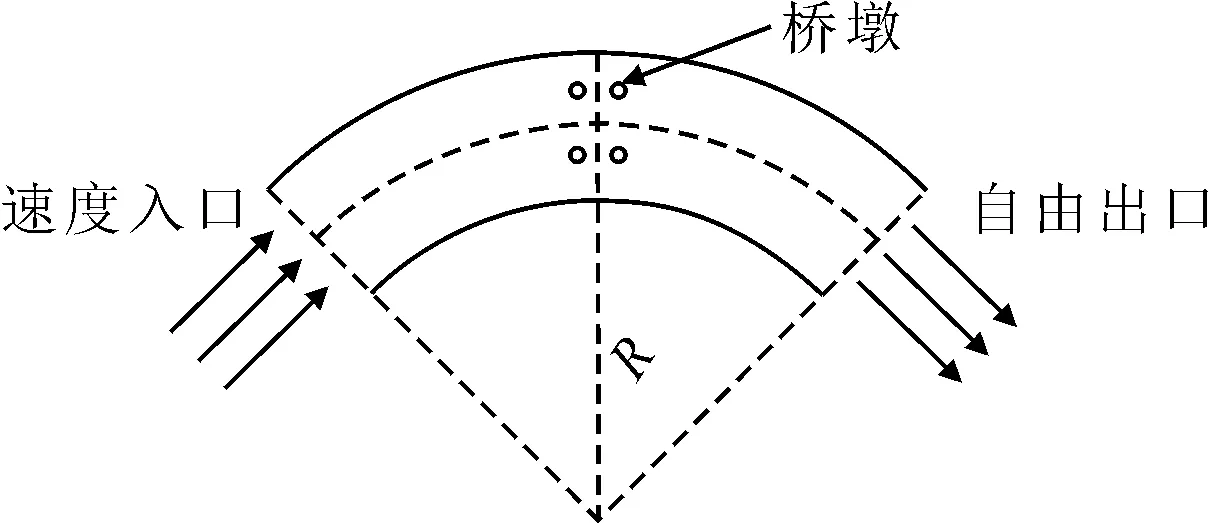
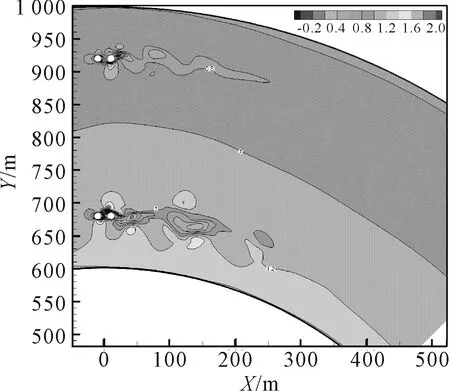
2.1 航道弯曲半径的影响
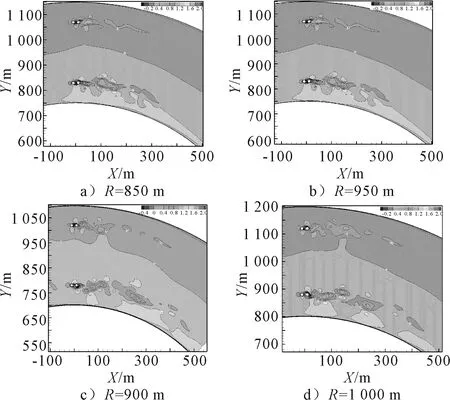
2.2 航道墩型尺寸的影响

2.3 流速的影响

3 紊流宽度经验公式及应用
3.1 紊流宽度经验公式

3.2 工程实例验证
4 结 论

