基于Maxwell方程的沥青混合料介电模型研究

陈雍春 杨川文 于晓贺

(上海市政工程设计研究总院(集团)有限公司1) 上海 200092) (武汉理工大学交通与物流工程学院2) 武汉 430063)

0 引 言

沥青路面的无损检测主要依赖于沥青路面各结构层的相对介电常数差异来实现[1-2].而作为多相复合材料，沥青路面的相对介电常数是由其内部各单一材料的相对介电常数所共同决定的.在现有的研究中，一般采用复合介电模型来描述多相复合材料各组成材料的相对介电常数与其在总材料组分所占比例之间的关系[3].沥青混合料作为典型的复合材料，其介电模型中主要包含沥青、集料和空气三种物质.沥青混合料的介电模型是研究沥青混合料的介电特性的基础，也是实现沥青路面无损检测的理论依据，可以将其与部分沥青路面的实际检测指标的计算方法结合，建立起沥青混合料介电模型与密度、压实度、沥青含量等实际检测指标的理论关系，为实现工程指标检测的无损化发展提供理论依据[4-5].

适用于沥青混合料的复合材料介电模型目前较少，应用较为广泛的模型大多来自地质勘探、石油勘探等领域，如Brown模型、CRIM模型和Rayleigh模型等，但这些复合材料介电模型对沥青混合料的适用性并未得到进一步验证[6].现有的复合材料介电模型在沥青混合料领域并未取得理论上的突破，所采用的理论模型也大多是借鉴其他领域的应用[7-8].因此，开展对沥青混合料介电模型的理论研究有利于更好地描述沥青混合料各组成材料与其在总材料组分所占比例之间的联系，以实现对沥青路面工程指标的无损检测.

文中基于Maxwell方程，通过理论推导得到了适用于沥青混合料的复合材料介电模型，采用介电网络分析仪测定了两组沥青混合料在多个频率下的相对介电常数，并依据测量结果与Brown模型、CRIM模型和Rayleigh模型进行精度对比验证其优越性.

1 理论模型

电磁波依照Maxwell方程的基本规律在沥青路面中传播时，由于不同结构层或异常病害区域的介电特性存在差异，则电磁波会在沥青路面各结构层交界面和异常病害区域处发生传播突变，可以依据得到的突变电磁波信号判断沥青路面的厚度和异常区域位置[9].

对于沥青混合料而言，Brown模型、CRIM模型和Rayleigh模型的表达式为

(1)

(2)

(3)

式中：Vi为沥青混合料中各组份材料所占体积比例；εi为各组份材料的相对介电常数.

研究中可以认为沥青、空气是各向同性的材料，但集料由于其结构的复杂性，可以认为是各向异性材料.各向同性材料的平均电场为[10]

D=εE

(4)

式中：D为电位移矢量；E为电场强度，E可表示为式(5)，ε可表示式(6)

E=E+δE

(5)

ε=ε+δε

(6)

式中：δε为电场强度中某点位置处的变化值.

2.电力自动化技术按照内容可分为调度、发电厂以及变电站自动化三部分，主要技术要求包括：电网调度中电力终端电网信息的采集与分析，通信网络中的信息传输以及整理预测；发电厂自动化中机械自动控制系统、发电量控制系统以及电压控制系统等的自动化控制；变电站综合自动化中变电站相关设备的重新组合优化综合运用信息、电子、计算机等技术，实现对整个电力系统设备、线路等的实时监控、测量、保护与历史存档等功能；配电网自动化则主要实现配电网调度系统、馈线系统、用电管理系统等的自动化管理，完成电网信息数据采集监控、故障预测与故障恢复等自动化功能。

由此可得：

D=(ε+δε)(E+δE)

(7)

D=εE+δεδE

(8)

式中：δE=0，δε=0.

为求δεδE，可结合方程·D=0，化简后公式可得

(9)

联立式(5)则可得

·δE=-E·lnλε

(10)

以E和δE=-δU分别代替式(10)，其中U为电位函数，可近似得

2δU=E·lnε

(11)

对式(11)两端求梯度得

2δE=(E·)lnε

(12)

(13)

对式(13)乘以δε进行化简，并求得各材料的平均值后与式(8)联立，可得：

(14)

与式(4)对比可知

(15)

(16)

结合适用性较好的CRIM模型，结合式(16)，则沥青、空气组成的各向同性材料的介电模型可以表示为

Va(εa-ε)lnεa]

(17)

式中：εas+a为沥青、空气的复合相对介电常数；vas为沥青材料的体积比例；Va为空气材料的体积比例；εas为沥青材料的相对介电常数；εa为空气材料的相对介电常数.

故可得沥青混合料的相对介电常数为

ε=

(18)

2 试验设计

2.1 试验设备

介电网络分析仪可以在多个频率范围下测量待测材料的相对介电常数和介电损耗值，见图1.

图1 介电网络分析仪

2.2 试验材料

选取湖北某地的玄武岩、石灰岩两种集料，SBS改性沥青作为沥青材料，经过试验验证，文中所用材料均能满足沥青路面试验规范的各项性能需求.采用两种沥青混合料级配见图2，其中对玄武岩和石灰岩沥青混合料，采用的最佳油石比为5.6%，针对石灰岩沥青混合料，采用的最佳油石比为4.3%.

图2 AC-13C 和AC-20C合成级配曲线图

试验采用旋转压实仪压实成型，得到的直径和厚度分别为15、17 cm的标准原始试件，见图3a)，再利用钻芯机和切割机将试件加工成直径和高度分别为10、17 cm的试件，见图3b).由于介电网络分析仪测量装置的尺寸限制，将所得标准试件加工成厚度为1.5 cm的薄片，进一步采用钻芯机钻芯得到直径为3 cm的测试试件，试件的准备过程见图3.每组采用五个试验样品，将两组样品编号为1-1～1-5和2-1～2-5.

图3 试验样品加工过程

2.3 试验方案

使用介电网络分析仪在室温条件下进行测量，测量两类沥青混合料试件在100 Hz～1 MHz频率的相对介电常数，并绘制频率与相对介电常数的关系见图4.

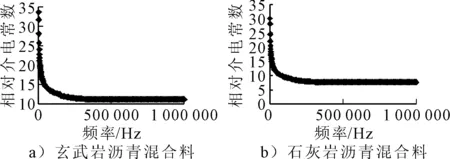
图4 沥青混合料相对介电常数随频率变化图

由图4可知，频率是影响沥青混合料介电常数的主要因素，两种沥青混合料的相对介电常数均会随着频率的变大而减小.当频率变大至1 MHz左右，沥青混合料的相对介电常数即不再会产生变化，保持恒定.故将各组沥青混合料在试验频率为1 MHz下的相对介电常数来进行对比验证模型的适用性.同时测定玄武岩和石灰岩集料的相对介电常数为11.2和7.8，SBS改性沥青的相对介电常数为2.4.

3 试验结果分析

测量两类沥青混合料的空隙率，并记录在1 MHz下的相对介电常数，见表1.

表1 各组空隙率与相对介电常数数据

依据表1的相对介电常数试验结果，绘制各理论模型的相对介电常数计算数据(见图6)，同时计算文中各理论模型的平均相对误差，见图5～6.

图5 各模型精度对比分析图

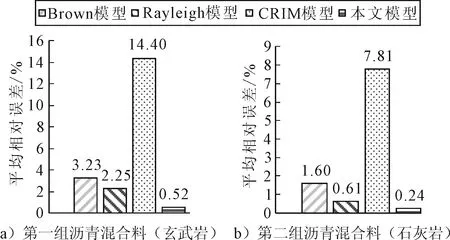
图6 各介电模型平均相对误差对比图

由图5～6可知，Brown模型、CRIM模型、CRIM模型和Rayleigh模型针对玄武岩沥青混合料的各组平均相对误差差别较大，仅有本文模型的平均相对误差在1%以下，其他介电模型的平均相对误差均在2%以上，Rayleigh模型的平均相对误差更是超过了10%.针对石灰岩沥青混合料，本文模型和CRIM模型均有较好的计算精度，平均相对误差均在1%以下，但本文模型的平均相对误差更小，具有更高的可行性.由此可知，本文模型对于两类沥青混合料而言均具有最小的平均相对误差，可以作为沥青混合料介电特性研究的基础.而现有的其他模型中，CRIM模型精度最高，Brow模型次之，Rayleigh模型精度最低，这与其适用领域并非在沥青混合料领域有关，导致其存在着一定的误差[11-12].

4 结 论

1)频率是影响沥青混合料相对介电常数的主要因素，其会随着频率的变大而减小，在频率增大到1 MHz左右不再发生明显变化.这说明在1 MHz左右沥青混合料才会充分极化，具有较为稳定的介电特性，为无损检测的频率选取提供了依据.

2)文中推导得到的新介电模型拟合精度较高，两种沥青混合料的平均相对误差仅为0.5%，优于其他几类现有模型.