坐标变换法描述主应力空间中π 平面上的应力偏量1)
王秀锋 赵颖涛
∗(湘潭大学材料科学与工程学院,湖南湘潭 411105)
†(北京理工大学宇航学院,北京 100081)
主应力空间中π平面上应力偏量的描述是屈服准则和塑性本构关系的基础,是弹塑性力学课程的重要内容。常见教材中π平面上应力偏量的描述都是基于空间中向量的几何关系,即先在三维坐标上取单位长度,将其投影到π平面上。根据它们在π平面上的坐标表达式,来描述主应力空间中任意一点应力的偏量部分[1-3]。该推导过程繁锁,特别是在求解其逆表达形式时,需设一组变量作为三维应力分量,通过建立方程组来求得。事实上,主应力空间中的任何一点应力状态矢都可分解为π平面内两个偏量和沿着其法向方向的应力,它们对应的三个方向刚好构成了一个正交坐标系。根据弹性力学里的不同笛卡儿坐标系中矢量的分量转换关系,即转轴公式[2],就能轻松导出上述两个坐标系(即应力空间中的主坐标和π平面及其法向坐标系) 之间的关系,从而得到任意应力在π平面上的应力偏量描述。
1 主应力空间及π 平面
任意一点应力状态,可以通过参考坐标系下应力张量来描述,也可以用三个主应力和主方向来描述。由三个主应力分量σ1,σ2,σ3为坐标轴组成的空间直角坐标系称为主应力空间。设主应力空间沿主方向的3 个基矢记为(e1,e2,e3),其中任意一点应力(对应图1 中的OP) 的应力状态矢可表示为[1-3]
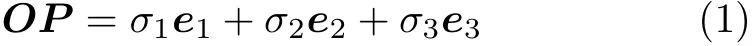
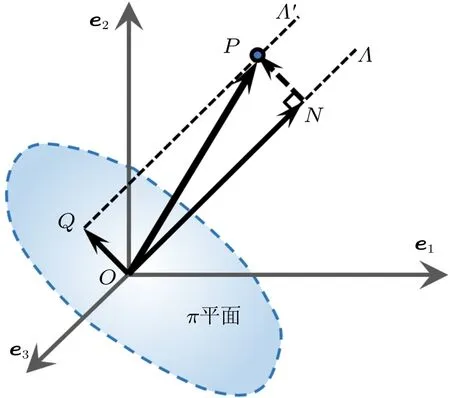
图1 主应力空间中一点应力矢及其在π 平面上的投影
设ON为主应力空间的等倾线(又称Λ线),过原点且法向为ON的平面是主应力空间的等倾面,称之为π平面。其方程为

其中σm= (σ1+σ2+σ3)/3,为平均正应力,si=σi-σm(i=1,2,3),si为应力偏量的三个主值。显然
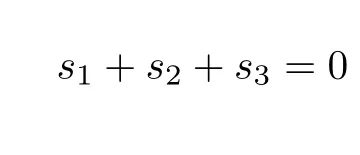
也即OQ必然在π平面内。
由于静水应力对材料的塑性变形没有影响,因此研究材料的塑性变形时,通常只需要分析应力偏量部分,即度量任一点应力在二维π平面上所对应的偏量部分的大小和方向,建立三维主应力空间和二维π平面之间的数学关系。
常见教材中π平面上应力偏量的描述都是基于空间中向量的几何关系,过程繁琐容易出错。本文将利用坐标变换的方法,即根据任意矢量的分量在不同坐标系下的转换关系,轻松得到主应力空间中的任意应力分量与π平面上应力偏量的对应关系。
2 应力分量从主坐标系变换到π 平面坐标系,即(e1,e2,e3) →(,,)

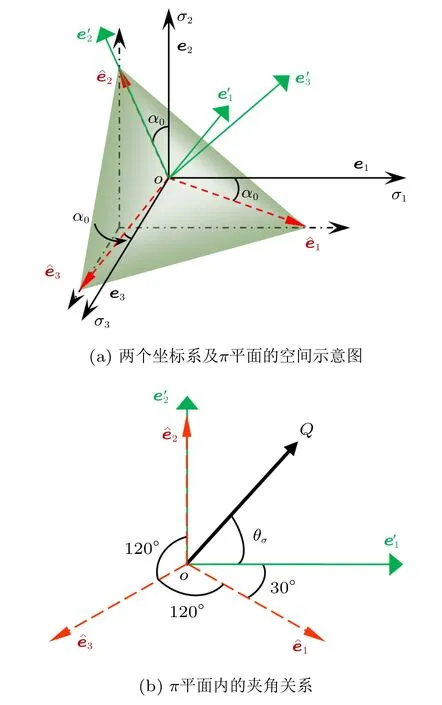
图2 两个坐标系间的几何关系
由坐标系间的夹角余弦值[4],新旧坐标系下的转换系数矩阵βij可写为
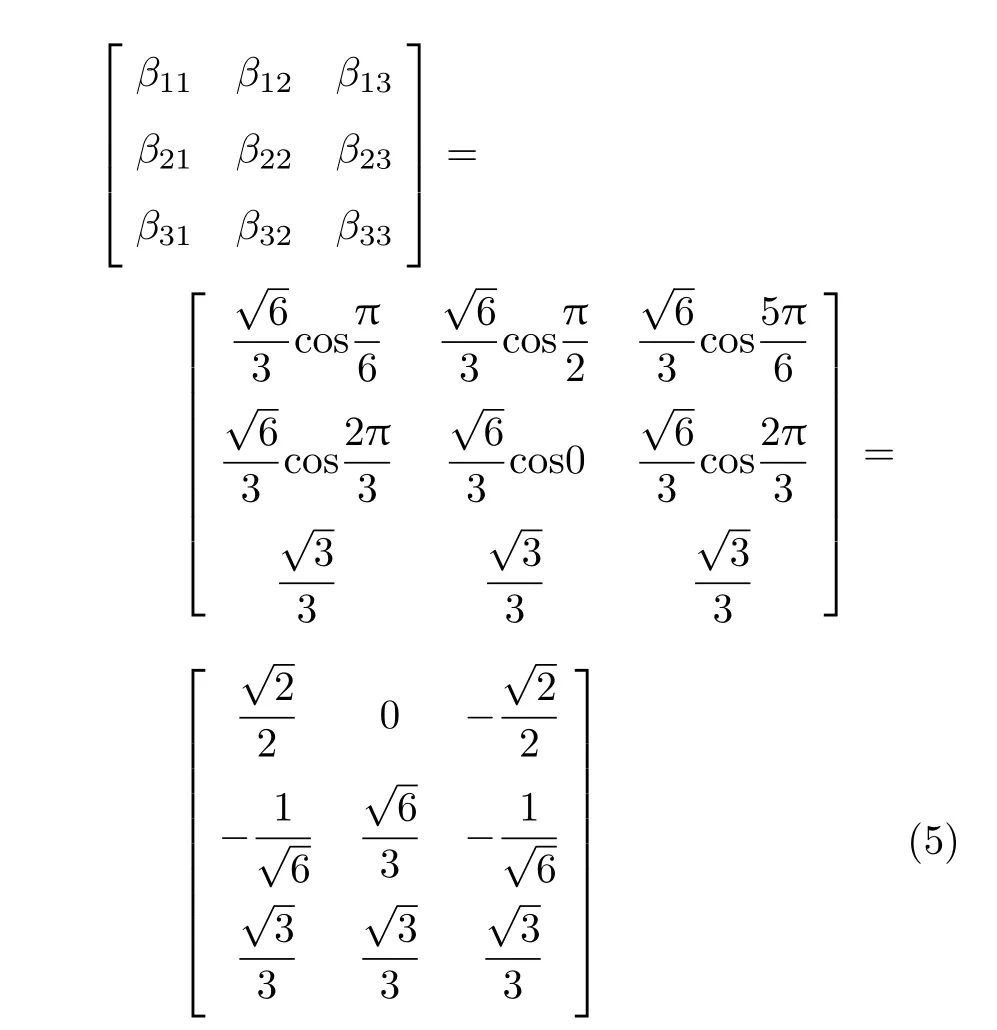
代入式(4),可得应力状态矢在π平面坐标系下的分量(σ′1,σ′2,σ′3)
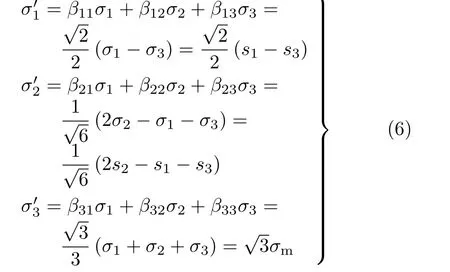

3 应力分量从(主坐标系)到π平面坐标系的逆变换,即,,→(e1,e2,e3)

对应的偏量部分可以表示为
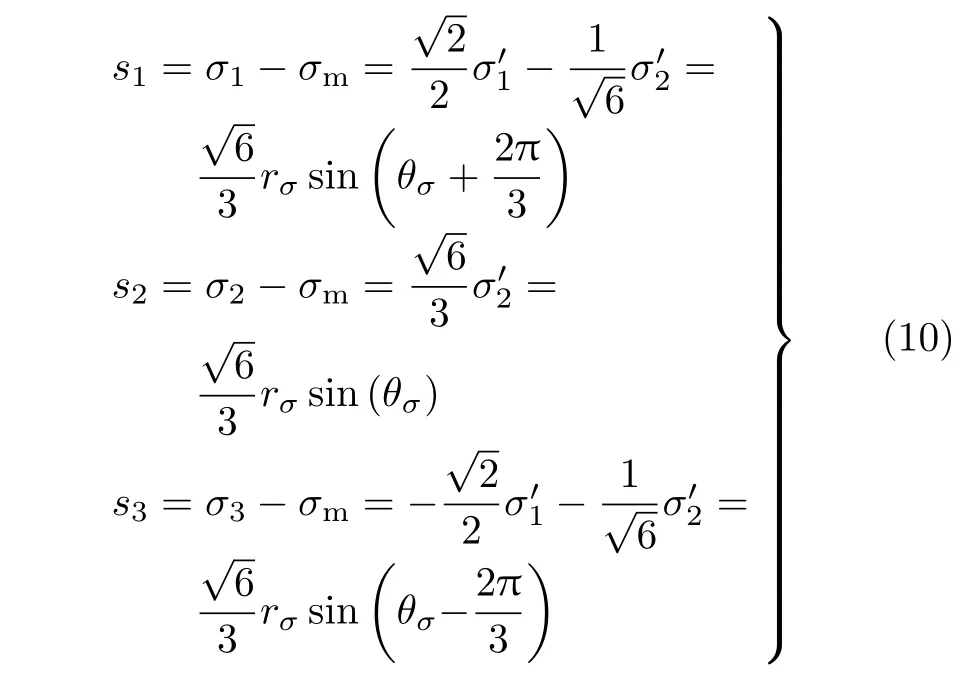
上述推导得到了与现有教材完全一致的应力分量关系,但数学思路更为清晰,可以作为该知识点的一个教学补充。
4 结论
本文利用π平面及其法向构造了新的π平面坐标系,并基于坐标变换方法,通过应力空间中主坐标系和π平面坐标系之间的坐标变换关系,得到任意应力在π平面上的应力偏量描述。与传统的几何投影法相比,本方法更为方便简洁,与传统方法又有异曲同工之处,在弹塑性力学的教学中可以对比使用。

