考虑拉压不同模量压力隧洞应力和位移弹性解1)

赵增辉 洪娟霞 刘 浩 李灿林

∗(山东科技大学能源与矿业工程学院，山东青岛 266590)

†(矿业工程国家级实验教学示范中心(山东科技大学)，山东青岛 266590)

压力隧洞是埋藏于地层具备一定功能的地下硐室结构，如油气管道、供水系统、城市地下交通等。硐室开挖后，一般采用衬砌结构进行支护，因此地层压力和硐室内压由衬砌和围岩共同承担。长期以来，研究人员在压力隧洞的应力、位移弹塑性解答，以及围岩抗力系数等方面取得了大量成果[1-4]。然而，岩石和混凝土是典型的非均匀材料，其拉伸和压缩弹性模量并不相同，一般情况下，拉伸模量小于压缩模量。因此不考虑模量差异所得到的理论解无法真实反映材料的力学行为。

1864 年，Saint-Venant 首次提出了双模量材料概念。1941 年，Timoshenko[5]在研究纯弯曲梁的弯曲应力时，也提出同样的概念。20 世纪80 年代，阿姆巴尔楚米扬[6]建立了不同模量理论。自此，国内人员对该理论掀起了研究热潮：倪国荣等[7]分析了不同模量理论在岩石地下工程中的应用；杨钊等[8-9]分析了围岩不同模量特性对隧洞支护结构的影响以及对巷道应力和变形的影响；Zhao 等[10]考虑到岩石的不同模量特性，推导出深圆孔围岩位移计算公式，并与等模量下的计算结果进行比较，发现拉压不同模量特性对围岩位移结果有影响。有关的数值计算结果表明[11-13]，若沿用相同模量弹性理论或有限元对有关问题进行计算，其结果将与采用不同模量模型材料所得的刚度和强度有较大的偏差。因此，考虑地层和衬砌在不同受力状态下的模量差异，建立考虑拉压模量不同时压力隧洞的应力及位移解，对硐室和支护结构设计具有重要理论和工程意义。

1 考虑拉压不同模量压力隧洞弹性新解

1.1 拉压不同模量弹性物理方程

假设材料在拉伸时的弹性模量和泊松比分别为E+和µ+，受压时的弹性模量和泊松比分别为E−和µ−，在单向应力状态下，材料的应力-应变(σ-ε)关系可简化为如图1 所示的双直线模型。

图1 不同模量材料的本构关系Fig.1 Constitutive relationship of materials with different modulus

在柱坐标系下，三向应力状态主应力和主应变的关系可表示为[8]

式中，er，eθ，ez为主应变，σr，σθ，σz为主应力，aik(i,k=1,2,3)为弹性常数，也称柔度系数。根据主应力符号的不同，柔度系数aik的取值如表1 所示。

表1 考虑拉压不同模量时物理方程系数取值Table 1 Values of physical equation coefficients considering different modulus of tension and compression

1.2 压力隧洞分析模型

1.3 考虑拉压模量不同时应力和位移的弹性统一解

该问题为轴对称问题，故衬砌和地层中切向应力τrθ= 0，切向位移uθ= 0，所有应力和位移分量仅是r的函数，忽略体力影响，平衡微分方程为

图2 压力隧洞简化模型Fig.2 Simplified model of pressure tunnel

1.4 考虑拉压模量不等时衬砌和地层的弹性解

以角标L 和R 区分式(9) 和式(10) 中衬砌和地层的解答，利用边界条件(σrL)r=a=-q，可得

2 结果分析与讨论

2.1 考虑模量差异弹性解的退化

若不考虑衬砌和地层拉压弹性模量差异，即认为

式(23) 和式(24) 即为弹性力学关于压力隧洞的经典解答。

2.2 拉压弹性模量不同时压力隧洞应力及位移的分布规律

取表2 所列参数分析，工况一为不考虑模量差异，工况二和三考虑模量差异，设隧洞半径为a=3 m，衬砌外径b= 3.4 m。设衬砌和围岩的压拉弹性模量比分别为λ1和λ2，压拉泊松比分别为η1和η2。

表2 分析参数Table 2 Analysis parameters

图3(a) 所示为应力经典解答与新解对比，下标o 代表经典解，n 代表拉压模量不同时新解。可见，从内部衬砌到外部地层，径向应力新解的应力值始终大于经典解，而切向应力的新解要小于经典解。相比较而言，模量差异对衬砌切向应力影响更显著。图3(b) 所示为压力隧洞位移经典解与新解的对比，拉压模量差异对压力隧洞位移的影响较大。自硐室内壁向无穷远处位移值逐渐减小，隧洞位移经典解小于新解的值。

图3 压力隧洞经典解与新解对比Fig.3 Comparison between classical solution and new solution of pressure tunnel

为进一步分析压拉模量差异对隧洞力学行为的影响规律，图4 绘制了λ2= 1，λ1取不同值时压力隧洞的应力及位移对比图。当内部衬砌压拉弹性模量比不同时，仅对衬砌中的切向应力产生明显的影响，λ1越大，切向应力值越小，λ1对径向应力及外部围岩的切向应力影响不大。λ1对衬砌和外部围岩位移具有显著影响，λ1越大时，压力隧洞位移值也越大。

图4 衬砌模量差异对压力隧洞应力和位移分布影响Fig.4 Influence of lining modulus difference on stress and displacement distribution of pressure tunnel

图5 为λ1=1，而λ2取不同值时压力隧洞的应力及位移对比图。围岩压拉弹性模量差异对压力隧洞切向应力和位移都会产生较大的影响。从图5(a)来看，压拉弹性模量比λ2越大，切向应力值越小，λ2对径向应力值产生的影响较小。由图5(b)，压拉弹性模量比λ2越大，衬砌位移越小。λ2对地层位移影响较复杂，随压拉弹性模量比增大，围岩位移越平缓，衰减越慢。

图5 围岩模量差异对压力隧洞应力和位移分布影响Fig.5 Influence of surrounding rock modulus difference on stress and displacement distribution of pressure tunnel

此外，围岩和衬砌压拉泊松比差异对压力隧洞应力及位移影响都很小，可以忽略不计，限于篇幅，不再赘述。

2.3 拉压模量差异对围岩弹性抗力系数的影响

围岩抗力系数是表征围岩抵抗衬砌向围岩方向变形能力的指标，衬砌和围岩取相同的压拉模量比，图6 给出了利用式(21)得到的压拉模量不同时的围岩弹性抗力变化曲线。从图中可以看出，随着压拉模量比逐渐增大，围岩弹性抗力变化呈抛物线形，变化幅度较大，压拉弹性模量比在1.6 附近达到最小值。由此可知，压拉模量不同对于围岩弹性抗力系数也会产生较大影响。

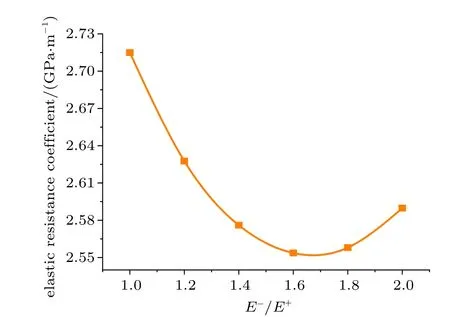
图6 压拉模量比不同时的围岩弹性抗力系数Fig.6 Elastic resistance coefficient of surrounding rock with different compression-tensile modulus ratio

3 结论

考虑围岩和衬砌拉压弹性常数差异，对弹性力学中关于压力隧洞的应力和位移解答进行了重新推演，并分析了拉压弹性常数比对解答的影响，主要结论如下。

(1)从内部衬砌到外部地层，径向应力新解始终大于经典解，而切向应力的新解要小于经典解。相比较而言，模量差异对衬砌切向应力及压力隧洞位移的影响比较显著。随着距内壁距离增大，位移值逐渐减小，隧洞位移经典解小于新解的值。

(2)衬砌压拉弹性模量比仅对衬砌中的切向应力产生明显的影响，对径向应力及外部围岩的切向应力影响不大，围岩压拉弹性模量差异对压力隧洞切向应力和位移都会产生较大的影响。压拉泊松比差异对压力隧洞应力及位移影响都很小。

(3)随着压拉模量比逐渐增大，围岩弹性抗力变化呈抛物线形，变化幅度较大，压拉弹性模量比在1.6 附近达到最小值。