基于最优加权组合模型的建筑安全事故预测

孔凡文，张晴晴

(沈阳建筑大学管理学院，辽宁 沈阳 110168)

近年来，建筑业一直是我国的重要支柱产业之一，在GDP中所占的比重由2010年的6.61%增长至2019年的7.16%，成为拉动GDP增长的主要动力之一。加强施工现场的安全管理对于促进建筑业的发展具有重要意义，而事故预测是安全管理的重要内容，建立精确的事故预测模型能有效提高安全管理水平。

在建筑安全事故预测方面，常用的预测方法有单项预测方法和组合预测方法。其中，单项预测方法包括灰色模型预测法、时间序列预测法、指数平滑法、BP神经网络预测法等，组合预测方法包括灰色马尔科夫链预测法、灰色神经网络预测法、灰色季节指数预测法等。事故预测指标包括绝对指标和相对指标。其中，绝对指标包括事故发生起数、死亡人数、经济损失等，相对指标包括百亿元产值死亡率、亿元 GDP 死亡率、十万从业人员死亡率等。通过查阅相关文献，发现学者们倾向于对事故的绝对指标进行预测，例如：杨灿生等[1]基于1994—2007年事故发生起数数据，将灰色 GM(1，1)模型和马尔科夫原理相结合，建立了事故预测模型，并在此基础上对2008—2009年的事故进行了预测，预测精度可达90%以上；陈春来[2]收集了12个建筑工程的安全损失影响指标数据，采用BP神经网络法，将安全教育、文明施工、现场安全设施、个人劳动防护作为输入，将安全损失作为输出，对建筑安全损失进行了预测，为施工现场的安全控制提供了指导；王书明等[3]采用时间序列ARIMA模型对我国2010—2014年的建筑安全事故死亡人数进行了预测。此外，有少数学者对事故的相对指标进行了预测，如王旭峰等[4]选取百万元产值死亡率作为预测指标，分别用非线性回归、指数平滑法、灰色预测法进行了单项预测，并建立了线性和非线性组合预测模型，发现基于BP神经网络的非线性组合预测模型的拟合和预测精度均好于其他预测模型。通过文献分析，发现多数学者侧重选取单一事故预测指标进行预测，而忽略了其他指标在反映建筑安全形势方面的优势，具有一定的片面性和局限性。

基于此，综合考虑事故预测相对指标和绝对指标在反映建筑业安全形势方面的优势，笔者以2010—2019年为预测时间段，选取绝对指标中的事故死亡人数和相对指标中的百亿元产值死亡率，借鉴相关文献[5]的做法，对两个指标先进行无量纲化处理后再进行加权平均，得到综合当量死亡率指标，分别采用灰色模型、指数平滑法进行预测，在此基础上，建立两者的最优加权组合预测模型，对比分析这3种预测模型的精度，并选取精度较高的模型对2020—2021年的建筑安全事故进行预测。

一、建筑安全事故预测模型解析

1.灰色模型

20世纪80年代，邓聚龙教授提出了灰色系统理论，该理论能够解决数据量较少，信息不完整且具有不确定性的问题。该理论中的灰色模型被学者广泛应用于医学、材料价格、交通事故、人口、粮食、建筑安全事故等方面的预测[6]。GM(1，1)模型可对数据少、序列不完整、可靠性低的时间序列进行预测，并且不需要考虑分布规则和趋势问题，是灰色模型中最普遍使用的，其建模原理如下：

设建筑安全事故原始数据序列为x(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}，则x(0)的一阶累加生成序列为x(1)={x(1)(1)，x(1)(2)，…，x(1)(n)}，在该一阶累加序列中，每一个数的统一计算式可表示为

①数据检验与处理。首先计算数列的级比值

(1)

y(0)(k)=x(0)(k)+c，k=1，2，…，n

(2)

则变换后序列的级比值为

(3)

此时，序列的级比值通过了检验，后续计算预测值时，需同时减去平移变换值c。

②建立灰色预测模型。累加序列x(1)关于时间t的白化微分方程为

(4)

式中：a、u是要求解的系数，分别为发展系数和灰色作用量。

解得

[a，u]T=(BTB)-1BTYn

(5)

其中，Yn为n-1维列向量，B为(n-1)×2矩阵，两者的表达式分别为

Yn=[x(0)(2)，x(0)(3)，…，x(0)(n)]T

于是得到式(4)的解为

(6)

③计算原始数据序列预测值。由于预测方程是由累加数据序列计算出的预测方程，因此，需要进行累减还原，即原始数据序列预测方程为

(7)

④灰色预测模型的精度检验。设残差为原始值和预测值的差值，则原始数据的残差组成的序列为

ε(0)=[ε(1)，ε(2)，…，ε(n)]=

(8)

表1 精度检验等级

2.指数平滑法

指数平滑法由布朗提出，布朗认为时间序列的态势具有稳定性或规则性，所以时间序列可被合理地顺势推延[7]。指数平滑法被不少学者[8-10]应用在各类事故的预测上。该方法适用于数据中短期预测，可分为一次平滑法、二次平滑法、三次平滑法甚至更高次数的平滑，一般三次平滑就能够满足预测要求。一次平滑法适用于时间序列比较平稳、没有显著变化趋势的预测，二次平滑法适用于有线性变化趋势的时间序列预测，三次平滑法适用于呈现非线性关系的时间序列预测。由于建筑安全事故呈现非线性关系，因此选用三次指数平滑法进行预测。三次指数平滑法的预测模型为：

(9)

(10)

(11)

(12)

(13)

(14)

(15)

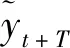
3.灰色模型和指数平滑法组合预测模型

组合预测模型能综合各单项预测模型的优势，有效提高预测精度。基于最优加权法的组合预测的建模步骤如下：

(16)

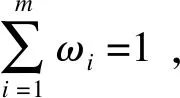
(17)

各预测模型可以构成拟合误差矩阵E，即

(18)

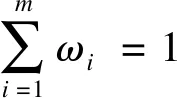
(19)

式中：Q为目标函数。将分量全为1的列向量记为R，W是由各单项预测模型的权重系数组成的m维列向量，即R=[1，1，…，1]T，W=[ω1，ω2，…，ωm]T，则式(19)可转化为

(20)

用拉格朗日乘数法求解最优权重向量为

(21)

(22)

4.模型评价指标

选取误差平方和(MSE)、平均相对误差(MRE)、平均绝对误差(MAE)作为模型精度的评价指标，其计算式分别为

(23)

(24)

(25)

二、建筑安全事故预测模型实例分析

以2010—2019年的建筑安全事故综合当量死亡率指标为例，分别用灰色模型、指数平滑法、灰色模型和指数平滑法组合预测模型进行预测，并计算相应的评价指标，然后选取精度较高的模型对2020—2021年的综合当量死亡率指标进行预测，从而判断未来建筑业的安全形势。

1.预测指标数据的收集

综合当量死亡率指标由事故死亡人数和百亿元产值死亡率分别经无量纲化处理后再加权平均组成，计算式为

(26)

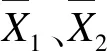
表2 预测指标数据统计

2.灰色GM(1，1)模型预测

经计算，原始数据没有通过级比检验，需对原数据进行平移转换，即在原始值基础上加入平移转换值1.00，最终经平移转换后的数据级比检验值均在区间[0.834，1.199]内，意味着数据适合进行GM(1，1)模型构建。由式(5)可计算出，a=0.004 2，u=1.999 6，将a、u带入式(6)中，可计算出累加数列的预测值方程为

由式(7)计算出平移后的原始预测值，再分别减去平移转换值1.00，即得到原始值的预测值。对模型进行精度检验，后验差比值C=0.389，小误差概率P=0.80，由表1可知模型精度等级为合格。具体计算结果如表3所示。

3.指数平滑法预测

首先估算平滑初始值，由于本实例选取了10 年的数据，因此取前两年数据的平均值作为初始值，即

经试算，平滑系数α=0.4，由式(9)～(15)即可求出原始数据的预测值。计算结果如表3所示。

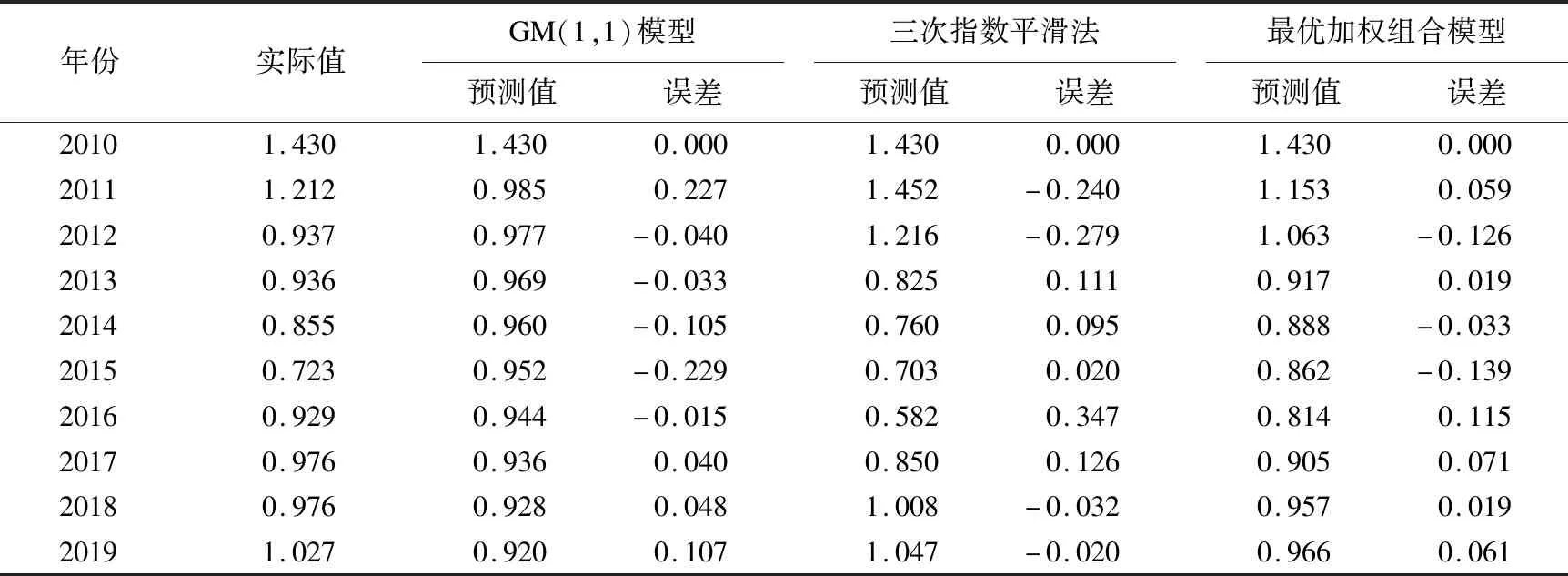
表3 不同模型的预测结果

4.灰色模型和指数平滑法组合预测

(27)

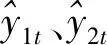
5.预测模型的评价指标

根据式(23)、(24)、(25)，可求出3种预测模型的评价指标。

灰色GM(1，1)预测模型的评价指标为

MSE=0.133 262，MRE=0.091 528，MAE=0.084 4。

三次指数平滑法预测模型的评价指标为

MSE=0.294 896，MRE=0.130 802，MAE=0.127 0。

最优加权组合模型的评价指标为

MSE=0.062 476，MRE=0.070 970，MAE=0.064 2。

6.实验结果及分析

通过对比分析3种预测模型的评价指标，可以看出：在单项预测模型中，灰色模型的评价指标在误差平方和、平均相对误差、平均绝对误差3个方面均优于三次指数平滑法，说明灰色模型预测精度较高；最优加权组合模型在3个评价指标方面均优于灰色预测模型、三次平滑法，说明对单项预测模型采用最优加权后，预测模型的精度得到了提高。运用该组合模型对2020—2021年的综合当量死亡率进行预测，结果分别为0.981，1.007，可见建筑业安全生产形势依然严峻，需采取有效措施预防和控制事故的发生。

三、结 语

安全问题是建筑业关注的热点问题，建筑安全事故的有效预测能够加深管理人员对于安全形势的认识，从而采取有效措施预防和控制事故的发生，提高施工现场的安全管理水平。通过建立单项预测模型和组合预测模型，分别预测2010—2019年的综合当量死亡率，并比较分析3种模型的误差平方和、平均相对误差、平均绝对误差3项指标，发现组合模型的预测精度高于两种单项预测模型，能够有效降低预测误差，为建筑安全事故预防提供决策参考。