基于线性调频信号二次相位变换的主动声呐目标速度估计

顾怡鸣，宫在晓，李整林

(1. 中国科学院声学研究所声场声信息国家重点实验室，北京 100190；2. 中国科学院大学，北京 100190)

0 引 言

线性调频(Linear Frequency Modulation, LFM)是主动声呐常用的探测信号，通过分析 LFM 信号目标回波可估计目标与探测平台的相对速度。传统的LFM测速方法主要有多普勒频移补偿法和组合脉冲法。多普勒频移补偿法利用长脉宽 LFM 信号的多普勒敏感性，对探测信号进行多普勒频移搜索来估计相对速度[1]。组合脉冲法利用LFM信号模糊函数的时延-多普勒耦合性，通过正负调频信号匹配滤波峰值的时延差估计速度，也被扩展应用于双曲调频信号[2]。但主动声呐的发射占空比通常较小，组合脉冲增加了信号的发射周期。

分数阶傅里叶变换(Fractional Fourier Transform, FrFT)是一种时频旋转变换，近年来已经被广泛用于 LFM 信号的检测和参数估计[3-13]。文献[14]首先将 FrFT应用于主动声呐回波检测，并利用海上实验数据证明了 FrFT在混响背景下可以获得比匹配滤波器更高的信噪比和速度估计精度。但FrFT较高的计算复杂度限制了其实际应用，针对该问题，学者们提出了一些快速 FrFT算法[15-21]。采样型算法对时间和频率进行尺度归一化，可以借助快速傅里叶变换(FFT)算法极大地降低计算量[15-16]；特征向量分解型算法[12-13]通过设计离散傅里叶变换矩阵求解对应的特征向量；文献[21]中利用莫比乌斯反演公式证明了分数阶傅里叶级数的存在，并以此为基础提出了低复杂度的离散FrFT算法。FrFT方法检测 LFM 信号主要利用了其解调频的性质，舍弃一些冗余的性质，对变换形式进行简化以降低计算量，例如二次相位变换[22-24](Quadratic Phase Transform, QPT)或简明分数阶傅里叶变换[7-8]，以及具有高次变换核的多项式时频变换[25-26]。

现有的 FrFT估计速度方法需要对变换参数进行搜索，在自主水下机器人(Autonomous Underwater Vehicle, AUV)等计算力有限的平台难以实时处理。本文针对该问题提出了一种基于二次相位变换的线性调频信号速度估计方法。QPT参数失配时能量无法聚焦，幅度谱存在一定展宽。本文推导了 QPT参数与信号参数失配时变换域幅度谱的解析解，分析了二次相位变换幅度谱展宽与多普勒频移之间的关系，提出了利用单次QPT后幅度谱宽度的速度估计方法。基于单个线性调频信号进行QPT后幅度谱的展宽信息实现了目标相对速度估计，避免了对变换参数的扫描，减少了一个维度的计算量。针对单次QPT结果无法确定速度符号的问题，提出了对称参数QPT符号判断方法。通过数值仿真验证了方法的有效性，并与 FrFT参数扫描方法进行了对比。

1 FrFT测速方法

FrFT的变换参数cotα与信号的调频斜率k匹配时，变换核中的 ( t2/2)cotα项对信号实现解调频，变换结果的幅度取得最大值。文献[14]依据该性质给出了通过扫描 FrFT变换参数搜索最大峰值的测速方法。以长度为20 s、频带400～500 Hz的LFM信号为例，根据式(5)得到FrFT对LFM信号u-多普勒模糊(见图1)。由图1可以看出，当变换参数与信号速度匹配时变换结果的幅度取得最大值。FrFT测速方法的原理是在变换域-多普勒平面内搜索最大值，找到最大值对应的变换参数，进而通过变换参数与多普勒频移之间的关系得到目标相对速度的估计值。

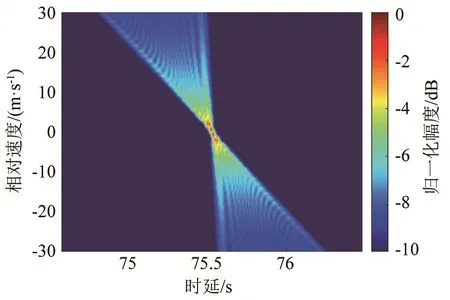
图1 FrFT对LFM信号的u-多普勒模糊图Fig.1 Schematic diagram of the u-Doppler ambiguity of FrFT for LFM signal

2 QPT速度估计方法

2.1 参数失配时LFM信号的QPT

二次相位变换可以看作是 FrFT的简化，信号x(t)的QPT定义为[25]

其中，u和κ是变换参数。当变换参数和线性调频信号的调频斜率k匹配，即k =κ 时，信号能量会在变换域聚集为峰值，此类情况已经在现有文献中广泛讨论；当变换参数与信号参数失配时k≠κ ，信号的能量在变换域表现为一定展宽，已有文献尚未发现有关变换参数与信号参数失配时特征的研究。以下给出变换参数与 LFM 信号调频斜率不匹配情况下变换结果的解析解。

多普勒频移后的回波信号二次相位变换可表示为

变换后信号的幅度谱由两种形式的 Fresnel积分(如图2所示)决定，式(10)对应的幅度谱大部分区域为零，如图3所示，能量集中在一定的宽度，定义幅度谱宽度Bα为幅度谱峰值-3 dB对应的u域宽度，能量集中的范围的宽度为

图2 宗量为x的Fresnel积分Fig.2 Fresnel integral with argument x

图3 多普勒频移后的回波信号QPT的幅度谱示意图Fig.3 QPT amplitude spectrum of the echo with Doppler frequency shift

2.2 单次QPT速度估计方法

以上推导表明，参数失配时LFM信号QPT的幅度谱宽度与信号多普勒频移存在确定关系，利用该特征可估计目标相对速度。若变换参数为原始信号参数时κ= k，LFM信号QPT的幅度谱的宽度为

式中：c为声速；k和T为LFM信号的调频斜率和脉冲宽度。只需要通过估计幅度谱宽度Bk即可得到相对速度。QPT幅度谱的宽度信息可通过阈值检测获取，即：

其中：d为检测门限，根据阈值检测幅度谱的前后沿u0和u1可估计幅度谱宽度的估计值目标静止时QPT幅度谱为sinc函数，幅度谱宽度为。需要注意的是，式(10)并不是完美的矩形窗函数，检测门限较高时估计的宽度会偏小，需要通过修正系数进行补偿。

根据 QPT幅度谱的宽度可以估计相对速度 v的大小，相对速度的符号则可以根据幅度谱前沿与的关系来确定：

假设 LFM 信号长度为 20 s，频带 400～500 Hz，对相对速度为 0和 30 m·s-1的信号进行QPT后得到的幅度谱分别如图4(a)和图4(b)所示，可以看出，当相对速度为0时，信号能量在变换域聚焦，信号QPT幅度谱几乎没有展宽。相对速度为30 m·s-1时，信号QPT幅度谱展宽明显，并且与式(11)理论分析的宽度一致。图4(c)为QPT对LFM信号u-多普勒模糊，可以看出，随着相对速度的增加，QPT幅度谱逐渐展宽。同时，当相对速度为正时，幅度谱分布位于f0- kτ0右侧，相对速度为负时位于f0- kτ0左侧。由于信号的能量一定，QPT幅度谱的幅度随展宽而降低。经过阈值检测后的宽度图像如图4(d)所示，根据宽度可以进一步估计目标相对速度。需要注意，单次QPT方法依赖式(14)判定速度的正负，实际应用中不能准确获取时延τ0，因此单次 QPT提供的信息在判断速度的正负方面存在缺陷。

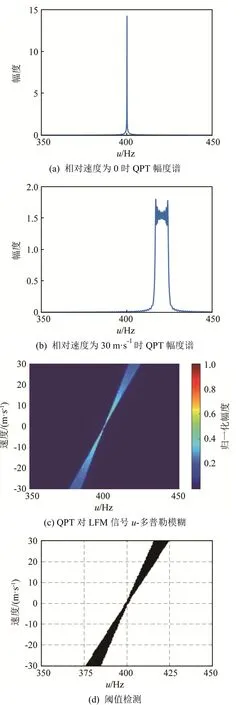
图4 单次QPT的速度估计方法Fig.4 Velocity estimation method with single QPT

2.3 对称参数QPT速度符号判断方法

单次 QPT谱宽度仅提供了相对速度的大小信息，不能确定相对速度的符号，这里给出对称参数QPT速度符号判断方法。图 5为符号判断方法的示意图，给定一个初始宽度B0，若信号不存在多普勒频移时，B0对应的两组变换参数分别为分别对回波信号进行变换参数为κ+和κ-的 QPT，分别可以得到两组变换的幅度谱宽度Bκ+和Bκ-，两次对称参数 QPT幅度谱宽度为

图5 对称参数QPT速度符号判断示意图Fig.5 Schematic diagram of speed symbol judgment with symmetrical parameter QPT

由式(15)可以看出，当信号相对速度为正时，伸缩因子η＞ 0，Bκ+＜ Bκ-；当信号相对速度为负时，伸缩因子η＜0，Bκ+＜ Bκ-。通过对比两次对称参数QPT幅度谱宽度可判断相对速度的符号。

3 仿真实验与性能分析

本节通过数值仿真实验验证 QPT速度估计方法的有效性，并将QPT方法与FrFT参数扫描方法的性能进行对比。仿真环境为无限空间，海水声速为 1 500 m·s-1。仿真实验的部署如图 6(a)所示，蓝圈静止位于坐标原点(0, 0)的收发合置的主动声呐平台，黑圈代表目标起始位置(-10 km, 5 km)，虚线代表目标自东向西以速度 200 m·s-1匀速运动的航线。根据目标运动速度和相对平台的方位可以得到目标与平台的相对速度如图6(b)所示，正速度表示目标接近平台。探测信号为长度 20 s、频带 400～500 Hz的LFM信号，信号发射周期为60 s。在整个20 km的运动距离内，总计发射16个脉冲。

图6 仿真实验部署Fig.6 Deployment of simulation experiment

仿真接收信号的采样频率为5 000 Hz，假设背景噪声为高斯白噪声，回波信号频带内的信噪比为20 dB。仿真回波信号直接经过QPT后的幅度谱如图7(a)所示，回波QPT后幅度谱能量集中的位置与回波的时延有关。为了更加直观地表现相对速度对 QPT幅度谱的影响，将 u坐标变换为u′坐标，结果如图 7(b)所示。对比真实相对速度(图 6(b))可以观察到 QPT幅度谱宽度与相对速度大小的对应关系，设置检测门限为，进行宽度检测并依据式(12)的函数关系即可估计目标的相对速度。图8为对称参数QPT得到的幅度谱宽度检测结果，其中蓝线和红线分别对应正参数和负参数变换对应的幅度谱宽度，通过对比两者之间的大小可以判断速度的正负。

图7 仿真数据QPT谱宽度估计Fig.7 Estimation of the of QPT spectrum width of simulation data

图8 对称参数QPT幅度谱宽度估计结果Fig.8 Estimation of the amplitude spectrum width by using QPT of symmetric parameters

在实际应用中，FrFT测速方法不需要对0～π所有的变换参数进行搜索，通过速度和变换参数的关系限定参数扫描的范围可以降低计算量。速度扫描范围确定后，计算量与扫描的分辨率相关，扫描分辨率也直接决定了 FrFT方法的速度估计精度。仿真中，FrFT方法的速度扫描范围限定在-30～30 m·s-1范围内，扫描间隔分别采用3、1和0.3 m·s-1，对应的FrFT点数Nα分别为10、60和100点。分别利用 FrFT和 QPT两种方法对相对速度进行估计，得到速度误差如图9所示。由图9可以看出，FrFT方法的速度估计精度主要与参数扫描的分辨率有关，仿真数据单次QPT方法的速度估计精度基本可以保持在1 m·s-1以内，与60点的FrFT方法精度相当。

图9 FrFT参数扫描方法与单次QPT方法速度估计误差对比Fig.9 Comparison of velocity estimation error between FRFT parameter scanning method and QPT method

FrFT类算法的计算复杂度分析在许多文献中已有讨论[7-8,15,26]，尽管QPT简化了变换核，但计算复杂度仍与 FrFT的量级相当。忽略计算复杂度的低阶项，两种变换基于 FFT的快速算法计算复杂度量级均为O(NlgN)，其中N表示单次处理的时域数据点数。远程主动探测回波处理的时间窗较长，处理点数的增加使算法的时间复杂度急剧上升。以第2节仿真实验中采用的参数(窗长度40 s，采样点数20 000点)为例，评估不同参数扫描量的计算量，结果如图10所示，Nα=1对应的虚线表示单次QPT的计算量。如果只估计相对速度大小，QPT计算量仅为精度相当的FrFT方法的1/60；增加判断相对速度符号，则计算量为FrFT方法的1/30。

图10 不同参数扫描量的计算量估计Fig.10 The computational costs of different scanning parameters

参数失配时能量在变换域并非聚焦于一点，因此 QPT方法的抗噪声性能差于 FrFT参数扫描方法。假设回波信号的带内信噪比为 20 dB，不同相对速度回波信号的QPT幅度谱波形如图11所示，相对速度为0时，信号能量完全聚焦，背景起伏很低，随着相对速度提高，背景起伏逐渐升高。定义峰值信噪比为输出信噪比，通过 20次蒙特卡洛仿真估计QPT和FrFT两种方法的输出信噪比随相对速度的变化，结果如图12所示，蓝线和红线分别表示QPT方法和FrFT方法的输出信噪比。可以看出，QPT方法的输出信噪比在相对速度为0时输出信噪比与FrFT方法相同，随着目标相对速度提高，信号能量在变换域逐渐分散，输出信噪比逐渐降低。上述数值分析表明，QPT方法的抗噪声性能比FrFT方法差，该方法计算效率提高的代价是输出信噪比的降低。虽然经典的 FFT谱分析方法通过分析信号频偏也可获得目标速度，但主动声呐接收的目标回波信号通常信噪比很低，FFT完全无法聚焦信号的能量，输出信噪比远低于以上两种方法。

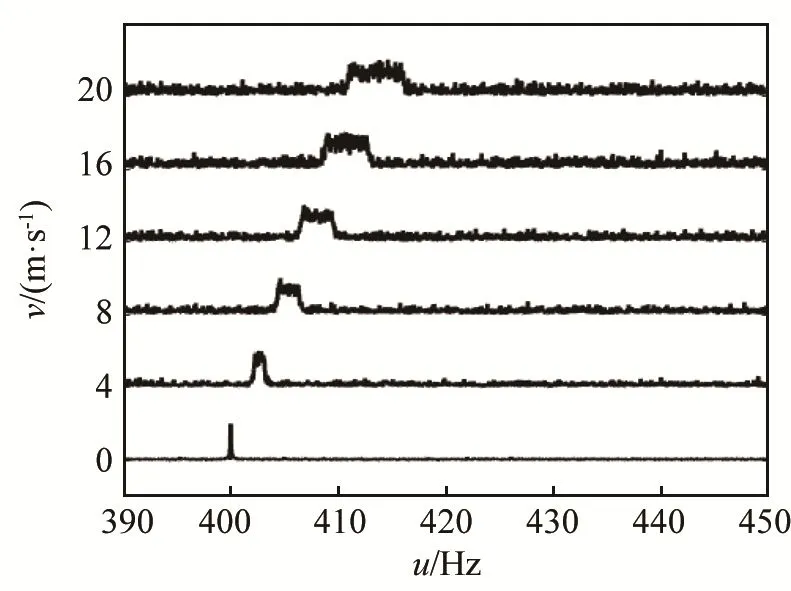
图11 不同相对速度QPT幅度谱的波形Fig.11 Waveforms of QPT spectrums corresponding to different relative velocities

图12 QPT方法和FrFT方法的输出信噪比对比Fig.12 Comparison of output signal to noise ratio between QPT method and FrFT method

4 结 论

本文提出了一种基于二次相位变换的主动声呐线性调频信号的速度估计方法，通过减少变换次数降低了 FrFT类算法速度估计的计算量。单次QPT速度估计方法利用LFM变换后幅度谱宽度与信号多普勒频移的关系对速度进行估计，速度符号的判断依赖准确的到达时刻。针对实际情况下难以准确估计时延的问题，提出了对称参数QPT速度符号判断方法，通过对比对称参数变换的幅度谱宽度判断速度符号。由于不需要对变换参数进行搜索，相较于 FrFT参数扫描的方法，所提速度估计方法可以降低一个维度的计算量。仿真实验结果表明，该方法的速度估计精度可以达到1 m·s-1，如果只估计相对速度大小，计算量仅为精度相当的FrFT参数扫描方法的1/60。但该方法计算效率提高的代价是输出信噪比的降低，在实际应用中需要进行权衡。考虑到复杂海洋环境条件下主动声呐接收回波信号存在畸变，本文的方法还有待复杂信道下真实主动声呐实验数据的验证。